新型装配墙式质量调谐阻尼器抗震性能研究

尹 航， 刘书贤， 路沙沙， 张贵军， 聂 伟， 李晓峰， 徐 红

(辽宁工程技术大学 土木工程学院，辽宁 阜新 123000)

调谐质量阻尼器(tuned mass damper，TMD)自20世纪50年代诞生以来，经过半个多世纪的发展，理论体系逐渐成熟，TMD主要由弹簧、质量块和阻尼器组成，通常调谐到主系统固有频率工作。近年来全球已有许多成功的结构实施案例，纽约市的花旗集团中心、横滨的横滨地标大厦、迪拜的帆船酒店、纽约市的特朗普世界大厦、台北的台北 101 和柏林的电视塔都是配备了TMD的建筑[1]。现阶段阻尼器类型有液体调谐质量阻尼器(liquid tuned mass damper, LTMD)[2]、涡流阻尼器[3]、摆式调谐质量阻尼器(pendulum tuned mass damper， PTMD)[4-5]，其基本减震原理是当结构遭受外激励时，TMD产生与主结构相反的惯性力，抵消部分地震作用[6]，减小外激励对结构的影响，从而实现减震控制效果。鲁正等[7]应用液体调谐和颗粒碰撞协同减振的原理对一种组合型质量阻尼器开展振动台试验，发现组合型质量阻尼器在全频带内均有减震效果且低频内减震效果更佳。刘金栓[8]针对一种以单纯改变质量来实现频率可调的被动调谐质量阻尼器，通过振动台模型试验研究其可行性及振动控制效果，并利用MATLAB软件对试验所测得的结果进行分析。袁康等[9]设计了不同阻尼器钢片厚度(频率比)，不同质量块布置(质量比)的填充墙MTMD减震结构，进行了不同地震输入水平下的振动台试验和动力时程分析。表明对于第一振型为主的多层结构，质量块布置数量对减震效果影响不明显，可考虑仅在顶层设置TMD质量块。赵祥等[10]提出了一种新型变阻尼式TMD，并将该阻尼器安装在两层单跨的钢框架模型结构上。通过对比无控状态、传统 TMD 控制状态和变阻尼式 TMD 控制状态下钢框架结构的动力响应，分析了变阻尼式 TMD在不同激励下的减震控制效果。卢俊辉等[11]设计了两边均由U型垫片连接的填充墙作为TMD调节质量块，得出了填充墙TMD结构中TMD连接参数的计算方法。并通过振动台试验分析其减振效果，但设计的TMD装拆不便，参数不能灵活调整，在结构损伤累积中会发生失谐现象。

无论何种类型TMD，其本质是依靠较大质量块实现调谐，附加质量势必会大幅增加造价成本，占用有限的空间资源，而如何充分利用现有建筑的各组成部分的质量，实现减震控制目标，同样是一个具有广阔研究意义的课题。有关TMD的研究大多数聚焦在TMD的位置、数量、参数优化等方面的理论分析，忽略了对现有建筑的各组成部分的质量利用来改进提高其工作性能，并且针对该研究方向的TMD减震控制振动台试验有所欠缺。

本文设计了一种装配墙式减震TMD，将传统墙体设置成具有TMD减震特性的墙式TMD，该墙体可充分利用墙体现有质量，节约使用空间，装配式的构造可实现TMD配件的及时更换。为了检验墙体抗震性能，建立了TMD结构耦合运动方程，对无控结构和墙式TMD结构的传递函数进行了推导，并通过振动台试验对比无控结构和墙式TMD受控结构动力响应，验证其减震效果。

1 墙式质量调谐阻尼器的设计

在相关研究中所采用的TMD减震结构，需要将特定的调谐质量块与主结构通过阻尼器连接形成TMD系统，结构构造较为复杂，不便于装拆，且会增加结构造价。为此，本文自主研发设计了一种新型装配墙式TMD减震结构。墙式TMD减震结构的主要特点是将传统建筑结构中不参与结构受力的墙体与主体承重结构分离，二者通过阻尼器与抗压件连接，如图1 所示。图1由弹簧、高强螺栓、螺母、复位拉杆、摩擦橡胶、调压螺栓、预埋U型钢片、挡板、质量块、铁框、滚轮组组成。整体构造中，挡板与预埋在结构中的钢片通过螺栓连接，墙体外包铁框上焊有螺母与墙体共同组成质量块体系，并与复位拉杆一起由高强螺栓固定，复位拉杆末端套有摩擦橡胶和弹簧。当外激励发生，墙式TMD在惯性力作用下随着结构左右平动，弹簧为结构提供恢复力，使结构具有自复位功能，摩擦橡胶与调压螺栓相连，通过拧动调压螺栓可调节摩擦橡胶与复位拉杆的正摩擦力，为结构提供所需阻尼，装拆时只需要拧动高强螺栓便可使复位拉杆与质量块体系分离，随意更换结构配件。其中，主结构为主要的竖向和水平受力构件，墙式TMD减震结构不仅具有填充建筑物的功能，同时作为 TMD系统中的质量块，与消能减振装置有机结合起来，形成 TMD 系统以耗散地震能量，为了防止激励发生时TMD质量块出平面破坏，在隔震支座两侧安置平面限位挡板，具体构造可参考专利[12]。

1.弹簧；2.螺母；3.高强螺栓； 4.复位拉杆；5.摩擦橡胶；6.调压螺；7.预埋U型钢片；8.挡板；9.滚轮组；10.质量块；11.铁框。图1 墙式减震TMD示意图Fig.1 Schematic diagram of wall-mounted shock absorption TMD

2 结构-TMD系统数值模型

袁康等对于填充墙MTMD减震结构试验表明，对于第一振型为主的多层结构，质量块布置数量对减震效果影响不明显，可考虑仅在顶层设置TMD质量块。基于此，本文墙式TMD减震结构仅于顶层对称布置，墙式TMD结构的数学模型如图2所示，根据牛顿力学原理可得到式(1)，各矩阵为

图2 墙式TMD 的数学模型Fig.2 Mathematical model of wall-tuned mass damper

(1)

矩阵C

矩阵K

式中：X为结构-TMD系统的位移向量，xi为第i层楼板对地面的相对位移(i=1, 2, …,N)，xt为阻尼器对地面的相对位移；xg为由于地震引起的地面位移；m*为加速度质量矩阵;M,C,K均为包含了墙式TMD参数的N+1维矩阵矩阵。其中：M为结构-TMD系统的质量矩阵，mi为第i层楼板的质量(i=1, 2, …,N)，mt为阻尼器的质量；C为结构-TMD系统的阻尼矩阵，ci为第i层楼板的阻尼(i=1, 2, …,N)，采用Rayleigh阻尼假定，即ci=α1mi+α2ki，其中α1，α2为阻尼系数与结构的振动特性有关，ct为阻尼器的阻尼；K为结构-TMD系统的刚度矩阵，ki为第i层楼的刚度(i=1, 2,…,N),kt为阻尼器的刚度。

3 传递函数

(2)

式中：HxN(ω) 为第N层结构传递函数；Hxt(ω)为墙式TMD传递函数，通常以结构顶部传递函数为主要控制对象。

为了获得更准确的墙式TMD参数，使用Den Hartog[13]经典阻尼参数计算式(3)对本文墙式TMD系统进行参数优化，其中αopt为频率比，ξopt为阻尼比、μ为质量比、ft和fs分别为TMD结构自振频率和主结构自振频率。

(3)

根据上述最优参数计算方式，使用MATLAB计算并绘制了不同TMD质量比下的主结构传递函数图，如图3所示，可以看出墙式减震TMD显著降低了主结构传递函数峰值，随着TMD结构质量比的增大，调谐频带逐渐加宽，传递函数峰值逐渐减小，但减小程度逐渐放缓，而安装减震TMD所需的最优参数(刚度、阻尼)均逐渐增加。Farshidianfar等[14]表明TMD质量比一般为建筑总质量5%～10%，权衡试验条件，本文质量比取为6%，其传递函数峰值减震幅值达60.5%。

具体计算过程如下，将质量比μ=6%，代入Den Hartog式 (3)，计算αopt，ξopt分别为0.943和0.145，将fs，mt回代式(3)进一步计算Kt和Ct，最终可得Kt=17.3 N/mm，Ct=101 N·s/m，运行得到墙式TMD最优参数如表1所示，本文基于此方式对墙式TMD进行参数设计。

表1 结构优化结果Tab.1 Structural optimization results

图3 传递函数对比图Fig.3 Transfer function comparison chart

4 墙式TMD框架结构振动台试验

为了验证墙式TMD减震效果，对受控体系进行了振动台测试。研究中使用的振动台设备由3 m×3 m的平台组成，额定负载10 t，可双向水平运动频率范围：0～50 Hz，满载下峰值加速度为1.5g；加速度计采用东华测试生产的IEPE压电式加速度传感器。轴向灵敏度(23±5 ℃)107.6 mV/m/s2，量程±5g，最大横向灵敏度<5%。

试验对一栋单跨三层框架结构框架模型进行1/10缩尺振动台试验，结构尺寸如图4所示，原型结构层高为3 m，总高为9 m，混凝土强度为C30；柱子尺寸为450 mm×450 mm；框架梁截面尺寸为300 mm×450 mm；框架柱网为6 m×6 m；楼板板厚120 mm；加速度计用字母“A”表示。结构上布置的6处，分别位于台面中心(A1)、垂直于振动方向每层楼板边侧(A2、A3、A4)、墙式TMD中心(A5、A6)，A6位于结构另一侧墙式TMD上，因此，图4(a)中未画出，墙式TMD框架结构如图5所示，基础使用留有螺孔的10 mm厚钢板通过M20高强螺栓固定在振动台台面。试验各物理量的相似关系采用量纲分析法确定，以Sl，Sa和SE为基本可控相似常数，为达到响应相似比要求，其余物理量相似关系可由量纲分析推算得出[15-16]，模型采用微粒混凝土与镀锌铁丝构建，根据计算结果，模型结构属欠人工质量模型，额外增加铅块配重[17-18]，最终模型相似比如表2所示。

图4 框架模型平面尺寸(mm)Fig.4 The plane size of the frame model (mm)

表2 振动台试验相似常数Tab.2 Similar constant of shaking table test

图5 墙式TMD框架结构Fig.5 Wall-tuned mass damper frame structure

5 试验加载工况

试验对比分析了，无控框架结构和墙式TMD框架结构的减震效果，每种工况开始前使用0.05g峰值的高斯白噪声进行扫频，通过白噪声扫频采集模型自振频率，为了探讨输入地震动特性对试验结果的影响，选择三条频谱成分差异较大、具有代表性的地震波作为台面输入地震动，分别是Kobe波、Taft波和Northridge地震波，三条输入地震波的时程图及响应谱图，如图6所示，依据GB 50011—2010《建筑抗震设计规范》[19]对地震波进行设计，地震波峰值从0.1g逐级增加至0.6g，试验中对每条地震波的峰值加速度及时间间隔均根据相似关系进行调整。

图6 地震波时程曲线及反应谱Fig.6 Seismic wave time history curve and response spectrum

6 试验结果与分析

为获取结构的动力特性，在试验开始前通过输入加速度峰值为0.05g的白噪声测试，结构模型在无控、墙式TMD受控下结构的自振频率分别为8.24 Hz，7.84 Hz。由此可知，安装减震装置后，结构的自振频率较无控状态有所降低，使得结构的周期有一定的延长；减震摇摆墙TMD质量取为6%，墙式TMD参数根据表1得到，单侧墙体Kt=8.65 N/mm，Ct=50.5 N·s/m。

6.1 减震工作机理验证

如引言所述，墙式TMD体系减震原理是TMD质量块在发生外激励情况时，产生相反惯性力抵消结构系统的运动，对于这种减震方式的实现，需保证减震子结构的自振频率与受控主结构相近且运动反向相反，或减震子结构反应延迟不同步。本文通过对减震框架结构(主结构)顶层和墙式减震TMD(子结构)的位移时程曲线进行对比，以验证减震结构的工作机理。当输入地震加速度峰值为0.6g时，框架主结构和减震TMD子结构的位移时程曲线，如图7所示。

从图7中不难发现，墙式减震TMD在抵抗振动过程中整体呈现平动特性，墙式减震TMD与主结构的动力反应时程曲线形状相似，但存在一定的相位差，墙式减震TMD位移滞后于主体框架，某些时间节点甚至方向相反，表明结构在振动过程中减震结构与受控结构间发生了相对运动，这种特性体现了模型被动减震的特点。此外，从图中动力反应时程中可见，墙式减震TMD的位移大于主体结构，其原因在于墙式减震TMD与主体结构非刚性连接，而是由减震弹簧连接，在运动过程中的惯性作用增大了自身动力响应，但由于主子动力响应不同步，使得其惯性力反作用于主体框架上，实现模态传递减震功效。

图7 体框架与减震TMD墙位移时程曲线Fig.7 Displacement time history curve of the main frame and the shock-absorbing TMD wall

6.2 加速度响应分析

为了检测墙式减震TMD减震性能，对框架模型结构分别进行了Kobe 波、Taft波和North波作用下的振动台试验，各工况顶层加速度时程对比如图8所示。图8中可以明显看出，墙式减震TMD在整个地震激励过程中对结构加速度均产生了振动抑制效果。顶层加速度响应最大值(peak ground acceleration PGA)及减震率在表3给出，结合表3可知，Kobe波作用下的结构响应与Taft波作用下的结构响应相似且均较大，这可能是由于这两种地震波激励频率与主结构自振频率相近；Kobe波作用下，墙式减震TMD对结构楼层平均减震率为20.32%，Taft波和North波作用下分别为11.7%和12.6%，顶层为减震效果最明显楼层，最大减震率分别为29.7%，23.6%，26.9%，该结果表明地震波的频谱成分很大程度上影响墙式减震TMD的减震效果，一般来说越接近结构自振频率，结构动力响应越大。不同加速度峰值激励下，各楼层加速度峰值对比如图9所示，不难看出墙式减震TMD在不同的地震激励峰值情况下，各楼层均取得了较好的减震效果，顶层减震效果优于其他楼层，且外激励越大这种减震效果越明显。

图8 顶层加速度时程响应Fig.8 Time-history response of top layer acceleration

图9 楼层加速度峰值对比图Fig.9 Comparison of peak floor acceleration

6.3 频谱分析

对从测试中收集到的顶层加速度进行了快速傅里叶变换(fast Fourier transform,FFT)，以了解受控和无控结构之间的动态特性差异，如图10所示。在三种不同地震激励下傅里叶变化峰值均出现在结构自振频率(8.24 Hz)附近，分别为8.99 Hz，8.50 Hz，7.88 Hz，低频分量的傅立叶频谱被放大，高频分量均被衰减。安装了墙式减震TMD的受控结构，其傅里叶峰值所处频率均小于无控结构，这可能是由于装有墙式减震TMD的受控结构的自振频率较无控结构有所降低，延长了结构振动周期。安装了墙式减震TMD的受控结构，在三种激励下均在一定程度上降低了傅里叶峰值，其FFT峰值分别减小了36.9%，36.8%，35.3%，因此，由上述可以推断，墙式减震TMD具有明显的减震与频率调谐作用。

图10 顶层幅频响应曲线Fig.10 The amplitude-frequency response curve of the top layer

表3 加速度减震率对比表Tab.3 Comparison table of acceleration damping rate

6.4 位移响应分析

为了更好地分析墙式减震TMD的减震性能，对 Kobe 波、Taft 波和North波作用下受控结构各层的位移最大值进行对比，图11可看出在三种地震波作用下，结构顶层的位移值均大于结构底层；与加速度响应相似，Kobe 波与Taft波作用下的位移最大值均大于North波作用下的位移最大值，这主要是由于 Kobe 波的与Taft波卓越周期与结构的自振周期较为接近，因而结构的反应较North波作用下结构响应激烈。各工况最大减震率对比如表4所示，结构在加入装配式墙式减震TMD装置后，其位移响应显著降低，且随着加速度峰值的增加，位移减震效果越发明显。由于调谐类阻尼器以控制结构的第一振型为主，因此，墙式减震TMD安置于结构的顶层，可以看出其对结构顶层的位移控制效果明显优于结构底层的控制效果；对比位移与加速度减震效果，整体来说该墙式减震TMD对位移的控制效果好于对加速度控制效果。

值得注意的是，墙式减震TMD在加速度峰值为0.6g的Taft波作用时，加速度和位移减小率分为23.6%和27.8%，为三种地震波中最低，根据Den Hartog的研究表明，外激励主频率成分与结构自振频率越接近减震效果越明显，而Taft波相较于其余两种地震激励其频率成分更接近结构自振频率，比较图11中Taft波引起的结构位移，分析造成此现象的原因可能是由于墙式减震TMD位移过大与主结构预埋铁皮发生碰撞，导致墙式减震TMD的调频作用受到影响。在后续的试验中增大了墙式TMD位移极限，有效增大了墙式减震TMD在各地震激励下的减震能力。

图11 楼层位移峰值对比图Fig.11 Comparison of peak displacement of floors

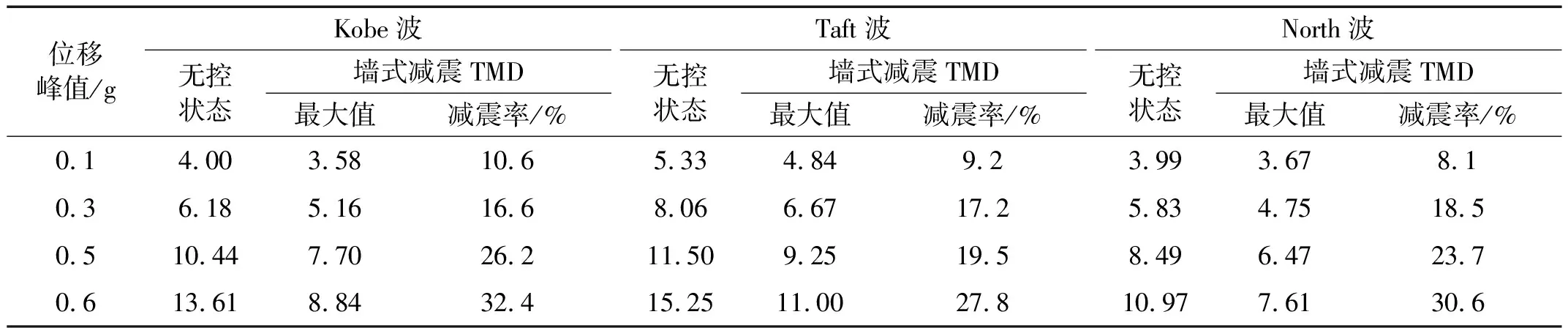
表4 位移减震率对比表Tab.4 Comparison table of displacement damping rate

7 结 论

本文在TMD减震装置的研究上，设计一种新型装配墙式减震TMD装置。将装置安装在三层单跨的混凝土框架模型结构中，在三种不同地震波激励下进行振动台试验研究，得出以下结论：

(1)通过对比无控结构和受控结构的传递函数，结果表明基于Den Hartog公式优化的TMD安装后，受控结构传递函数幅值明显小于无控结构。

(2)随着TMD结构质量比的增大，调谐频带逐渐加宽，传递函数峰值逐渐减小，但减小程度逐渐放缓，而安装减震TMD所需的最优参数(刚度、阻尼)均逐渐增加，因此，应结合工况选取合适的质量比，避免材料的浪费。

(3)白噪声试验结表明装有新型装配墙式减震TMD的结构自振频率较无控结构有所降低，并延长了结构振动周期。

(4)振动台试验结果表明，按最优参数条件下设置的墙式减震TMD，明显降低了受控结构的动力响应，且随着地震动峰值的增加，减震装置的控制效果越发显著，表明了装配式构造的合理性和参数优化设计的有效性。

(5)所设计的墙式TMD减震装置，可充分利用墙体质量，实现减震控制。并且相对于传统TMD，本文设计的墙式TMD具有节省空间、便于装拆、配件可更换的优点，具有装配式建筑的特点，响应我国绿色建筑的号召，具有广阔的应用前景。

在后续的应用中，应注意墙式TMD位移极限问题，防止墙体与结构发生碰撞，影响减震效果；在后续的研究中，可针对材料非线性问题，进行变阻尼墙式TMD减震装置的设置，进一步提高减震效果。