温度与地震共同作用下溢洪道结构优化研究

于宪政，陈健云，徐 强，李 静，刘鹏飞

(大连理工大学 建设工程学部 水利工程学院工程抗震研究所， 辽宁 大连 116024)

当前，我国对水利水电工程的建设日益重视，水电站修建带来了很多经济和社会效益，其运行期的安全问题也被人们重点关注。溢洪道结构是水电站重要的附属结构，往往承担着泄洪的重任，溢洪道结构由于体型较狭长，在运行期间的温度应力往往不能忽视[1-3]。特别是在一些高海拔地区，其昼夜温差较大，由此引发的温度裂缝导致结构破坏的案例屡见不鲜。针对狭长型结构的温度作用，人们往往通过设置伸缩缝的的方式降低结构的温度应力。大量的工程实例也表明在水工结构中设置温度缝是很好的举措[4-6]。在水工结构中设置温度缝，虽然可以有效地减小温度收缩产生的变形，但会降低整个结构的防水性，同时在高烈度的地震区域，温度缝的存在也会降低结构的整体性，对结构的抗震十分不利。目前对水工结构的研究主要侧重于温度或地震单独作用于结构[7-13]，对于同时考虑温度和地震作用下的结构优化研究较少，因此，如何在温度和地震作用下对水工结构进行优化设计，使结构在温度和地震作用下均具有较强的抗力，将对结构设计具有重要的参考意义。

遗传算法[14-16]是一种基于"适者生存"的高度并行、随机和自适应的优化算法,通过复制、交叉、变异将问题解编码表示的"染色体"群一代代不断进化,最终收敛到最适应的群体,从而求得问题的最优解或满意解。其优点是原理和操作简单、通用性强、不受限制条件的约束,且具有隐含并行性和全局解搜索能力,在组合优化问题中得到广泛应用。本文结合某泄槽溢洪道结构，比较了有无温度缝措施下在温度作用和地震作用下的结构应力分布特性，同时，对温度和地震共同作用下的温度缝的位置和数量进行优化设计，针对该跨沟拱形溢洪道结构的特殊性，采用遗传算法，考虑以多个位置的应力组合，通过变权重的方法进行优化。并得出最佳的优化设计方案，从而对水工结构温度缝的优化设计提供一定的参考。

1 工程背景及有限元模型

某水电站位于四川省雅砻江干流上，其洞式溢洪道进口位于左岸滑移拉裂变形体右侧，出口正对雅砻江主河道，溢洪道总长1 110 m(水平投影长度)，由进水渠段、控制闸段、无压洞段、明槽段和出口段组成。受地形地质条件制约泄槽需跨越冲沟，因此采用跨沟拱形结构作为泄槽的基础，工程处于高海拔山区，昼夜温差大。洪道泄槽段地形波状起伏、沟梁相间，地形完整性较差，地基不均匀沉降问题突出。

计算模型为跨沟拱形结构，考虑了地层岩性的影响，按照实际地形以及场地条件进行建模。跨沟结构两侧场地平台全部考虑。整个计算模型见图1。

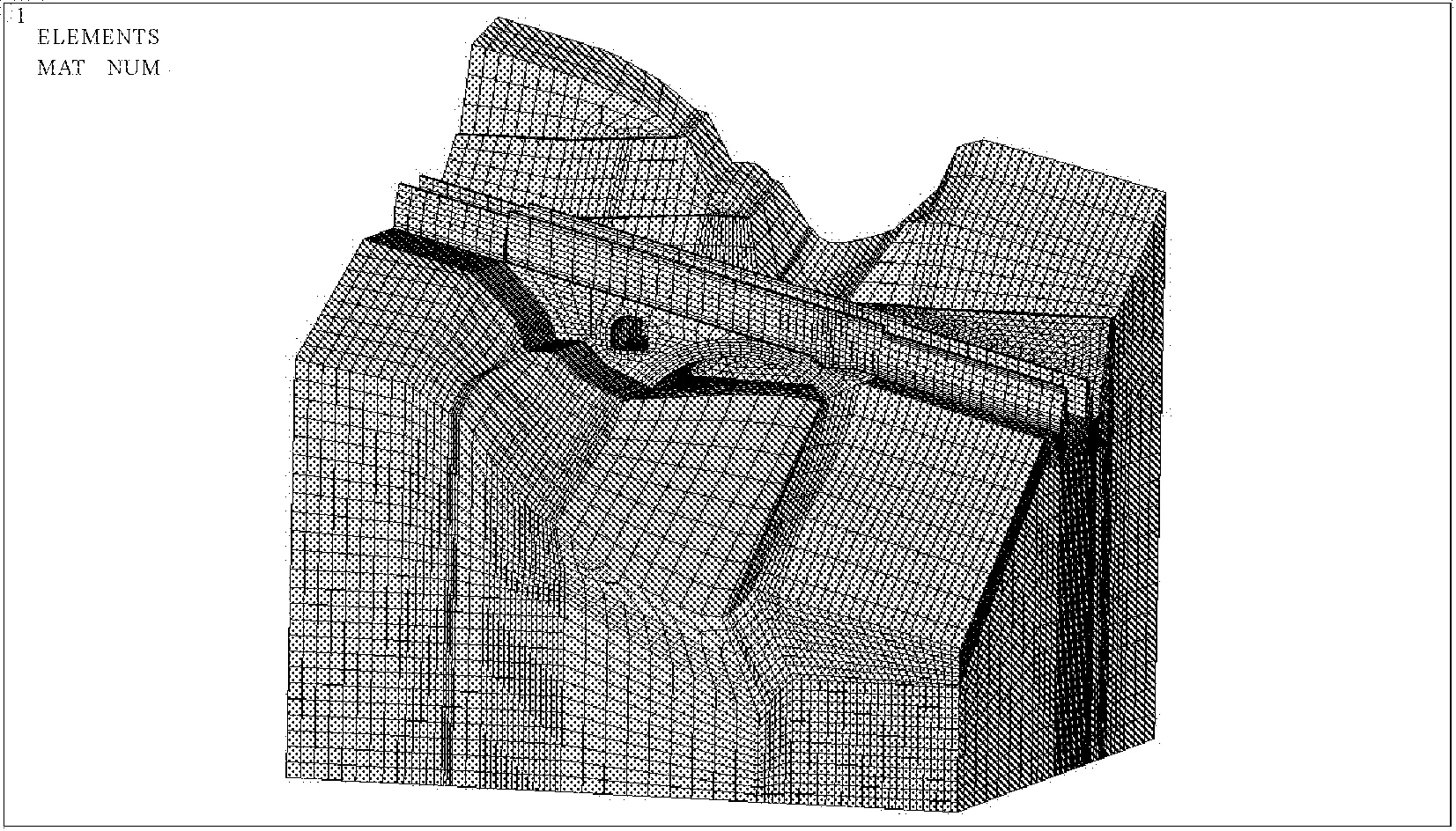
图1 溢洪道结构有限元模型

查询该地区2010年9月至2014年9月的实测温度资料，得知该工区日温差较大(日温差最大可达23℃左右)，特别是当寒流来袭时，泄槽结构表面温度骤降对结构安全十分不利，因此对运行期该水工结构进行温度作用分析是十分必要的。结构热学和力学参数如表1所示。

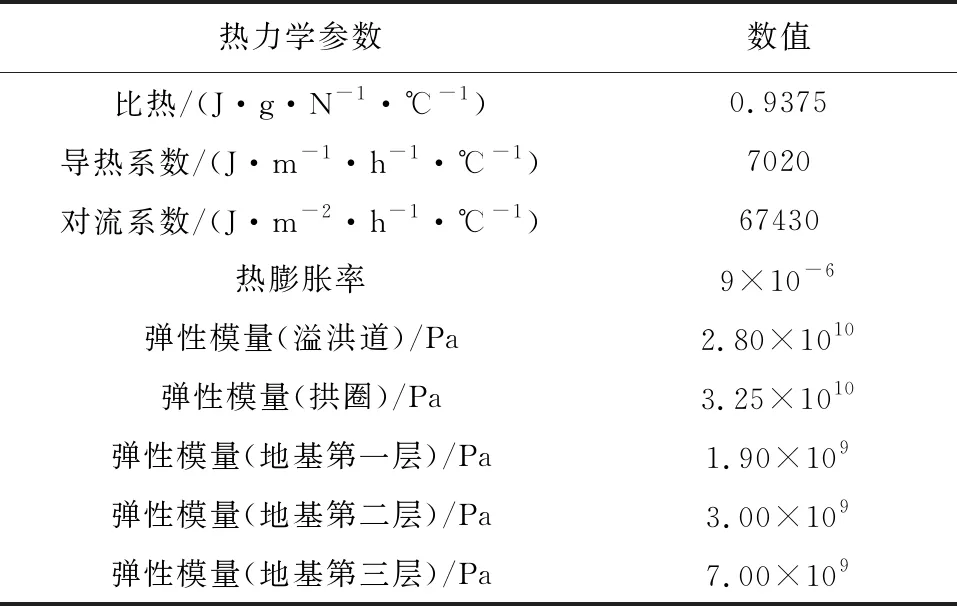
表1 溢洪道结构热力学参数

2 温度作用下结构应力分析

2.1 未设置温度缝时结构应力分析

若整个泄槽结构未设置温度缝，以某典型日极端降温工况(昼夜温差达到23℃)进行计算，有限元模型底面和四周侧面采用绝热边界，混凝土及山体与空气接触采用对流边界。考虑跨沟拱形结构的自重与极端温降工况共同作用，整个结构主拉应力如图2所示。

图2 溢洪道结构主拉应力

由图2中可以看出整个泄槽结构最大温度应力达到5.83 MPa，图中黑色区域为超出混凝土抗拉强度的区域，可以看出整个泄槽结构几乎全部处于超出抗拉强度状态。计算模型沿顺水流方向的最大应力为5.61 MPa，横水流方向最大应力为2.33 MPa，竖向最大应力为2.67 MPa。计算模型沿顺水流方向长度超过300 m，可知温度应力沿顺水流方向的累积效果十分明显。需要在顺水流方向设置温度缝降低结构的顺水流向温度应力。

2.2 设置温度缝时结构应力分析

由于未设置温度缝时，整个泄槽结构温度应力较大，因此初步考虑沿顺水流方向设置4条温度缝，依旧采用上一节介绍的温降作用工况。泄槽结构的主拉应力如图3所示。

图3 溢洪道结构主拉应力

由图3中可以看出整个泄槽结构最大温度应力达到5.61 MPa，在设置了温度缝后在温度缝设置附近应力减小效果明显，超出抗拉强度范围大幅减少。计算模型沿顺水流方向的最大应力为5.44 MPa，横水流方向最大应力为2.24 MPa，竖向最大应力为2.09 MPa。温度应力沿顺水流方向得到一定程度的释放，由此可知，考虑温度作用下温度缝的设置对整个结构的温度应力的减小是十分有必要的。

3 地震作用下结构应力分析

3.1 黏弹性边界算例验证

黏弹性边界是在边界处节点的法向和切向施加弹簧和阻尼器，来考虑无限介质的辐射阻尼和恢复性能。弹簧和阻尼器可以并连成一个元件，元件的一端与边界处的节点耦合，另一端设置为固定支座。图4为人工边界物理意义示意图。

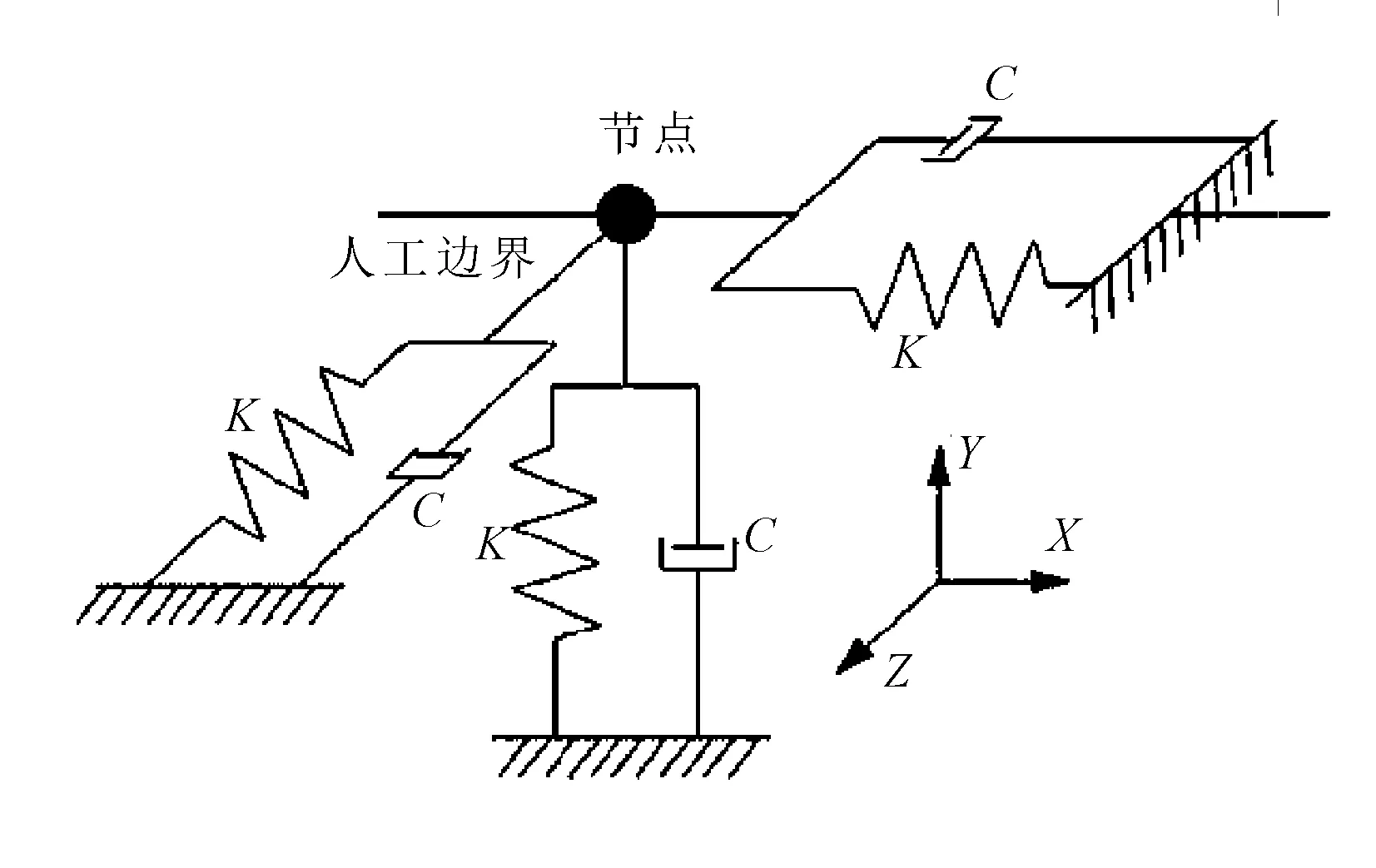
图4 黏弹性人工边界

考察三维均匀弹性半无限空间，从底部人工边界入射平面S波的动力响应。入射位移脉冲波方程为：

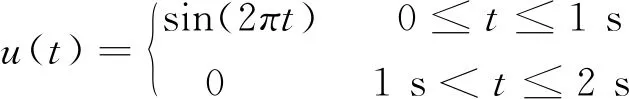
(1)

从三维弹性半无限空间选取600 m×600 m×600 m的有限区域，在外侧和底侧的节点上施加三个方向的弹簧单元，模拟黏弹性边界。选择顶面中心和底面中心两点作为控制点，如图5所示。所有地基参数如表2所示。

图5 有限元模型

物理特性数值地基密度/(kg·m-3)2000泊松比0.2弹性模量/GPa2.4压缩波波速/(m·s-1)9×10-6时长/s2时间步长/s0.01

在S波入射情况下，两个控制点的位移时程的数值解和理论解分别如图6、图7所示。

比较图6和图7可知，两个控制节点的水平位移时程数值解与理论解基本一致，顶点C2的水平位移最大值为入射S波位移最大值的两倍。

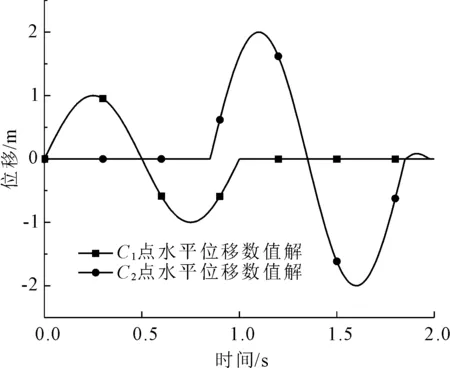
图6 水平位移时程图

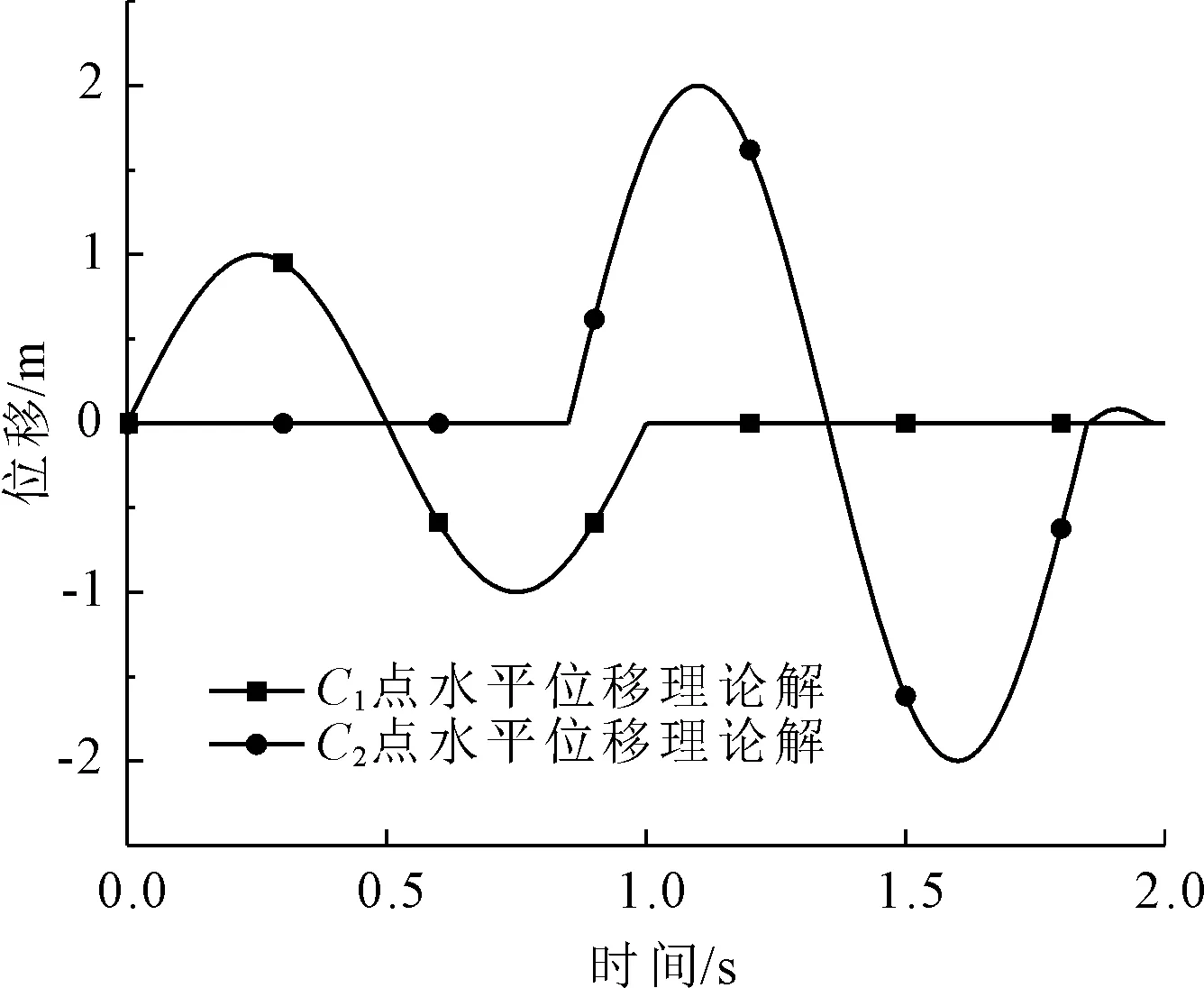
图7 水平位移时程图

在S波入射时，地基底面中心点与表面中心点的位移时程曲线与理论解接近一致，可知本文所用黏弹性边界是准确的，可以将其应用于跨沟拱形结构的地震动分析中。

3.2 未设置温度缝时结构应力分析

计算中采用场地地震波，该结构地处四川境内，水平向设计地震动为0.287g，竖向设计地震动为0.191g。图8为归一化的横水流地震加速度时程。

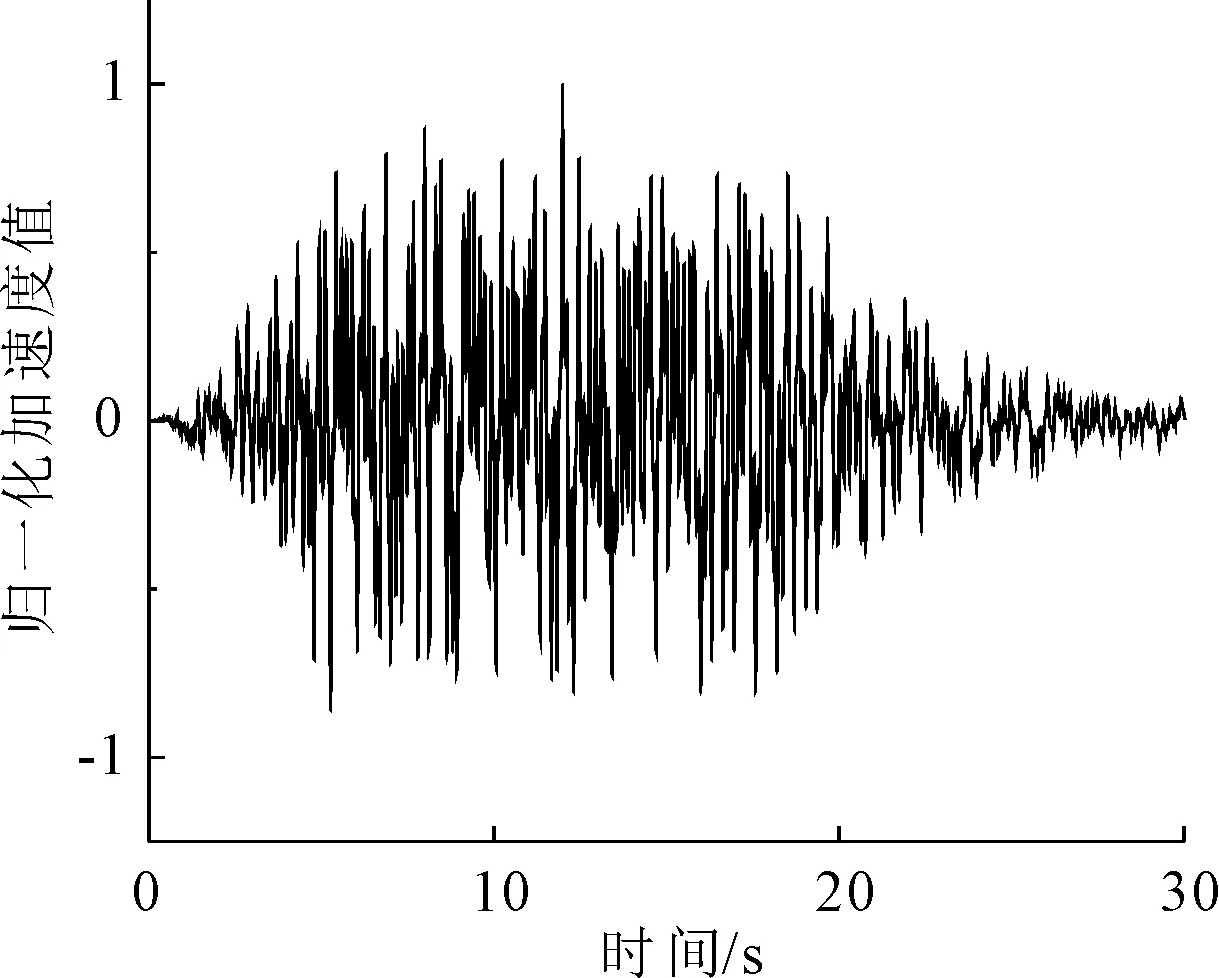
图8 水平向地震动加速度时程图

提取设计地震动下，跨沟拱形结构在设计地震动下的主拉应力最大值如图9所示。

图9 溢洪道结构主拉应力

由图9可知，在未设置温度缝时，在设计地震动作用下，泄槽结构沿顺水流方向最大拉应力达到3.50 MPa。横水流和竖向温度应力最大值分别为1.85 MPa和1.55 MPa，主拉应力的最大值为3.85 MPa，出现在拱圈圈顶附近。整个跨沟拱圈结构的整体性较好，拱圈圈顶附近结构应力较大，说明拱圈是整个跨沟拱形结构最重要的受力部位。

3.3 设置温度缝时结构应力分析

当采用上一节中同样的温度缝的位置和数量的设计工况，重新计算在设计地震动下整个跨沟拱圈结构应力，跨沟拱形结构在设计地震动下的主拉应力最大值如图10所示。

图10 溢洪道结构主拉应力

由图10可知，设置了温度缝后，在设计地震动作用下，泄槽结构沿顺水流方向最大拉应力达到2.58 MPa。横水流和竖向温度应力最大值分别为2.89 MPa和2.55 MPa，主拉应力的最大值为7.72 MPa。泄槽结构顺水流方向的应力相比于没有温度缝时有一定程度减小，但是横水流方向的应力和竖向应力却存在显著增加，由此可知，温度缝的位置不同会引起整个跨沟拱形结构抗震性能的改变，因此需要对温度缝的位置进行优化设计，以便跨沟拱形结构具有较好的抗震能力。

4 温度地震共同作用下结构优化设计

4.1 设计变量

整个跨沟拱形结构的设计变量包括温度缝的位置和数量，将跨沟拱圈结构上部划分为5个区域，假设在5个区域内均可考虑设置一条温度缝或者不设置温度缝，其代表为5个影响因素。将每个区域均匀划分为4段，如图11所示。如果分别出现在1、2、3和4这四个位置，则对应的因素水平的变量值也分别为1、2、3和4；每一段如果不设置温度缝，则该因素水平的变量值为0。

4.2 目标函数

常规温降和地震共同作用与跨沟拱形结构，其应力最大值的出现位置主要集中在拱圈圈顶，左侧拱脚处和回填区与拱圈基础平台段连接的变截面处，如图12所示。如果采用单一的三个控制位置选择其中最大的应力值作为评判依据，往往不能更好地显示出结构整体的受力特性。相反，如果采用多个控制位置的应力的有效组合，则可充分达到提高整个跨沟拱形结构的受力评价效果。此时三个区域的权重占比也是需要考虑的问题。考虑计算校核地震动和温度变化工况下的组合工况，基于两种工况下的三个位置主拉应力变化率作为权重的判断指标，建立目标函数如下:

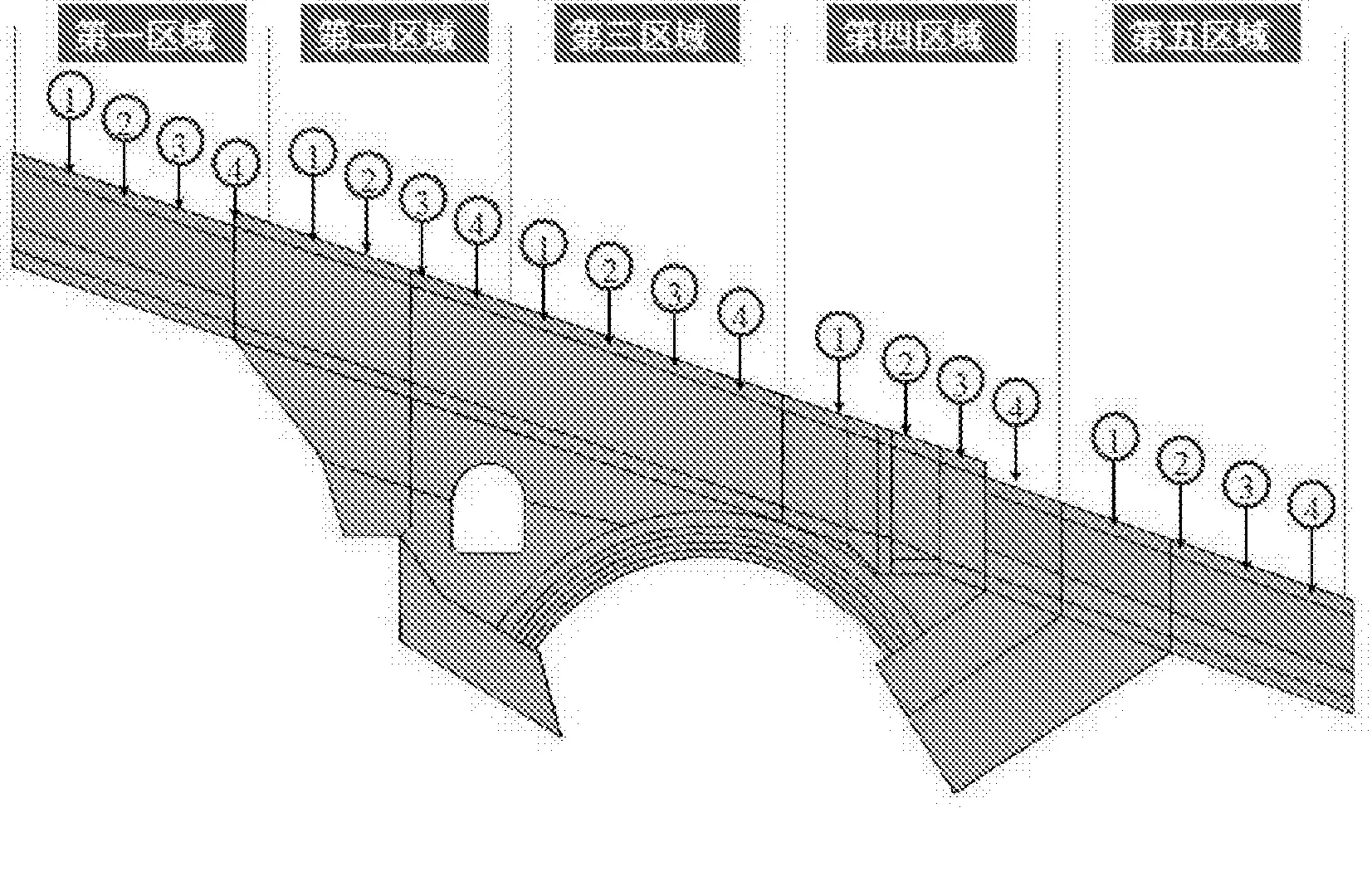
图11 溢洪道结构优化区域图

minF

(2)

式中：γi为i位置处的应力权重；Fi为i位置处的主拉应力值。

4.3 遗传算法优化

按照上图所示的遗传算法的优化步骤对目标函数进行优化设计，种群规模设置为10，根据预定的目标函数对每个个体进行适应度值的评价，采用随机联赛选择方法，并保留最佳个体的策略，交叉概率为1，变异概率为0.05，遗传算法设置最大遗传次数为100，在迭代到80次时目标函数(见图13)趋于稳定值3.801 MPa。

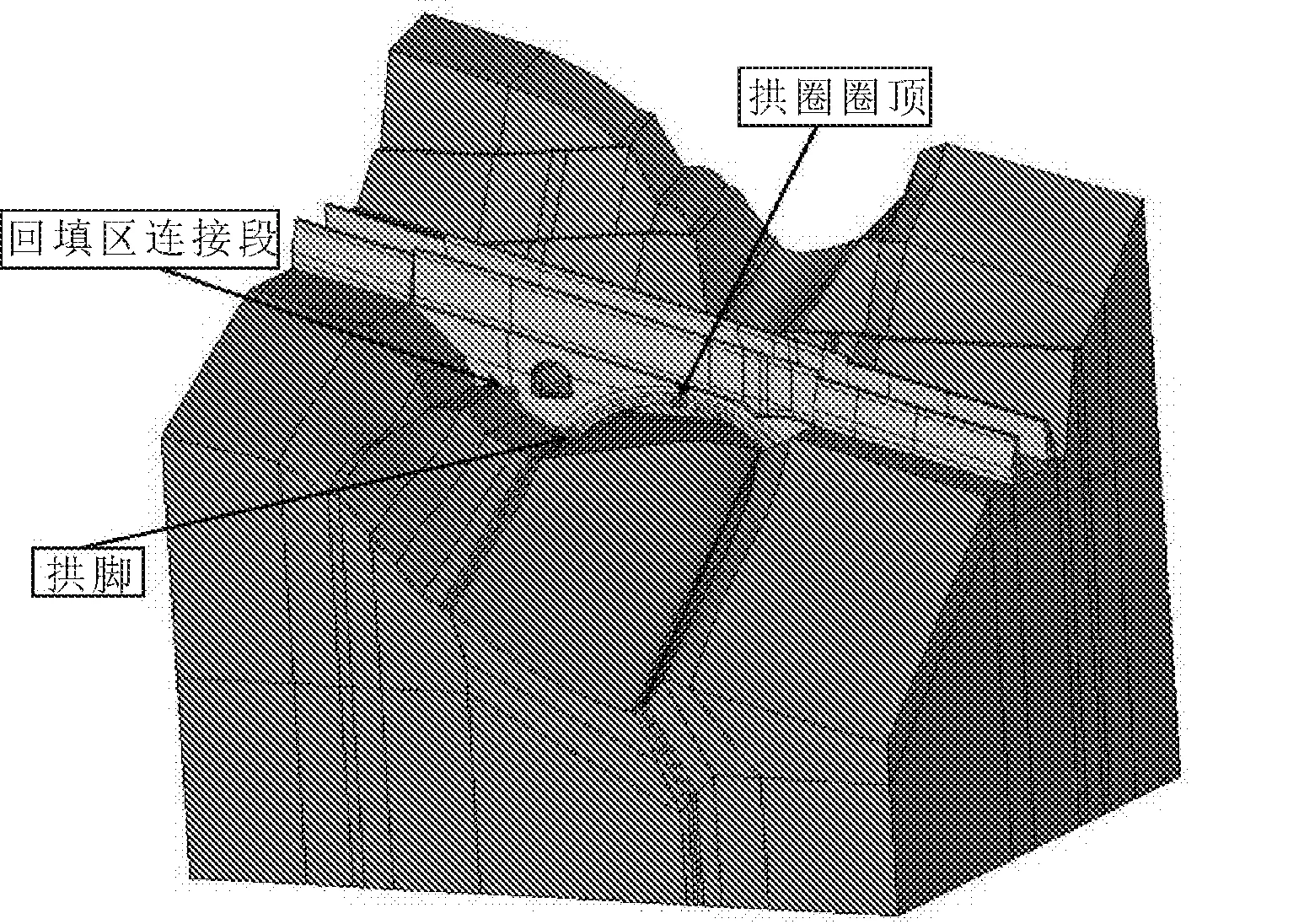
图12 溢洪道结构图

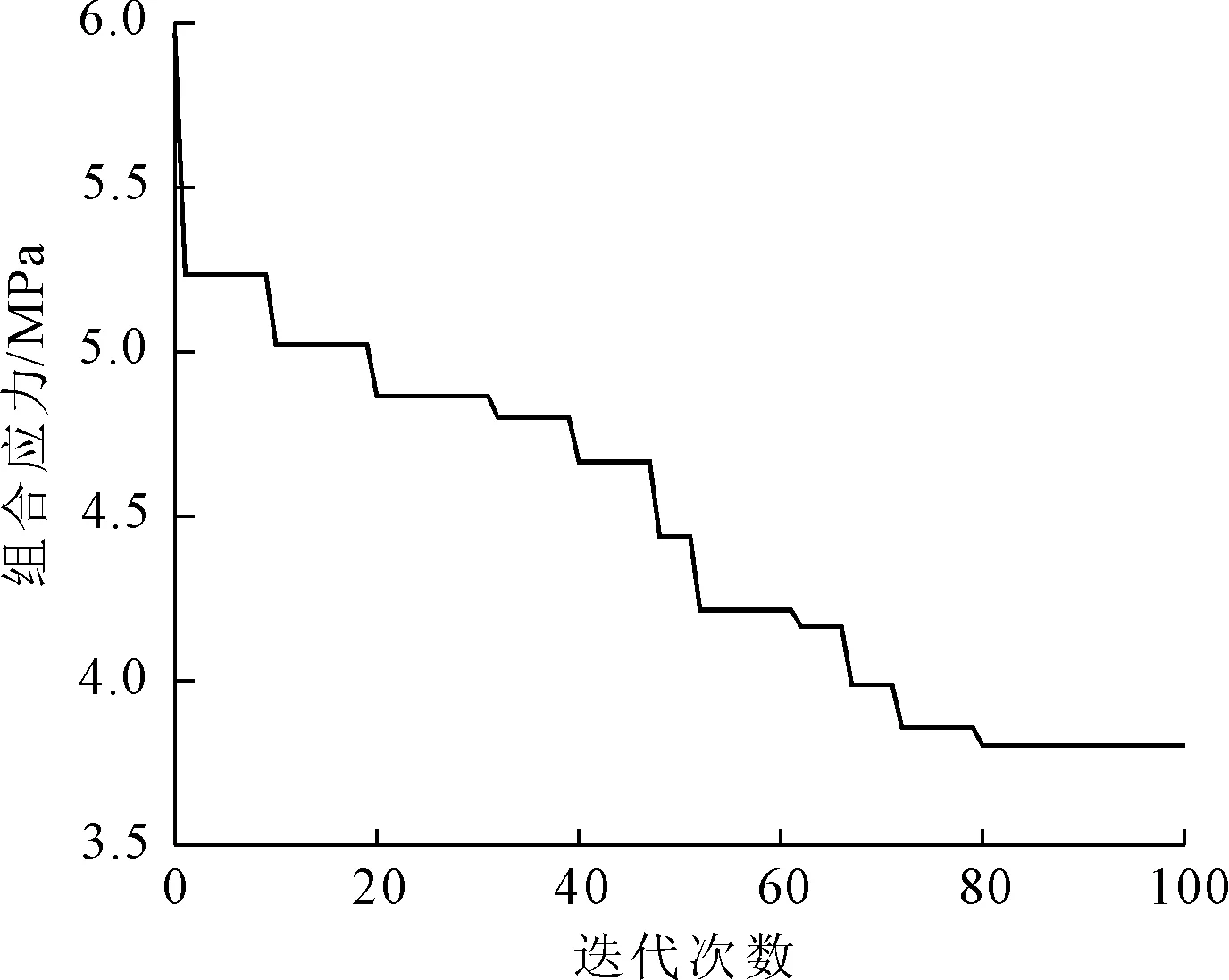
图13 组合应力随迭代次数变化关系

遗传算法对整个跨沟拱形结构温度缝位置的优化结果如表3所示。

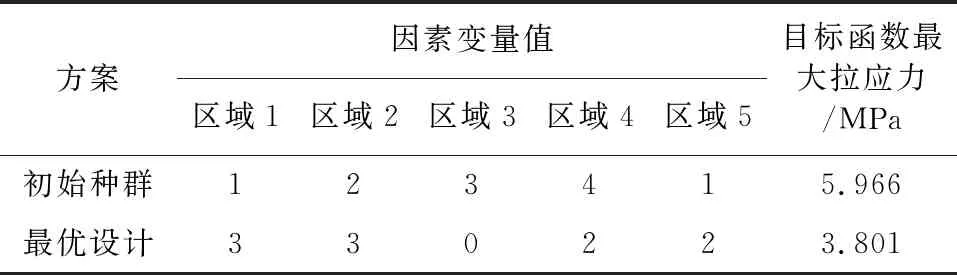
表3 遗传算法优化前后对比

从表3中可以看出，采用遗传算法优化后，目标函数的最大拉应力从5.966 MPa减小到3.801 MPa，优化率达到36.3%。因此在拱圈结构优化设计时，选择合适的分缝位置和分缝数量对于整个跨沟拱形结构的综合抗力具有十分重要的意义。

5 结 论

本文以某实际泄槽溢洪道结构为工程背景，研究了温度缝对结构抗震能力的影响。结果表明，温度缝的存在对降低溢洪道结构的温度应力效果明显，但是会加大溢洪道结构在地震作用下的应力。针对这一问题，本文以温度缝位置和数量作为设计变量，并将不同工况下结构多个位置的应力进行变权重组合作为目标函数，通过遗传算法对结构的温度缝位置和数量进行了优化。本文的研究可为同类型工程设计提供参考。