蚊香盘式液流通道磁流变阀压降及响应性能研究

胡国良 郑凯阳

(华东交通大学载运工具与装备教育部重点实验室， 南昌 330013)

0 引言

传统液压控制阀中含有活动的机械构件，从而使其结构较为复杂、体积大、加工要求高，同时存在控制难、噪声大等问题[1-2]。智能材料磁流变液能够根据外加磁场强度变化而发生瞬间变化，以磁流变液为工作介质的磁流变阀能较好地解决这些问题。磁流变阀无相对移动部件，可直接通过电信号控制，因而结构简单、工作可靠，且响应迅速、易于控制，能够满足液压元件和系统要求的高效率、环保以及低能耗[3-6]。

国内外针对提高磁流变阀压降范围进行了许多研究。根据液体流道设计样式不同，可分成轴向流动式、径向流动式以及轴向-径向复合型流动式磁流变阀[7-20]。轴向流动式磁流变阀依靠增加轴向阻尼间隙长度使压降升高，但易造成阀体积过大。GRUNWALD等[7]完成了轴向流动式阀体的结构设计和仿真分析，输入电流4.5 A时，压降为1.5 MPa。径向流动式磁流变阀流道与阀体进出口垂直，相比于轴向式磁流变阀可产生更大的压降。胡国良等[8-10]通过仿真和实验测试对比分析了径向流和圆环流磁流变阀压降性能，验证了径向流有更大的压降可调范围；同时提出一种两级蜿蜒式径向流磁流变阀，依靠多个阀芯以扩大生成磁流变效应范围，压降在加载电流0.8 A时可达5.81 MPa，但阀体外形尺寸较大[11]。轴向-径向复合型流动式磁流变阀充分利用了磁力线走向，其压降能力得到进一步优化。文献[12-14]设计了一种把两个以上完全一样的磁流变阀单元组合串联在一起的模块式磁流变阀，能产生较大压降。NGUYEN等[15-16]利用黄金分割算法与局部二次拟合方法，通过有限元参数化设计语言构建优化程序对磁流变阀进行优化，仿真结果表明，轴向-径向复合流道的磁流变阀具有较高的压降。胡国良等[17-19]提出了一种混合流动式磁流变阀，实验结果表明，该阀能产生2.5 MPa的压降；同时依靠改变部分零件导磁属性，提出一种改进型径向流动式磁流变阀，最大压降可达4.2 MPa[20]。

通过增加线圈匝数使单线圈变成双线圈结构，改变液体流道结构，由圆环轴向流变为圆盘径向流均可以增大压降可调范围。这些改进结构的阀的压降调节范围和响应特性大多未能取得较好的成效，只能在低压小流量液压系统中工作，因而限制了应用范围。本文设计一种蚊香盘式液流通道磁流变阀，在不改变常规径向流磁流变阀外形尺寸前提下，通过添加具有蚊香盘式弧形隔磁挡板，增加有效阻尼间隙长度，以期增大压降可调范围，有效改善其压降响应。

1 结构与工作原理

磁流变阀结构设计时，首先要保证外加磁场的磁力线走向垂直于磁流变液流经的液流流道，使其剪切应力达到最大，增大磁流变效应；其次是增大有效阻尼间隙长度，使压降调节范围更广；最后根据实际情况选择合理的阻尼间隙，避免工作时堵塞。综合以上因素，在常规径向流磁流变阀基础上设置弧形隔磁挡板，形成图1所示蚊香盘式液流通道磁流变阀，使得磁流变阀内磁流变液沿液流通道曲线流动，增大了有效阻尼间隙长度，同时也保证了磁流变液在每一段阻尼间隙内的流动方向都与磁力线方向垂直，充分利用了磁力走向，提高了磁场利用率。

图1 蚊香盘式液流通道磁流变阀结构图Fig.1 Schematics of MR valve with mosquito-plate fluid flow channels1.螺钉 2.端盖 3.密封圈 4.阀套 5.阻尼圆盘 6.蚊香盘式弧形挡板 7.绕线架 8.定位盘

所设计的磁流变阀径向阻尼间隙为2 mm，圆环轴向阻尼间隙为5 mm，中心孔半径为5 mm。如图1所示，阀芯外缘设计有4个小支脚，与绕线架内壁过渡配合；阻尼圆盘左右两端加工有和蚊香盘式弧形隔磁挡板相匹配的槽，并通过插入蚊香盘式挡板，两个定位盘与其紧贴，达到固定阻尼圆盘的作用；定位盘与阻尼圆盘之间被蚊香盘式挡板分隔出的液流通道即为有效阻尼间隙，阻尼间隙内的液体流动分为圆管形、螺旋形和圆环形3种形式。磁流变阀的左右两个端盖以及左右两个定位盘间的液体流道即为圆管阻尼间隙；由左右两个定位盘和中间阻尼圆盘之间的部分，被两个蚊香盘式弧形隔磁挡板分隔出的通道即为螺旋型阻尼间隙，其中定位盘孔径附近一部分为圆盘形阻尼间隙；阻尼圆盘与绕线架之间即为圆环形阻尼间隙。这些阻尼间隙内产生的压降共同构成了该阀体的总压降，有效地增大了阻尼间隙长度，与此同时，蚊香盘式液流通道与外部磁场垂直，磁感线利用更加充分。依靠输入电流变化实时控制磁感应强度，进而改变剪切屈服应力，可连续调节磁流变阀压降，起到压力控制阀的作用。

2 压降数学模型

由图1a可知，蚊香盘式液流通道的磁流变阀中，牛顿流体有2个圆管型、1个圆环型工作流道；非牛顿流体有2个圆盘型和2个螺旋型工作流道。根据阀内部流体流动形式，将其分成7个区域。图2所示为每个部分的划分与压降分布情况。

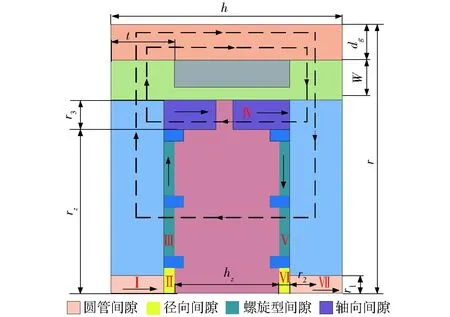
图2 区域划分和压降分布情况Fig.2 Regional division and pressure drop distribution

根据磁流变液与磁力线是否相互垂直，牛顿流体中，圆管流为区域Ⅰ和Ⅶ；圆环流为区域Ⅳ；非牛顿流体中，圆盘流为区域Ⅱ和Ⅵ；螺旋流为区域Ⅲ和Ⅴ；区域Ⅱ和区域Ⅵ的压降Δp2和Δp6以及区域Ⅲ和区域Ⅴ中的压降Δp3和Δp5皆包括粘滞压降和磁滞压降两部分。因此总压降Δp可表示为

Δp=Δp1+Δp2+Δp3+Δp4+Δp5+Δp6+Δp7=
Δp1η+Δp2η+Δp2τ+Δp3η+Δp3τ+Δp4η+
Δp5η+Δp5τ+Δp6η+Δp6τ+Δp7η

(1)

式中 Δp——具有蚊香盘式液流通道结构的磁流变阀总压降

Δp1η、Δp2η、Δp3η、Δp4η、Δp5η、Δp6η、Δp7η——区域Ⅰ～Ⅶ中的粘滞压降

Δp2τ、Δp3τ、Δp5τ、Δp6τ——区域Ⅱ、Ⅲ、Ⅴ和Ⅵ中的磁滞压降

区域Ⅰ和区域Ⅶ为牛顿流体圆管流，其粘滞压降为

(2)

式中η——零场粘度

q——体积流量

r1——圆管阻尼间隙

h——绕线架长

hz——阻尼圆盘厚度

区域Ⅳ内为牛顿流体圆环型间隙流动，因为磁感线和液流方向相同，其粘滞压降为

(3)

式中rz——阀芯半径

r3——区域Ⅳ处圆环工作间隙

r2——圆盘工作间隙

为求出蚊香盘式液流通道内的压降变化，须求出螺旋通道长度和类扇形区域面积，首先对该螺旋线进行分析计算，如图3所示，内螺旋通道L1中点曲线方程可表示为

(4)

式中δ——蚊香盘式弧形隔磁挡板厚度

C——节距，即同一蚊香盘式弧形隔磁挡板相邻两圈距离

ρ1——向径，即阀芯中心为极点，挡板曲线一点与中心点连线长度

r——蚊香盘式液流通道起点底圆半径

θ1——螺旋角，即向径与水平线夹角

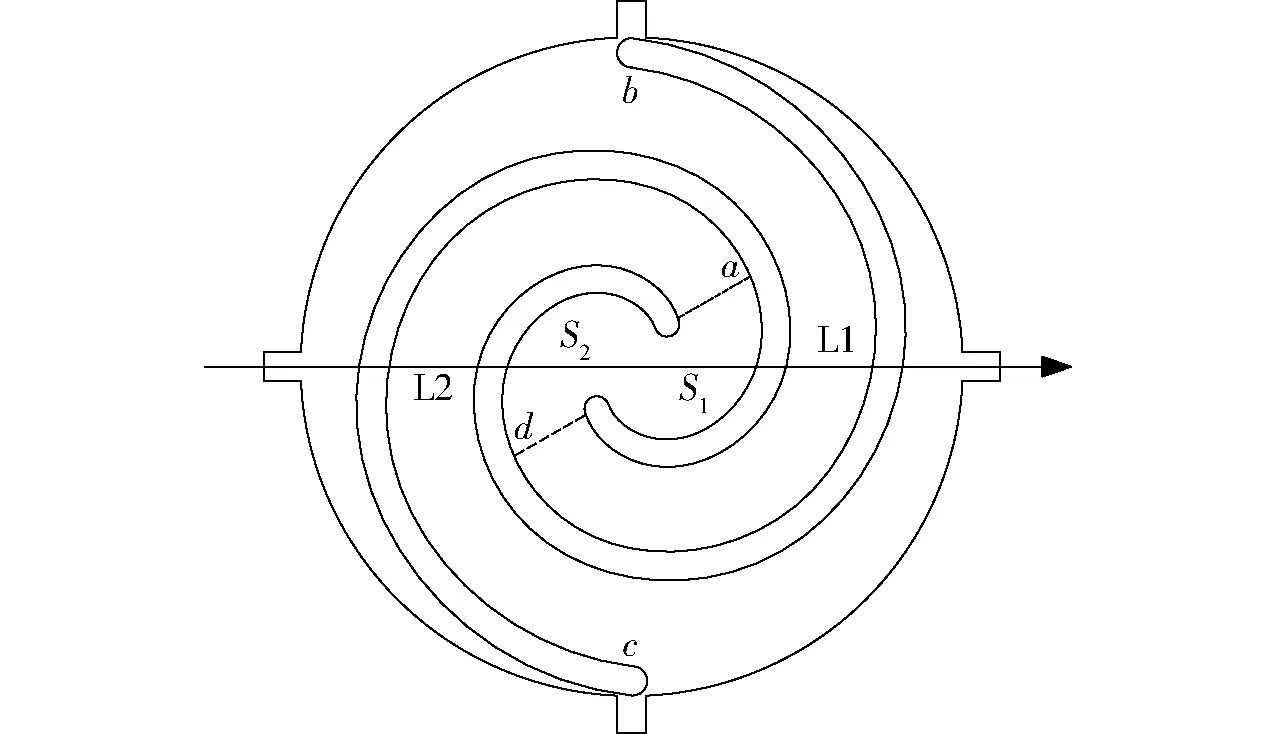
图3 蚊香盘式弧形隔磁挡板结构简图Fig.3 Schematic of mosquito-plate structure

外螺旋通道L2中点曲线方程可表示为

(5)

内螺旋通道L1长度为

(6)

式中ρ′1——内螺旋通道终点处极径

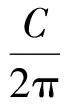
外螺旋通道L2长度为

(7)

式中ρ′2——外螺旋通道终点处极径

内侧蚊香盘式挡板bd段曲线方程为

(8)

式中D——蚊香盘式液流通道宽度

θ′1——内侧蚊香盘弧形隔磁挡板起始螺旋角

θ′2——外侧蚊香盘弧形隔磁挡板起始螺旋角

外侧蚊香盘式挡板ac段曲线方程为

(9)

中心扇形区域面积计算公式可表示为

(10)

为方便计算，将基准坐标轴顺时针旋转45°，则两个扇形区域面积分别为

(11)

(12)

取一个等效圆，其半径为

(13)

扇形区域内压降公式为

(14)

(15)

式中c——修正系数，取2～3

τy——剪切屈服应力B——磁感应强度

蚊香盘式液流通道内粘滞压降为

(16)

蚊香盘式液流通道内屈服压降为

(17)

综上，可得到蚊香盘式液流通道磁流变阀的总压降Δp为

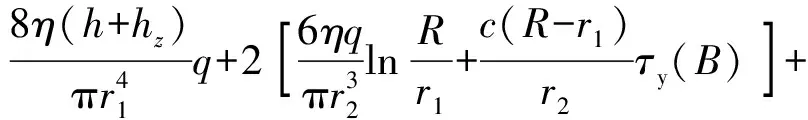
(18)

3 电磁场仿真

3.1 磁流变液特性

工作介质磁流变液选择重庆材料研究所生产的MRF-J01T型MRF[6]。磁流变效应发生时，磁感应强度B随磁场强度H增大；剪切应力在达到饱和之前，磁流变液相对磁导率大于2.5；当磁感应强度B从0 T增至0.5 T时，剪切屈服应力τy从0 kPa增至约65 kPa。

选择最小二乘法对τy-B曲线完成三次多项式拟合，获得τy与磁感应强度B间的关系式

τy=a3B3+a2B2+a1B+a0

(19)

式中，a0=0.018 2 kPa，a1=-48.464 4 kPa/T，a2=865.390 1 kPa/T2，a3=-984.274 2 kPa/T3。

3.2 压降性能电磁场仿真

采用有限元法对磁流变阀中的磁力线分布和阻尼间隙内的磁感应强度进行电磁场建模分析。图4为磁流变阀简化后的各部分区域实体模型等效平面图，将蚊香盘式弧形隔磁挡板部分忽略可得到对称结构。该模型由阻尼间隙、阀套、线圈、绕线架、阻尼圆盘及定位盘6个区域组成。

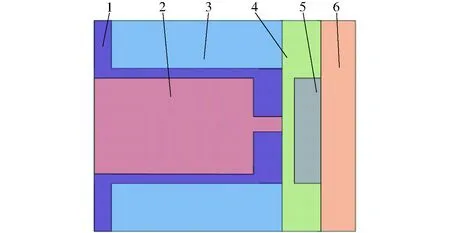
图4 蚊香盘式液流通道磁流变阀实体模型Fig.4 Entity model of proposed MR valve1.阻尼间隙 2.阻尼圆盘 3.定位盘 4.绕线架 5.励磁线圈 6.阀套

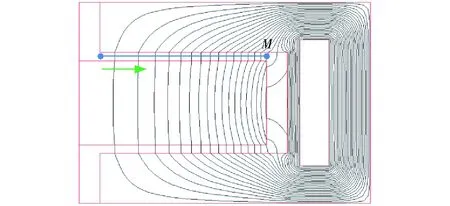
图5 磁力线分布及路径定义Fig.5 Distribution of magnetic flux lines and defined path

图6为定义的路径M处各个点的磁感应强度，径向间隙中部接近励磁线圈部分的磁感应强度缓慢增长，此间隙两侧的磁感应强度接近于0。由磁流变阀磁感应强度变化趋势可知，在径向流道M中0～40 mm路径上，磁感应强度显著上升，由0.43 T增至0.47 T，这是由于阻尼间隙距离励磁线圈越近，磁感应强度就越大。在流动通道的中间部位，磁感应强度大致处于平稳的趋势，在0.46～0.47 T之间缓慢上升，上升趋势较为平缓，在39～40 mm之间减小约0.4 T。在接近轴向流动通道时，因为这个位置磁力线与流体流向平行或者几乎没有磁力线经过，所以此区域磁感应强度迅速降为0。

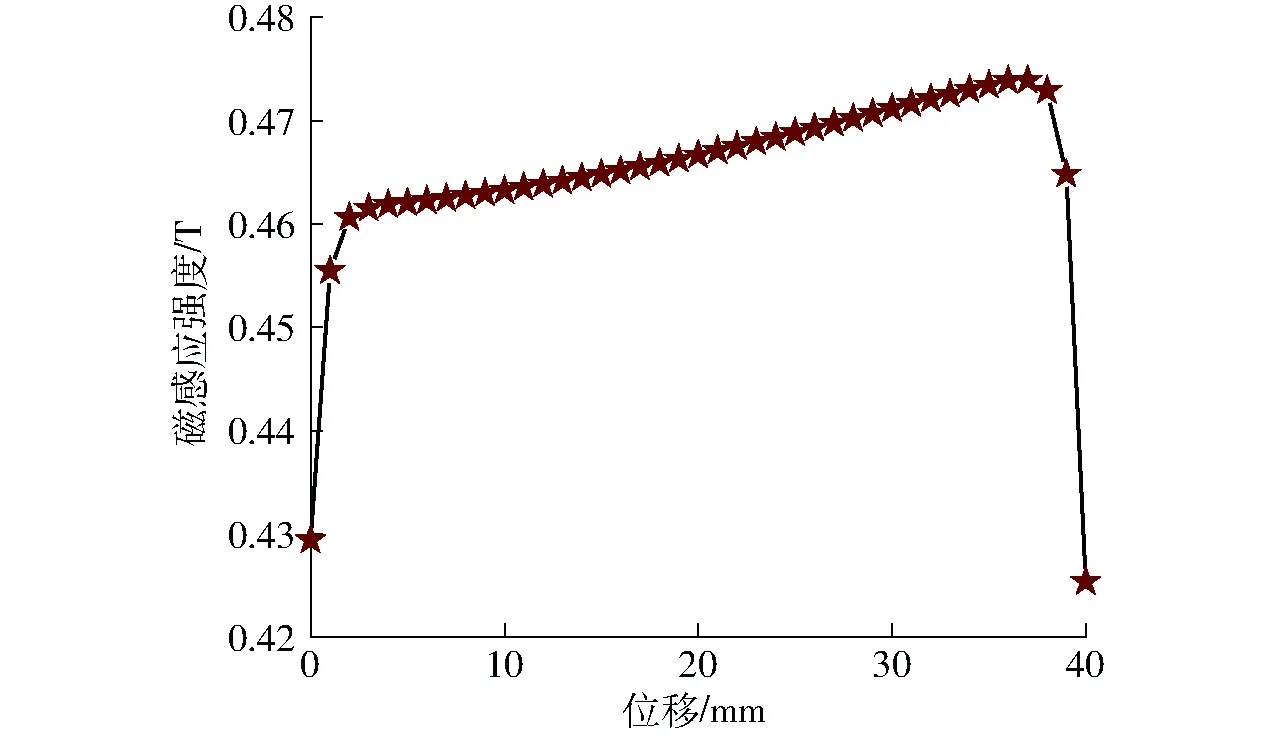
图6 路径M上磁感应强度Fig.6 Magnetic flux density along defined path

图7为平均磁感应强度及剪切应力与电流关系曲线。电流为0.2 A时，平均磁感应强度仅为0.11 T；随电流增大，平均磁感应强度迅速增加，在电流达到1.2 A之后，平均磁感应强度增速有所放缓，在2.0 A时，平均磁感应强度达到0.576 T。剪切应力随输入电流的增大而增大，当增大到一定值时基本恒定，剪切屈服应力饱和值约为71.4 kPa，约2.0 A时达到饱和。

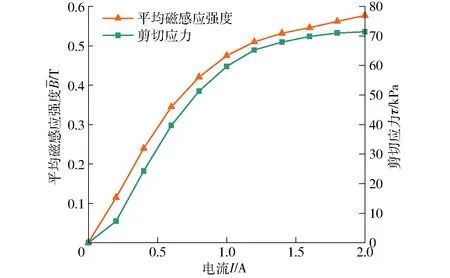
图7 平均磁感应强度及剪切应力变化曲线Fig.7 Average magnetic flux density and shear stress under applied current

图8为不同输入电流下磁流变阀压降变化曲线。磁流变阀的总压降主要来自径向流动通道与螺旋流动通道，轴向流动通道和圆管型流道所贡献的压降非常小，电流增加后可忽略不计。由图可知，随着电流的增加，压降随之增大，在1.2 A之前，压降增长很快，从0.04 MPa迅速增大到4.71 MPa，在1.2 A之后，由于平均磁感应强度增速放缓，导致压降增速变慢，到2.0 A时，压降达到5.58 MPa。

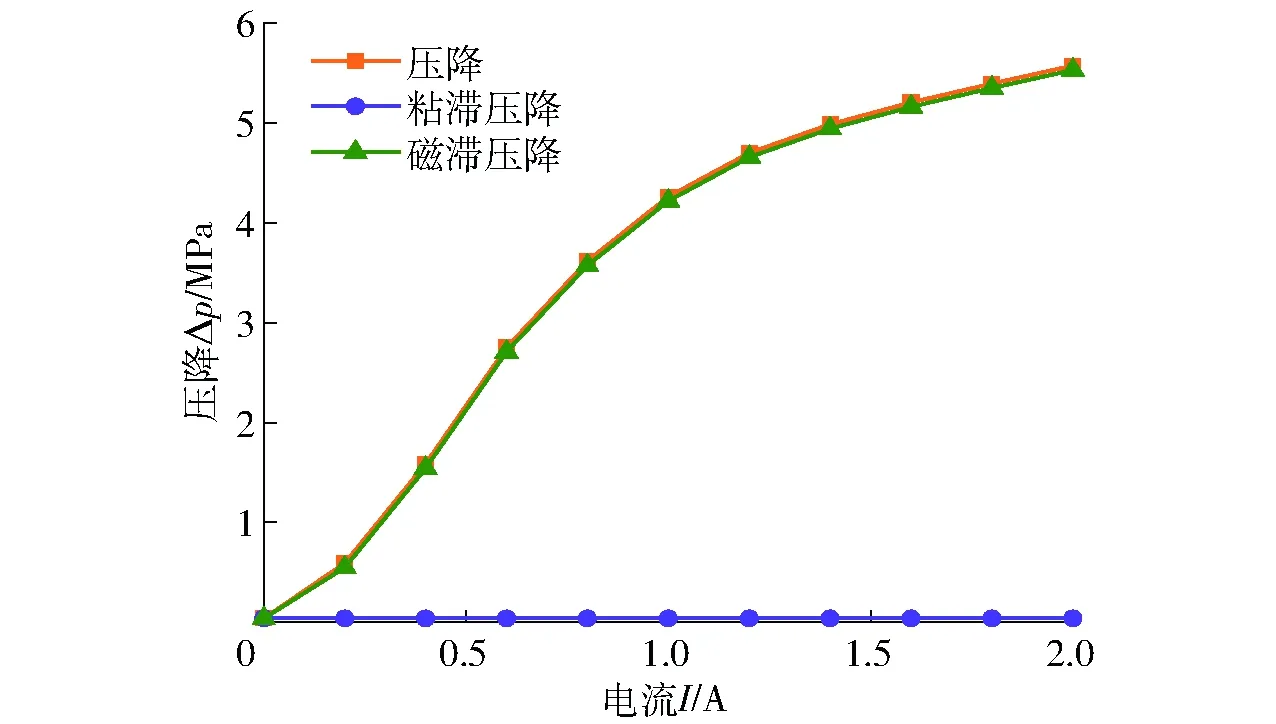
图8 压降随电流的变化曲线Fig.8 Pressure drop under applied current

4 动态性能测试

4.1 磁流变阀样机与性能测试系统

结合理论计算和仿真建模加工了图9所示蚊香盘式液流通道磁流变阀。

图9 蚊香盘式液流通道磁流变阀实物图Fig.9 Prototyping of MR valve with mosquito-plate fluid flow channels

图10为蚊香盘式液流通道磁流变阀性能测试系统。系统中动力单元由电机驱动的齿轮式定量泵组成。溢流阀Ⅰ作为安全阀连接在齿轮泵出口与阀的进口之间；溢流阀Ⅱ安装在阀出口和油箱回油口之间，实现模拟负载的设置。阀内线圈加载电流由电源Ⅰ提供，压力传感器Ⅰ和Ⅱ供电电流由电源Ⅱ提供；磁流变阀入口处压力由压力传感器Ⅰ测量，磁流变阀出口处压力由压力传感器Ⅱ测量；压力传感器Ⅰ与Ⅱ的实测压力数据实时传输到采集卡中，并传输到计算机控制界面[11]。

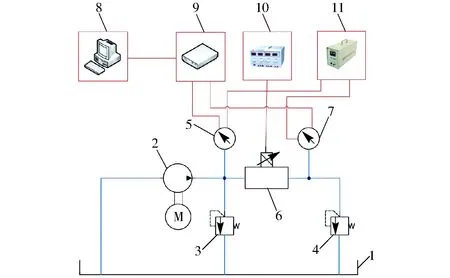
图10 磁流变阀性能测试系统原理图Fig.10 Test rig of proposed MR valve1.油箱 2.定量泵 3.溢流阀Ⅰ 4.溢流阀Ⅱ 5.压力传感器Ⅰ6.磁流变阀 7.压力传感器Ⅱ 8.主机 9.采集卡 10.电源Ⅰ11.电源Ⅱ

4.2 压降特性实验

测试过程中，手动旋动电源Ⅰ和溢流阀Ⅱ的旋钮，得到不同电流与载荷条件下磁流变阀的进出口压力，最终测得压降。实验中规定溢流阀Ⅱ旋钮角最小时为负载工况0；旋钮角变化时，溢流阀Ⅱ的开口度逐渐变小，所受载荷将增大。实验时，将旋转720°视为负载工况1；转动1 440°视为负载工况2。另外，选用流量为4、10 L/min的定量齿轮泵，以观测不同流量情况下压降变化。

图11是在负载条件1下，流量为4 L/min时磁流变阀的压力变化曲线。电流缓慢增加时，磁流变阀的进口压力呈稳步上升趋势，且渐趋饱和。因为测试系统将溢流阀Ⅰ并联在回油路中发挥稳压作用，出口压力一直保持相对稳定。进出口压力差即压降是根据进口压力和出口压力的差值获取的，所以压降也会保持一定的增量较为均匀地增大，且渐趋饱和。由于实际所绕线圈匝数略少于理论设计要求匝数，在2.0 A电流内磁流变阀的压降并未完全饱和，但是压降可调节范围较之以往磁流变阀仍提升明显。磁流变阀在电流加载到2.0 A后趋近饱和状态，最大压降可达5.1 MPa。

图12为磁流变阀在3种负载情况下的压降随电流的变化曲线。压降随电流的增加而增大，泵出口压力不稳造成压降存在一定程度的波动，但其增长势态并未改变。另外，磁流变阀在3种负载变化下的压降曲线基本相互重合，说明所设计的磁流变阀压降不受负载变化的影响。这种压降不随负载变化的特性可使磁流变阀用于控制执行机构在高频响范围内作相应运动，也可作为旁通阀控制阻尼器工作在各种减振抗震应用场合。比如可控制阻尼器直接安装在车辆座椅悬架系统上，从而提高驾乘人员的乘坐舒适性，达到满足高速和低速等不同路面工况驾驶要求的目的[11]。

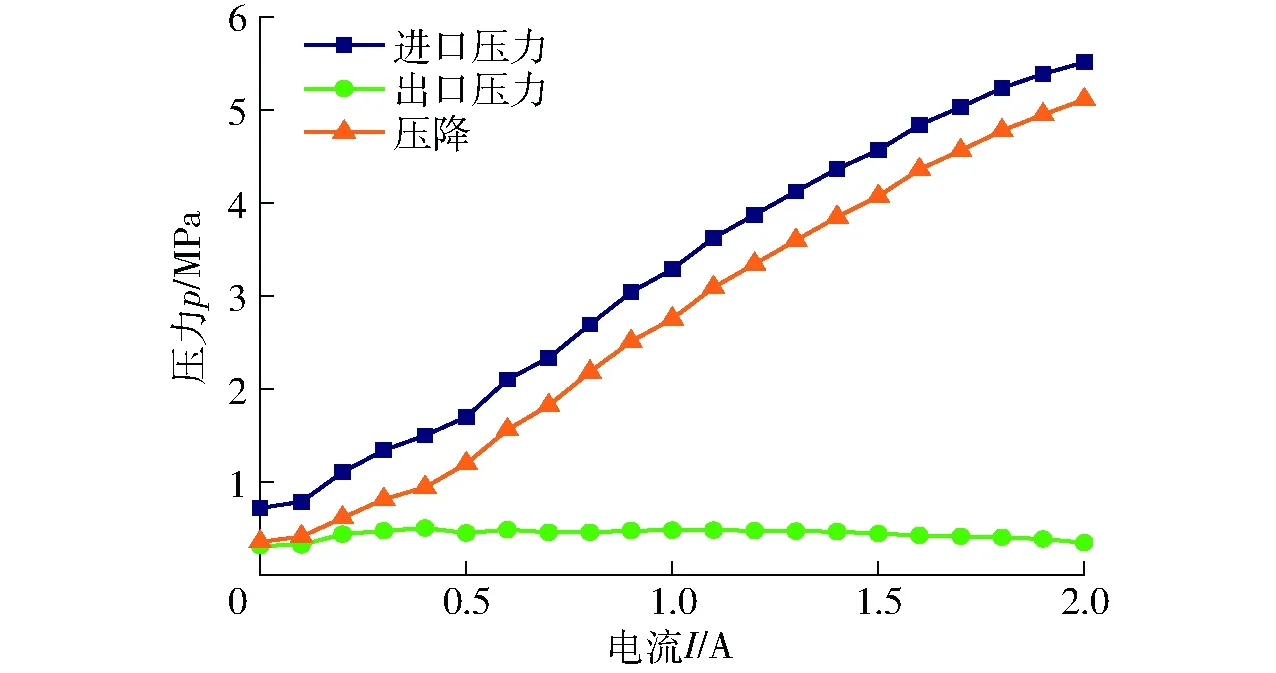
图11 负载1条件下磁流变阀的压力变化曲线Fig.11 Change of pressure with respect to current at load case 1

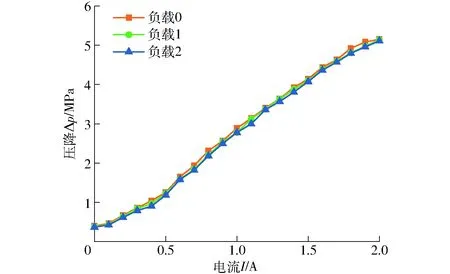
图12 不同负载工况时磁流变阀压降性能Fig.12 Pressure drop of MR valve under different load cases

图13为4 L/min流量下磁流变阀仿真压降和实验压降对比曲线。电流较小时，实验压降高于仿真压降，这是由于粘滞压降占总压降的比重较大，但是仿真数据是以Bingham模型为理论得到的，没有考虑液体的增稠效应。随着输入电流的增加，实验压降小于仿真压降，这是由于磁场介入导致的磁滞压降开始成为总压降的主导部分。另外，仿真是在磁流变液中的磁性粒子形成单链结构的前提下，得到剪切应力与磁感应强度输入之间的关系曲线，但实际上在磁场作用下形成的结构不是单链结构，因此实验中获得的饱和剪切屈服应力会更小。与此同时，组装磁流变阀组件中留有一定间隙，所以实验过程中不可避免地造成磁通量损失，这也会影响有效区域的磁感应强度，使得实验压降小于仿真压降。

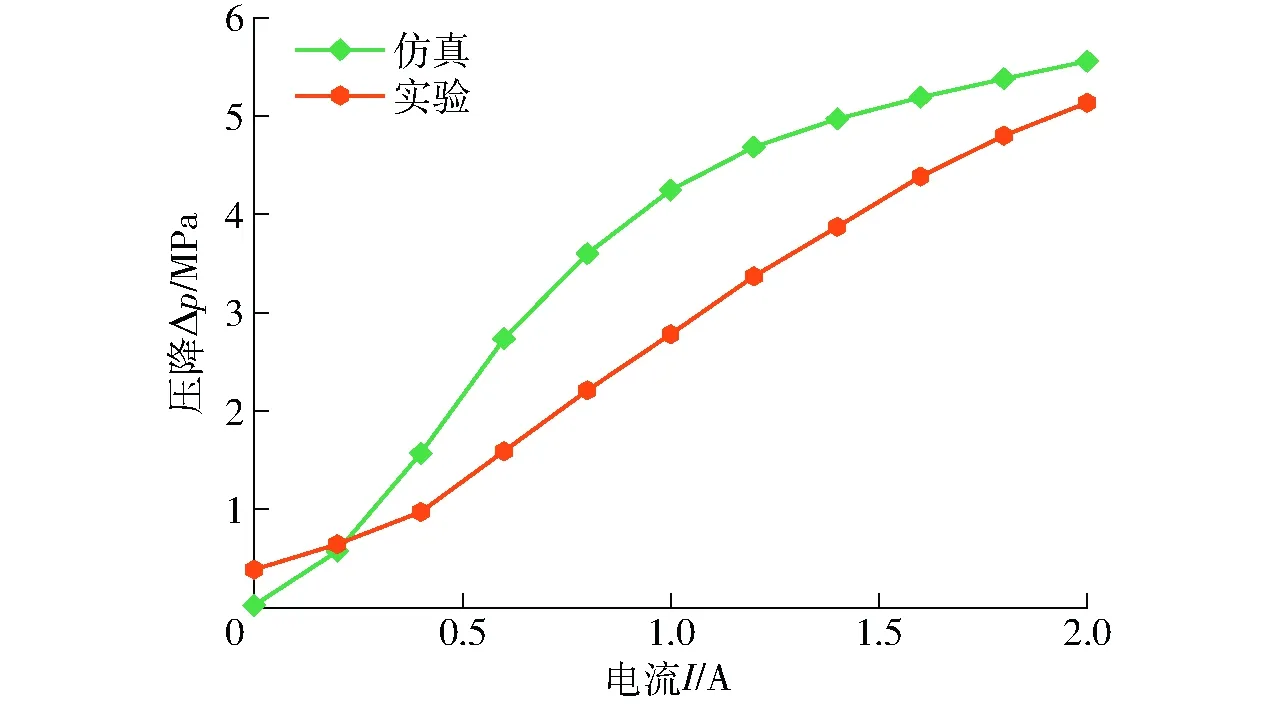
图13 仿真和实验压降对比曲线Fig.13 Comparison of pressure drop between simulation and experimental tests

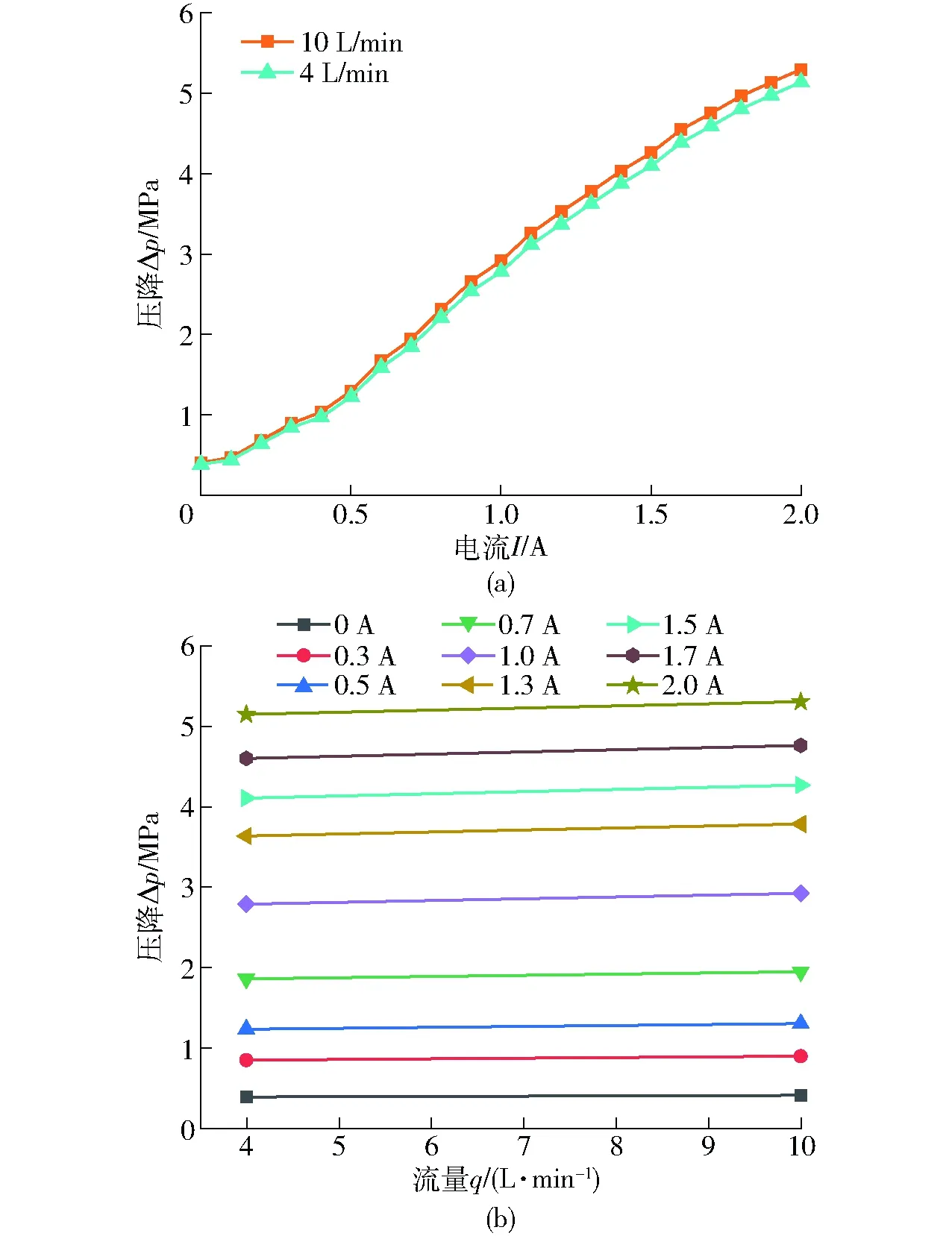
图14 流量变化条件下压降测试结果Fig.14 Comparison of pressure drop at different flow rates

图14a所示为系统流量分别为4、10 L/min时的压降变化。同样加载电流情况下，流量为4 L/min时测得的压降略小于流量为10 L/min时所测得的压降，而且在不同电流的状况下压降也稍有差异。电流为0.3 A时压降相差49.2 kPa，电流为1.0 A时压降相差约为132.8 kPa，造成这种压降差距的原因主要有：电动机运转时有振动、液压泵长期高强度运行损耗了齿轮、磁流变液回流时对油箱箱体产生冲击混进空气等。另外由图14b可看出，随着加载电流的增加，电流范围在0.7～1.3 A的压降曲线跃升较快，说明磁流变液的屈服应力增长较快，随后曲线之间距离逐渐减小。同一电流下，泵源流速改变，磁流变阀的压降会有一些改变，泵源流速越大，压降越大，然而这种变化较小。一定工况条件下，可忽略泵源流速的影响，证明了磁流变阀良好的工作性能。

图15为不同阻尼间隙下的压降变化关系。改变阻尼圆盘厚度，使得液流通道处的阻尼间隙分别为2、1 mm。加载电流0 A时，阻尼间隙为2 mm时压降为407 kPa，阻尼间隙为1 mm时压降为444 kPa；随着电流的增加，压降性能差异开始逐渐显现；加载电流为0.8 A时，阻尼间隙2 mm的磁流变阀压降为2.23 MPa，阻尼间隙1 mm的磁流变阀压降就高达5.32 MPa。这反映了阻尼间隙对压降性能的影响很大，在能产生磁流变效应的范围内，阻尼间隙越小，磁流变效应发挥越充分，但考虑到间隙太小会影响液体流动，造成流道堵塞，所以0.5～1.0 mm是磁流变效应的最佳范围。

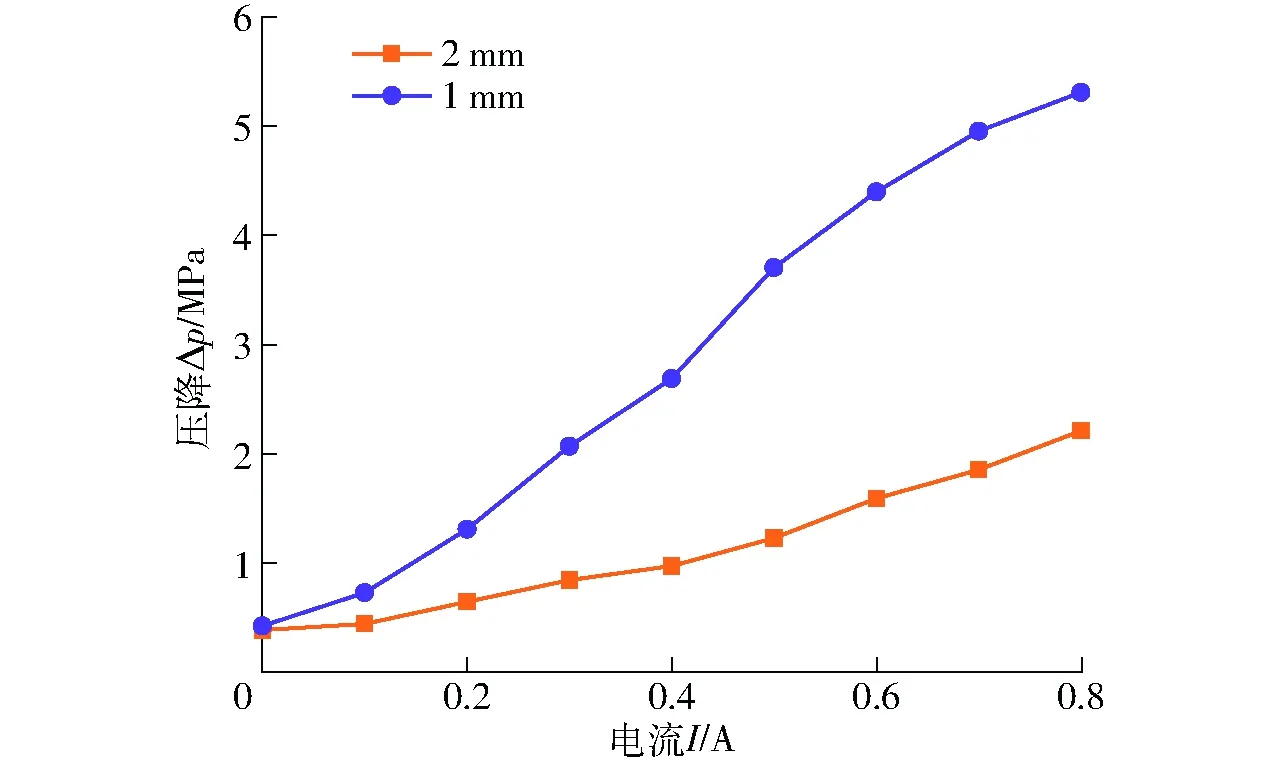
图15 不同阻尼间隙磁流变阀压降对比曲线Fig.15 Comparison of pressure drop under different damping gaps

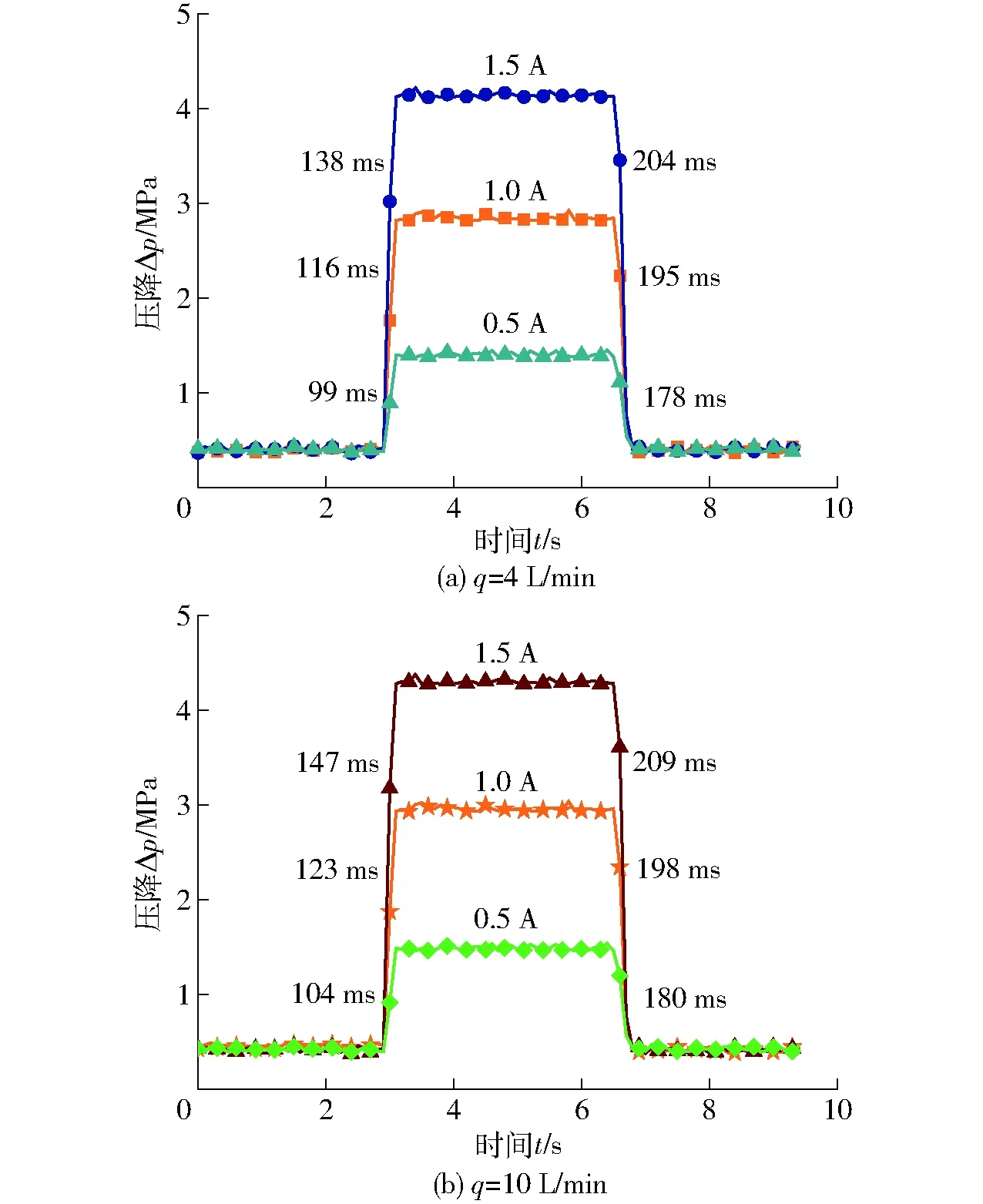
图16 输入电流变化下压降响应时间Fig.16 Voltage drop response time under current change

4.3 响应性能分析

测试时采集卡中每一个通道的采集点数设为100，采样频率为1 000。图16a为磁流变阀在负载工况1、系统流量4 L/min时不同加载电流下压力瞬态响应过程。随着电流的增加，压降大幅增加，上升阶段响应时间从0.5 A时的99 ms逐渐增至1.5 A时的138 ms；下降阶段响应时间从0.5 A时的178 ms逐渐增至1.5 A时的204 ms。

图16b所示为该磁流变阀在10 L/min流量下不同输入电流时压力瞬态响应过程。由于流量变大，能达到的压降会有少量提升，所以响应时间更长。可以观察到，随着电流增加，上升阶段响应时间从0.5 A时的104 ms逐渐增加到1.5 A时的147 ms；下降阶段响应时间从0.5 A时的180 ms逐渐增加到1.5 A时的209 ms。在未达到饱和前，上升阶段与下降阶段期间响应速度都与电流存在一定关系。随着电流的增加，达到该压降所耗费的时间响应也随之增加。总体来说，下降阶段响应时间大于上升阶段响应时间，主要原因除了齿轮泵高速运转后造成的延迟外，还包括电源切断后，线圈周围仍有少量的磁场没有消退。

5 结论

(1)设计了蚊香盘式液流通道磁流变阀，并推导其压降数学模型。电磁场仿真结果显示，2.0 A加载电流时，压降可达5.58 MPa。

(2)通过磁流变阀对不同外加电流下的压降特性进行实验测试，实验结果表明，电流为2.0 A时压降可达5.1 MPa，与仿真结果趋势一致。另外与现有外形尺寸相同的径向流磁流变阀(压降小于2.5 MPa)相比，压降增长率达100%。

(3)对磁流变阀的响应性能进行了测试分析，结果表明，所设计的磁流变阀响应迅速，上升阶段的响应时间比下降阶段的响应时间短，并且外加电流越大，响应时间越长。