车辆换挡系统调压阀优化设计与试验
魏列江 李 维 刘增光 罗小梅 安一超 项 可
(1.兰州理工大学能源与动力工程学院, 兰州 730050; 2.中国北方车辆研究所车辆传动重点实验室, 北京 100072)
0 引言
换挡系统作为车辆的关键组成部分,其性能直接影响车辆传动平稳性和乘坐舒适性[1]。通过接收相应的接合指令,换挡系统控制离合器充油[2-3]。在充油过程中,如果离合器内油压升高过快,会加剧离合器摩擦片的滑摩,产生剧烈的换挡冲击,从而降低摩擦片的使用寿命[4-5]。为了使充油过程尽量快速且平稳,需要改善车辆的换挡品质[6-9]。影响换挡品质的因素有换挡动作、离合器油压、车辆本身的惯性以及换挡规律等[10-12]。国内外主要通过液压缓冲阀、脉宽调制(PWM)高速开关阀和调压阀对离合器油压进行控制[13]。其中,液压缓冲阀控制简单、性能可靠、成本低廉,但在弹簧刚度和弹簧预紧力不变的情况下,难以满足不同挡位对离合器缓冲特性的要求[14];脉宽调制高速开关阀响应迅速、易于微机控制,但允许通过的流量较小,应用范围有限[15];调压阀的综合性能好,控制精度高,能适应恶劣的工作环境,其动静态特性可以满足大多数工业应用要求,是重型车辆控制元件的首选[16-19]。目前调压阀相关研究已经取得了一定的进展[20-22],但大多集中于单参数、单优化方案,而对于多参数、多优化方案的研究仍较少。考虑到充油压力曲线可以在一定程度上反映换挡过程中油压特性的变化规律,本文将以换挡系统充油压力作为优化目标,采用多种算法对调压阀进行多参数的优化设计,选出最优算法,确定调压阀最优结构参数,并加以试验验证,以期提高换挡系统的稳定性并改善换挡品质。
1 调压阀工作原理
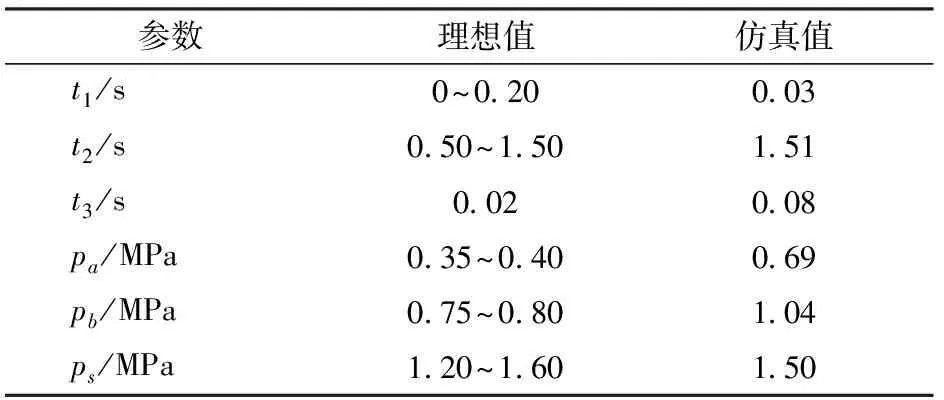
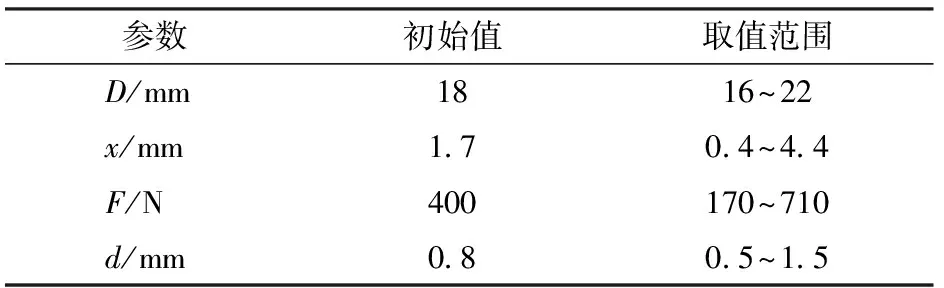
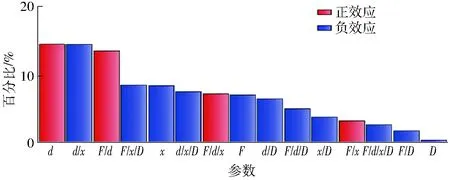
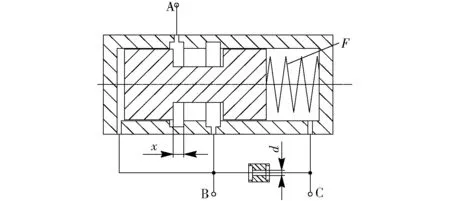
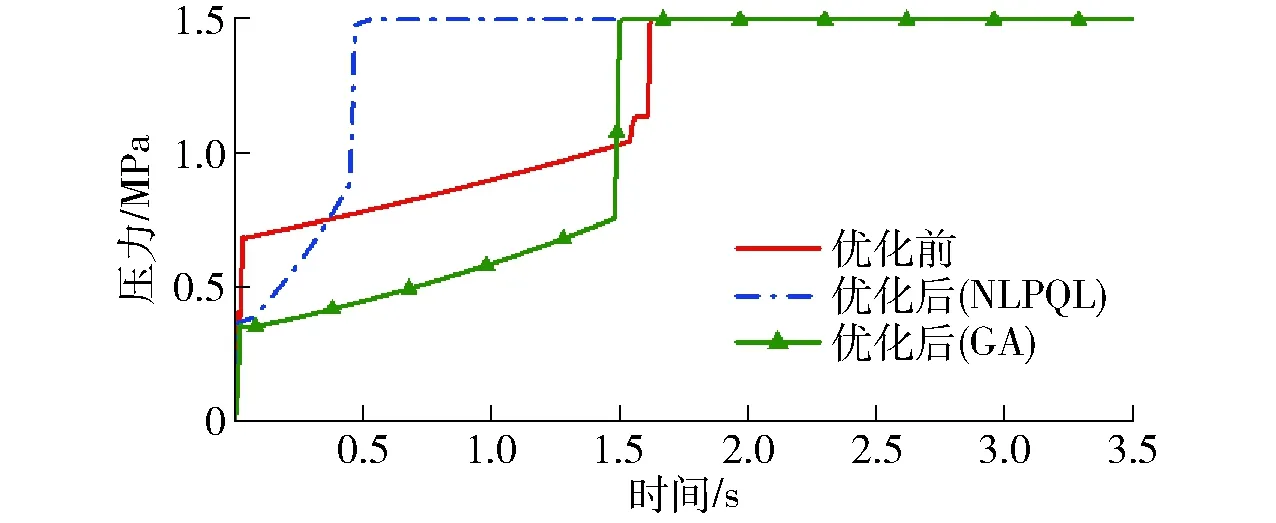
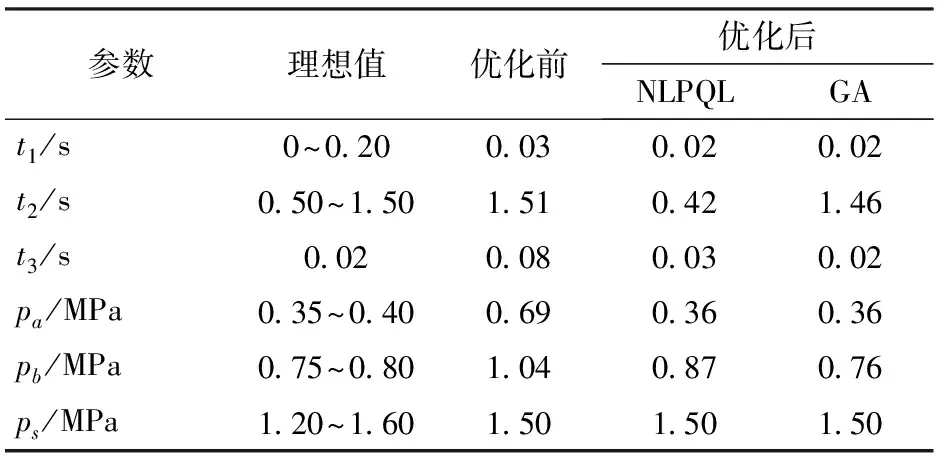
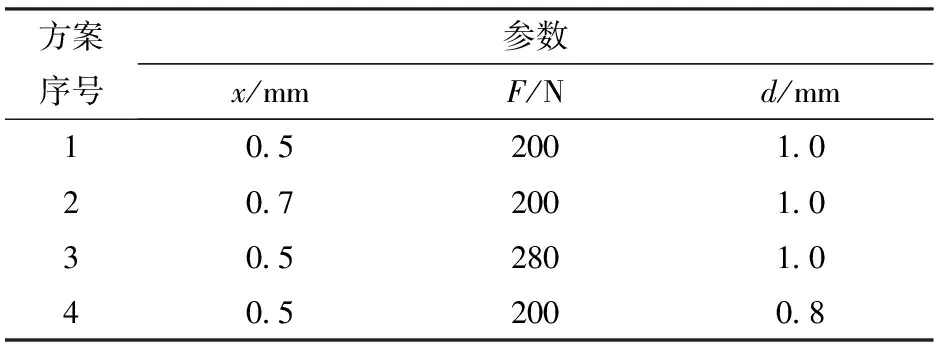
图1为调压阀原理图,由比例溢流阀作先导阀,减压阀作主阀构成。通过控制调压阀的输出压力,可以调节进入离合器的油压。其中,主阀进口压力为p1,出口压力为p2;先导阀进口压力为p3。当先导阀进口压力小于其设定压力时,先导阀关闭,主阀阀口为最大开度,不起减压作用,即主阀进出口压力相等(p1=p2);当先导阀进口压力大于其设定压力时,先导阀开启,主阀阀口开度减小,此时主阀的出口压力小于进口压力,其值约为先导阀进口压力(p3≈p2 图1 调压阀原理图Fig.1 Schematic of pressure regulating valve 在AMESim元件库中选择相应的元件进行连接,可得到换挡系统的AMESim仿真模型,如图2所示。供油单元的油液依次通过电磁换向阀和调压阀进入离合器。电磁换向阀控制充放油状态,调压阀调节充油压力,离合器进行换挡。表1为换挡系统AMESim模型的主要参数。 图2 换挡系统AMESim仿真模型Fig.2 AMESim simulation model of shift system 表1 换挡系统AMESim模型主要参数Tab.1 Main parameters in AMESim model of shift system 图3为理想充油曲线。根据离合器油缸内充油压力的变化情况,整个充油过程分为3个主要工作阶段[23]: (1)快速充油阶段(0~a段):油液进入离合器油腔,克服弹簧预紧力,消除间隙,直到摩擦片贴合为止。该阶段需要快速起步,以缩短时间,减小功率损失;压力由离合器贴合时分离弹簧的张力以及离合器油缸的承压面积来决定。 (2)缓冲升压阶段(a~b段):摩擦片刚贴合时,主动摩擦片转速较高,从动摩擦片转速较低,经过滑摩过程,最终同步运动。充油过程主要控制该阶段,要求必须确保油压的精确控制,从而减缓摩擦片的接合速度,降低滑摩扰动,实现平稳换挡。该阶段的时间不宜过短,压力由离合器传递的摩擦力矩来决定。 (3)阶跃升压阶段(b~c段):为了提高换挡效率,此阶段离合器的充油压力应快速升至系统压力,对换挡品质的影响极小。该阶段升压较快,耗时较短;压力由离合器传递的摩擦力矩来决定。 图3 理想充油曲线Fig.3 Curve of ideal oil filling 图3中,pa和pb分别为缓冲升压阶段的初始压力和终止压力,ps为系统压力;t1为快速充油时间,t2为缓冲升压时间,t3为阶跃升压时间。 如图4所示,设置运行时间为3.5 s,对充油过程进行仿真分析。快速充油阶段从0开始,经过0.03 s进入缓冲升压阶段,持续1.51 s后到达阶跃升压阶段,最终经过0.08 s后,充油压力稳定在1.50 MPa。其中,在缓冲升压阶段中,初始压力约为0.69 MPa,终止压力约为1.04 MPa。在阶跃升压阶段,出现了明显的压力波动。 图4 仿真充油曲线Fig.4 Curve of simulated oil filling 充油曲线参数理想值与仿真值的对比如表2所示,在仿真充油曲线中,符合理想充油曲线要求的参数较少,且充油过程应尽量避免压力波动的产生。 误差积分准则是期望值与实际值之间偏差的函数积分形式,可以用来衡量系统性能的优良程度[24]。采用误差积分准则所设计的系统,瞬态响应的振荡性小,对参数具有较好的选择性,其计算式为 (1) 表2 充油曲线参数的理想值与仿真值的对比Tab.2 Contrast between ideal and simulated values of parameters in oil filling curve 式中t——响应时间 e(t)——响应误差 针对调压阀的结构优化问题,将调压阀的输出油压p(t)作为优化目标,可得 (2) 式中p(T)——调压阀最终稳定时的输出压力 将式(2)代入式(1)可得 (3) 其中,J越小,响应时间和超调量越小,调压阀的性能越好,优化效果越好。故目标函数为 (4) 调压阀作为换挡系统的关键部件,可以对离合器的油压进行精确控制,从而提高换挡品质。调压阀主要参数取值范围如表3所示。 表3 调压阀主要参数取值范围Tab.3 Main parameters range of pressure regulating valve 图5为Pareto图,表示调压阀中相关参数对充油压力的影响程度。Pareto图既可以表示单参数对充油压力的影响程度(如D表示阀芯直径对充油压力的影响程度),也可以表示复合参数对充油压力的影响程度(如d/x表示在阻尼孔直径和阀口开度这两个参数的共同作用下,对充油压力的影响程度)。 图5 Pareto图Fig.5 Pareto chart 如图5所示,阀芯直径对充油压力的影响程度很小,可以忽略不计。阻尼孔直径、阀口开度和弹簧预紧力对充油压力的影响较大,故本文仅对这3个参数进行优化。图6为调压阀关键参数的结构示意图。 图6 调压阀结构图Fig.6 Structure chart of pressure regulating valve 边界约束g(X)可以表示为 (5) 故充油压力的目标函数为 minJ(x,F,d) (6) 工程问题的优化往往比较复杂,其设计变量和约束函数可能是线性或非线性、连续或离散的。为了提高参数辨识的速度和精度,本文采用两种算法对调压阀进行多参数的结构优化。二次拉格朗日非线性规划算法(NLPQL)可将约束条件线性化,通过二阶泰勒级数的方法展开目标函数,采用二次规划法得到新的点进行线性搜索,利用函数导数、梯度等数学方法,实现高效的优化[25]。遗传算法(GA)效仿生物进化过程中遗传繁殖的规律,对优化问题中的个体进行编码和优化 (如交叉、选择、变异等),通过迭代的方法从新种群中找出较优解或最优解的组合[26]。两组优化后调压阀的结构参数如表4所示。 在换挡系统AMESim模型中应用两组优化数据进行仿真,可得优化后的充油曲线,将其与优化前的曲线进行对比,如图7所示。由图7可知,在快速充油阶段,优化前后的时间基本一致;在缓冲升压阶段,优化后的时间和始末压力均有所降低, NLPQL耗时最短;在阶跃升压阶段,优化前后的充油压力最终稳定在1.50 MPa,优化后的充油压力达到稳定值的时间均减少,且优化后的压力波动消失。 表4 优化前后调压阀的关键参数Tab.4 Value of key parameters in pressure regulating valve before and after optimization 图7 优化前后充油曲线的对比Fig.7 Comparison of curves of oil filling before and after optimization 表5为充油曲线参数的理想值与优化值的对比。由表5可知,优化后充油过程的各项参数均得到一定程度的改善。NLPQL优化后充油曲线中只有部分参数符合理想充油曲线要求;而GA优化后各项参数均符合要求。故GA优化效果更好。 表5 充油曲线参数的理想值与优化值的对比Tab.5 Contrast between ideal value and optimized value in oil filling curve 图8为换挡系统的试验原理图。液压泵由电动机驱动旋转,从油箱中吸油,向电磁换向阀供油。溢流阀用来调定系统压力。电磁换向阀用来控制离合器的充放油状态。调压阀用来调节离合器的充油压力。其中,传感器用来采集离合器的油压,通过信号采集器传输到工控机。将工控机上采集到的信号进行运算处理后,通过控制器来控制调压阀,从而实现对充油压力的调节。 图9为系统试验装置图,通过操控平台可以测量和控制阀组,用于调节换挡过程中的充油压力。 图9 系统试验装置图Fig.9 Graph of systematic experiments1.操控平台 2.阀组 图10 仿真和试验对比曲线Fig.10 Contrasts between simulated and experimental curves 根据控制变量法所设计的试验方案如表6所示。表6中方案1为GA的参数。在方案1的基础上,方案2将阀口开度由0.5 mm调至0.7 mm,方案3将弹簧预紧力由200 N调至280 N,方案4将阻尼孔直径由1.0 mm调至0.8 mm。在每组试验方案中,除阀口开度、弹簧预紧力、阻尼孔直径这3个参数参照表6取值,其他参数均与优化前保持一致。 表6 试验方案Tab.6 Experimental scheme 根据表6的试验方案,分别进行4组试验,所得试验结果如图10所示。由于试验过程中受油液泄漏等影响,试验曲线存在一定的波动;但总体而言,各组试验曲线和仿真曲线的趋势基本一致,验证了仿真模型的正确性。方案1中,试验曲线与仿真曲线较为贴合,满足理想充油曲线的要求。以方案1为研究对象,分别对比分析方案2、3、4与方案1之间的差异,可知:方案2中,阀口开度的增加,导致缓冲升压阶段后期的压力明显偏离仿真曲线,缓冲升压阶段和阶跃升压阶段出现剧烈波动,压力稳定之前其超调量较大;方案3中,弹簧预紧力的增加,导致缓冲升压阶段的始末压力均升高,超出理想充油压力的取值范围;方案4中,阻尼孔直径的减小,导致充油时间增加,超出理想充油时间的取值范围。综上所述,遗传算法优化后的调压阀,所得的试验曲线 (方案1) 波动较少,各阶段的时间和压力均符合理想充油曲线的要求,进而提高了换挡系统充油过程的稳定性,改善了换挡品质,验证了优化设计的合理性。 (1)基于误差积分准则,分析了换挡充油过程的Pareto图,得到调压阀中影响充油压力的关键参数为阀口开度、弹簧预紧力及阻尼孔直径。 (2)采用二次拉格朗日非线性规划算法和遗传算法对调压阀的3个结构参数进行优化,对比分析优化后的仿真充油曲线与理想充油曲线可知,遗传算法为最优算法。经遗传算法优化后,调压阀的阀口开度约为0.5 mm,弹簧预紧力约为200 N,阻尼孔直径约为1.0 mm。 (3)根据控制变量法,对遗传算法优化后的换挡系统进行试验,由试验结果可知,优化后的调压阀能够提高换挡系统的稳定性,其充油过程更加符合理想充油过程,改善了换挡品质,验证了优化设计的可行性及合理性。
2 换挡系统仿真建模与分析
2.1 AMESim建模
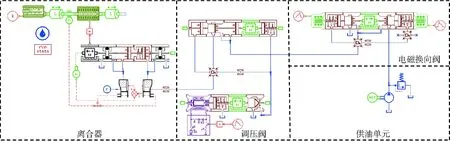

2.2 仿真充油曲线与理想充油曲线的对比
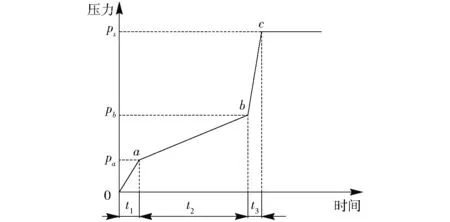
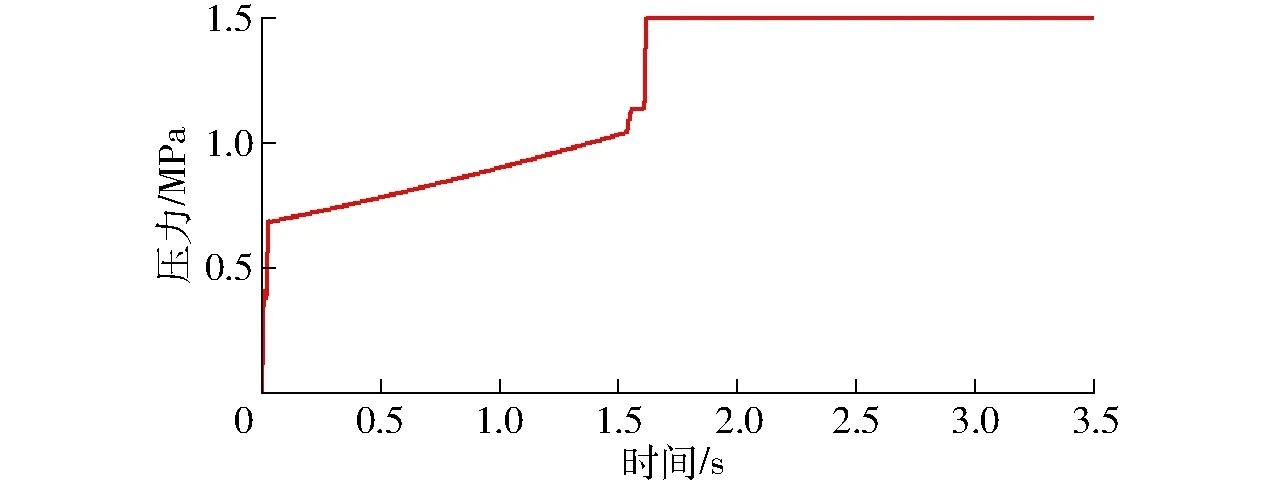
3 调压阀优化设计
3.1 目标函数
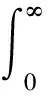
3.2 设计变量及边界约束
3.3 优化算法及其对比分析

4 换挡系统试验
4.1 试验原理


4.2 试验结果及分析
5 结论

