教学重、难点的教学应对：说课展示的关键——观摩青年教师圆周角定理说课有感

☉湖南省长沙市雅礼实验中学 刘 涛

最近观摩了一位青年教师（参加工作仅1年）模拟上课活动.这次模拟上课的展示是在“断网”（不与互联网连接的办公电脑）环境下独立备课1小时，然后模拟上课10～15分钟.其中一位青年教师可能没有教过九年级内容，对所给的圆周角教材（组织方复印了其中几页发给备课教师使用）全部实施了教学展示，使得模拟上课的时间超出3分钟.本文先梳理该课的主要教学环节，再跟进评析，并进一步给出笔者关于“圆周角（第1课时）”的教学建议.

一、青年教师的“圆周角（第1课时）”模拟上课记录

说明：青年教师将本课的流程设计成以下四个主要环节“基于情境，引出新知”“合作探究，丰富新知”“运用新知，变式讲评”“师生小结，课后训练”，流程清晰，学程推进富含节奏，这些都是值是肯定的，我们也按上述4个教学环节记录梳理.

教学环节（一）基于情境，引出新知

教师先让两名学生到黑板上画圆（如图1～3），并画出圆心角，然后在圆周上取点，再得到圆周角的概念（顶点在圆上，两边与圆相交的角叫作圆周角）.

图1

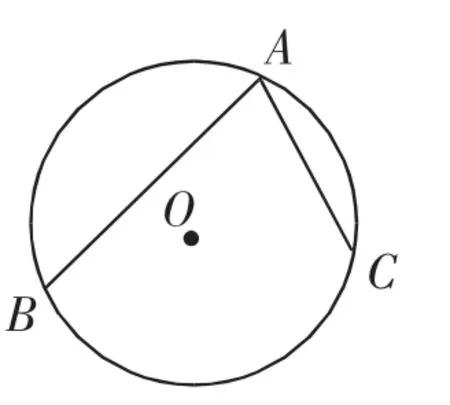
图2

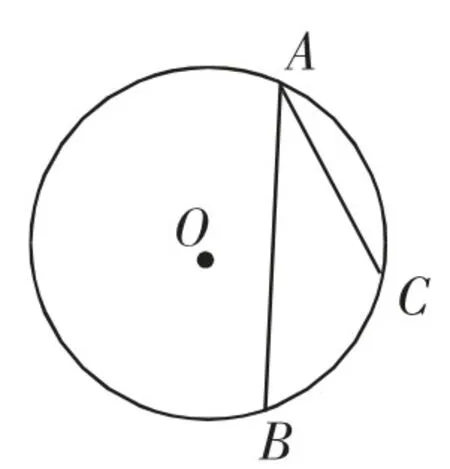
图3

接下来安排学生在练习本上度量并比较同弧所对的圆心角与圆周角的数量关系.如图2、图3，比较同弧所对圆周角∠BAC与圆心角∠BOC的大小关系.每名学生自己作图并量角后发现：同弧所对的圆周角的度数等于这条弧所对圆心角的度数的一半.

听课随感：这个环节以“数学现实”（学生画圆心角后再画出圆周角）引出新知，较为简洁，快速进入本课主题，值得学习.

教学环节（二）合作探究，丰富新知（分类讨论，证明定理）

在学生通过画图并度量发现圆周角的性质之后，安排学生在小组内讨论交流如何证明它们之间的数量关系，也就是由特殊到一般归纳证明圆周角定理.

教学组织：小组合作，比较组内成员各自图形是否有不同，找出顶点位置的可能位置，比如，圆周角与对应的圆心角有三种不同的位置关系，如图4～6.

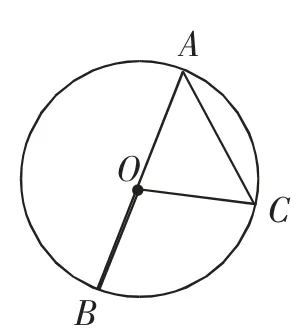
图4

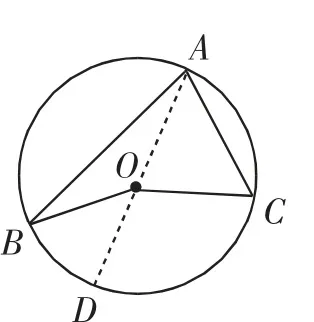
图5

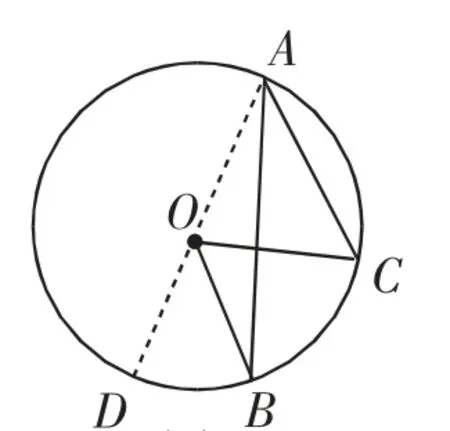
图6

教学组织：学生对图4容易直接根据三角形外角性质得出∠BOC=2∠BAC；而在图5中，作直线AD，也可利用三角形外角性质得出∠BOC=2∠BAC；在图6中，利用外角性质及求差的等式性质，可得∠BOC=2∠BAC.

听课随感：这个环节教师推进过快，对于圆周角的不同位置关系如何得到没有说清，说明教师在备课过程中对于圆周角教学难点的辨析仍然有待深入.

成果扩大：得到圆周角定理后，进一步得到以下推论，从一般走向特殊，教师很快引导学生得出“同圆中，同弧或等弧所对的圆周角相等”“半圆所对的圆周角是直角，90°的圆周角所对的弦是直角”.

听课随感：可能是模拟上课的时间紧张，教师在这个环节选择了一带而过，没有进行解读或停留，其实是一种教学展示的遗憾.因为圆周角定理一系列推论的教学应该是教学重点，不应该选择一带而过.

教学环节（三）运用新知，变式讲评

例1 如图7，图中是两个共斜边的直角三角形ABD和直角三角形ABC.

问题1：取AB的中点，连接CG、DG，分析它们的数量关系.

问题2：小智发现点A、B、C、D在同一个圆上.你觉得小智的发现有道理吗？说说你的理由.

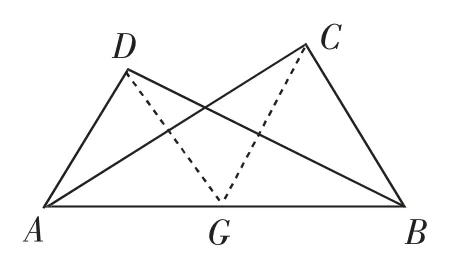
图7

听课随感：教师以两个递进式问题呈现这道例题的讲评，教师的意图可能是训练圆周角性质及推论的灵活运用.然而从这两个设问发现，训练的目标有些偏离本课教学目标，因为处理上述问题并不需要本课所学习的新知识，只是巩固了直角三角形斜边上的中线性质及圆的定义.这是选题不当的表现.

例2 如图8，点C、D在以AB为直径的圆上，∠ACB=90°，AC=6cm，AB=10cm，CD平分∠ACB.连接CD、AD、BD.判断△ABD的形状，并求出△ABD的面积.

图8

教学组织：教师先组织学生由勾股定理得CB=8cm，接着引导学生分析AD、BD如何求解，点D有何特殊位置关系，让学生发现点D是半圆弧的中点，为进一步发现等腰直角三角形ABD提供了铺垫.

听课随感：这道考题是教材上的经典习题，教师进行了教学展示，但具体细节如何处理并没有深入展开，也许因为时间原因，教师快速推进之后，竟然又从这道例题出发，过渡到了圆的内接四边形的概念和性质.

教学环节（四）师生小结，课后训练.

教师抓紧模拟上课的最后1分钟，在黑板上进行板书梳理，形成两条知识主线.一条主线是：圆周角——概念，相关概念，定理，分类讨论，边上、内部、外部，推论.还有一条主线是：圆内接多边形——概念，相关概念，圆内接四边形性质.

听课随感：这个小结看似进行了知识梳理，完善了板书，但是板书呈现的上述内容之间的逻辑性不强，有些零乱.

评课概述：虽然教学环节是清晰的，各个教学过程都“面面俱到”地呈现了，但是这节课主要不足在于课时划分不合理，最多只能到例题结束，后面的圆的内接四边形不宜出现.这也是没有教过该内容的新教师一个显著不足，即对课时划分没有感觉.

二、关于圆周角定理的教学思考

1.想清辨明圆周角定理的教学重点与难点

圆周角定理是基于圆的对称性展开研究的，具体来说，圆的轴对称性质带来了垂径定理，圆的旋转不变性带来了“圆心角、弧、弦、弦心距”之间的关系，进一步在圆心角学习之后引出圆周角.理解这点之后，就知道圆周角新课教学的数学现实就可以画圆，标出某段弧所对的圆心角，然后变化顶点得到圆内角、圆周角、圆外角，由于圆周角比较特殊，所以可以考虑深入研究圆周角的相关性质，这就是这节课的教学重点，而难点在于圆周角与圆心角的不同位置关系，需要安排学生充分讨论，把三种不同的位置都“穷尽”，然后确认同弧所对圆周角与圆心角之间的数量关系.在确定教学重点和教学难点之后，要预设必要的教学环节巩固重点并化解难点，这样就会深入思考这节课的教学目标与教学进度，而不是将教材上圆周角一节中的所有内容都在一节课中呈现出来.

2.恰当选取典型例、习题并跟进变式与追问

数学概念或定理的教学，往往需要安排例、习题的训练与讲评，用以巩固新知，体现所学新知的价值与运用.这时要特别重视教材上例、习题的功能与价值，因为编写教材的专家挑选习题都是精心为之，并不是随意选用，深入解读并挖掘教材例、习题的功能是教师必修的基本功.有些教师在新课教授时随意引用所谓全国各地“最新”中考真题，似乎体现时效性和关注中考的教学研究追求，实际上是本末倒置，因为有些中考真题虽然外形上考查的是本课的内容，但是还综合了其他一些章节的相关知识点，这时盲目选用到新课进行训练，就会出现内容效度不精准的问题.当然，教师针对学情结合教材例、习题进行一些调整、优化也是必要的，比如上文例2就很方便地得到一些变式与拓展（求弦CD的长，求四边形ABCD的面积，等等），供优秀学生挑战研习.