基于“三个理解”的“等腰三角形复习”教学设计

☉广东省冯大学名师工作室 ☉广东省深圳市民治中学 余 涛

《义务教育数学课程标准（2011年版）》提出“数学活动经验的积累是提高学生数学素养的重要标志”.要让学生学习生长的数学、动态的数学.使学生将学过的知识通过生长、类比迁移到当下学习的知识，发展数学能力，培养数学思维，并有所收获，那么教学设计就显得尤为重要了.

好的教学设计能让课堂充满生命力，能让学生从“学会数学的思维”向“通过数学学会思维”转变.所以教学设计应该从章建跃博士提出的“三个理解”，即理解数学、理解学生、理解教学出发.

一、“三个理解”理念下的北师大版八年级下册“等腰三角形复习”的教学价值

夸美纽斯说过“找到一种教育方法，使教师因此可以少教，但学生可以多学”.具有生长力的教学设计能使课堂充满活力，使教师和学生一起生长，一起发展.真正让学生把握数学的本质，提炼数学思想和方法，这样的数学才有价值.

（一）理解数学，教学设计要体现数学的系统性

理解数学指通过数学教学，让学生理解数学系统，即懂得学习的知识从哪里来，要到哪里去及怎么去的问题.同时除了知识，还包括数学眼光、意识、思维、方法、文化等数学整体素养.

“等腰三角形”在北师大版教材七年级下册第三章“认识三角形”、第五章“生活中的轴对称”中均涉及简单的知识.八年级下册第一章“证明（二）”系统学习了等腰三角形的概念、性质、判定及相关计算.九年级上册第一章“特殊平行四边形”中还要用到等腰三角形的相关性质和判定，知识相对分散.让学生感受知识生长的过程，将零散的知识变成系统性的知识，进一步体验数形结合，并渗透存在性问题的思考方法和解题路径是这节复习课价值所在.

本节课不过多追求题型的丰富，而是用6个问题搭建系统.回忆概念性质、构成等腰三角形、在直角坐标系中构成特殊等腰三角形和一般等腰三角形点的坐标等.设计的问题环环相扣，用一个图的多次改变让学生感受到知识系统的延展.用类比的数学思想让学生发现新、旧知识之间的通性，并总结规律和方法.让学生体验数学知识的系统性，形成数学知识的“生长”.

（二）理解学生，教学设计要基于学生的认知基础

理解学生意味着教学设计要从学生的认知出发，不仅解决当下的问题，更要着眼于学生的长远发展.要着力挖掘出数学所蕴含资源的价值，设计出具有生长力的数学，使学生在原有的认知基础上达到数学生长，发展数学能力.

“等腰三角形复习”这节课学生的认知基础是等腰三角形的概念和性质，即“两条边相等的三角形为等腰三角形”“等腰三角形两腰相等”.随着课堂的深入，之后的所有问题都以这两点为基本的认知起点.每一个新问题都是在原有问题上进行螺旋式的提高，新、旧问题共同搭建了等腰三角形的知识系统，同时建立了与其他知识的联系.引入中的概念和性质回顾，知识构建中的一图多变而万变不离其宗的探索，再到从一般到特殊再从特殊到一般的方法归纳，所有解决问题的思想都是分类讨论.这样的设计联系前后，贯通上下，让新知识在原有知识的基础上生长，潜移默化地在学生心中种下数学的种子，并培养学生类比、迁移等数学思想，让学生理解数学本质.

（三）理解教学，教学设计符合教学的生长规律

通过6个层层递进的问题，将本来看似孤立的知识巧妙联系在一起，将复杂的问题分解成学生可以处理的若干个问题，使得学生的关键能力因为课堂教学的转变而得到提升，符合学生的学习规律，也符合课堂知识的生长规律.

从构成等腰三角形的点到组成等腰三角形的边；从点的位置到点的个数，再到点的坐标；从一般的等腰三角形变化为等腰直角三角形，再从等腰直角三角形回到一般的等腰三角形，每一个问题的提出都让学生在教学中生长，让学生通过不断的变化来厘清数学中不变的规律.这也是教学生长最后需要落脚的地方.

二、“三个理解”教学价值指引下的“等腰三角形复习”教学设计

（一）情境引入

问题1：什么是等腰三角形？等腰三角形的性质有哪些？

问题2：如图1，能否找一点C，使得△ABC是等腰三角形？（结论见图2）

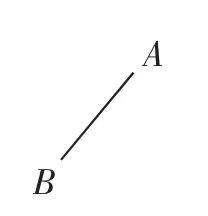
图1

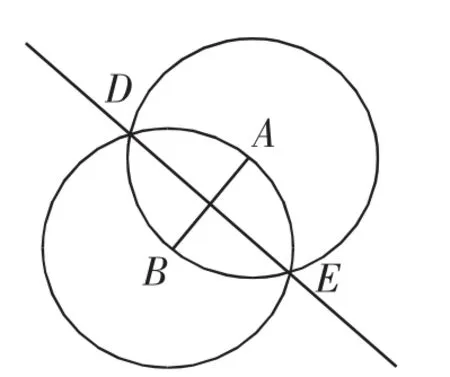
图2

设计意图：从引入开始，就让学生探索，这需要学生进行适当的分类讨论.从这个阶段就开始训练用严谨、简洁的数学语言来描述自己的想法.简洁的叙述就是分别以AB为底和以AB为腰的等腰三角形.从而达到规范学生几何语言的使用.

（二）知识构建

问题3：如图3，在平面直角坐标系中，已知点A（1，1），点P是x轴上一动点.若△POA是等腰三角形，直接写出符合条件的点P的坐标.（结论见图4）

图3

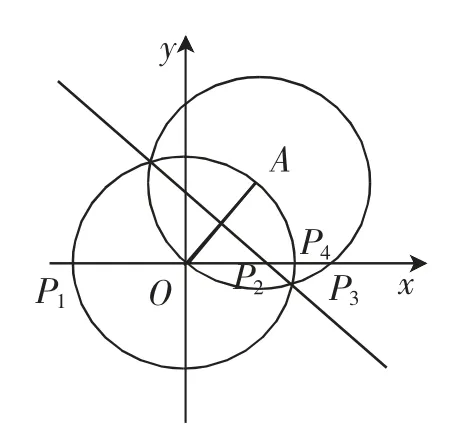
图4

问题4：如图5，将图3中的线段AB向左平移1个单位，点P在x轴上，是否存在点P，使△PAB为等腰三角形？若存在，请求出点P的坐标.（结论见图6）

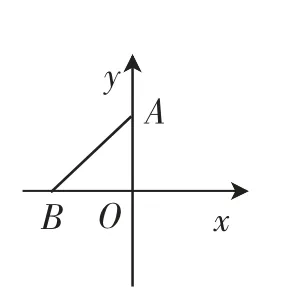
图5

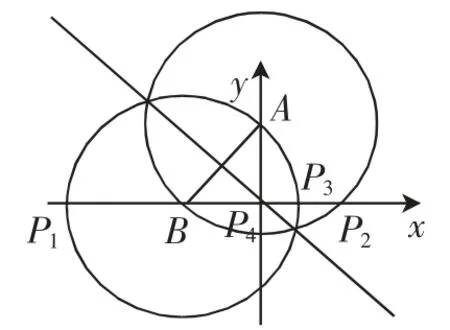
图6

问题5：如图7，平面直角坐标系中，点A（0，2）、B（-4，0），点P在x轴上，是否存在点P，使△PAB为等腰三角形？若存在，请求出点P的坐标.（结论见图8）

图7

图8

问题6：如图9，点A（-1，3）、B（-5，1），点P在x轴上，是否存在点P，使△PAB为等腰三角形？若存在，请求出点P的坐标.（结论见图10）

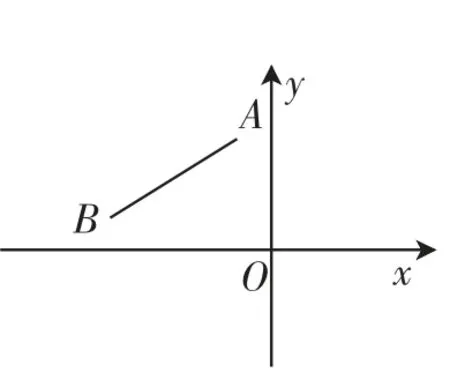
图9

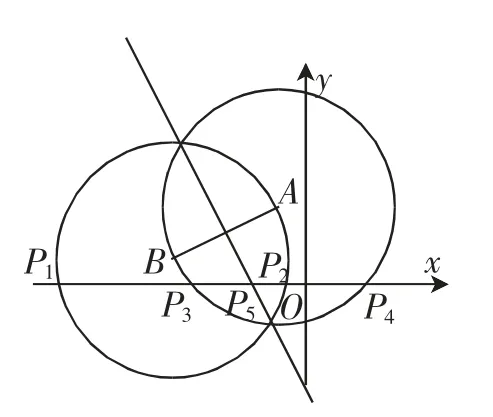
图10

（三）综合讨论

如图11，在平面直角坐标系中，正方形ABCD的顶点A在y轴的正半轴上，顶点B在x轴的正半轴上，OA=4，OB=3.

（1）求点D的坐标.

（2）求直线BC的解析式.

（3）在直线BC的上是否存在点P，使△PCD为等腰三角形？若存在，请求出P的坐标；若不存在，说明理由.

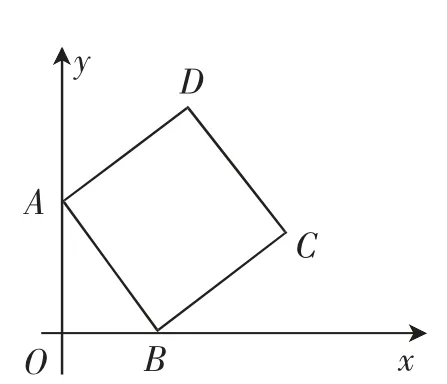
图11

设计意图：等腰三角形的存在性是一个经典的数学问题.让学生先从图形及性质扎根，通过对知识的回忆，让不同层次的学生都有一种学习的体验，有助于提升学生的学习智慧，拓展学生的思路.通过问题设置和一图多变，一方面，引导学生感受图形“变中不变”的魅力，领悟其数学本质；另一方面，训练学生用规范的几何语言，有条理地表述提出和解决问题的过程.同时渗透数学分类思想，引入坐标系让教学自然而然生长到数形结合的方面，并且此类问题让学生形成用圆规画圆来解决等腰三角形（菱形）存在性问题的套路.

（四）回顾总结

问题7：请同学们回忆一下，本节课你学到了哪些知识？我们解决几何问题的基本思路是什么？

设计意图：目的是让学生回头想一想，对照着黑板上的图形变化，说出自己对本节课的感悟.如果有必要，教师需主动干预，帮助学生总结研究几何问题的基本套路.再次强化学生“概念—判定—性质—应用”的研究套路，以及分类讨论的研究方法.

三、“三个理解”下教学设计背后的思考

（一）强调图感，寻得规律，建立系统

因为学生在几何学习过程中常常缺乏感性的识图和理性的分析，所以数学教师在进行教学设计时必须建立在学生学习生长规律之上.本节复习课探索等腰三角形存在性问题，从一般的等腰三角形变化为特殊的等腰直角三角形，再从特殊的等腰直角三角形回到一般的等腰三角形.一个图的变化，让学生通过不断变化来厘清数学中不变的规律，形成系统的数学知识架构.这也是教学生长的落脚点.

（二）有章可循，构建生长的路径

教师的教学能力体现在两个方面：一是将复杂的问题简单化，二是将简单的问题深刻化.本节课7个环环相扣的问题提出，让学生逐渐递进直到难点突破.巩固和加强学生对等腰三角形性质的运用和对存在性问题的解决思路的理解.同时一图到底既增强了学生的应变能力，又使课堂充满趣味和生机.

四、结语

哲学思想认为世间万物发展规律和框架，即为“体”；通过思考形成解决事情的方向或者方法，即为“术”；用确定的方向或方法根据实际情况来解决问题，即为“用”.“体、术、用”三位一体，构成解决实际问题的完整过程.

理解数学、理解学生、理解教学即为数学教学中的“体、术、用”.

“体”是根本.万变不离其宗，这将教师对数学的理解提升到整个教学的最高地位.如果教师连数学都不理解，何谈教学？又何谈教学设计？

“术”是方法.没有放之四海而皆准的唯一教学设计和策略.这说明了数学教学要根据不同学情采取不同的应对策略.

“用”是操作.即使同样的课也会面临不同的学生，各种方法的使用都不能墨守成规.要将对数学的理解、对学生的理解、对内容的设计转化为教师每堂课上灵活的应对.

教学设计需要教师让书本上的数学知识活起来、生长起来.把数学的关键能力具体变成“教化”的过程.外在“教”的层面是把数学知识传授给学生，这个是“授业”的作用；内在“化”的层面指教学中要对学生进行数学眼光、意识、思维、方法、文化等数学能力的培养和提升，这是“传道”的过程.只有两者在教学过程中统一，才是数学课堂教学的价值所在.