七沟道球笼式等速万向节磨损及仿真分析*

谢 鲲，刘征宇，郭常宁，闫公哲，石宝枢

（1.上海应用技术大学轨道交通学院，上海 201418； 2.上海交通大学机械与动力工程学院，上海 201400；3.华东理工大学机械与动力工程学院，上海 200237； 4.浙江众达传动股份有限公司，金华 321025）

前言

球笼式等速万向节可以实现输入轴和输出轴存在夹角时的等角速度传动，其载荷是星形套端输入轴通过星形套内沟道椭圆曲面传递给钢球球面，再由钢球球面传递给钟形壳外沟道椭圆曲面，而到达钟形壳端输出轴的转矩和回转运动。钢球、星形套、保持架、钟形壳这几个主要部件的受力过程是输入转矩传递的关键，钢球与星形套、保持架、钟形壳在传递转矩过程中的法向接触力、摩擦力可作为球笼式等速万向节部件间的磨损量和疲劳寿命的理论依据。

目前国内外对于球笼式等速万向节的内部受力及摩擦磨损的研究并不多见。文献［1］中通过三维重构技术搭建了球笼式等速万向节的三维模型，并对其承受极限转矩时的内部接触应力进行有限元分析，最后对比两种极限工况的数值解；文献［2］中通过对七沟道球笼式等速万向节星形套和钟形壳圆弧形沟道曲率的解析，根据Hertz接触理论分别计算出沟道与钢球接触时的接触应力，进而探讨该类万向节优化设计的规律；文献［3］中对球笼式万向节内外滚道接触应力进行了有限元分析，得出内滚道的接触应力明显大于外滚道，内滚道更容易受到破坏。但是，钢球在传递运动和转矩的过程中产生的摩擦力，以及由摩擦力产生的轴向窜动力、径向力、偏转转矩却很少有人研究，这些力的变化会直接影响万向节的磨损-疲劳寿命，而且其研究结果将对以后研究分析万向节内部的摩擦磨损有着非常重要的理论指导意义。

鉴于此，本文中通过钢球在沟道内的瞬时角速度和星形套内沟道钟形壳、外沟道与钢球接触点的瞬时角速度，计算钢球在沟道内的瞬时滑滚比，以此判断钢球在沟道内的滑滚移动状态，从而计算并分析钢球与星形套、钢球与保持架的摩擦力，得到了摩擦力随着输入端角速度、输入端对输出端摆角的变化规律，同时根据Archard磨损理论，对球笼式等速万向节进行磨损分析。

1 受力模型

图1为钢球在万向节内的受力模型。由图可知球笼式等速万向节一个钢球在一组星形套内沟道、钟形壳外沟道和保持架窗口作用下的受力情况。钢球的球心O及其所在坐标系ρQ＝［］；当星形套端输入轴IN与钟形壳端输出轴IW之间的轴间摆角为2θ时，作为星形套和钟形壳之间传递动力的关键部件，钢球收到星形套内滚道和钟形壳外滚道的周向力作用，此力使钢球把星形套内滚道传递的动力带给钟形壳外滚道；钢球与星形套和钟形壳接触点分别为N和W，在此两点钢球的法向接触力分别为QNQi和QWQi，有此两个法向接触力而产生的摩擦力分别为fNQi和fWQi。除了与星形套内滚道和钟形壳外滚道接触以外，钢球还始终与保持架相接触，在保持架窗口的上下面分别对钢球有法向接触力QJQi以及由此法向接触力产生的摩擦力fJQi。球笼式等速万向节在其运动过程中，各个钢球的瞬时受力，不论是法向接触力 QNQi（QWQi），QJQi或是摩擦力 fNQi（fWQi），fJQi，都不是一成不变的，而是随着转角δ和星形套端输入轴IN与钟形壳端输出轴IW之间的轴间摆角2θ的变化而不断改变的。

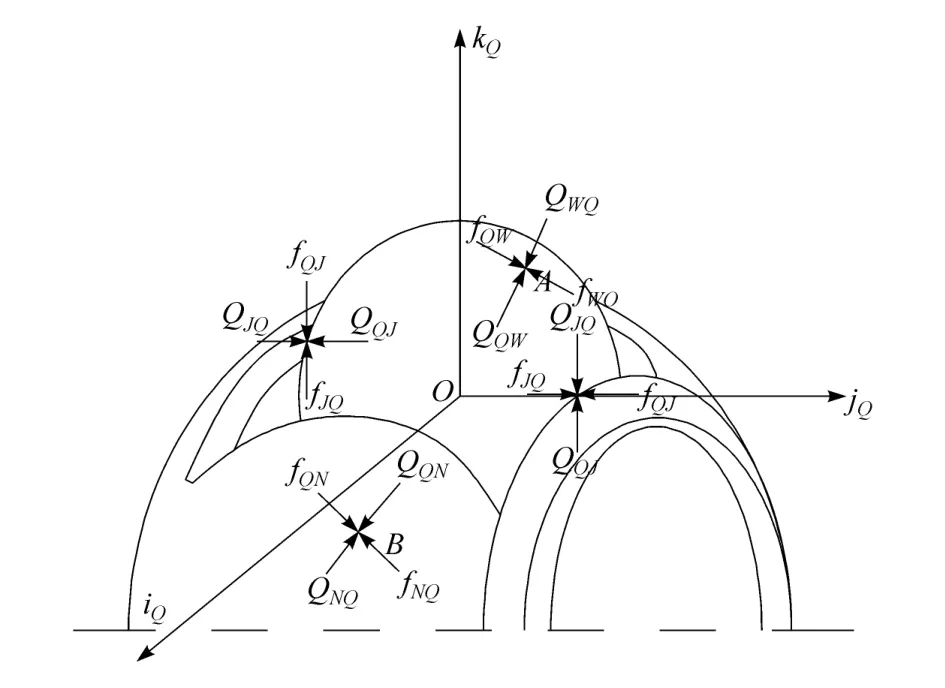
图1 钢球受力模型

2 滑滚比S的数学模型

在球笼式等速万向节的星形套端输入轴IN旋转一周的过程中，各个钢球在星形套内沟道和钟形壳外沟道内做纯滑动、纯滚动或者滑滚结合的运动，借助滑滚比可以明确钢球在沟道内的具体运动形式。滑滚比是指在工程应用当中，零件滑动摩擦与滚动摩擦的比值，滑滚比S为

式中：v1为接触部件1在接触点处的瞬时线速度；v2为接触部件2在接触点处的瞬时线速度。若求得的S＝0，则两部件在接触时做纯滚动运动，若求得的S＝2，则两部件在接触时做纯滑动运动，若S∈（0，2），则两部件在接触时做滑滚结合运动。

钢球中心OQ的旋转角速度ωQ［2］为

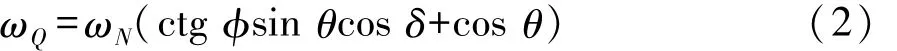
由式（1）和式（2）可得出钢球与星形套（或者钟形壳）的滑滚比计算公式，并可以此作为判断钢球在星形套内沟道和钟形壳外沟道内的摩擦为何种形式。

在球笼式等速万向节中：

由式（3）和式（4），可得滑滚比 S为

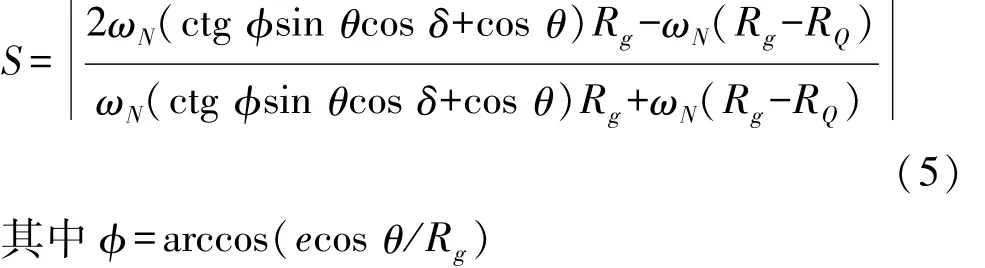
图2为滑滚比S随转角δ和轴间摆角2θ的变化规律。当钢球与星形套内沟道和钟形壳外沟道曲面的接触角α＝45°时（后面的讨论都基于该条件），滑滚比S与转角δ和轴间摆角2θ的函数关系曲线。由图2可知，滑滚比S随着转角δ在一个周期的旋转内呈周期性变化，随着轴间摆角2θ的增大而减小，并始终满足S∈（0，2），可以判断钢球在星形套内沟道和钟形壳外沟道内做着滚滑结合的摩擦运动。轴间摆角越大，滚动摩擦占到的比重越大，滑动摩擦占到的比重越小，轴间摆角为0°～35°的过程中，滚动摩擦与滑动摩擦的比下降，说明轴间摆角越大，钢球在星形套内沟道和钟形壳外沟道内运动过程中的滑移越少；轴间摆角为0°时，钢球在沟道内的位置始终相对保持不变，因此滑滚比也保持不变；轴间摆角为35°时，滑滚比随着钢球的往复运动而呈周期性变化［4-5］。

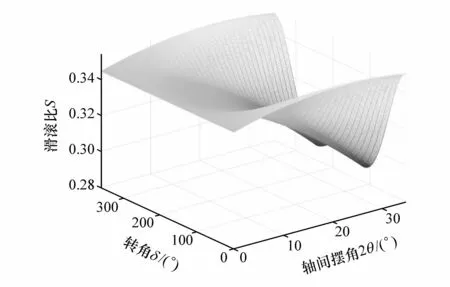
图2 滑滚比S随转角δ和轴间摆角2θ的变化规律

图3 为轴间摆角为35°时，滑滚比S随钢球与最外端距离L的变化规律。由图3可知，钢球运动到最外端时其滑滚比最大，运动到最内端时其滑滚比最小，滑滚比大的位置也是相对最容易出现磨损甚至是失效的位置。

图4为轴间摆角2θ为35°时滑滚比随转角和偏心距的变化规律。由图4可知，偏心距越大滑滚比也越大，在设计过程中选择合适的偏心距对球笼式等速万向节的性能也起到较大的影响。

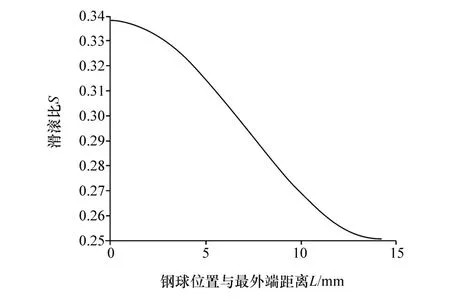
图3 滑滚比S随转角δ（沟道各位置）的变化规律

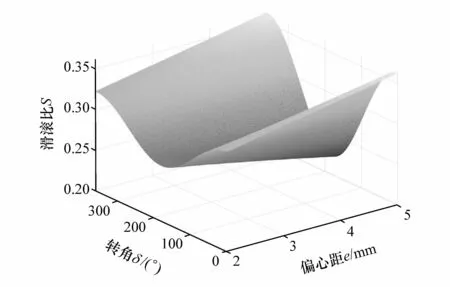
图4 轴间摆角2θ为35°时滑滚比随转角和偏心距的变化规律

3 钢球与星形套内沟道之间的摩擦力

由滑滚比S始终满足S∈（0，2）的计算结果，得出钢球在星形套内沟道和钟形壳外沟道内做着滚滑结合的摩擦运动的结论，可借此进一步计算球笼式等速万向节的摩擦力。在球笼式等速万向节的运动过程中，各个钢球随着转角δ的变化在星形套内沟道和钟形壳外沟道内往复运动，并保持始终处在同一水平面上。钢球运动时由于运动方向的改变，会导致钢球所受到的摩擦力方向发生变化，即在运动的一个周期内，摩擦力的值将有正负的变化。钢球在沟道内所受到的摩擦力为滑动摩擦力和滚动摩擦力，这两者分别为

式中：Fh为钢球在沟道内运动过程中所受到滑动摩擦力；Fg为钢球在沟道内运动过程中所受到的滚动摩擦力；μh为钢球在沟道内运动过程中所受到的滑动摩擦因数；μg为钢球在沟道内运动过程中所受到的滚动摩擦因数，在存在润滑的条件下，取 μh＝0.05，μg＝0.005；QNQ为钢球在沟道内运动过程中所受到的法向接触力；sign为特定函数符号，包含的值为钢球在沟道内往复运动时正负的判别条件，即当sin x＞0时，sign（sin x）＝1，反之当 sin x＜0时，sign（sin x）＝-1。将 QNQ的表达式代入摩擦力 FNQ中，得

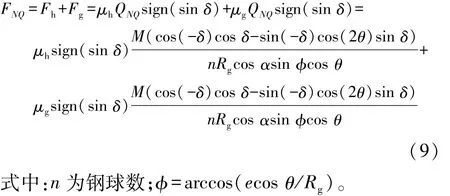
图5和图6分别为七沟道和六沟道球笼式等速万向节钢球在沟道内所受到的摩擦力FNQ与转角δ和轴间摆角2θ的关系曲线。由图可知：钢球在沟道内所受到的摩擦力FNQ在星形套端输入轴IN旋转一周的过程中，随着转角δ的变化呈周期性变化，并在转角为180°时发生方向的改变，从正值变为负值，因为钢球的运动方向发生了改变；当转角 δ为0°，180°，360°时，钢球处在最外端和最内端，其所受到的摩擦力绝对值最大；当转角δ为90°，270°时，钢球处在中间位置，其所受到的摩擦力绝对值最小；随着轴间摆角2θ的增大而增大，摆角从0°到35°的过程中，钢球所受到的摩擦力FNQ绝对值分别增加了近10 N，增长幅度约为17%；轴间摆角为0°时，摩擦力不变；轴间摆角为35°时，最大与最小法向摩擦力绝对值差值可达近20 N。七沟道球笼式等速万向节所受到的摩擦力在任意的轴间摆角下均小于传统的六沟道球笼式等速万向节，小载荷意味着同等材料和工况条件下能够获得更长的使用寿命［6-8］。

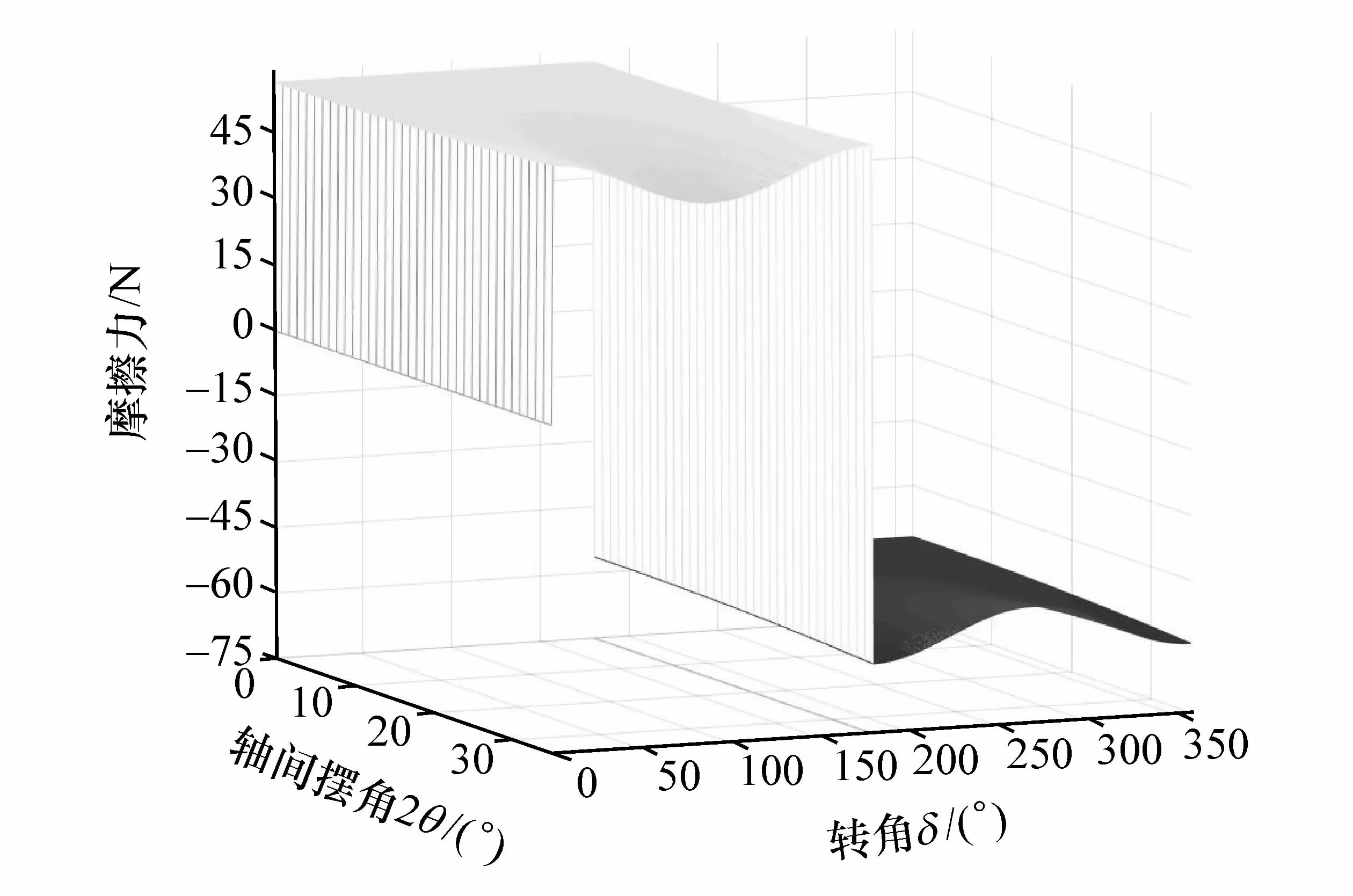
图5 七沟道万向节的变化规律

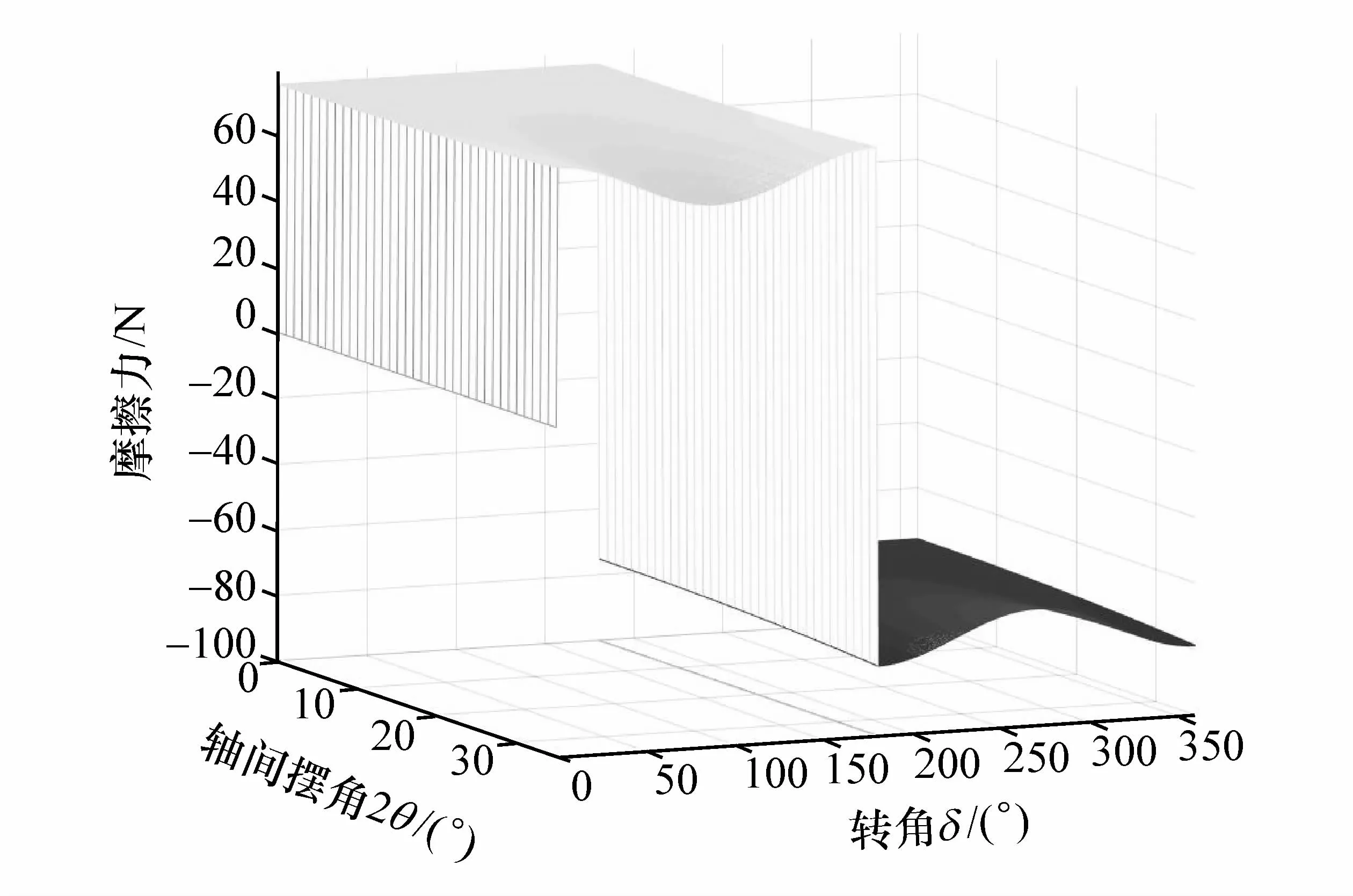
图6 六沟道万向节的变化规律

4 钢球与保持架之间的摩擦力

由于保持架的窗口允许钢球能够在垂直于星形套输入轴的平面方向上有移动，即在球笼式等速万向节的运动过程中，由于轴间摆角2θ的不断变化，钢球也会在保持架窗口内运动。运动过程中，钢球与保持架窗口上下表面接触，其所受到的摩擦力包括滑动摩擦力和滚动摩擦力，可分别表示为

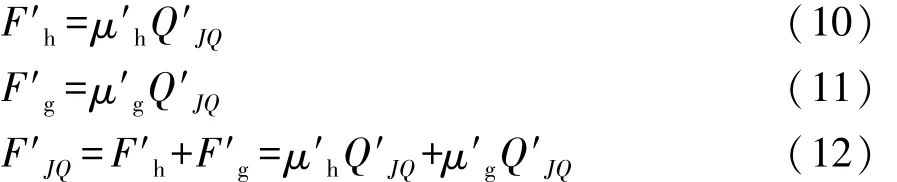
式中：F′h为钢球在保持架窗口内运动过程中所受到滑动摩擦力；F′g为钢球在保持架窗口内运动过程中所受到的滚动摩擦力；μ′h为钢球在保持架窗口内运动过程中所受到的滑动摩擦力摩擦因数；μ′g为钢球在保持架窗口内运动过程中所受到的滚动摩擦力摩擦因数，在存在润滑的条件下，取 μ′h＝0.05，μ′g＝0.005；Q′JQ为钢球在保持架窗口内运动过程中所受到的法向接触力。将Q′JQ的表达式带入摩擦力F′JQ中，得七沟道球笼式等速万向节：

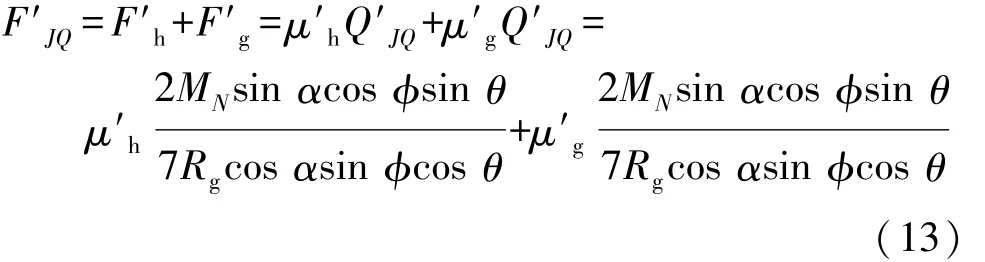
六沟道球笼式等速万向节：

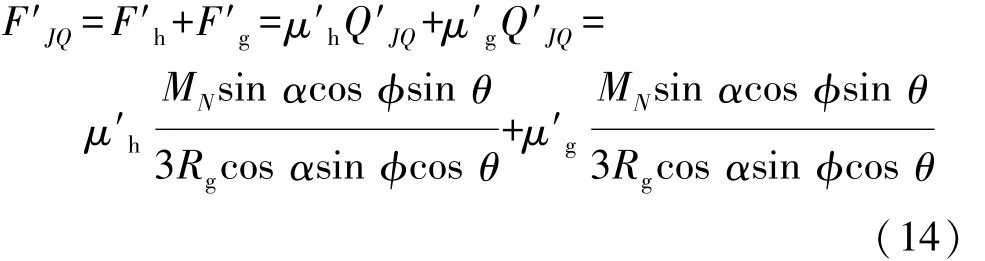
其中 φ＝arccos（e cosθ/Rg）

图7为钢球与保持架窗口摩擦力随轴间摆角2θ的变化规律。由图可知，球笼式等速万向节钢球在保持架窗口内所受到的摩擦力FJQ随着轴间摆角2θ的增大呈正比例函数增大，但在轴间摆角从0°到35°的变化范围内，摩擦力FJQ的变化只有不到5 N，该摩擦力的大小与前面讨论过的法向接触力和摩擦力有着较大数量级差别，对于球笼式等速万向节的运动影响极小，并不是影响使用寿命等的主要因素，但仍可发现七沟道球笼式等速万向节所受到的摩擦力在任意轴间摆角下均小于六沟道的，亦可证明其结构的优越性。

图7 钢球与保持架窗口摩擦力随轴间摆角2θ的变化规律

5 球笼式等速万向节的磨损分析

磨损率是两零部件接触发生摩擦过程中的一个重要基本量，本研究中分析的磨损率仅为在稳定磨损期的磨损率，影响磨损率的因素除了材料本身的特性之外，也与作用在接触表面的载荷有关。球笼式等速万向节因钢球与星形套内沟道和钟形壳外沟道的法向接触力关系，确定了其磨损类型为疲劳磨损。一直以来，广泛应用的计算接触物体疲劳磨损的磨损率主要应用的都是Archard磨损理论模型，其数学表达式为

式中：V为磨损量；K为磨损系数；P为两接触部件间的法向接触力；H为接触材料的硬度；L为两接触部件间相对移动的距离。

Archard磨损理论模型提出，摩擦副只有在接触表面较高的微凸体上才有相应的接触作用，上下微凸体接触后，因为相对运动和载荷的作用而产生应力集中，从而发生塑性变形。图8为Archard磨损理论模型。由图可知，假设两半球状微凸体有接触并发生相对运动，则有

式中：a为接触表面半径；A为接触表面面积；FN为法向接触力。在摩擦磨损过程中产生的一个磨损微粒体积为

图8 Archard磨损理论模型

单位时间内相对移动的距离为

则体积磨损率为

则在整个相互接触平面上有

其中单位时间内相对移动距离可以表示为

式中v1，v2分别为上下运动体（钢球和星形套）接触点的线速度。则体积磨损率可表示为

将前述中求得的转速差（v1-v2）和法向接触力QNQ代入上式，得

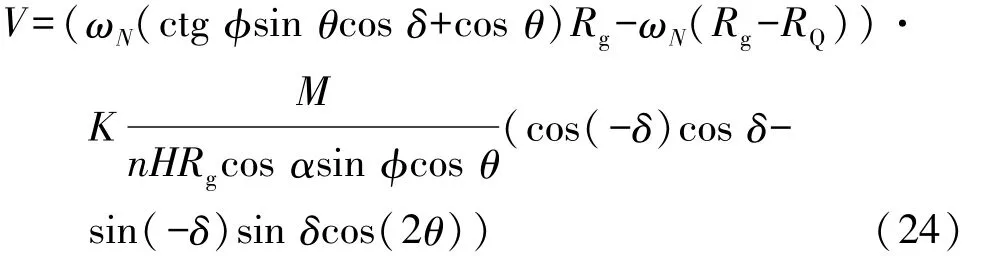
式中：n为钢球数；φ＝arccos（e cosθ/Rg）。

取K＝1.1977×10-4，H＝355 MPa，求得的体积磨损率V的单位是m3/s，与数学模型中等式右侧的计算单位相同；由上式可以看出，体积磨损率V是星形套端输入轴转速ωN、转角δ和轴间摆角2θ的函数。在球笼式等速万向节运动过程中，转角δ一直是个变量。图9和图10为七沟道和六沟道球笼式等速万向节钢球和星形套间体积磨损率V与转角δ、轴间摆角2θ的关系曲线。由图可知，在输入轴转速ωN不变的情况下，体积磨损率V随着转角δ在旋转一周的过程中呈周期性变化，在0°，360°转角位置时最大，此时钢球运动到沟道的最外端位置；在90°和270°转角位置时最小，此时钢球运动到沟道的中间位置。体积磨损率V随着轴间摆角2θ先变大再变小，最大单位时间内体积磨损率值约为 9.0×10-10mm3/s。

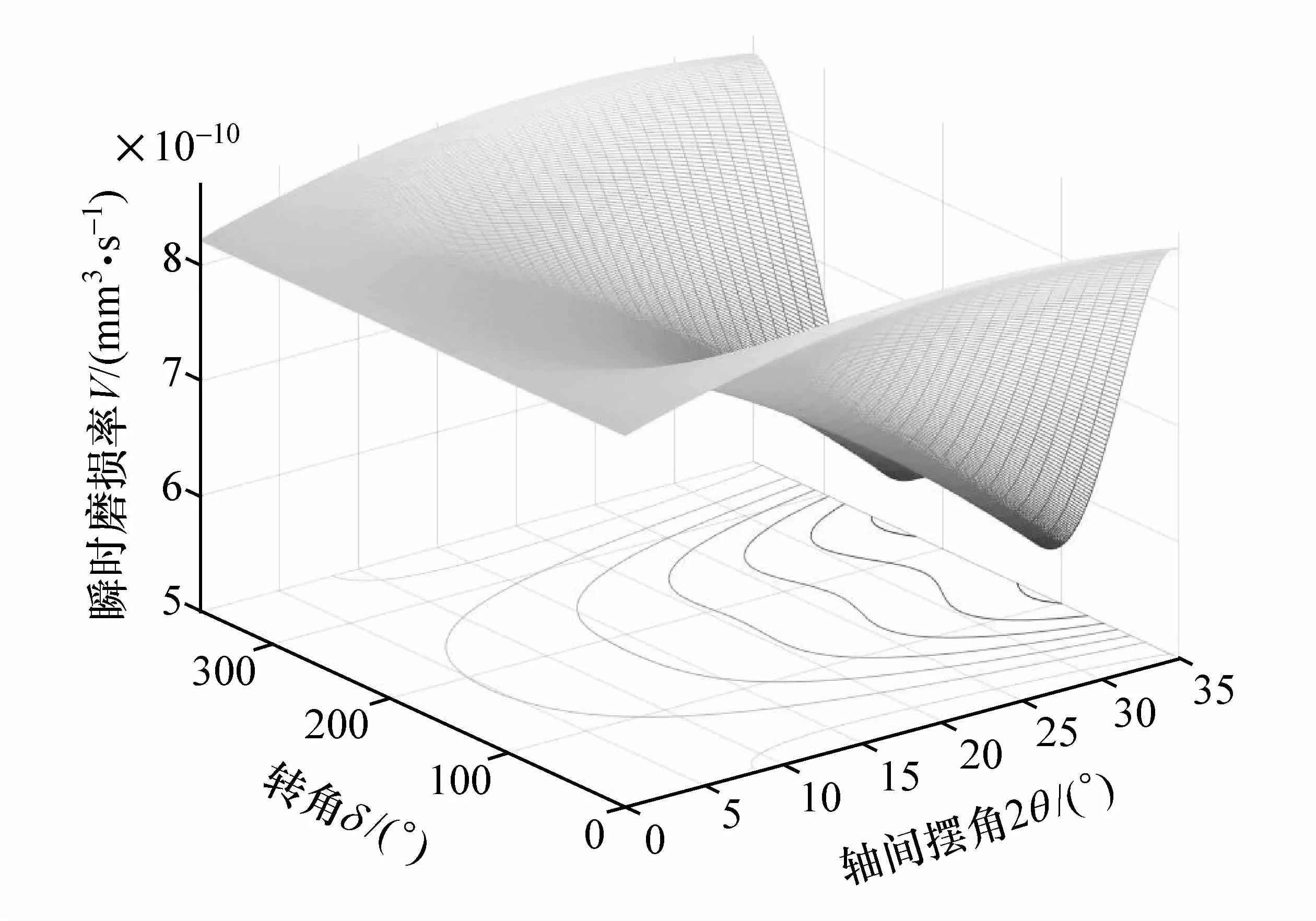
图9 七沟道的体积磨损率V特性

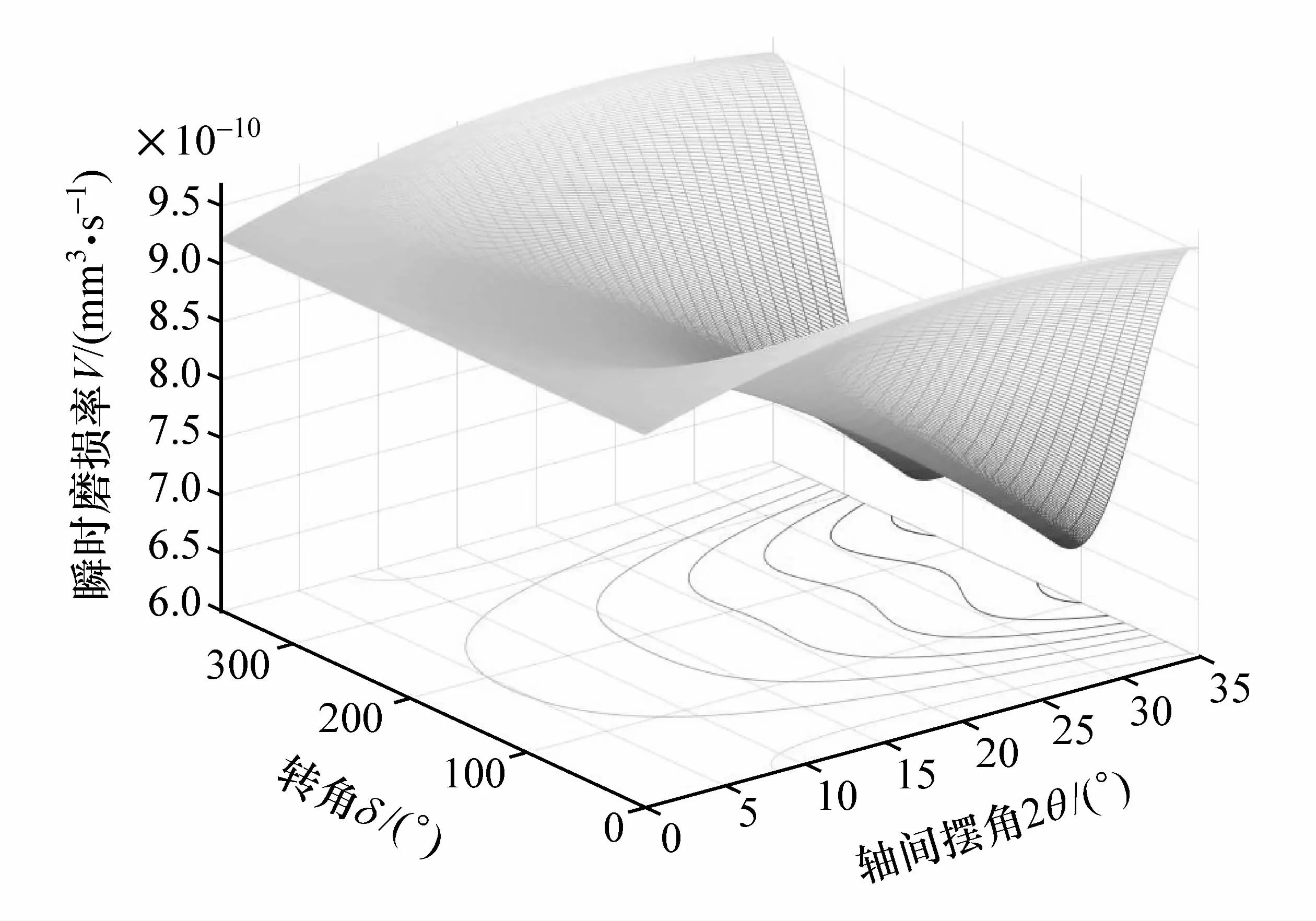
图10 六沟道的体积磨损率V特性

图11 为轴间摆角为35°时体积磨损率随着钢球与最外端的距离的变化规律。由图可知，体积磨损率V随着轴间摆角2θ先变大再变小，最大单位时间内体积磨损率值分别约为 9.0×10-10和 10.0×10-10mm3/s。

图11 瞬时磨损率V随钢球与最外端的距离的变化规律

由于磨损是一个持续的过程，单位时间内体积磨损率越小，能够获得更长的使用寿命，图12为体积磨损率V随转角δ和输入轴转速ωN的变化规律。由图可知，在轴间摆角2θ不变的情况下，单位时间内体积磨损率V随着转角δ在旋转一周的过程中呈周期性变化。在0°，360°转角位置时最大，此时钢球运动到沟道的最外端位置；在90°和270°转角位置时最小，此时钢球运动到沟道的中间位置。随着星形套端输入轴转速ωN的增长而线性增长，最大转速时的最大体积磨损率值分别约为9.0×10-10和10.0×10-10mm3/s，六沟道球笼式等速万向节的最大单位时间内体积磨损率要略大于革新的七沟道球笼式等速万向节。

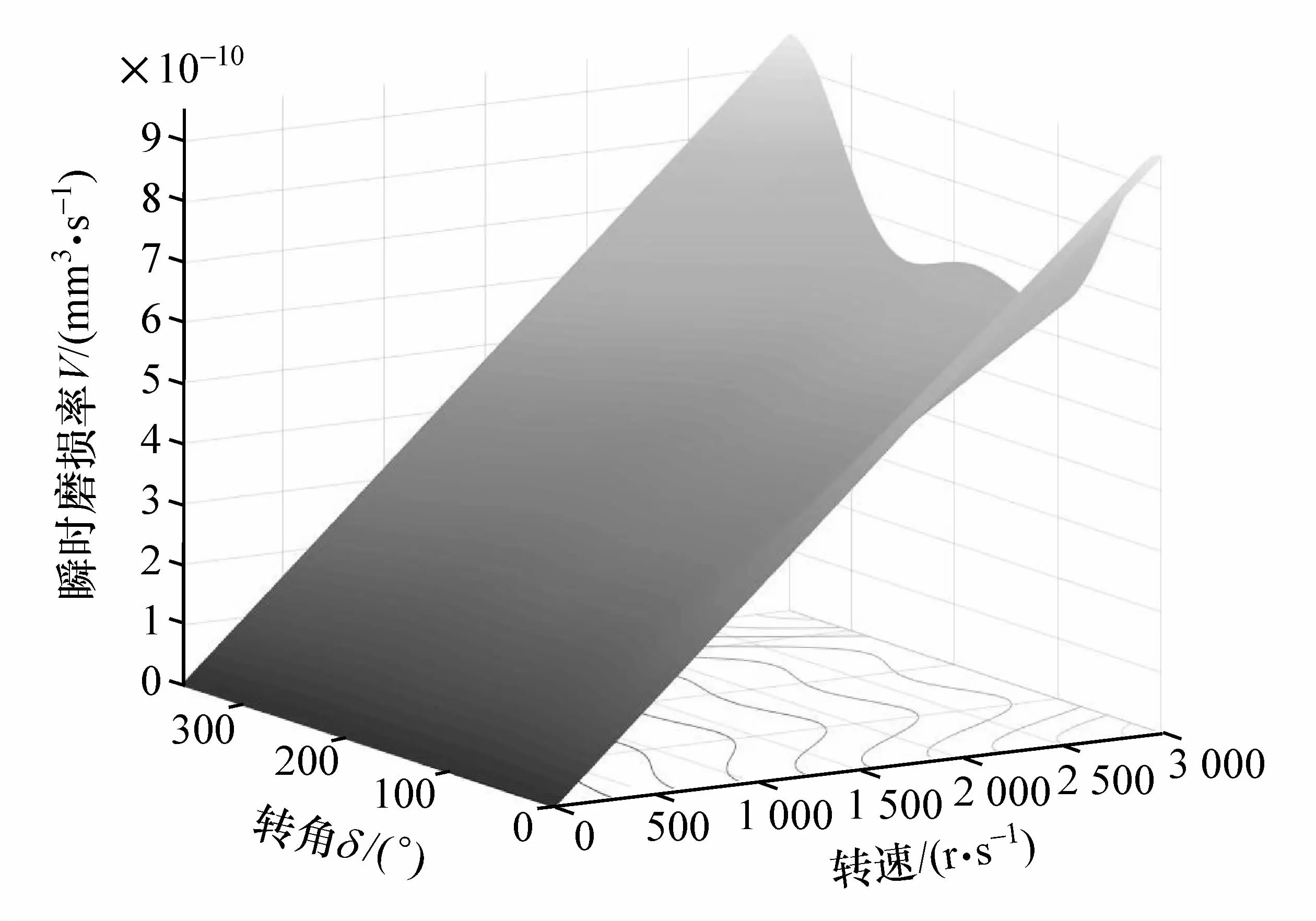
图12 体积磨损率V随转角δ和输入轴转速ωN的变化规律

6 仿真分析

本文中采用SolidWorks完成了七沟道球笼式等速万向节的几何模型构建以及装配。根据七沟道球笼式等速万向节结构参数，完成了几何模型的构建，利用几何模型完成后续的动力学建模及仿真过程。将球笼式等速万向节分别调整装配至轴间摆角为0°（零摆角工况）和 35°（最大摆角工况），将 360°/s2的角加速度和125 N·m的转矩施加在星形套与大地所构成的旋转副约束上，同时为保证受力平衡，需要在钟形壳输出轴端设置与输入端等大反向转矩，并按照仿真时间1 s、步长0.001进行仿真［9-10］。

（1）摩擦力测试

与星形套对钢球法向力的仿真值相同，图13和图14为七沟道球笼式等速万向节在轴间摆角为0°和35°情况下，钢球与星形套摩擦力随转角的变化情况。旋转一周过程中，星形套对钢球的法向力仿真值也需要借助Matlab的二次计算而得出。由图13和图14可知，仿真值与理论值的变化规律高度吻合，由于动静摩擦转换系数值的选取、接触变形导致的从点接触变为小椭圆面接触等因素导致仿真值略大于理论值，但误差不足10%，处在可以接受的允许误差范围内。

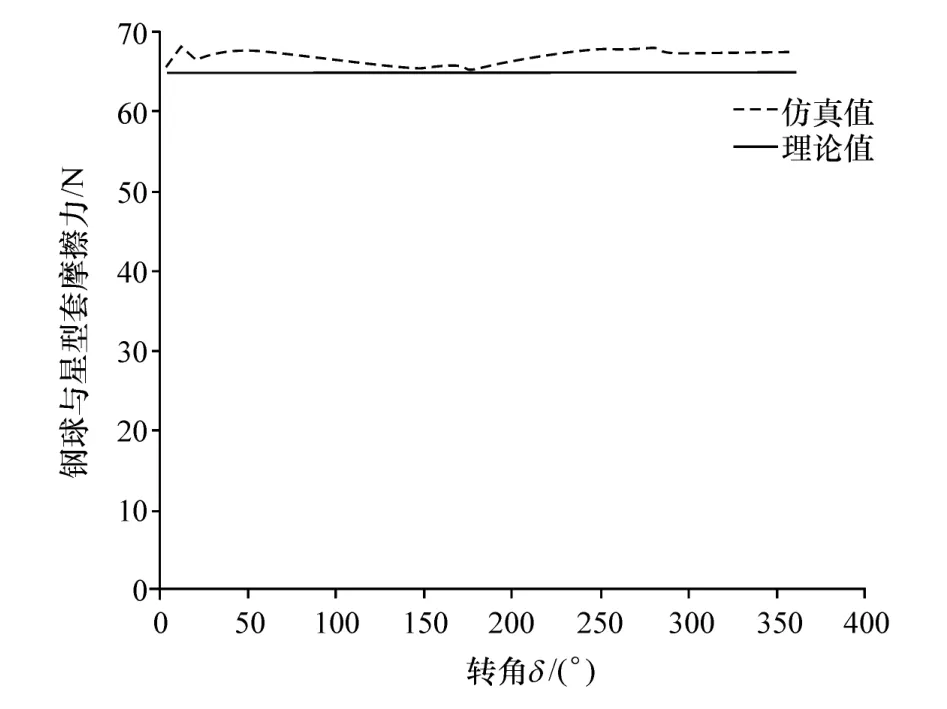
图13 轴间摆角为0°时摩擦力

（2）瞬时磨损率测试

与星形套对钢球法向力、摩擦力的仿真值相同，图15和图16为球笼式等速万向节在轴间摆角为0°和35°情况下，旋转一周过程中星形套与钢球间的瞬时磨损率随转角的变化情况。由图可知，仿真值与理论值的变化规律基本一致，数量级保持一致，两者微小偏差在可以接受的范围内。通过对轴间摆角为0°和35°时，七沟道球笼式等速万向节星形套对钢球的周向力、法向力、摩擦力和磨损率仿真值和理论值的仿真可以发现，球笼式等速万向节的运动学与动力学的仿真试验可信度较高，可作为今后研究疲劳等工作的基础和依据。

图14 轴间摆角为35°时摩擦力

图15 轴间摆角为0°时磨损率

图16 轴间摆角为35°时磨损率

7 结论

（1）钢球在沟道内既滑又滚的运动模式，摩擦力包含滑动摩擦力和滚动摩擦力，并且在钢球运动过程中随着钢球运动方向的改变，摩擦力的方向也会随之而变，摩擦力的正负会有所改变；

（2）钢球在沟道内受到的摩擦力是转角δ和轴间摆角2θ的函数，在转角δ一定时，摩擦力随着轴间摆角的增大而增大，摩擦力随着转角δ的变化呈周期性变化；

（3）保持架窗口对钢球的摩擦力随着轴间摆角的增大而增大，但该摩擦力本身的值和变化范围都非常小；

（4）球笼式等速万向节的磨损类型为疲劳磨损，体积磨损率V随着转角δ周期性变化，随轴间摆角的先变大再减小；

（5）七沟道等速万向节比六沟道内的摩擦力均小，同样的使用工况条件下，可以获得更长的使用寿命。