正反结合法在数学学习和教学中的应用

魏选平

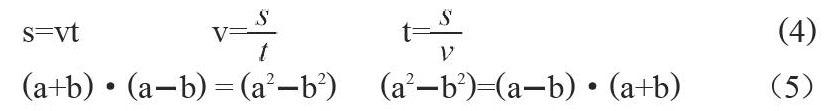
摘 要 本文详细介绍了正反结合的教学法在小学、中学及大学学习中的体现，反映出辩证的哲学思想，此方法对现实的数学教学具有很强的指导性。

关键词 正反结合 哲学 数学教学

中图分类号：G623.5文献标识码：A

0引言

矛盾无处不在，万事万物都有矛盾。一切事物的发展过程中，都有主要矛盾和次要矛盾，同一矛盾中又有矛盾的主要方面和次要方面。反映在生活中有正有反，有好有坏，有上有下，有左有右，有前有后。体现在数学上将贯穿于小，初，高，大的始终。数学是对客观世界从数量关系和空间位置两方面进行研究的学科，数学作为具体科学是哲学的体现，哲学又为数学的学习和研究提供了指导。无论数学计算和应用题，正反结合的原理都可以用来很好地指导解题过程。此外，该原理也在数学学习中发挥着巨大作用。

1正反结合法的应用

1.1正反运算是方程和等式移项的本质

小学四年级都学习了含有未知数的等式为方程。方程的移项原理是移项时，加变减，乘变除。那么，这样简单地推理出移项时一种运算变成它的反运算。

那么，这样的移项原理也来自于实际生活。物理上用天平秤物质质量时，左物右码，左边放物质后，右边如放1克和2克的砝码天平平衡时，体现左边物质质量为3克，可用1+2=3表示。如左边去掉1克重物，要使天平达到新的平衡，需去掉右边的1克砝码。这就相当对上边1加2等于3的等式两边同时减去1，就变成2=3-1，这也相当于1由等号左边移到右边变成减1了。初步说明移项原理为加变减。同样，4x2=8的等式两边同时除以2，就变成4=8？。这也相当于2由等式左边移到右边乘变除的道理。这都说明等式移项的原理是一种运算变成它的反运算。

初中的乘方与开方是一对反运算，在等式移项中也能体现。如式1所示，如2的立方等于8，将立方运算由左移到右边就变成了开立方，即2等于8的开立方。

23=8                     2=                                                     （1）

高中的指数与对数是一对反运算，在等式移项中也能体现。如式（2）所示，如2的立方等于8，当底数2由右边移到左边时，就由指数运算变成了对数运算，即形成3等于以2为底数的8的对数。

23=8                    3=log                                                     （2）

大学中的微积分也是正反结合的体现，如式（3）所示，x立方的导数等于x平方的3倍，将导数运算由等式的左边移到等式的右边，就得到x立方等于x平方的3倍的不定积分。

（x3）'=3x2               x3=3x2dx                                            （3）

1.2正反结合的应用

做数学题的过程是用学過的公式和定理进行等量变换下的化简过程。等量变换保持了所研究问题的性质，使所做的问题不会变为別的问题。化简是利用加减乘除移项合并化繁为简的过程，只有化繁为简才能解决问题，否则，止步不前，或化简为繁，越做越难，不可能解决问题。正因为推导的每一步都是等量变换，所以，正反结合可利用回推法来验证每一步推导是否正确。

一个公式，利用移项和等量变换原理可以由一个生发出多个公式。例如：如式（4）所示。路程等于速度乘以时间。移项后可以得到时间等于路程除以速度，也可得到速度等于路程除以时间。三个公式虽然形式不同，但本质一样，都从不同角度揭示了物体运动过程中路程，速度和时间的关系。如式（5）所示，初中的因式分解和多项式相乘也互为逆运算。其次，解二重积分时，当被积函数是二元函数时，对x和y进行积分，将二元函数转化为一元函数的过程是二元函数求偏导的逆运算。

s=vt                v=               t=                                      （4）

（a+b）·（ab） = （a2b2）      （a2b2）=（ab）·（a+b）            （5）

1.3正反结合的本质及意义

由上可见，方程或等式移项的原理，本质上是在方程或等式两边同时进行相同的运算得到的，所以其本质仍然是等量变换。数学是从数量和几何两方面对客观世界进行研究的学科。做数学题的过程是等量变换下的化简，中间等量变换的每一步形式不同但本质相同，每等量化简一步就向结论靠近一步，等量化到最简，既做对做完了题，又揭示了问题的本质。所以，做数学题的等量变换下的化简过程就是揭去层层伪装，透过外表看本质的过程。透过外表看本质是一种智惠，凡事只要能透过外表洞察到本质，就能一步到位，少走弯路。另外，做数学题的关键是读懂题，只有在读懂题的基础上，才能利用学过的公式定理搭建已知和未知的桥梁。从这个角度来说，读懂题也就是实事求是，恰当利用公式定理也就是按客观规律办事，所以，正确地做一道题的过程就是一切从实际出发，实事求是，按客观规律办事的过程。因此，每做对一道题就强化了一切从实际出发按客观规律办事的能力。只要坚持一切从实际出发，按客观规律办事就能无往而不胜。

等量变换意义重大，生活上讲得失相关，喜忧参半，利弊相关。物理化学上有质量能量守恒，哲学上有矛盾的辨证统一律。矛盾普遍存在，事物中的主要矛盾和矛盾的主要方面决定了事物的发展状态，主次矛盾和矛盾的主次方面的相互依存，相互排斥促成了事物的发展。万事万物都遵循自然辨证法，任何事物发展都是辨证的，只有把握好度，才能促成事物稳定长远地发展。这个度不可能绝对把握好，只能尽力而为地把握，要努力地向这个度去接近。

2结论

综上所述，正反结合法在方程和等式的移项化简中作用巨大，在代数式等量推导中每一步的检验中也发挥着作用，无不显示出正反结合的原理覆盖了数学的方方面面和角角落落。只有有正有反 ，正反结合才能更全面地去分析和解决数学问题。只有正反结合，才能为我们进行数学学习和教学提供指导。