串列六边形截面桥塔气动干扰效应研究

张志杰,李永乐,向活跃,房 忱

(西南交通大学土木工程学院,成都 610031)

在土木工程领域,越来越多地出现多个建筑或者建筑构件彼此相邻的情况,如相邻的两幅桥梁[1],悬索桥的两根大缆[2],城市中的互相靠近的高层建筑等。由于相互之间的气动干扰,这些建筑或者建筑构件的气动力和它们单独存在时有着明显的差异。所以,研究串列的建筑或者建筑构件的气动相互干扰非常必要。

早在20世纪70年代,Zdravkovich[3-4]就对圆柱的气动干扰问题有了一定的研究。日本学者Kimura[5]通过风洞实验，研究了新建桥梁对已有桥梁的气动干扰效应,结果表明双幅桥梁在不同间距和不同风向角下的气动干扰效应十分显著。Irwin等[6]通过风洞实验的节段模型和全桥模型，研究了在塔科马老桥附近新建一座桥梁时两幅桥梁的气动稳定性。Jin[7]等通过试验研究了串列双幅斜拉桥的涡激共振的气动干扰效应；刘志文等[8-10]对串列双幅断面的涡激共振稳定性、颤振稳定性、三分力系数气动干扰效应，进行了相关的风洞试验或数值模拟。林震云[11]从气动刚度和气动阻尼的角度，分析了双幅桥梁的气动干扰效应对下游桥梁的颤振稳定性的影响。刘多特等[12]采用一种改进的数值模拟方法,研究了主梁断面高度、来流风攻角及风向等因素对错列双钝体断面间的气动特性影响。李胜利等[13-14]通过CFD数值模拟,研究了串列钝体的三分力气动干扰效应和门形桥塔驰振气动干扰效应。陈星宇[15]以数值模拟的方法研究了悬索桥门形桥塔双柱串列的气动性能。路毓[16]对大跨桥梁的桥塔的吊索钝体群的气动干扰进行了数值分析。唐浩俊[17]以桥塔的两串列带圆角方柱为研究对象,研究了风速、风向角和间距比对截面气动力系数的影响。李燕玲等[18]与试验结果对比验证了DES方法在高雷诺数并列双圆柱绕流的准确性。已有研究大多通过风洞试验或数值模拟直接得到气动干扰效应的结果,分析过程较少而且分析的截面大都比较常规,多为矩形或者箱形。综合上述文献,针对特殊截面形式的串列建筑或者建筑构件的气动干扰问题有必要进行深入的研究。

本文根据一座人字形串列六边形截面桥塔的斜拉桥,分别取塔柱的上游、下游单个截面和不同间距的串列双柱进行CFD数值模拟,得到各种情况下的三分力系数,并结合压力云图进行气动干扰效应的分析,为桥梁抖振和驰振的研究提供依据。本研究的桥塔截面为沿桥梁横桥向不对称的六边形截面,气动力特性较为特殊,相关研究较少,研究其气动力特性非常具有工程意义。

1 分析模型

1.1 工程概况

某大桥的主塔为人字形桥塔,主塔正面如图1所示。桥塔截面在横桥向为不对称的六边形截面,为研究串列双柱的气动干扰效应,分别取上游、下游单个桥塔截面以及选取如图1所示3个高度位置处的塔柱进行数值模拟研究,3个高度位置处的串列塔柱从高到低分别为截面1、截面2和截面3。高度不同,串列塔柱截面的间距就不同,高度越低,间距越大。

图1 桥塔正面及桥塔截面(单位：m)

由于塔柱截面是渐变的、相似的,单个截面情况选取3种高度位置中顶部的截面进行研究。计算风攻角在-10°～10°,每2°为一个工况的三分力系数。图2给出了计算风攻角和风向。

图2 攻角和风向示意

1.2 计算域以及网格划分

利用Flunent 14.0计算流体力学软件,对单个桥塔塔柱截面进行数值模拟时,参考有关文献[19],为保证阻塞率小于3%的要求,上侧和下侧边界距离截面形心200 m,而上游边界距离截面左侧边界150 m,下游边界距离截面右侧边界450 m,模型缩尺比为1∶100。网格的划分兼顾计算精度和计算效率,在靠近截面区域采用非结构化网格,适当加密网格；在远离截面区域,适当让网格稀疏,采用结构化网格。计算域网格划分如图3所示,划分网格数量为20万个。计算域的边界条件设置为：上游侧设为速度入口,入口速度为15 m/s,下游侧设为压力出口,上下侧为对称边界条件,桥塔的六边形截面设为无滑移壁面。本文计算时所采用的湍流模型为SSTk-ω模型,时间步长取为t=0.001 s,待计算稳定后便可以计算三分力系数。对串列桥塔塔柱截面进行数值模拟时,计算域大小和模型缩尺比以及网格划分方法同单个截面,计算域网格划分如图4所示。边界条件和湍流模型与单个截面的相同,时间步长同样取为t=0.001 s,分别监视上游、下游截面的三分力时程结果,待计算稳定后计算三分力系数。

图3 单个截面计算域网格划分

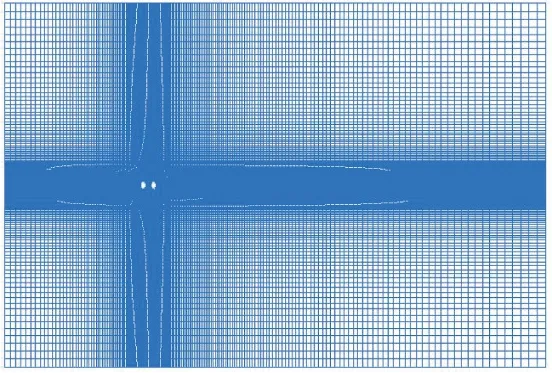
图4 串列桥塔截面计算域网格划分

2 数据处理及模型验证

在计算稳定后,根据数值模拟得到的三分力系数按照式(1)～式(3)计算截面的三分力系数平均值。

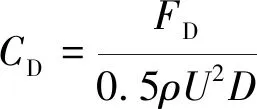
(1)

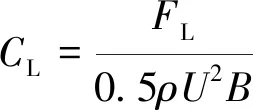
(2)

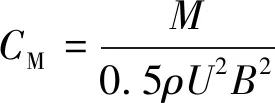
(3)

式中,ρ为空气密度；U为来流风速；D为垂直于来流方向的截面高度；B为平行于来流方向的截面宽度。

为了验证数值模拟的正确性,采用14 m×14 m的正方形截面,缩尺比为1∶100,网格划分、边界条件及Fluent中的设置同单个桥塔截面。图5为正方形截面的三分力系数数值模拟结果和文献[20]的对比图。从图5可以看出,正方形截面在攻角为0°时的阻力系数最大,正攻角时随攻角的增大而减小,负攻角时随攻角的增大而增大,正攻角和负攻角的模拟值呈对称关系；而升力系数随着攻角的增大而减小,斜率为负值。从模拟结果来看,阻力系数和升力系数与文献的试验值吻合程度较好,虽然部分攻角下略有偏差,可能是由于缩尺比不同,文献试验存在的误差等因素的影响,可以认为本文所采用的数值模拟方法是正确且合理的。

图5 正方形截面静风系数模拟值与文献试验值对比

3 塔柱气动特性分析

3.1 单个塔柱的气动特性

上游、下游桥塔截面的三分力系数模拟结果如图6所示。

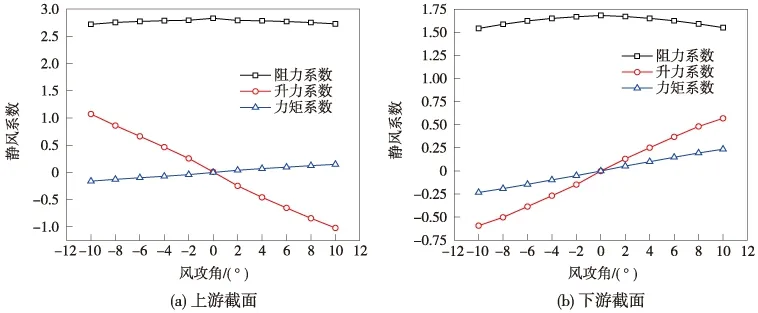
图6 单个桥塔截面三分力系数

比较两个截面的模拟结果,可以看出上游、下游桥塔截面的阻力系数在0°攻角时最大,正攻角时随攻角的增大而减小,负攻角时随攻角的增大而增大,正攻角和负攻角的模拟值呈对称关系；上游截面比下游截面的阻力系数大,从图7的压力云图来看,这可能是由于下游截面在来流风作用下更呈流线型,对来流的阻挡作用更小；上游截面的升力系数随风攻角的增大而减小,下游截面的升力系数随风攻角的增大而增大,可能是由于上下游两个截面在横桥向是不对称的且差异较大,所以上下游两个截面的变化趋势完全相反；而上下游两个截面的力矩系数随攻角的变化趋势一致,且下游截面的力矩系数较大。

图7 单个截面0°攻角的压力云图

3.2 串列桥塔的相互气动干扰

在计算结果稳定后,提取出三分力监视结果,按照第2节公式计算得到三分力系数平均值。为了能够直观地分析串列截面的气动干扰效应,将单个截面的三分力系数和串列截面的三分力系数绘于一张图上。图8是不同间距串列塔柱的上游截面与单个上游截面的三分力系数图。图8(a)表明,截面1串列两截面距离很近,从图9的压力云图可以看出,上游截面的阻力,相互之间的气动干扰效应导致上游截面的阻力系数与单个截面相比有所增加,而且在0°风攻角附近,这种阻力系数的增加效应最大；截面2和截面3两截面之间的距离增大,由于塔柱间干扰效应会减弱,截面2和截面3的上游截面的阻力系数会比单个截面的有所减小。图8(b)的结果说明在0°风攻角时，各截面的升力系数与单个截面的相同,但是当攻角较大时,各工况在气动干扰效应下有不同程度的差异。从图8(c)中,可以清楚地看出截面1在攻角较大时,串列塔柱的气动干扰效应会使得力矩系数与单个截面的差异较大,且随着两截面间距离的增大,这种差异会减小。

图8 不同间距上游桥塔截面与单个上游截面三分力系数

图9 0°攻角下不同间距串列塔柱的压力云图

图10为不同间距串列塔柱的下游截面与单个下游截面的三分力系数图。图10(a)表明,各截面的下游截面的阻力系数都比单个截面的小,从图9的压力云图可以看出,这是由于上游截面的遮挡效应造成下游截面的阻力明显降低；而截面1两截面的距离最近,气动干扰效应和上游截面的遮挡效应最大,下游截面出现负压,阻力系数最小为负值；截面2和截面3两截面的距离比截面1的距离大,遮挡效应和气动干扰效应减弱,下游截面压力增大,阻力系数增大。从图10(b)可以看出,由于上游截面的遮挡效应,各截面的下游截面升力系数的斜率比单个截面的要小。图10(c)的结果表明,3种截面下游截面的力矩系数基本相同,与单个下游截面相比,随着攻角的变化,整体变化趋势相同,但力矩系数增加较小。

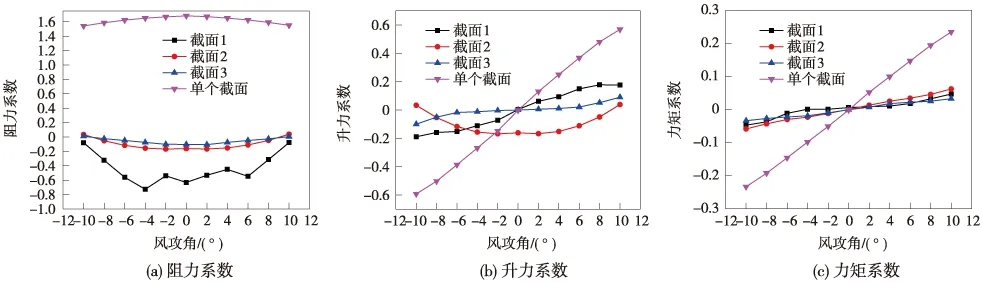
图10 不同间距下游桥塔截面与单个下游截面三分力系数

4 结论

通过数值模拟,分析了串列桥塔的相互气动干扰,考察了风攻角、塔柱间距等因素的影响,得出如下结论。

(1)对单个塔柱截面来说,上游截面比下游截面的阻力系数大,随攻角变化的规律相同；上下游截面的升力系数的变化趋势相反；上下游两个截面的力矩系数基本相同。

(2)对串列塔柱的上游截面来说,距离较小时,阻力系数比单个截面的要大,距离较大时,阻力系数比单个截面的要小；塔柱间距离变化时,升力系数和力矩系数的差异较小。

(3)对串列塔柱的下游截面来说,下游截面的阻力系数都比单个截面的小,塔柱间的距离增大时,阻力系数有所增大；而升力系数和力矩系数的斜率都比单个截面的要小。