高速铁路道岔三维表面模型生成方法研究

董飞飞,岑敏仪,2,3,江来伟,申彦军

(1.西南交通大学地球科学与环境工程学院,成都 610031； 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031； 3.西南交通大学高速铁路运营安全空间信息技术国家地方联合工程实验室,成都 610031)

高速铁路运营期间高速道岔各部位的尺寸和几何形位极易发生变化，因此道岔病害整治是铁路工务部门日常维护的重要工作[1]，目前道岔检测技术主要是定期采用轨道几何状态测量仪、道尺、支距尺、塞尺、检查锤、弦线等传统测量工具进行数据采集并和标准数据进行对比[2]，因而受外界因素影响大且作业效率低下，已难以满足铁路发展的需求。为提高数据采集效率和精度，近年来有学者[3-6]尝试采用非接触式测量进行道岔病害整治，即通过数字化技术或者机器视觉技术进行非接触测量得到道岔测量数据，通过与标准道岔对比，进而将道岔病害及状态直观呈现在工作人员面前。其中标准道岔模型的精度及可靠性将直接影响道岔病害诊断及整治效果，所以通过道岔检测数据判断病害位置及制定整治措施的基础便是道岔的高精度三维建模，寻找精确生成道岔数字表面模型的方法是建模的前提。

为生成道岔数字表面模型，吴淑定[3]利用三维扫描设备获得道岔表面点云数据，然后借助逆向处理软件CATIA逆向还原实体道岔CAD模型；Ilia Mokhtarian，全顺喜等[7-11]以变截面控制断面为依据，通过拟合插值法生成道岔轨道表面模型，其原理为：首先将心轨和尖轨已知CAD关键截面离散为离散坐标点，然后采用B样条曲线拟合典型断面离散点坐标，将离散点坐标表示为标准化弧长参数，最后通过线性内插得到尖轨和心轨区域任意位置处点云截面模型；吴安伟，李刚，曹保[12-14]则利用动力学仿真分析软件生成道岔轨道模型，但其本质上仍是通过拟合插值的方式获得；韩峰，康峰[15-16]基于建筑信息模型(Building Information Modeling，BIM)思想，对AutoCAD进行二次开发，实现不同号码道岔模型配置；胡明玥[17]通过求道岔上关键点坐标值，然后利用OpengFlight API编程实现道岔建模。上述学者虽然通过不同方法建立了道岔数字表面模型，但所得模型多是用于动力学分析或铁路三维设计，其精度无法满足高速铁路道岔检测要求。以高速铁路18号道岔中的核心部件曲尖轨和长心轨为研究对象，根据道岔设计图中尖轨和心轨沿里程方向变截面特性，研究其不同位置处钢轨轮廓的几何关系，提出以道岔几何设计参数生成区域变截面钢轨轮廓模型的几何方法。

1 高速道岔截面模型

1.1 模型特征

高速道岔由转辙器、导曲线以及辙叉组成，为保证列车过岔时岔区轨道平顺性，尖轨和心轨须刨切成变截面钢轨。转辙器区尖轨相对基本轨、辙叉区心轨相对翼轨有一定降低值，降低值沿着前进方向逐渐减小，且轨顶宽度逐渐加宽，最后分别和基本轨、翼轨齐平(图1)，曲尖轨和长心轨不同位置截面图见图2，曲尖轨和长心轨不同位置处轨顶降低值p及轨头宽度w见表1。

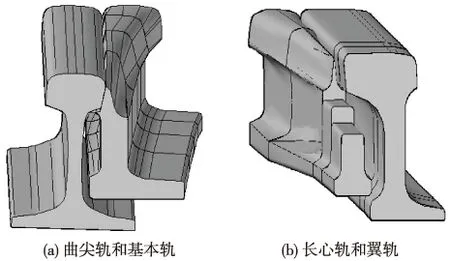
图1 曲尖轨、长心轨三维模型

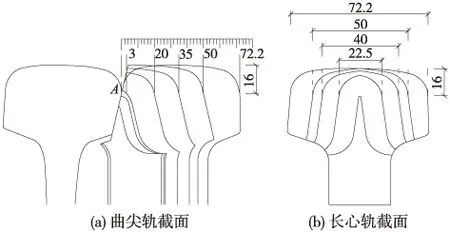
图2 曲尖轨、长心轨不同位置截面(单位：mm)

1.2 曲尖轨变截面轮廓模型

文献[18]表明，我国高速铁路道岔70%以上为国产客专道岔，其尖轨由国产60D40特种断面钢轨刨切而成，刨切轮廓轨头部位由不同半径圆弧以及与其相切的线段组成，如图3所示。确定曲尖轨变截面任意位置处轮廓模型，其本质是根据任意位置处已知截面几何参数，计算组成截面各段圆弧和线段节点坐标，即可得到任意位置处截面模型。

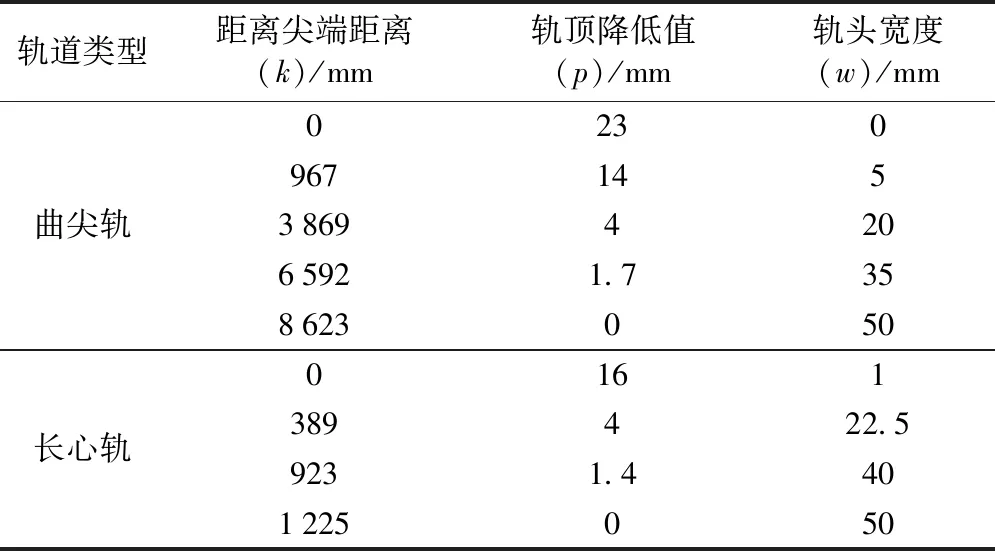
表1 曲尖轨和长心轨不同位置轨顶降低值及轨顶宽

注：轨顶降低值p为刨切截面顶端距离标准未刨切钢轨顶面的距离，轨头宽度w为标准钢轨顶面向下16 mm对应宽度。

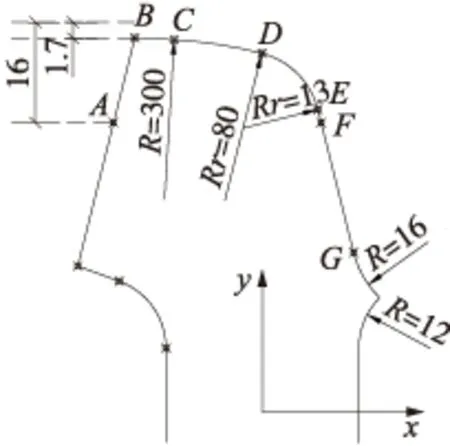
图3 曲尖轨35 mm轨顶宽轮廓(单位：mm)

根据曲尖轨设计文件，通过任意距离曲尖轨尖端距离k可知对应截面几何参数

Par(k)={pk，wk，xAk}

式中，pk为距离曲尖轨尖端k处轨顶面降低值；wk为轨头宽度；xAk为A点在以截面底边中点为原点，向右为x轴，垂直x轴向上为y轴的截面坐标系下横坐标值。

1.2.1 轮廓节点列坐标

(1)

式中，kAB、kEG和bAB、bEG分别为直线AB、EG斜率和截距。

由于曲尖轨由60D40钢轨刨切而成，其标准高度为142 mm，则yA=(142-16) mm=126 mm，yB=142-pk，且图3中直线AB、EG为1∶4固定刨切，故kAB和kEG为固定值，根据(xA，yA)以及yB可得到B点坐标(xB，yB)。

利用图3中不同半径圆弧和直线相切关系，节点列P满足以下关系

(2)

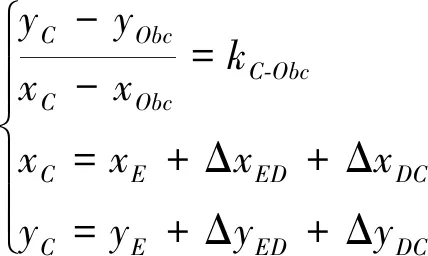
(3)

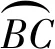
根据式(1)～式(3)可得节点列P的坐标，再结合各段圆弧对应半径，可得各段圆弧对应圆心坐标O(xi，yi)，i={Rr13，Rr80，R300}，据此可计算得到轨头每段圆弧对应弧长以及相切线段对应长度li。

1.2.2 轨头圆弧组成结构

由于曲尖轨具有变截面属性

虽然国产客专道岔曲尖轨轨头由半径为300，80，13 mm圆弧以及与其相切的线段组成，但随着轨头宽度w和轨顶面降低值p的变化，曲尖轨不同位置处3种半径圆弧并不会始终存在，只有当轨顶宽度达到一定界值后，轨顶右边半径为Rr80、R300圆弧和轨顶左边半径为Rl80、Rl13圆弧才会存在，因此只有确定轨顶面不同半径圆弧组成时对应轨头宽w界值后，才能根据给定k所对应w值确定截面轨顶圆弧组成结构，从而计算截面节点列坐标，最终得到曲尖轨任意位置处截面轮廓模型。

采用迭代法确定曲尖轨顶面不同半径圆弧组成对应w界值，具体流程为：

(1)给定初始曲尖轨尖端距离k，判断对应半径圆弧是否达到最大值的误差限ε以及k值增加的步长bk；

(2)根据给定k值得到截面几何参数Par(k)={pk，wk，xAk}；

(3)根据式(1)～式(3)计算节点列P坐标及对应半径为Ri(i=Rl13，Rl80，R300，Rr80，Rr13)的圆弧长度lk；

(4)判断lk是否达到半径为Ri的圆弧的最大值lmaxRi，如果没达到最大值，即|lk-lmaxRi|>ε，则k=k+bk，返回步骤(2)，否则lk达到对应半径为Ri弧长最大值，i=i+1，返回步骤(2)。

通过迭代计算最终得到曲尖轨轨头圆弧组成结构及对应w界值，如表2所示。

表2 曲尖轨轨头宽和圆弧组成对应表

1.2.3 几何法生成变截面钢轨模型

采用几何法计算曲尖轨任意位置截面轮廓模型的步骤为：

(1)迭代法确定变截面钢轨顶面不同半径(Ri)圆弧组成结构对应wi界值；

(2)根据给定距离曲尖轨尖端距离k，得到对应曲尖轨轨顶面几何参数Par(k)；

(3)根据式(1)～式(3)计算曲尖轨截面轮廓节点列坐标P及线型属性(O，l，R)；

(4)根据节点列P及线型属性信息，编写程序自动生成给定密度截面轮廓点云模型。

2 实验分析

为验证上述几何法生成道岔变截面钢轨轮廓模型的有效性，以高速铁路18号道岔曲尖轨、长心轨为例，根据已知截面几何参数，利用几何法和现有生成道岔截面数字模型的方法拟合插值法[8，19-20]，利用关键截面放样重建方法，分别生成曲尖轨和长心轨典型截面轮廓点云模型，然后计算3种方法所得曲尖轨和长心轨不同位置处截面轮廓模型同CAD设计模型偏差，偏差计算原理为：首先将CAD设计模型分离为间距为0.02 mm的离散点，所得坐标作为变截面设计模型真值，然后计算3种方法生成的变截面轮廓上不同截面轮廓点坐标同对应设计模型轮廓点的最小距离。为从局部和整体效果分别评价两种方法所得模型的优劣性，分别统计模型的最大偏差和偏差标准差，偏差统计结果见表3和表4。

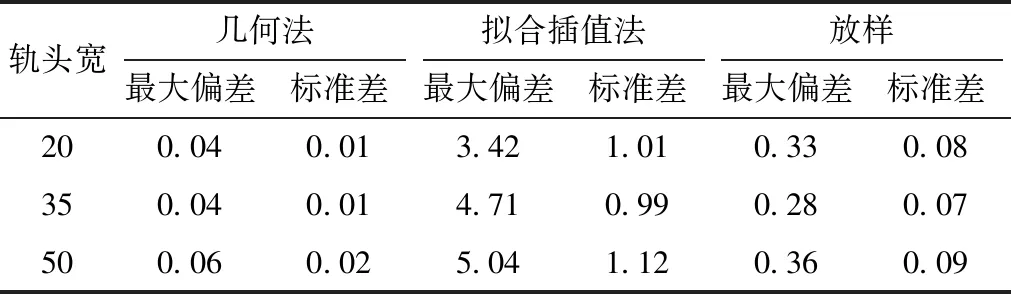
表3 曲尖轨不同方法生成模型同设计模型对比 mm

表4 长心轨不同方法生成模型同设计模型对比 mm

从表3、表4几何法和拟合插值法所得模型同设计模型的最大偏差可以看出，对于曲尖轨和长心轨不同轨顶宽典型截面，几何法相比于拟合插值法，其所得曲尖轨和长心轨典型截面轮廓模型和对应CAD设计模型最大偏差不超过0.1 mm，而拟合插值法所得模型最大偏差可达到5 mm。通过两种模型和设计模型偏差的标准差来看，几何法所得模型和设计模型偏差的标准差小于0.02 mm，拟合插值法所得模型和设计模型偏差的标准差可达到1 mm，说明几何法所得模型在和设计模型整体接近程度上明显优于拟合插值法所得模型。由于拟合插值法是利用给定特殊位置处截面点云通过拟合内插方式生成，故生成任意位置变截面模型精度会受到原始拟合截面个数和精度的影响，参与拟合内插的原始截面个数越少，生成的截面点云模型精度越低，而几何法则根据道岔各个截面属性值利用构成截面的圆弧与线段的几何关系生成，具有严密的数学模型，因此和CAD设计模型基本不存在偏差，精度高且能很好地反映出截面轮廓特征。

同时，利用关键截面对曲尖轨和长心轨变截面模型进行放样，所得模型和设计模型最大偏差为0.39 mm，偏差标准差小于0.1，所以通过放样所得模型精度比拟合插值法所得模型精度高，整体平滑性也优于拟合插值法，但不如几何法所得模型精确。由于通过关键截面放样变截面模型时需要事先设定放样路径，路径的数量和准确程度很大程度上影响了放样精度。

图4为几何法、拟合插值法和放样方法生成曲尖轨轨顶面宽20 mm和长心轨轨顶面宽40 mm截面模型以及对应CAD设计模型。从图4可以看出，几何法所得模型和设计模型可以很好地吻合，放样所得模型吻合程度次之，而拟合插值法的模型受到原始截面个数和精度的影响，所得模型和设计模型轮廓吻合程度最差，特别是轨顶截面变化区域存在更大偏差。

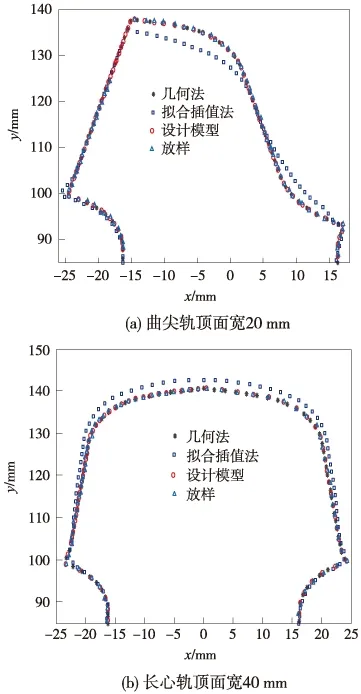
图4 不同方法生成曲尖轨和长心轨轨头模型对比

通过上述分析，几何法所得模型在局部最大偏差以及和设计模型整体接近程度上，均优于拟合插值法和放样方法所得模型。

3 几何法生成曲尖轨和长心轨模型

利用几何法生成高速铁路18号道岔曲尖轨和长心轨表面数字模型效果如图5所示。

图5 18号高速道岔曲尖轨、长心轨表面数字模型

4 结论

本文根据高速道岔尖轨、心轨变截面轮廓特征，利用几何法计算任意位置处轮廓的节点列及线型属性信息，实现高速道岔尖轨、心轨等关键位置处高精度数字模型生成。主要结论如下。

(1)提出生成尖轨、心轨等道岔关键区域变截面钢轨数字模型的几何法方法，并实现自动化生成。

(2)几何法生成高速道岔模型与现有的拟合插值法和放样重建方法对比。结果表明：几何法生成变截面钢轨轮廓模型与设计参轮廓模型标准差小于0.02 mm，模型的整体平滑性优于拟合插值法和放样重建方法。

(3)几何法生成道岔关键部位轨道表面模型与设计模型最大偏差不超过0.1 mm，可作为基础模型满足高速道岔病害探测和整治以及科学研究的需要。

(4)通过几何法生成道岔三维表面模型可作为子模型嵌入到铁路工程规划、设计、施工和运维全过程BIM模型中。