基于优化型滑模观测器的PMSM换相控制研究
寻志伟,王鑫明,刘向辰,杨沛豪,王小辉,寇水潮
(1.陕西国华锦界能源有限责任公司,榆林 719319;2.国网河北省电力有限公司,石家庄 730000;3.航空工业兰州万里航空机电有限责任公司,兰州 730000;4.西安热工研究院有限公司,西安 710054)
0 引 言
永磁同步电机(以下简称PMSM)作为目前工业领域广泛采用的一种电机,具有结构清晰明了、速度调节响应迅速、带负载能力强等优点[1-2]。为检测到连续的PMSM转子位置信息,实现电机的换相控制,PMSM大多利用霍尔位置传感器或光电码盘位置检测装置进行检测。这些位置传感器或位置检测装置不仅增大了电机的体积,增加了生产成本,且由于非一体铸造,在运行过程中常有各式各样的问题。因此,不安装此类传感器,用一些算法达到控制电机的目的,成为最近PMSM领域研究的热点[3-4]。
文献[3]提出确定反电动势波形过零点来间接得到转子位置信息方法,具体是通过电压采样电路得到任意导通两相的线电压,通过计算得到未导通相反电动势过零点进而得到装置位置,完成电机换相运行。文献[4]提出通过比较PMSM未导通相端电压和逆变器输入电压,计算得到该相反电动势,进而得到过零点即换相点。该方法在保证响应速度的同时,控制算法得到简化,提高了整个控制的性能。
间接得到转子位置信息完成电机换相,因观测器构造简单、鲁棒性能好、应用范围广,近年来获得业内广泛关注。状态观测器主要有龙伯格观测器[5]、卡尔曼观测器[6]、滑模观测器[7-10]等。滑模观测器较其他观测器具有模型建立简单、参数变化对观测器扰动小等优点。滑模观测器数学模型中利用符号函数代替偏差的实际值,具有较高的增益特性,加快了滑模观测器响应速度。文献[7-10]分别采用各种方案对滑模观测器进行改进,有效消除了抖振现象。
本文运用滑模观测器在线估计PMSM的反电动势,针对滑模观测器存在的抖振现象,应用双边层分段函数理论,将传统符号函数用新型切换函数代替,有效减小滑模观测器的抖振。最后通过仿真和实验验证了本方法的有效性。
1 PMSM数学模型
图1为PMSM系统的等效电路图。
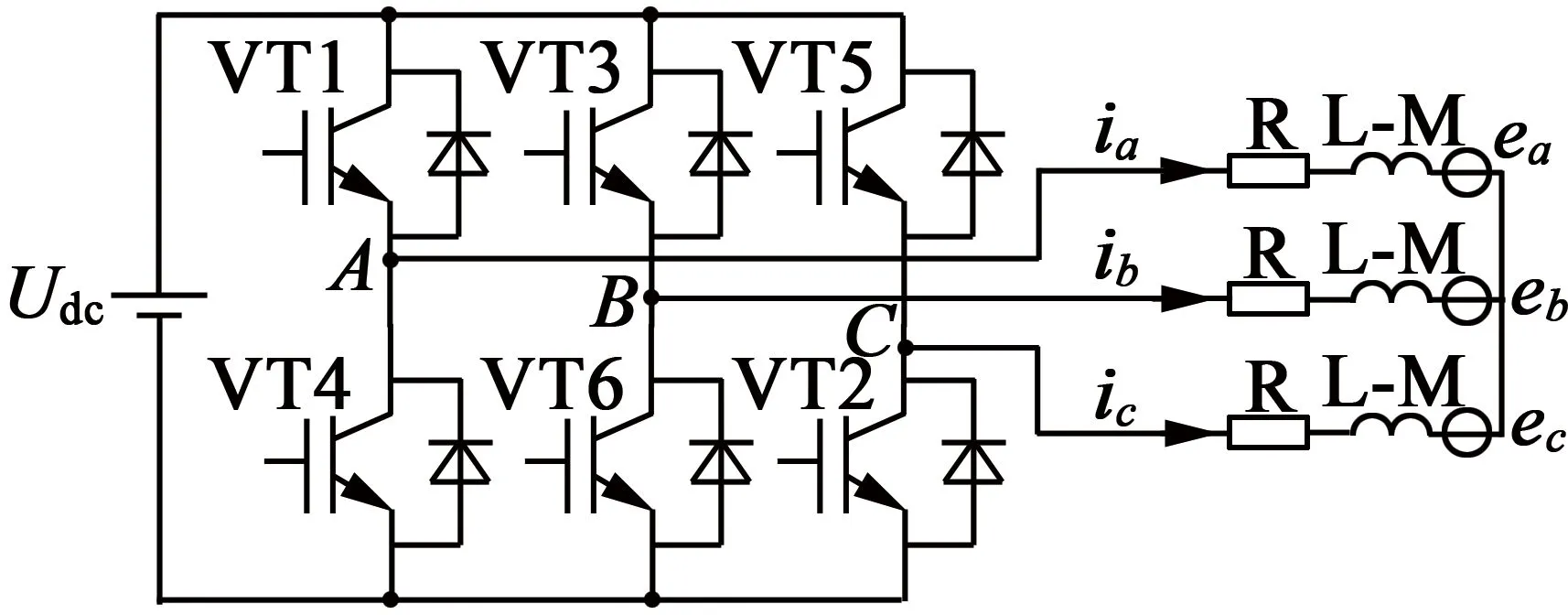
图1 永磁同步电机系统的等效电路图
假设其三相绕组对称,不计电机的涡流损耗和电磁滞损耗,为了减小计算量,将a,b,c三相采用Clarke变换转换到α,β静止坐标系下,则PMSM数学模型可以表示:
(1)
式中:
(2)
式中:iα,iβ为PMSM定子电流;Uα,Uβ为PMSM定子电压;eα,eβ为PMSM反电动势;L为定子电阻;L为定子电感;ψf为永磁体磁链;ω为转子角速度;θ为转子角度。
2 优化型滑模观测器的设计
2.1 优化滑模观测器设计
根据式(1)中PMSM状态方程,构建PMSM的滑模观测器:
(3)
式中:“^”为观测值;k1和k2为滑模增益;F(·)为切换函数。
传统滑模观测器切换函数F(·)一般采用符号函数sgn(·),其函数表达式:
(4)
滑模观测器的抖振现象是由于符号函数的不连续性导致观测器内存有大量的高次谐波引起的,为了有效减弱滑模观测器的抖振问题,通常采用无源LC滤波装置,但这会引起观测器输出值即观测值出现相位滞后问题,还需引入相位补偿装置。
本文研究一种利用双曲正切函数的新型切换函数。该新型切换函数可分为滑模切换平面内及滑模切换平面外两部分,滑模切换平面边界层用|δ|表示。该新型切换函数表达式:
(5)
双曲正切函数具有光滑连续特征,能够有效减小滑模观测器的抖振现象。滑模切换平面外,通过改变双曲正切函数的斜率来使系统控制更加灵活,使观测值可以快速、稳定到达滑模切换平面。从PMSM起动到以额定转速运行过程中,不同转速对应不同斜率a,缩短观测器响应时间。新型切换函数曲线如图2所示。

图2 新型切换函数图形
优化型滑模观测器误差方程可表示:
(6)

(7)
(8)
图3为优化型滑模观测器在PMSM中应用原理图。

图3 优化型滑模观测器原理图
2.2 优化型滑模观测器滑模增益确定
(9)

(10)



(11)

(12)
根据F(x)函数性质,F(x)与x符号一致且|F(x)|≤1,则可以推出:
(13)
3 仿真分析
根据上述方法,设计基于优化型滑模观测器的无位置传感器PMSM控制系统,其框图如图4所示。

图4 无位置传感器PMSM控制系统框图
在控制系统框图中,以转速控制为外环,转矩控制为内环。
为了验证基于优化型滑模观测器的PMSM无位置传感器控制系统性能,分别建立基于MATLAB仿真软件的传统滑模观测器和优化型滑模观测器仿真模型,对两种不同观测器的输出即反电动势进行比较。通过负载突变,验证本控制系统的抗干扰能力。PMSM参数如表1所示。

表1 PMSM参数
当电机以转速n=300r/min,负载转矩TL=3 N·m运行时,图5给出了传统滑模观测器输出的反电动势观测值与实际值对比,优化型滑模观测器输出的反电动势观测值与实际值对比。

(a) 传统滑模观测器

(b) 优化型滑模观测器
图5中,优化型滑模观测器输出值与传统滑模观测器输出值相比,波形更为平滑,有效消除了抖振现象。
图6(a),图6(b)分别对传统滑模观测器和优化型滑模观测器输出值与实际值之间的误差进行对比。

(a) 传统滑模观测器
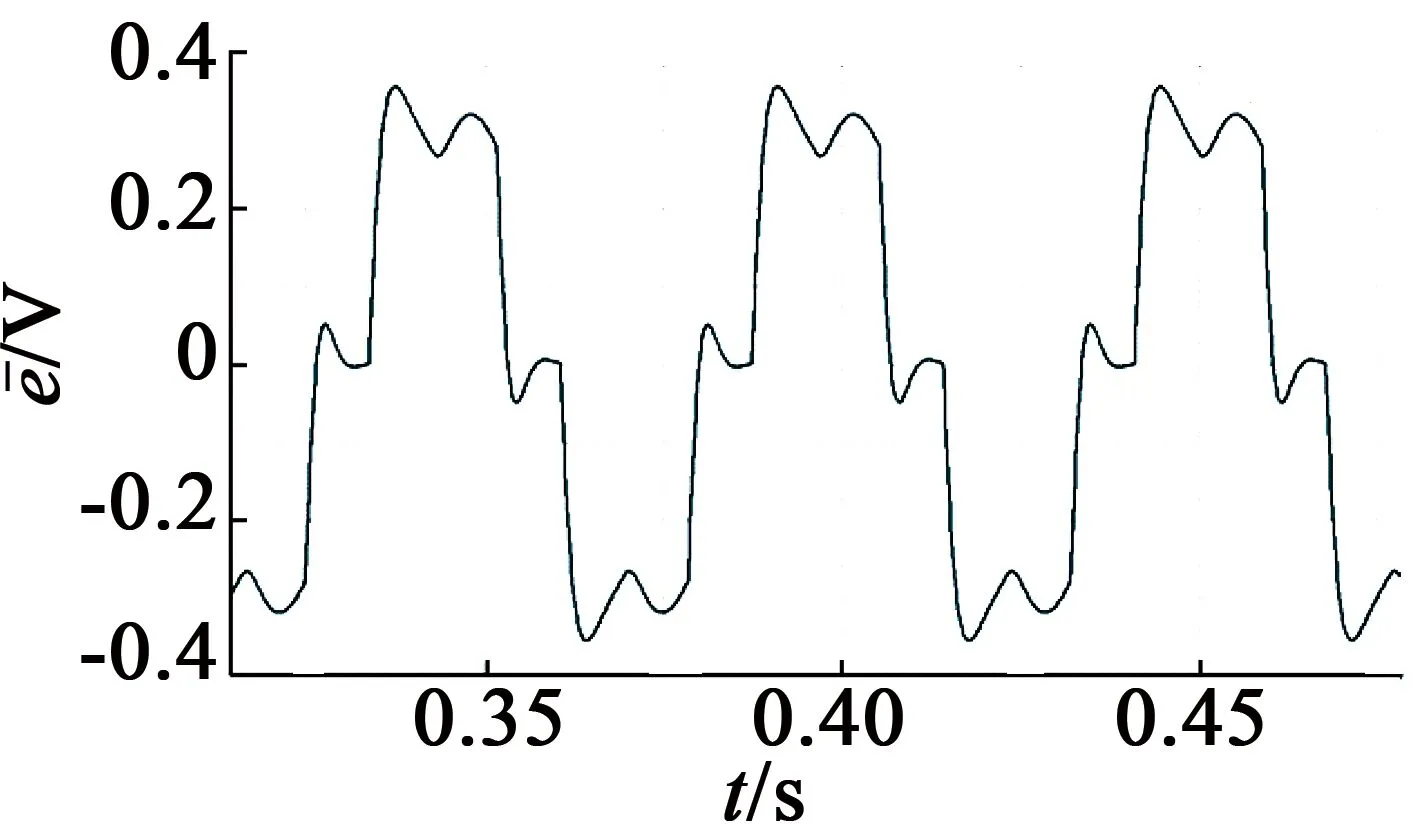
(b) 优化型滑模观测器
根据对比图可以得知,优化型滑模观测器输出值与反电动势实际值之间误差可以降低至2%,更加接近实际反电动势,且有效消除了抖振现象。
图7给出了本文设计的滑模观测器计算得出的PMSM转子位置信息与实际PMSM转子位置对比图,观测值与实际值几乎重合。
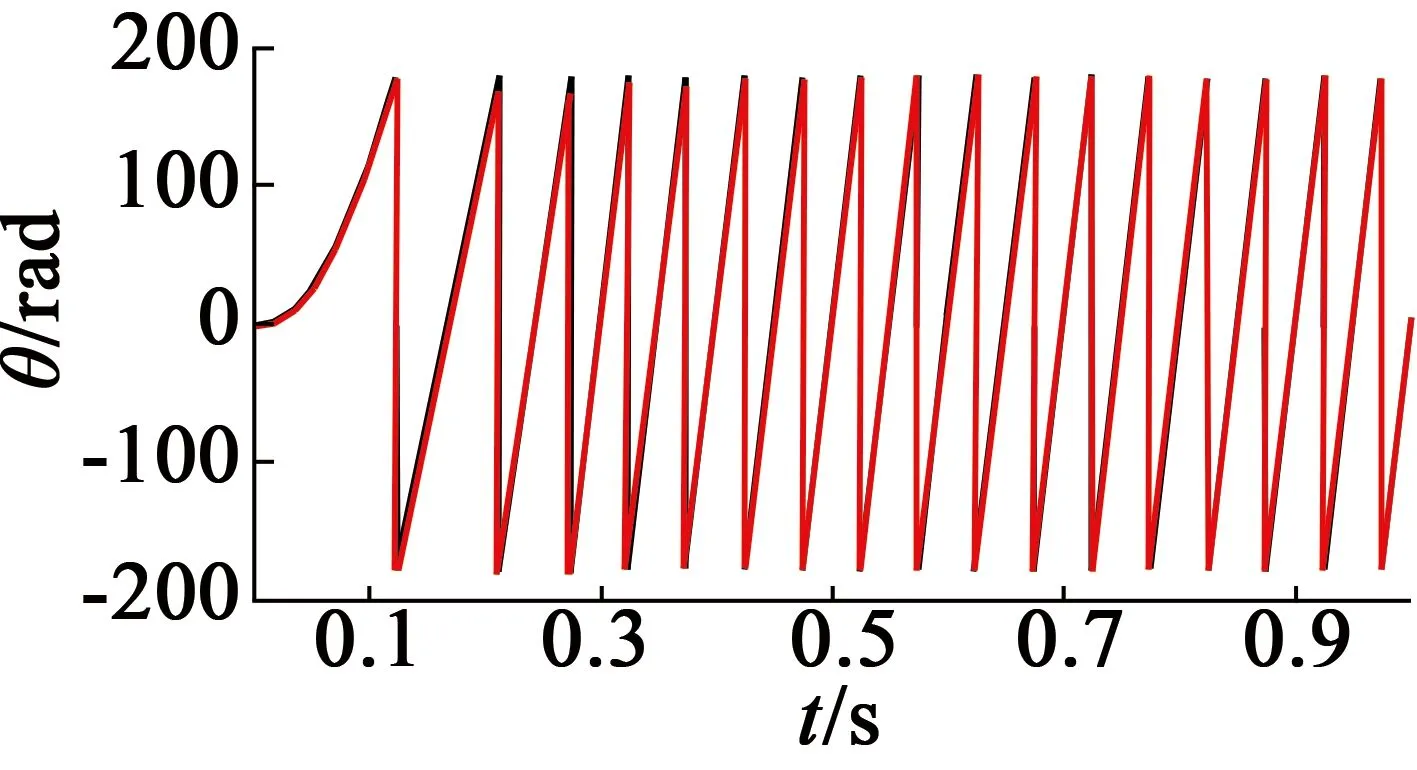
图7 优化型滑模观测器中转子位置观测值与实际值
由图7波形可以验证本文所设计的滑模观测器计算出的PMSM转子位置与实际PMSM转子位置相符,相位偏差得到了较好控制。
图8给出了电机转速n=300 r/min,负载转矩TL=3N·m的情况下,在0.5s时负载突变为6N·m时PMSM转速波形。

图8 负载突变时PMSM电机转速变换
从图8可以看出,当0.5 s负载突变时,转速约有0.02 s的波动,之后电机以给定转速运行,验证了整个控制系统有较好的鲁棒性。
4 实验分析
为了验证本方法的有效性与实践性,搭建了基于TMS320F28335型号DSP处理器的PMSM实验平台,电机参数与表1一致。
图9和图10分别给出了PMSM以转速n=300 r/min运行时,空载时采用传统滑模观测器和优化型滑模观测器得到的反电动势波形。

图9 空载时采用传统滑模观测器反电动势实验波形
从图9可以看出,PMSM运行在空载低转速工况下,传统滑模观测器存在抖振现象。

图10 空载时采用优化型滑模观测器反电动势实验波形
从图9和图10对比可以看出,优化型滑模观测器在空载低转速情况下有效消除了抖振现象,得到的反电动波形没有发生畸变。
图11和图12分别给出了PMSM在转速n=300 r/min满载运行时,分别采用传统滑模观测器和优化型滑模观测器输出的实验波形。

图11 满载时采用传统滑模观测器反电动势实验波形

图12 满载时采用优化型滑模观测器反电动势实验波形
PMSM运行在低速满载工况下,传统滑模观测器输出值畸变、毛刺较为严重,滑模抖振明显。从图12可以得出,相同工况下,采用优化型滑模观测器的输出值,接近PMSM实际反电动势,波动明显弱很多。
5 结 语
本文研究了一种基于优化型滑模观测器的PMSM换相控制方法,该方法可以应用于无位置传感器控制系统中,并通过仿真和实验得到了验证。优化型滑模观测器得到的反电动势观测值较为精准,很大程度上削弱了抖振;整个控制系统不易受参数变化影响,在负载突变的情况下仍然可以稳定运行,准确、快速实现电机控制,整个电机控制系统具有较高的稳态精度,具有一定的应用价值。

