滚转舰炮制导炮弹的空间多约束导引与控制一体化设计

姜尚，田福庆，孙世岩，梁伟阁

海军工程大学 兵器工程学院，武汉 430033

近年来，高新技术的迅猛发展与“前沿作战，从海到陆，由海制陆”、“超视距登陆”等海战思想的发展进步，要求舰炮武器具备对海对岸的持续火力支援与精确打击能力[1]。舰炮制导炮弹是低速滚转弹药，比导弹射速高、携弹多、持续久，较传统弹药射程远、精度高、效费比高，能够有效地对近岸固定或机动目标实施远程压制与高效毁伤，为两栖作战部队提供坚实可靠的海上火力支援[2]。

末端导引控制方法是事关舰炮制导炮弹执行作战任务成败的核心技术。攻防装备体系的升级与弹体的高速飞行使导引与控制系统的各状态变化剧烈，而且相对于导弹、高超声速飞行器等高速运动的非滚转类飞行器，其连续滚转特性进一步增强了质心导引与姿态控制之间、俯仰与偏航通道之间的耦合作用，导致作用在弹体上的力与力矩同导引与控制两子系统的状态紧密相关[3]，外加目标机动、风与建模误差等不确定性因素的干扰，都增强了弹体动力学与运动学模型、弹目相对运动模型的非线性程度。因此，需要以导引与控制系统的传统分离设计方法为基础，充分考虑导引与控制系统之间的耦合特性以及连续滚转特性，进行导引与控制一体化(Integrated Guidance and Control，IGC)设计。为达到更好的毁伤效果，需要充分考虑实战中存在的约束条件，如攻击角、舵机角度受限与视线角速率测量受限[4]，这促使着国内外专家学者与工程人员研究满足多约束条件IGC的设计方法。

Williams等[5]突破传统的时标分离设计方式，首次提出了IGC概念，其本质是运用导引与控制系统间的耦合关系，通过气动角构建出两者的直接联系，形成一个串级型闭环系统，通过控制算法根据弹目相对运动与弹体运动信息直接解算出舵机控制指令。自此，众多学者结合最优控制[6]、鲁棒控制[7-8]、反步动态面控制[9-10]、自适应控制[7-9]、滑模控制(Sliding Mode Control, SMC)[11-14]等现代控制理论取得了丰硕成果。最优控制需要求解复杂的Hamilton-Jacobi-Bellman方程，Vaddi等[6]基于非线性最优控制提出了一种IGC设计方法，将线性控制在非线性系统设计方面进行了扩展，提高了IGC性能，但并未考虑其他约束条件。杨靖等[7]针对远程制导炮弹提出了基于滑模观测器的鲁棒IGC方法，建立了包含舵机一阶动态特性的平面模型，引入自适应鲁棒项对观测误差进行镇定，但依赖于视线(Line of Sight,LOS)速率的精确测量，这对滚转弹提出了过高的要求。反步控制需要求解虚拟控制量的高阶导数，容易导致微分膨胀问题，为此，周觐等[9]设计动态面并引入低通滤波器，避免了微分膨胀，在保证末制导性能的前提下简化了设计过程。进一步地，张尧等[10]结合扩张状态观测器(Extended State Observer, ESO)设计动态面反步控制器，通过ESO观测出建模误差、气动参数摄动等不确定干扰，明显减小了动态面的切换幅度，由于未处理观测误差项，在系统稳定性证明方面有待完善。韩京清[15]首次提出算法结构简单的ESO，在缺乏对象精确模型的工况下，能同时精确地观测出系统状态与内外部干扰[16]，适用于解决具有时变性、非线性、耦合性以及多不确定性的IGC问题。值得注意的是，作为制导炮弹的唯一执行机构，鸭舵常常出现偏转饱和现象，使可用过载小于需用过载，容易导致系统失控失稳，受文献[8]启发，通过设计自适应Nussbaum增益函数，对控制受限引发的饱和非线性进行有效地补偿，并结合自适应动态面控制较好地镇定串级系统。

SMC使非线性动态系统沿预先设计的滑模面运动，对模型参数摄动及外界干扰等失稳因素具有较强的鲁棒性，已广泛应用于IGC设计中。Shtessel和Tournes[11]将目标机动产生的法向加速度视为一种干扰。设计了基于非线性动态滑模流形的高阶滑模IGC方法，对目标机动和导弹模型不确定性均具有较强的鲁棒性。Wu和Yang[12]针对导弹受终端攻击角约束的要求，将攻击角定义为弹速与水平面的夹角，通过非线性变换将其转化为适合SMC的标准形式，提出了一种IGC设计方案。但文献[13]指出，将攻击角定义为命中时刻的弹目速度夹角更具有普遍意义，可以将攻击角约束转换为终端视线角约束。进一步地，Guo和Liang[14]结合块动态面、滑模控制与ESO设计了IGC，使非滚转近空拦截器获得了较好的制导性能，但这并不适用于滚转类飞行器。

滚转特性显著增强了舰炮制导炮弹俯仰、偏航通道之间的耦合关系，而现有文献对IGC的研究基本上是聚焦于空间或平面内单约束的非滚转类飞行器，目前尚未参阅到有关滚转类飞行器IGC设计的文献，多约束更是给系统的有限时间收敛性与稳定性带来了不小的挑战，但这恰恰是作战中存在且亟待解决的问题，因此，本文充分考虑上述因素，全面地考虑了包括风速在内的各类干扰因素，构建了适用于滚转制导炮弹的严块反馈IGC串级模型，提出了基于块动态面与ESO(Block Dynamic Surface Extended State Observer, BDSESO)的IGC设计方法，通过Lyapunov理论证明了LOS误差与LOS速率能在有限时间内收敛，全系统状态一致最终有界且任意小，主要创新点为：① 设计ESO准确快速地观测出LOS速率与系统内外不确定性干扰，设计块动态面，避免了微分膨胀并简化了虚拟控制量的求解过程；② BDSESO方法在保证较小脱靶量的同时满足攻击角、鸭舵控制受限、视线角速率测量受限等多约束条件；③ 结合型号产品，通过自主设计的半实物仿真实验系统，验证了BDSESO方法的有效性与可行性。

1 模型建立

1.1 运动与力学模型

空间弹目相对运动如图1所示，Px0y0z0、Px2y2z2、Px6y6z6、Tx7y7z7、Tx8y8z8分别表示弹体基准坐标系(NP)、弹道坐标系(PV)、视线坐标系(QS)、目标基准坐标系(NT)、目标弹道坐标系(TV)，P、T、R、θQ、ψQ分别表示制导炮弹、目标、弹目距离、视线倾角、视线偏角，θP、ψP、vP、vP、θT、ψT、vT、vT分别表示弹体与目标的弹道倾角、弹道偏角、速度矢量、速度大小。

图1 空间弹目相对运动

定义θ、ψ、γ、α、β、δz、δy分别表示俯仰角、偏航角、滚转角、攻角、侧滑角、俯仰舵角、偏航舵角，详情参阅文献[17]，本文仅符号表示不同，坐标系转换、力以及力矩等部分的分析原理相同。α、β、δz、δy随弹体滚转而周期性变化，因此，研究滚转制导炮弹还需要建立非滚转的准弹体坐标系Px4y4z4、准速度坐标系Px5y5z5，定义准攻角α*、准侧滑角β*、等效俯仰舵角δzeq、等效偏航舵角δyeq来计算滚转弹的各项力与力矩，它们之间的转换关系为

(1)

(2)

假设1[7]视P为刚体、T为质点，R、θQ、ψQ、θP、ψP、vP、θ、ψ、γ易通过现有技术手段测得，P、T仅在速度法向有加速度，且始终满足vP>vT。

Px2y2z2系向Px6y6z6系变换的转换矩阵为

(3)

弹目相对运动关系为

(4)

式中：[aPx6,aPy6,aPz6]T、[aTx6,aTy6,aTz6]T分别为弹体加速度aP、目标加速度aT在Px6y6z6系上的分量；r为R在偏航平面的投影，定义aP在Px2y2z2系上的分量为[0,aPy2,aPz2]T、aT在Tx8y8z8系上的分量为[0,aTy8,aTz8]T；dθT、dψT为目标机动产生的未知干扰；aP由Px2y2z2系向Px6y6z6系的转换关系为

(5)

式中：daPy、daPz为坐标转换产生的误差干扰，同理易得aT由Tx8y8z8系向Px6y6z6系的转换关系。作用在弹体的合外力FP主要由重力G、全弹升力Ry、马格努斯力Rz、等效操纵力Fδeq、干扰风力Fw组成，FP在Py2、Pz2轴的分量分别为法向力FPy2、侧向力FPz2；合外力矩M主要由静力矩Mz、赤道阻尼力矩Mzz、马格努斯力矩My、等效操纵力矩Mδeq、风干扰力矩Mw及建模误差组成，M在Pz4、Py4轴的分量为俯仰力矩Mz4、偏航力矩My4，它们的计算公式为

(6)

(7)

(8)

(9)

(10)

(11)

为便于IGC的设计，作合理假设如下，

假设2[12]FPy2、FPz2主要由α*、β*产生，δzeq、δyeq产生的力占比重较小，可视为有界不确定干扰。

由弹体绕质心转动动力学与运动学方程可得

(12)

(13)

将舵机的延迟特性视为具有舵机常数τc的一阶惯性环节，综上可得滚转舰炮制导炮弹的空间IGC模型为

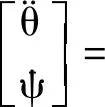
(14)

1.2 近岸机动目标模型

近岸机动目标由一阶惯性环节描述为

(15)

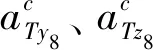
1.3 攻击角模型

在俯仰平面，攻击角ϑE为命中时刻弹目速度夹角，通过零化弹目相对法向速度可得[4]

(16)

式中：θQf、θTf为命中时刻的视线倾角、目标弹道倾角，由于近岸地形较为平坦且可以在战前通过无人侦察获取，θTf可视为已知，即对于任一给定的ϑE，都存在唯一的终端视线倾角θQf与之对应，那么俯仰与偏航平面上的攻击角约束问题就可以转换为θQ、ψQ的约束问题。

1.4 系统状态空间

定义系统状态变量、输入变量、输出变量为

(17)

为便于IGC的设计，引入一种连续可微的双曲正切函数向量g(x5)来描述舵偏饱和：

(18)

(19)

综合上述，可以得到滚转舰炮滚转制导炮弹的空间IGC的严块反馈状态空间为

(20)

式中：d4=d40+a4[satm(x5)-g(x5)]，为便于IGC的设计，作合理假设如下：

2 BDSESO设计

设计BDSESO目的：针对IGC系统(19)，在状态变量x2测量受限、x5控制饱和受限、干扰项di未知有界的情况下，设计BDSESO产生u，使x1、x2在有限时间内收敛至零点的任意小邻域内，并保证全系统状态一致最终有界任意小。

2.1 ESO设计

为了对d2进行观测，现定义观测变量为zx1=[zx11,zx12]T，zx2=[zx21,zx22]T，zd2=[zd21,zd22]T，建立ESO为

(21)

作者已在文献[4]中对在串级系统中设计的2阶、3阶ESO的稳定性进行了推导与证明，因此可知，无论干扰项d2是否连续，只要选择合适的参数，令β23ii远大于β22ii、β21ii，就可以进行精确快速地观测，即zx1→x1、zx2→x2、zd2→d2。同理，为观测di(i=3,4,5)，定义观测变量为zxi=[zxi1,zxi2]T，zdi=[zdi1,zdi2]T，建立ESO为

(22)

(23)

(24)

2.2 非奇异终端滑模设计

引理1[14]考虑如下系统：

(25)

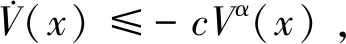
选用一种非奇异终端滑模构造滑模面向量：

(26)

式中：0<μj；1<δj<2。求导可得

[f2+a2x3+d2]

(27)

为保证滑模在趋近过程中具有良好的动态品质，设计滑模自适应趋近律为

(28)

(29)

定理1由系统(20)前两个等式构成的子系统，采用ESO式(21)与控制指令(29)，x1、x2能在有限时间内收敛至零点的任意小邻域内。

(30)

显然，当x2≠0时，由Lyapunov稳定性定理可知，非奇异终端滑模s2可在有限时间内收敛至滑模面s2=0，这一结论当x2=0时同样满足[18]，此后

(31)

(32)

由引理1可知，状态变量x1、x2能在有限时间内收敛至零点的任意小邻域内，定理1证毕。

2.3 块动态面设计

步骤1定义s2为块动态面2。

(33)

式中：τ3>0为低通滤波器常数。

步骤2定义块动态面3为

s3=x3-x3d

(34)

求导得

(35)

(36)

(37)

步骤3定义块动态面4为

s4=x4-x4d

(38)

(39)

(40)

步骤4定义块动态面5为

s5=g-gd

(41)

求导得

(42)

为有效地处理由鸭舵偏转饱和导致的控制受限问题，设计控制量为

(43)

(44)

选取Nussbaum函数，并设计其自适应律为

(45)

(46)

3 稳定性分析

引理2[20]对任意给定的一阶线性非齐次微分方程dy/dt+P1(x)y=Q1(x)，其通解形式为

(47)

式中：C为任意常数。

(48)

则函数V(t)与χ(t)在定义域上必有界，式中C>0、M>0。

定义虚拟控制量误差为

(49)

求导可得

(50)

进一步推导可得

(51)

(52)

选取全系统Lyapunov函数V:

(53)

定义动态面向量为s=[s21,s22,...,s51,s52]T，并定义其范数为

(54)

(55)

证明对V求导，可得

(56)

令正常数ε=min{mij}(i=1,2,...,7;j=1,2)，取正常数为ζ=3ρ2/2，则式(56)可化为

(57)

由引理2可得式(57)的解满足如下不等式：

(58)

根据引理3与Barbalat引理可知，全系统Lyapunov函数V与系统状态一致最终有界且任意小，进一步地，由式(57)可得

(59)

由式(58)可得

V(T1)-V(0)≤V(T1)-V(0)e-2εT1≤

(60)

联立式(58)和式(60)可得

(61)

定理2证毕。为了有效地削弱变结构项导致的控制量抖振，通常采用连续的饱和函数向量satsi=[satsi1,satsi2]T(i=3,4,5)代替符号函数向量，sat(·)=·/(|·|+δ)，δ>0。

4 实验验证与分析

为了验证所提出BDSESO的有效性与可行性，实验选取某型舰炮制导炮弹的控制舱为被控对象，搭建半实物仿真系统如图2所示，主要包括控制舱(含微控制器、某型双通道舵机)、上位机、三轴转台、工控机，设备间的通讯类型和传输方式已标明。舵机与转台的主要性能指标如表1和表2所示，均满足半实物仿真要求。

系统的核心部件是STM32F429IGT6微控制器，它根据在Keil中编译的程序配置RS232总线通讯、中断、DMA与ADC等功能。上位机通过向控制舱发送控制指令控制系统的初始、启动、停止与恢复等状态，启动仿真后，微控制器采用卡尔曼滤波在线处理ADC采集的舵偏反馈，获取工控机的姿态反馈，并使用反馈参量通过四阶龙格库塔法以10 ms步长循环迭代微分方程组(由弹体六自由度方程、目标三自由度方程、相对运动方程与IGC设计方法等构成)，解算出对应参量回传上位机，同时将舵偏指令、姿态指令分别发送给双通道舵机、工控机，工控机根据姿态指令驱动转台，并将转台姿态反馈至控制舱，当弹目距离小于杀伤半径时仿真停止。为保证微控制器解算程序的效率和设备间通讯的实时性，对数据量较大的链路采用DMA方式传输。

图2 半实物仿真系统

表1 舵机的主要性能指标

表2 转台的主要性能指标

确定弹体参数、运动与系统参数、导引与控制参数，如表3～表5所示。为体现BDSESO无需视线角速率信息反馈，式(29)、式(36)、式(39)、式(44)中均使用zx2信息，导引头盲区为50 m，在盲区内舵机指令不变，制导炮弹依靠惯性飞行。分别在打击正弦和方波机动目标的工况下，对BDSESO进行半实物和数字仿真，作为对比，在相同工况下对文献[20]中的ADSC(Adaptive Dynamic Surface Control)方法进行数字仿真，受篇幅所限，仅展示部分结果。

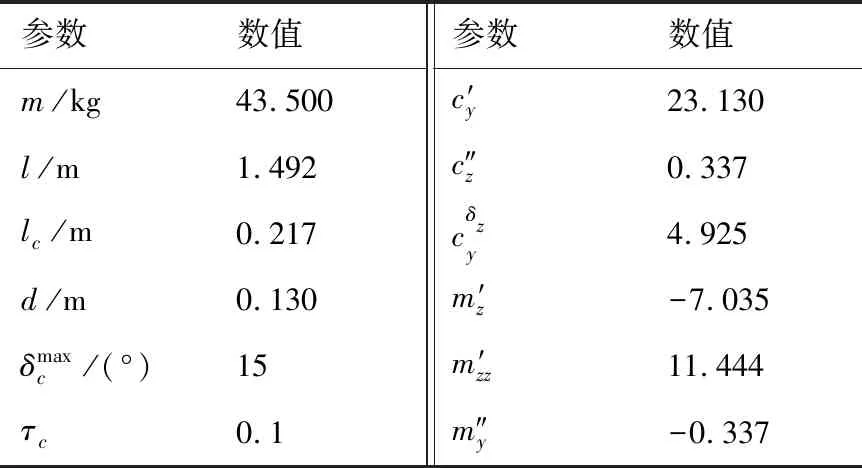
表3 弹体参数

表4 运动与系统参数

4.1 工况1：正弦机动目标

设定正弦机动目标的加速度指令为

(62)

实验结果如表6与图3所示。图3(a)为弹目运动轨迹，BDSESO、ASDC均可使制导炮弹命中正弦机动目标，结合表6可看出较ASDC，BDSESO的弹道更为平直，进一步改善了脱靶量、命中时间与终端角误差，并且受干扰因素的影响较小，具备良好的鲁棒性。由图3(b)可知法向过载的变化情况，因系统干扰项未得到有效处理，给仅采用自适应鲁棒项的ASDC调控带来较大的压力，使其过载峰值与变化范围均明显大于BDSESO，而后者通过有机结合ESO与块动态面，控制指令的变化较为平滑，并在终点附近有收敛趋势，这更加符合实际作战需求。准攻角的变化趋势如图3(c)所示，它与法向过载基本一致，侧面说明了假设2的合理性，ASDC在末制导初段突变情况更为严重，且受通道耦合与风速等因素的干扰较大，不利于制导炮弹的稳定飞行，而BDSESO在ESO与块动态面的配合调控下，准攻角峰值较小且保持着较低的变化程度。由图3(d)可知等效俯仰舵偏角的变化趋势接近于法向过载，通过引入自适应Nussbaum函数，BDSESO有效降低舵机指令的峰值，尽量避免了制导炮弹因舵偏饱和而导致的作战任务失败。分析图3(e)得知，型号舵机的俯仰通道能够满足实际俯仰舵偏角在切换频率与幅度等方面要求，BDSESO控制时的变化范围与突变情况均优于ASDC。视线倾角速率如图3(f)，在BDSESO的调控下，视线倾角速率自8 s后能较稳定地保持收敛状态，表明系统状态变量x1、x2能在有限时间内收敛至0，验证了对非奇异终端滑模进行的有限时间收敛性分析的正确性。图3(g)表明弹体的俯仰角变化是平滑连续的，BDSESO的收敛速率快于ASDC，且超调较小，同时也验证了转台俯仰通道具有良好的随动性能以及控制舱对其进行控制的实时性。图3(f)、图3(h)、图3(i)表明ESO具有良好的观测性与鲁棒性，能快速准确地提供视线倾角速率与不确定干扰，为有效命中正弦机动目标提供了重要的信息，使制导炮弹能提供足够可用的过载指令补偿不确定干扰对制导性能的负面影响，降低了对制导炮弹硬件层面的要求。

表6 工况1实验结果

4.2 工况2：方波机动目标

设定方波机动目标的加速度指令为

(63)

实验结果如表7与图4所示。图4(a)为弹目运动轨迹，BDSESO、ASDC均可用于制导炮弹攻击方波机动目标的末制导段，结合表7可知，BDSESO优化了脱靶量、命中时间与终端角误差，且其弹道较为平直，各类不确定干扰因素对弹道曲率的影响也较小，有利于制导炮弹在末制导过程中进行精细调节。图4(b)描述了侧向过载的变化趋势，由于ASDC未有效处理系统干扰项，仅靠自适应鲁棒项镇定系统，导致其过载变化大、峰值较大且末端收敛速率较慢，而BDSESO在末制导过程中均较为平滑，且末端收敛速率较快，体现出良好的鲁棒性。由图4(c)可知，准侧滑角的变化与侧向过载基本一致，较好地印证了假设2的正确性，相比于ASDC，BDSESO在ESO与块动态面的调控下，准侧滑角峰值较小、变化较缓，能够适应存在各类不确定干扰的工况。由图4(d)可知，ASDC未考虑舵偏饱和受限的约束，等效偏航舵偏角峰值较大、舵偏速率较快，容易出现饱和现象，这往往会浪费有限的能量、贻误作战时机，甚至对舵机造成不可逆损害，而BDSESO通过引入自适应Nussbaum增益函数却可以有效地降低舵偏指令峰值与舵偏速率。分析图4(e)得知，型号舵机的偏航通道能够满足实际偏航舵偏角在切换频率与幅度等方面要求，在BDSESO的调控下，其变化范围与突变情况均优于ASDC。从图4(f)分析可知，由于通道耦合因素对偏航通道的影响明显大于俯仰通道，导致视线偏角速率的收敛速度慢于视线倾角，由于未处理系统干扰项，ASDC受干扰影响更大，甚至在命中时也未达到收敛状态，而BDSESO通过ESO与块动态面在14 s后能使视线偏角误差、视线偏角速率收敛至零，表明所设计的非奇异终端滑模是有限时间收敛的。由于受通道耦合影响较大，在初始阶段ESO并不能完全观测出不确定干扰d42，造成图4(g)中的偏航角变化较为明显，随后便以较快的速度进入连续平滑的变化状态，从另一个角度来看，更能够说明转台的偏航通道具有良好的跟踪特性。图4(f)、图4(h)、图4(i)体现出ESO良好的观测性与鲁棒性，即使在综合干扰项变化较快、范围较大的工况下也能快速准确地观测出视线偏角速率与干扰，提供准确的必要的反馈信息，减少了控制舱的硬件传感元件。

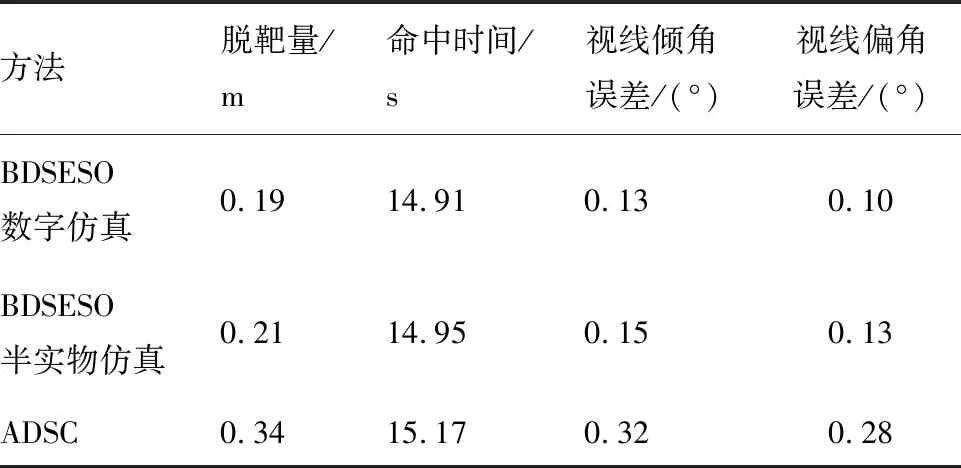
表7 工况2实验结果

图4 工况2实验曲线

5 结 论

针对大口径舰炮制导弹药打击近岸机动目标的末制导段，设计了BDSESO方法，经模型建立、理论证明与半实物仿真实验，在打击机动形式不同的目标时，均具备较好的末制导性能，现总结全文如下：

1) 较为全面地考虑了包括风速在内的各类干扰因素，构建了适用于滚转舰炮制导炮弹的严块反馈IGC串级模型。

2) ESO准确快速地观测出视线角速率与系统内外不确定性干扰，设计块动态面既避免了微分膨胀又简化了虚拟控制量的求解过程。

3) 严格地证明了视线角跟踪误差与视线角速率的有限时间收敛性与全系统状态一致最终有界性，无需测量视线角速率信息，降低了硬件层面的要求。

4) 结合型号产品，通过自主设计的半实物仿真实验系统，较好地验证了BDSESO的有效性与优越性，具有一定的理论与工程价值。