带筋整体壁板预应力喷丸成形数值模拟及变形预测

田硕，尚建勤,*，盖鹏涛，陈福龙，曾元松

1. 中国航空制造技术研究院，北京 100024

2. 塑性成形技术航空科技重点实验室，北京 100024

3. 数字化塑性成形技术及装备北京市重点实验室，北京 100024

随着现代飞机性能的不断提高，具有优异结构效率、减重效益和密封效果的带筋整体壁板在新一代大型飞机上的应用越来越广[1]。喷丸成形技术在国内外被广泛应用于金属机翼等航空航天器整体壁板的成形，预应力喷丸成形技术是大中型、长寿命、高性能带筋整体壁板尤其是复杂双曲外型带筋整体壁板(包含不带筋整体壁板)的一种不可多得的有效成形手段[2-5]。数值模拟技术，具有部分替代实物试验、缩短研发周期、降低研发成本等显著优点，是促进带筋整体壁板预应力喷丸成形技术研究、进步与应用的一种极具潜力的途径。

针对预应力喷丸成形技术，国内外学者进行了广泛研究。文献[6]通过喷丸成形工艺试验研究了平板件预弯量与弧高值间的关系。文献[7]中空客A310和阿丽亚娜4型运载火箭带筋壁板零件采用预应力喷丸成形。文献[8]研究了不同预应力状态下钛基复合材料喷丸后残余应力分布情况。

随着计算机模拟技术的发展，数值模拟技术逐渐应用到预应力喷丸成形技术研究中。文献[9]提出了三步模拟法，对平板件预应力喷丸成形进行了模拟，并建立预弯量与弧高和残余应力分布之间的关系，最后通过试验进行了验证。文献[10]通过静压模型研究了平板件预应力喷丸成形过程，该模型能够预测不同工艺参数下的平均成形力，并能够进一步预测喷丸成形后的零件形状。文献[11]通过应力场法模拟金属机翼带筋壁板自由状态喷丸成形。文献[12]通过施加固有应变模拟平板件喷丸变形。

人工智能系统如人工神经网络具有优良的非线性映射能力以及对复杂不确定系统具有自适应和自学习能力，近年来逐渐应用于工程问题的预测和优化等[13]。文献[14]根据喷丸强化试验结果，利用BP神经网络建立了残余应力预测模型，并试验验证了其准确性。文献[15]建立了TC17合金高能喷丸处理后表层显微硬度的模糊神经网络预测模型。文献[16]中以平板件喷丸变形由表层延展变形和整体弯曲变形组成为条件，通过建立喷丸工艺参数与延展应变和弯曲曲率之间的BP神经网络模型，实现了机翼整体壁板喷丸成形工艺参数的预测。BP神经网络属于全局逼近网络，耗时多、迭代步数长、易陷入局部最优；RBF神经网络是局部逼近网络，具有学习速度快，不会陷入局部最优的特点；因此文献[17]建立了预测喷丸成形工艺参数的RBF神经网络模型，并试验验证了其有效性。

目前，预应力喷丸成形数值模拟的研究对象主要集中在平板件，针对带筋整体壁板预应力喷丸成形数值模拟的研究还未见报道。本文针对带筋整体壁板预应力喷丸成形数值模拟，首先构建基于响应面函数的多弹丸撞击有限元模型，其次构筑基于应变中性层内移的反弯曲应力场法模拟模型，开展预应力喷丸成形数值模拟分析研究及试验验证，然后建立预应力喷丸弯曲变形与工艺参数之间的RBF神经网络预测模型，最终实现带筋整体壁板预应力喷丸成形的数值模拟及变形预测。

1 喷丸成形应力场法数值模拟

1.1 诱导应力

在喷丸成形过程中，弹丸撞击工件，在材料内部引入不平衡应力，产生材料流动，实现力的静态平衡，使受喷工件成形；由弹丸撞击在受喷工件材料内部产生的不平衡应力称为喷丸诱导应力，该应力具有使受喷工件材料产生延展和弯曲的趋势；喷丸撞击之后仍然保留在材料内部的应力称为喷丸残余应力；上述残余、诱导、轴向和弯曲4种应力之间的关系[18-19]为

σr=σi+σa+σb

(1)

式中：σr为喷丸残余应力；σi为喷丸诱导应力；σa为与均匀拉伸有关的轴向应力；σb为与纯弯曲有关的弯曲应力。

1.2 应力场法数值模拟

应力场法喷丸成形数值模拟是指，将通过数值模拟获得的喷丸诱导应力以初始应力的形式引入代表工件的有限元壳单元中，进行有限元模拟分析，获得受喷工件最终变形结果的一种数值模拟方法，其过程见图1。

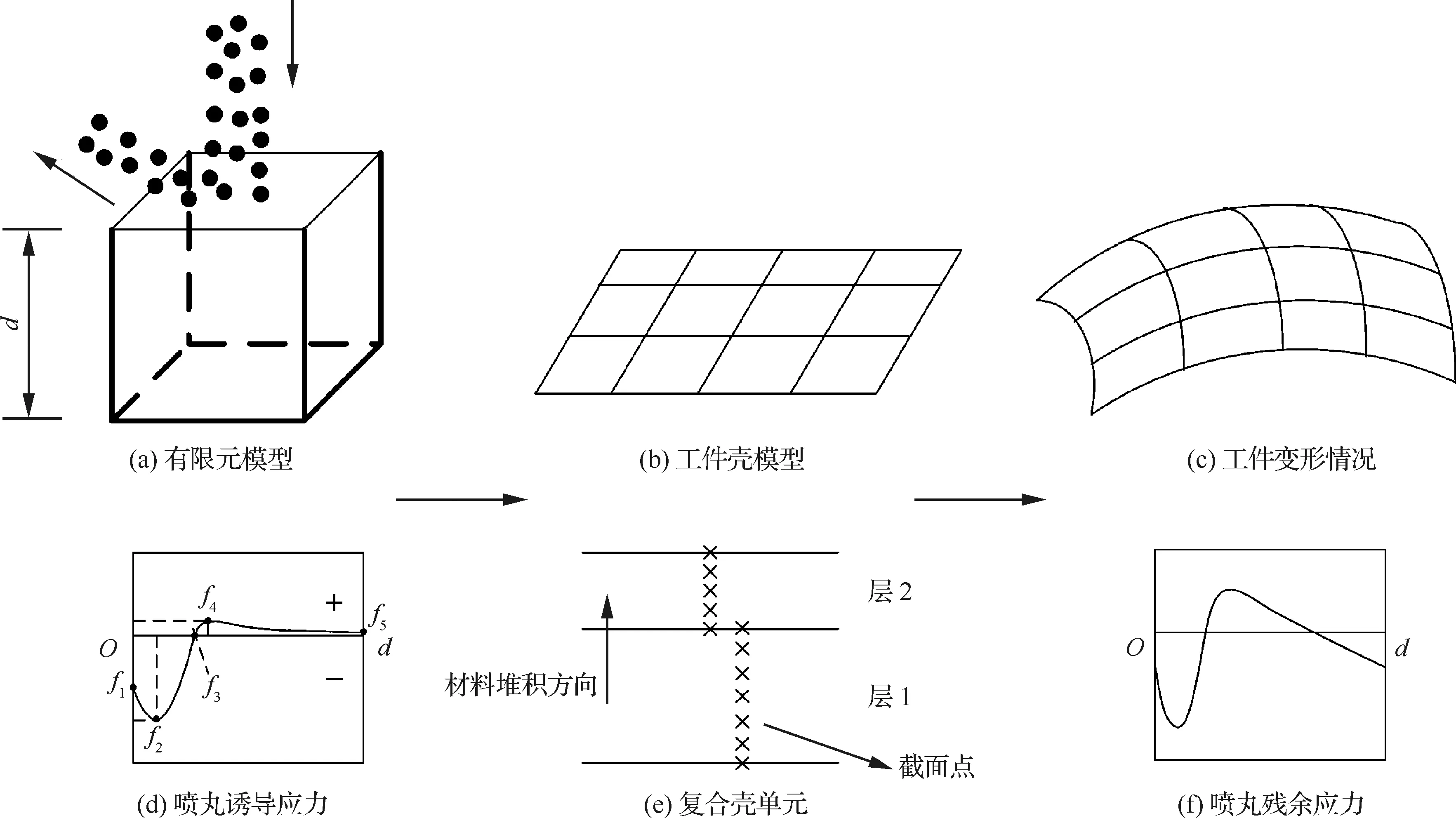
图1 喷丸成形应力场法数值模拟过程

图1(a)为多弹丸撞击有限元模型，在撞击过程中固定该模型所有非喷丸表面，然后对喷丸表面进行喷丸，此时模型内部的应力即为喷丸诱导应力(见图1(d))，由5个特征点fi(li,σi)(i=1,2,3, 4,5)构成，其中fi、li、σi分别为第i个特征点的标记、距表层深度和应力。图1(b)为代表工件的有限元壳模型。图1(e)为施加应力场所需的复合壳单元，层1和层2的厚度之和即为图1(a)中模型厚度d。在ABAQUS软件中，沿厚度方向的每一个截面点(或称积分点，Section Points)独立地计算应力应变值，因此通过关键字命令将图1(d)中的诱导应力赋予图1(e)中同一厚度处的截面点上。在软件中，对已经引入诱导应力的工件壳模型进行计算，得到工件喷丸变形结果，见图1(c)；此时工件内部仍保留的应力即为喷丸残余应力，见图1(f)。

研究表明，仅增大多弹丸模型(总)厚度(d≥2.5 mm)时诱导应力曲线呈现以下特点 见图2：

1) 各特征点距喷丸表层深度值几乎不变,见图2(a)。

2) 各特征点的应力值近乎不变,见图2(b)。

3) 底部应力逐渐减小；当模型(总)厚度大于某一数值之后，底部应力曲线基本稳定,见图2(c)。

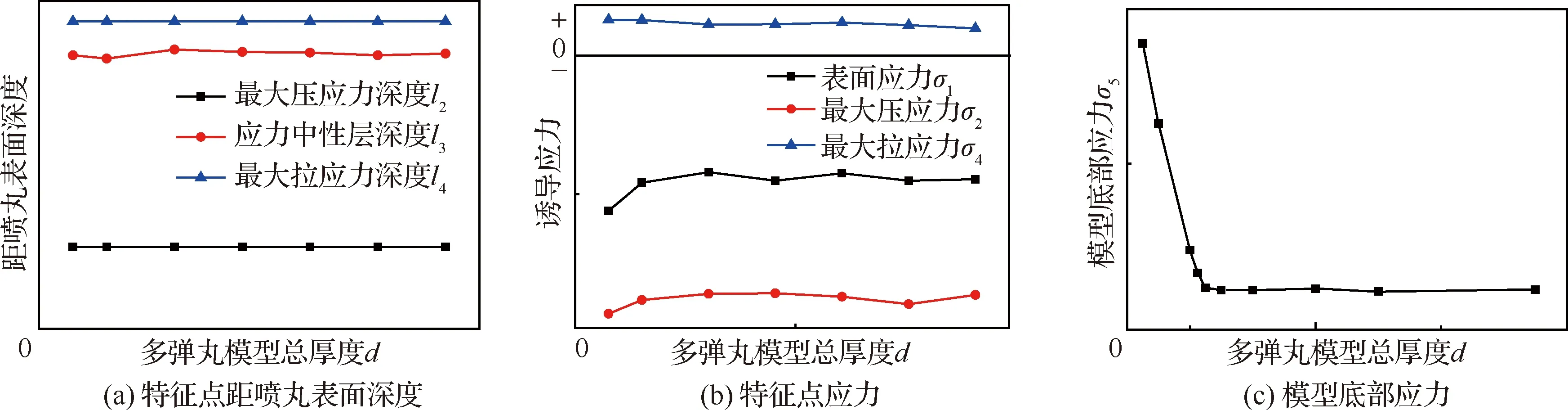
图2 模型总厚度对诱导应力的影响

1.3 响应面模型

由图1(a)可以看出，需要通过多弹丸撞击模拟模型获得应力场法模拟所需的诱导应力场，但是多弹丸撞击模型无法输入实际喷丸工艺参数，因此必须输入多弹丸撞击模拟参数；在弹丸的大小、材料及状态确定的条件下，模拟参数包括：弹坑直径D、弹丸速度V和覆盖率C，与喷丸工艺参数如喷丸气压p、弹丸流量q和进给速度s密切相关；本文通过喷丸试验及统计分析方法，建立模拟参数与工艺参数之间的响应面模型。

喷丸试验试验件：材料2024-T351铝合金、尺寸规格为150 mm×140 mm×8 mm平板件；喷丸设备：MP15000进口数控喷丸机；喷丸方式：自由状态单面喷丸；弹丸规格：∅3.18 mm铸钢丸；喷射角：90°；喷射距：300 mm；喷丸条带间距：70 mm。运用逐步回归法，建立喷丸模拟参数与工艺参数之间的响应面模型：

D=1.047 67-0.010 697 5q+1.024 28p2

(2)

V=26.227 3-0.538 814q+52.511 7p2

(3)

C=135.832-245.405p-4.475 63s-

6.665 79+20.462pq

(4)

1.4 多弹丸撞击模型

利用ABAQUS软件建立多弹丸撞击模型，根据模型的对称性，只需研究1/4模型 见图3，其表面尺寸为6 mm×6 mm，并对两个对称面作对称约束。针对弹性预应力喷丸成形预弯加载过程，预弯可看做纯弯曲，加载到位之后截面内预应力呈线性分布，并且依据预弯量可以计算其大小及分布；通过自定义场分布函数在面Z=6 mm上施加Z向沿Y轴线性分布的面力σ(Y)以代表预应力，施加预应力后约束1/4模型两个侧面及底面的所有自由度。约束侧面时，为了不影响喷丸区域的材料流动，模拟分析时喷丸区域表面大小为3 mm×3 mm，见图4。

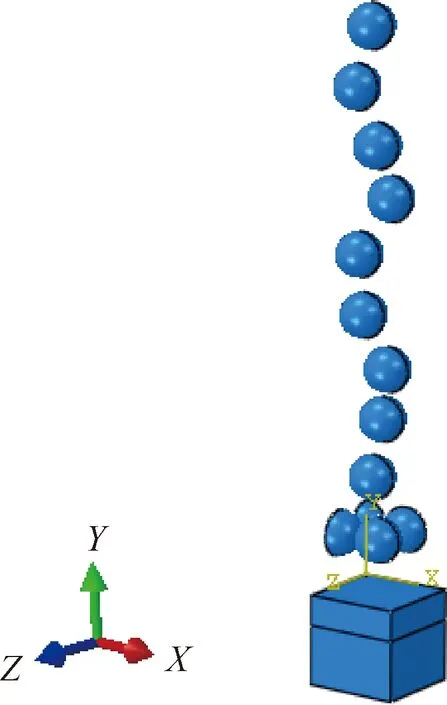
图3 多弹丸撞击模型

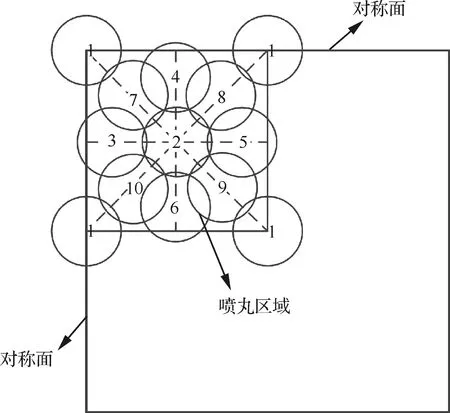
图4 弹丸的编号和撞击顺序及基准位置

由于实际喷丸成形时，覆盖率一般小于80%，因此所建模型对应的覆盖率范围为0～ 80%。为获得利用式(4)计算出的对应工艺参数的多弹丸撞击模拟参数——覆盖率，需预先对弹丸撞击位置及撞击弹丸数量进行规划，然后在装配模块对弹丸进行装配。如图4所示，圆圈代表弹坑，其中数字代表弹丸的编号及撞击模型的次序，弹坑直径利用式(2)计算。4个1号弹丸撞击基准位置为喷丸方形区域顶点，2号弹丸位于方形区域中心，3、4、5和6号弹丸撞击基准位置位于方形区域中位线上，且相距喷丸区域边界0.4 mm，7、8、9和10号弹丸位于对角线上，且相距喷丸边界均为0.75 mm。为获得精确覆盖率值，在图4基准位置的基础上，3、4、5和6号弹丸可以沿中位线向内外移动，7、8、9和10号可以沿对角线向内外移动。例如当p=0.35 MPa，q=12 kg·min-1，s=3 m·min-1时，利用式(2)和式(4)可算出D=1.045 mm，C=42.5%，由图5可知当位于基准位置的弹丸数量为7个时，覆盖率为36.9%，弹丸数量为8个时，覆盖率为45.8%；因此为获得42.5%的覆盖率，需要8个弹丸，但是5号弹丸需要沿着中位线向外移动一定距离，图5中覆盖率值通过CATIA软件测量计算。

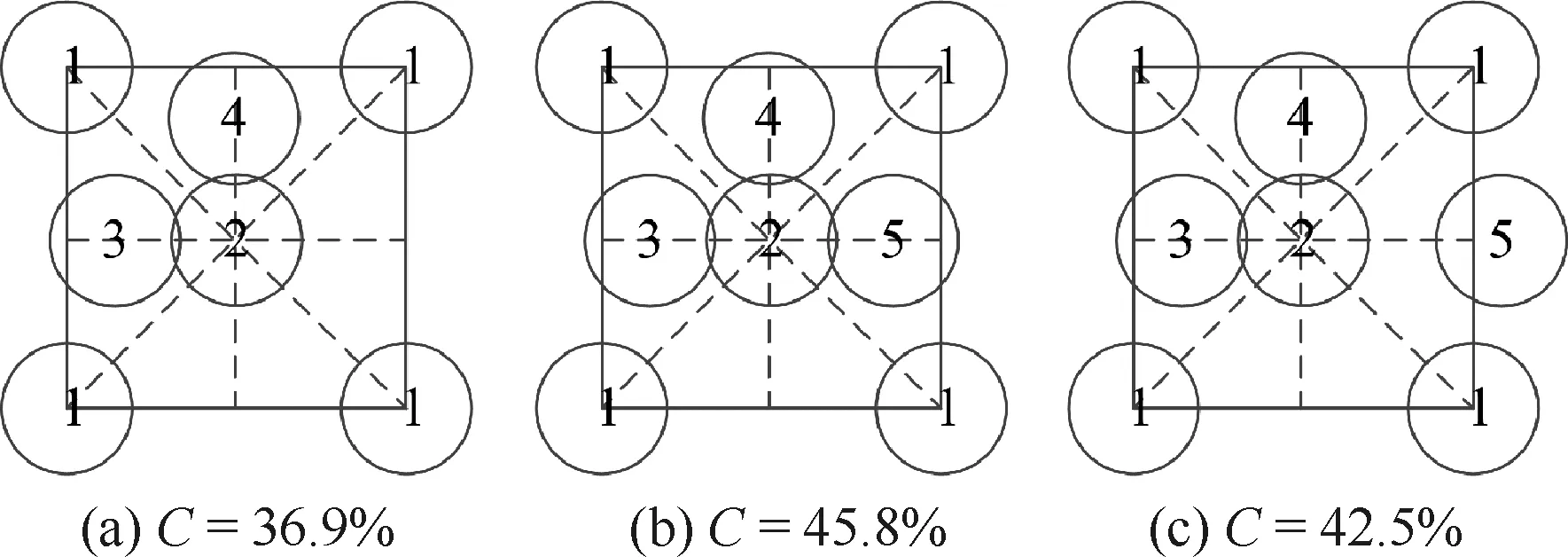
图5 撞击弹丸数量及位置规划

弹丸与模型间的接触算法为罚函数法，接触摩擦系数取为0.05，通过预定义场更改多弹丸撞击模拟参数——弹丸速度，该弹丸速度利用式(3)计算。弹丸设置成离散刚体，材料模型采用JC本构模型，受喷材料和材料本构模型参数见表1和表2[20]。

弹丸撞击结束，为了从模拟结果中方便地提取诱导应力，利用Python语言，对ABAQUS后处理进行二次开发，创建喷丸区域沿模型厚度方向的路径并获得路径节点应力，以便当改变模拟参数及软件重启时也能够快速获得所有路径上的应力值，对所有路径上同一厚度处的节点应力求平均值，即为相应工艺参数下该厚度处的诱导应力值；沿模型厚度方向，各个厚度处及其诱导应力值构成相应工艺参数下的诱导应力(场)[21]。

表1 材料参数[20]

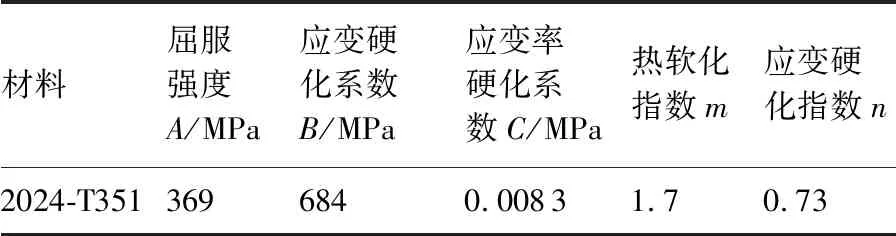
表2 材料本构模型参数[20]

基于响应面函数的多弹丸撞击模型，能够获得不同喷丸工艺参数下的诱导应力，因此可以实现应力场法对自由状态、预应力状态平板件及整体壁板(不包括带筋整体壁板)喷丸成形数值模拟，同时奠定了应力场法预应力状态带筋整体壁板喷丸成形数值模拟的必要条件。

2 带筋整体壁板预应力喷丸成形数值模拟

带筋整体壁板(见图6)可以看做是由若干典型单筋件组合而成，其喷丸成形难易程度与其典型单筋件喷丸成形难易程度密切相关，通常典型单筋件的喷丸成形工艺数据和变形规律是带筋整体壁板喷丸成形工艺分析、工艺方案制定及工艺参数确定的基本依据和基础。因此预应力喷丸成形数值模拟分析，首先针对单筋件进行，然后针对带筋整体壁板开展。

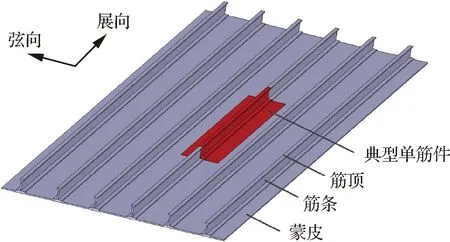
图6 带筋整体壁板机加板坯

2.1 反弯曲模拟模型

针对带筋整体壁板预应力状态喷丸成形特点，提出考虑中性层内移的反弯曲数值模拟模型，体现带筋整体壁板基本特征的典型单元件——单筋件预应力喷丸成形模拟过程如图7所示。

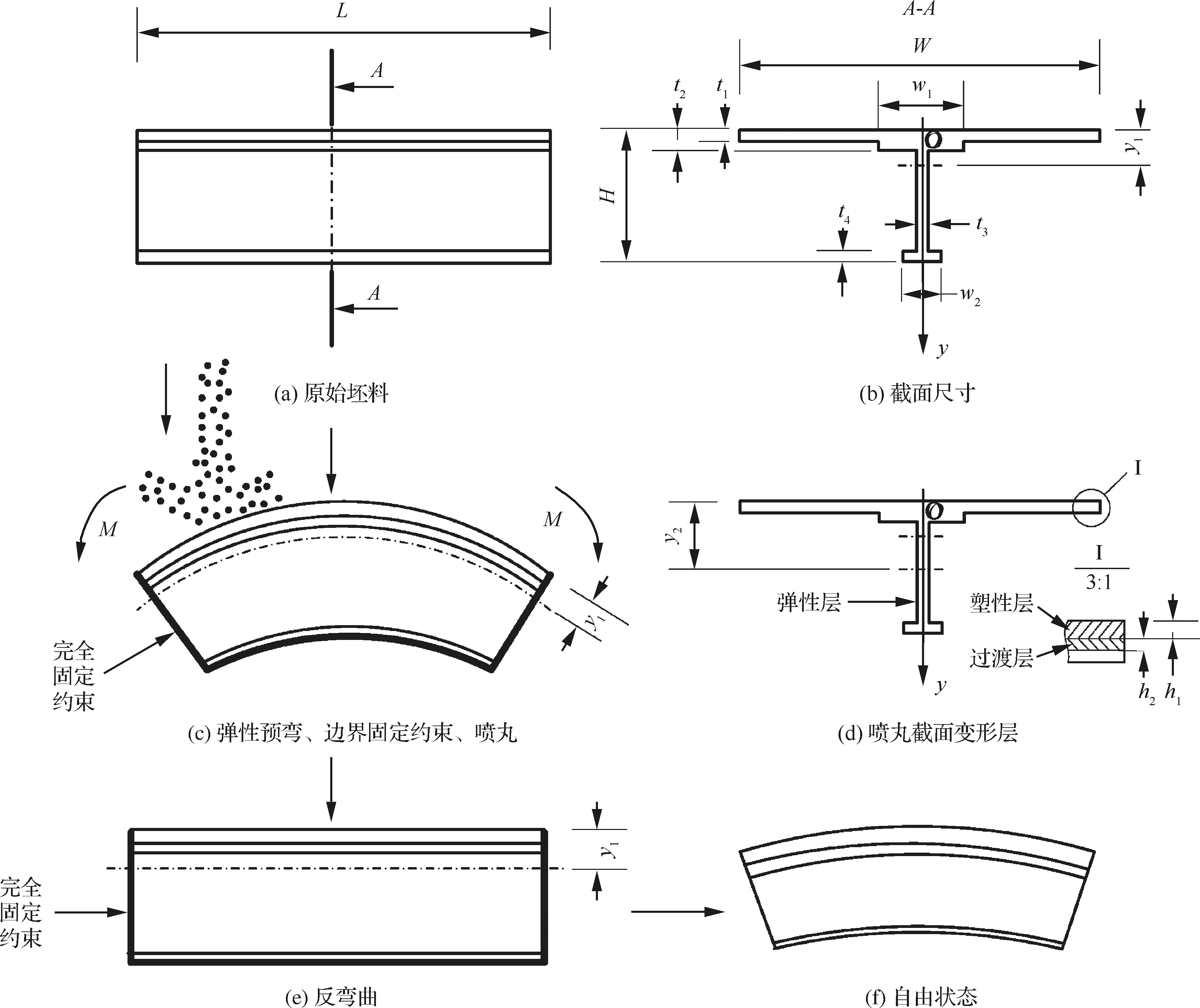
图7 反弯曲模拟过程

图7(a)为原始坯料，图7(b)为单筋件截面尺寸：L=1 340 mm，W=140 mm，w1=42 mm，w2=16 mm，t1=4.5 mm，t2=8 mm，t3=3.8 mm，t4=3.8 mm，H=56.9 mm。由图7(b)中所给截面尺寸可以计算出截面中性层高度y1=10.82 mm。图7(c)为边界固定条件下的喷丸过程。

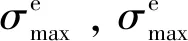
(5)

式中：E为弹性模量；R为弹性预弯半径。

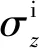
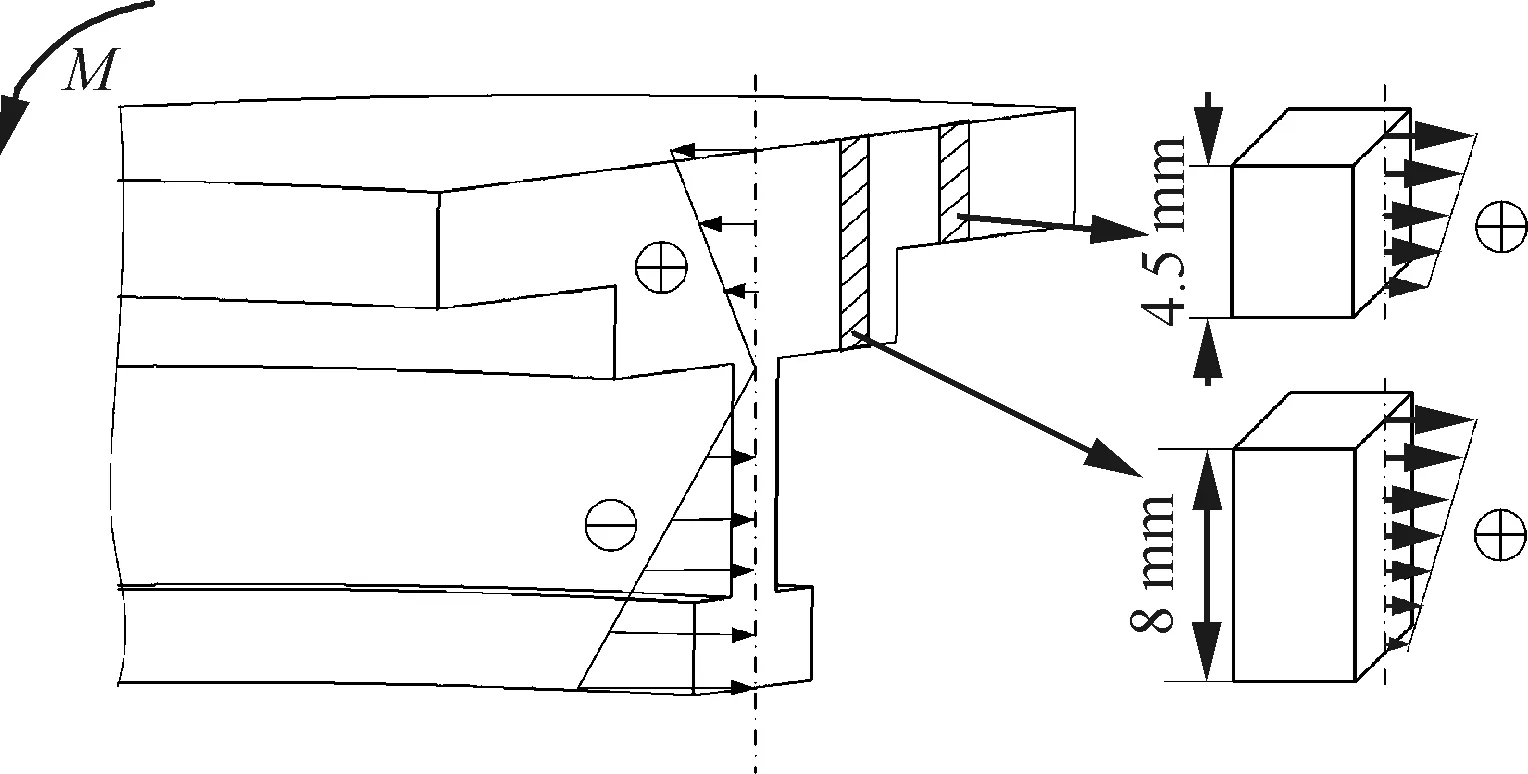
图8 预弯状态下单筋件截面应力分布

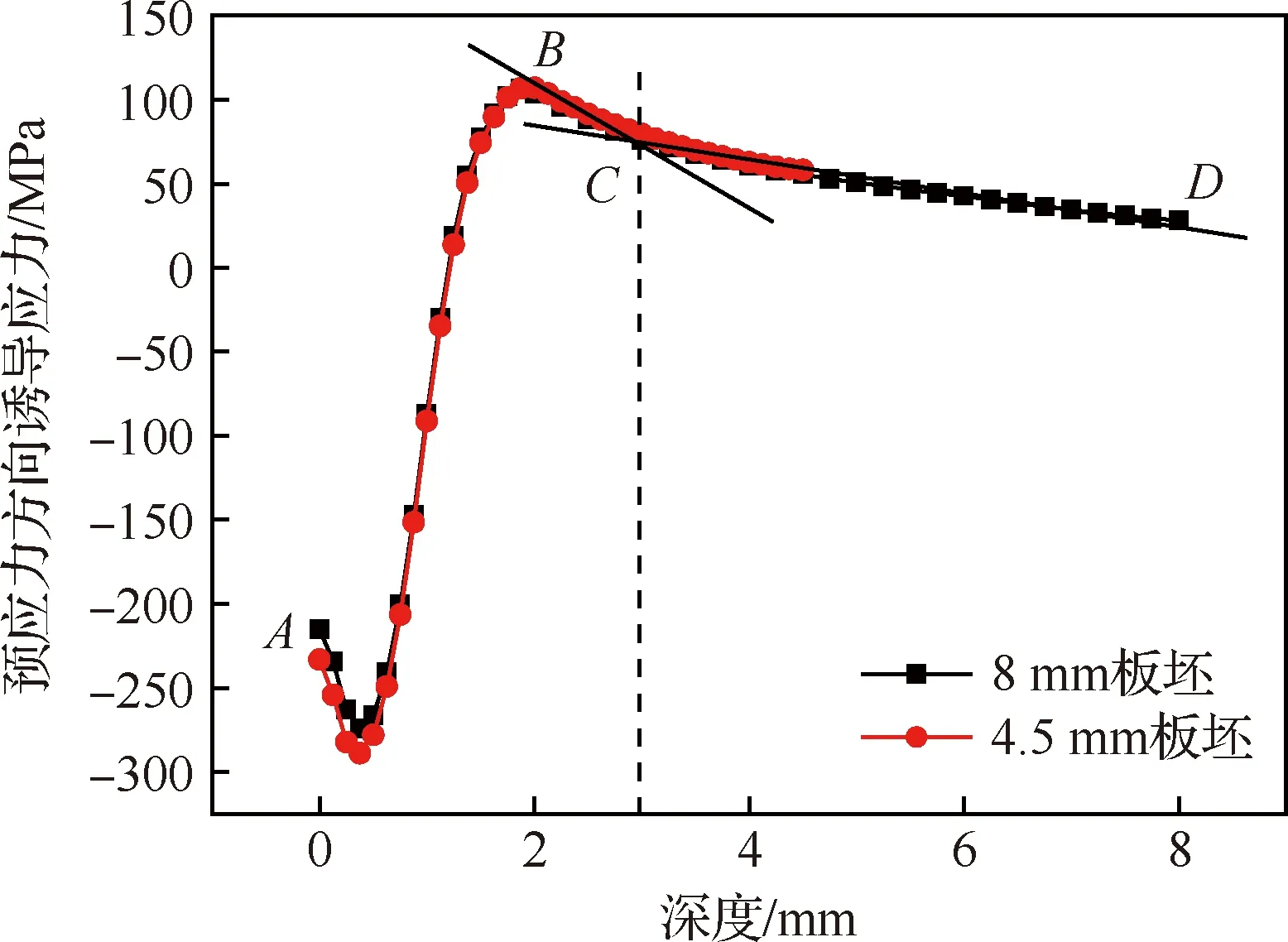
图9 预应力方向多弹丸撞击模型平均诱导应力

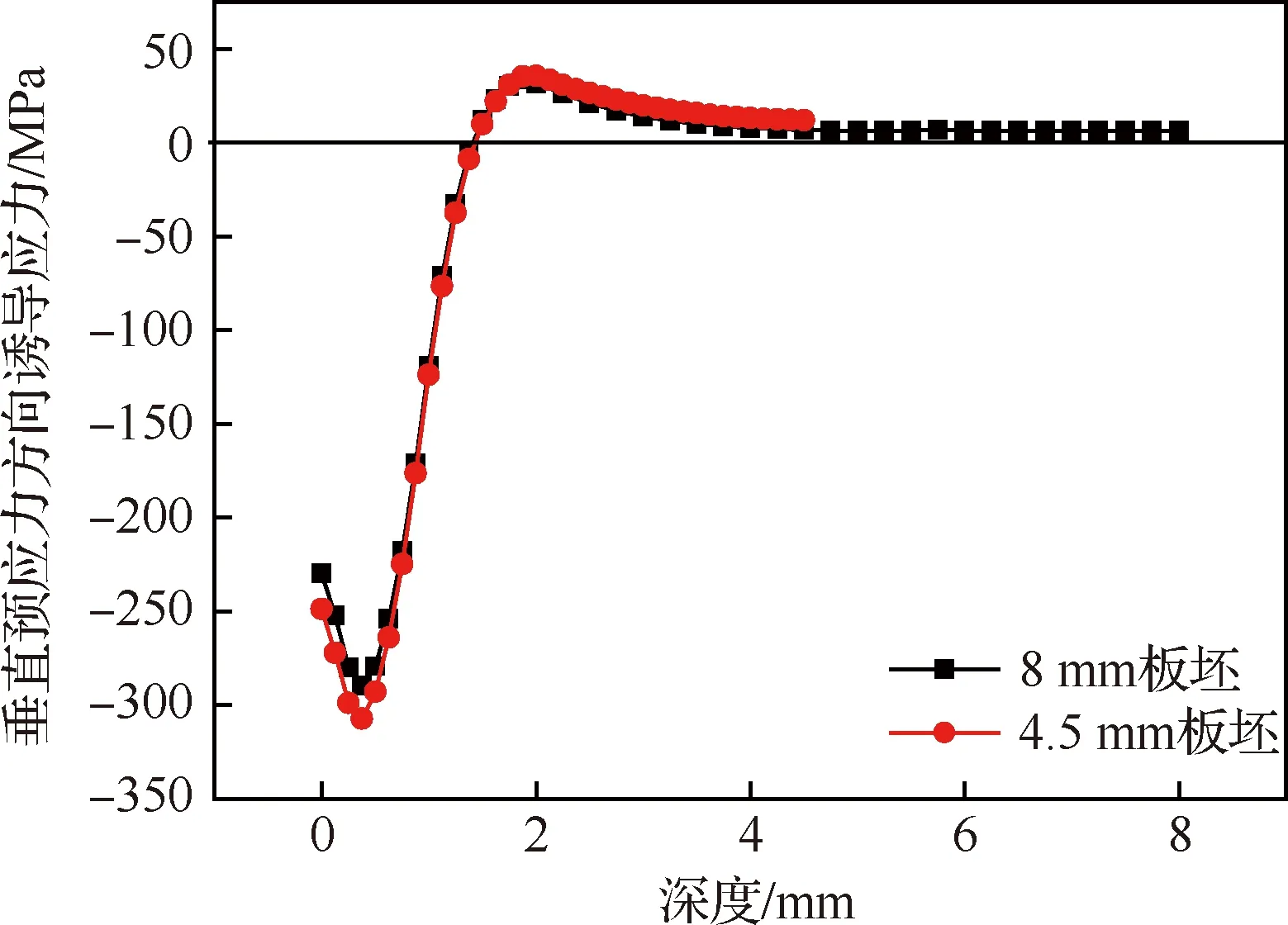
图10 垂直预应力方向多弹丸撞击模型平均诱导应力

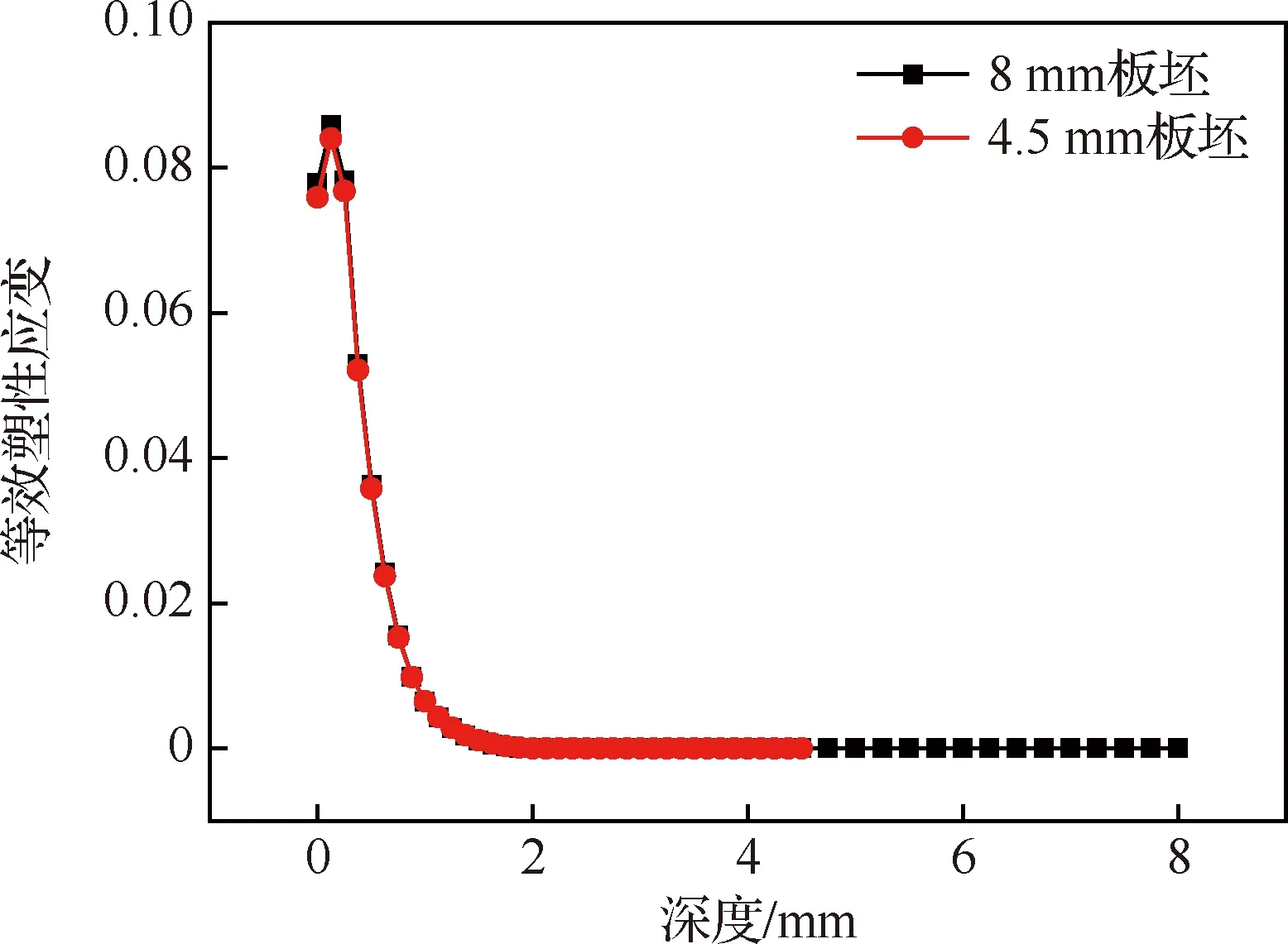
图11 多弹丸撞击模型等效塑性应变

再次，喷丸塑性层平均厚度可以通过后处理模块输出的等效塑性应变(PEEQ)曲线(见图11)获取，塑性层厚度为等效塑性应变大于0的区域的厚度，与图9中AB段对应的厚度相同，也即图9中AB段为塑性层对应的平均诱导应力。

图9中塑性层AB段以外的BD段为弹性层，BD段分BC段和CD段，CD段近乎直线即线性弹性层，BC段为曲线即非线性弹性层简称过渡层。研究表明:CD段诱导应力分布与预弯状态下未喷丸时的同一厚度处应力分布接近；BC段约为AB段的一半厚度，即h1≈2h2，见图7(d)。

因喷丸表面塑性层的存在，应变中性层必然偏离y1处，向截面中心内移[22]。图12为利用表1和表2中的参数得到的受喷材料真实应力-应变曲线，EF段为弹性阶段，FG段为塑性阶段，F点域为弹塑性过渡阶段。分析表明：图9中的塑性层AB段、线性弹性层CD段、过度层BC段的应力状态分别对应图12中的FG段、EF段和F附近区域。

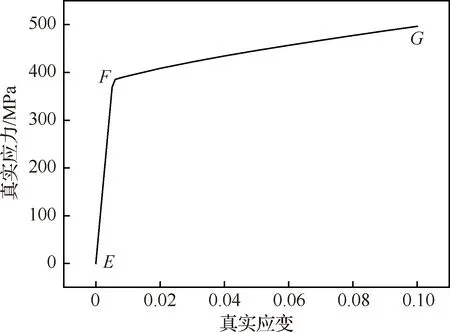
图12 材料真实应力-应变曲线

因此，可以将图7(c)中单筋件截面上的材料分为两种不同弹性模量的材料，一种是塑性层和过渡层，由于处于应变硬化阶段，其弹性模量可以用图12中FG段的斜率代替；另一种为线性弹性层，弹性模量与原材料相同，可以用图12中EF段的斜率代替。两种不同弹性模量材料的组合梁的中性层位置计算公式[23]为

(6)

式中：yn为中性层位置；E1和E2分别为两种异质材料的弹性模量，分别对应图12中EF、FG段的斜率；A1和A2分别为各材料截面积；ym1和ym2分别为两种材料截面形心位置。

由式(6)可以计算出在喷丸结束后图7(c)截面中性层位置y2。

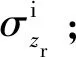
(7)

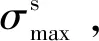
(8)

依据式(7)，得到σs的计算式为

(9)

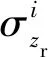
(10)

特别指出，利用式(6)计算的中性层位置是图7(c)中喷丸之后仍在约束状态下的中性层位置，仅为模拟所用；而且反向弯曲是一种假设，不代表实际喷丸成形工艺过程。但是，反向弯曲方法可以方便地赋予诱导应力，有利于带筋整体壁板喷丸变形数值模拟。

最终，将上述诱导应力赋予单筋件壳单元，实现单筋件喷丸成形数值模拟。

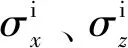
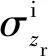
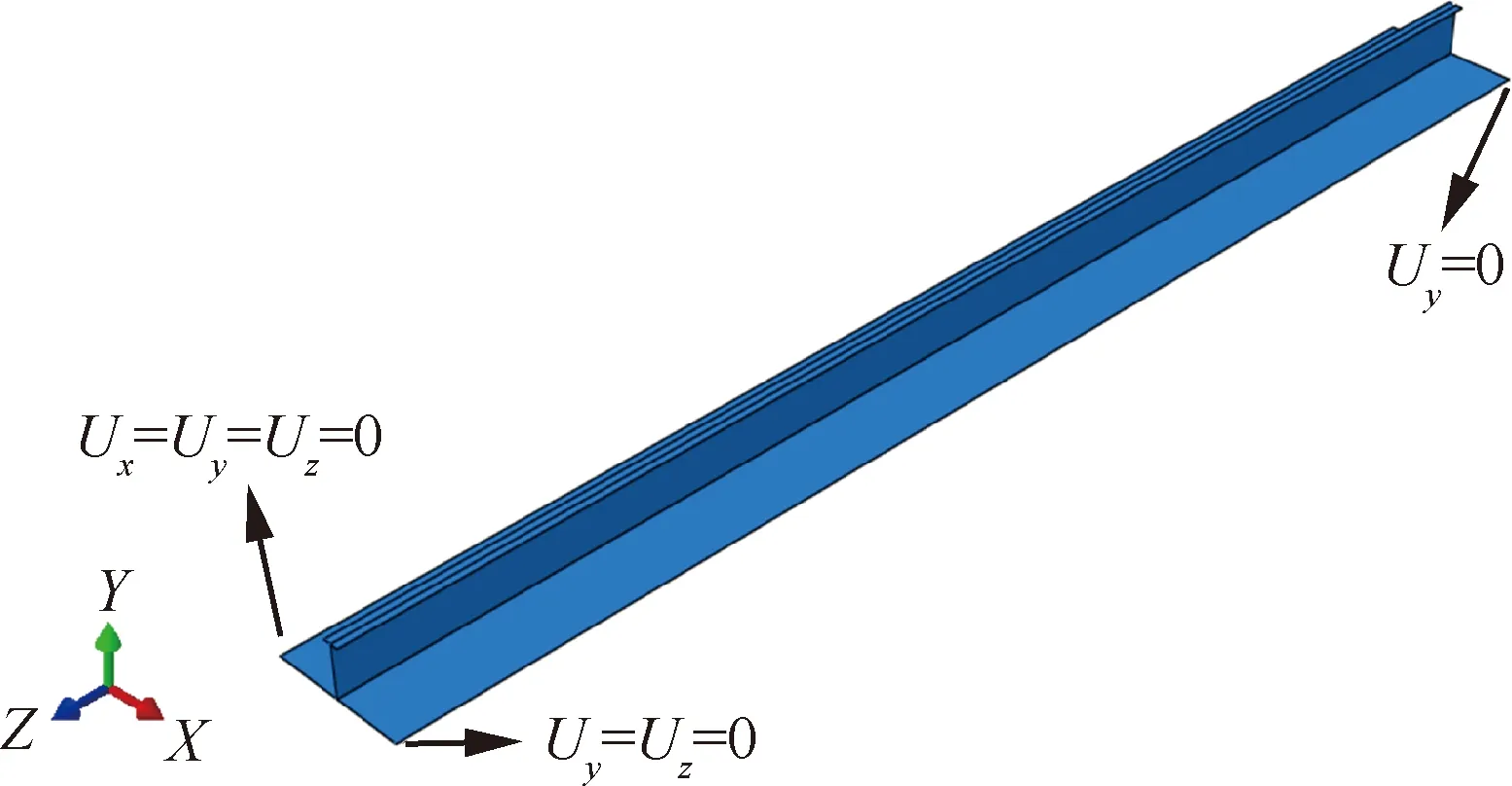
图13 单筋件壳单元模型

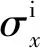
图14 单筋件喷丸成形模拟变形形状

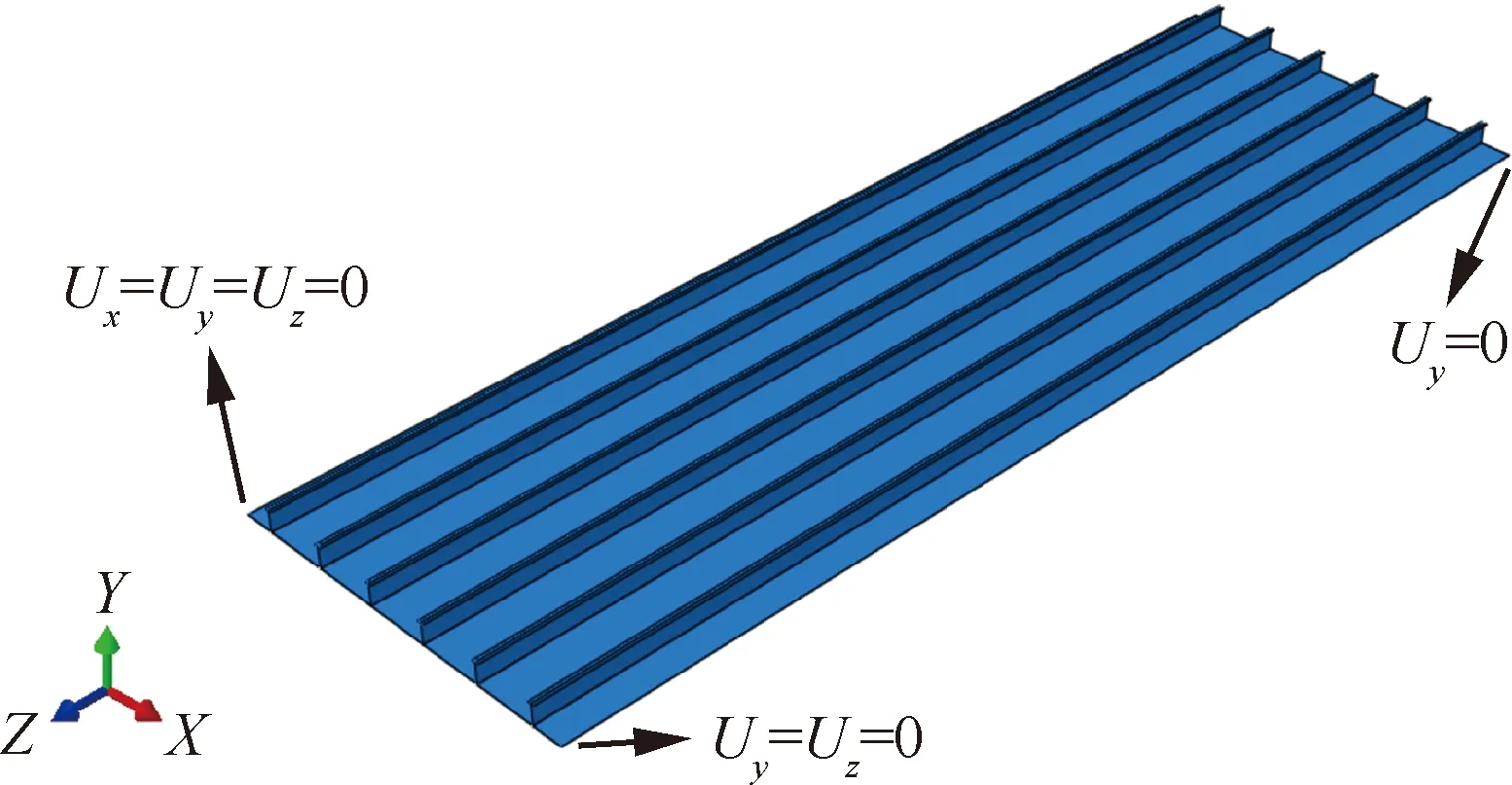
图15 带筋整体壁板壳单元模型

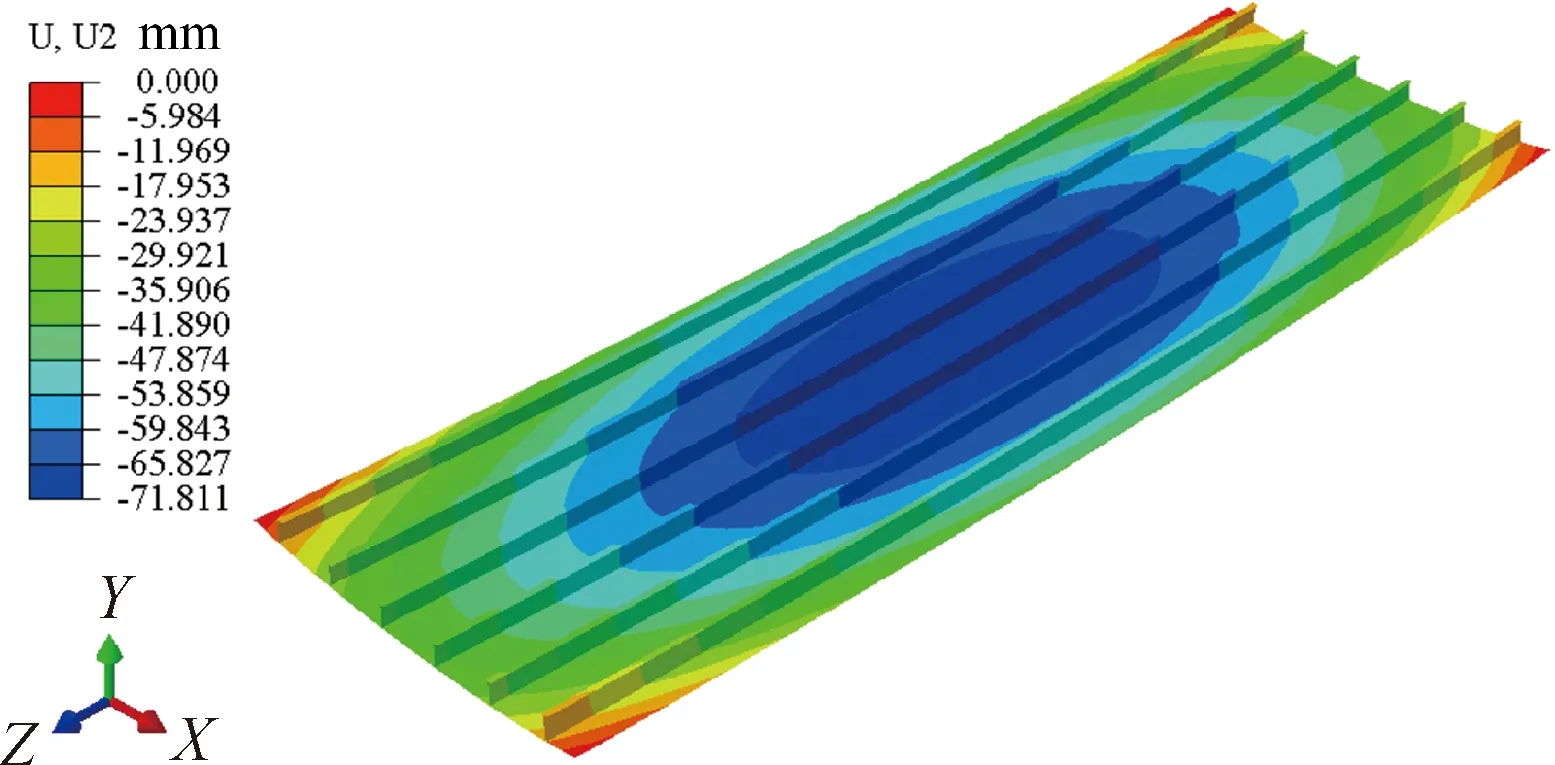
图16 带筋整体壁板喷丸成形模拟变形形状

2.2 试验验证

采用四点弯曲方式，预应力装夹单筋件见图17。其他试验条件同第1节平板件试验条件。

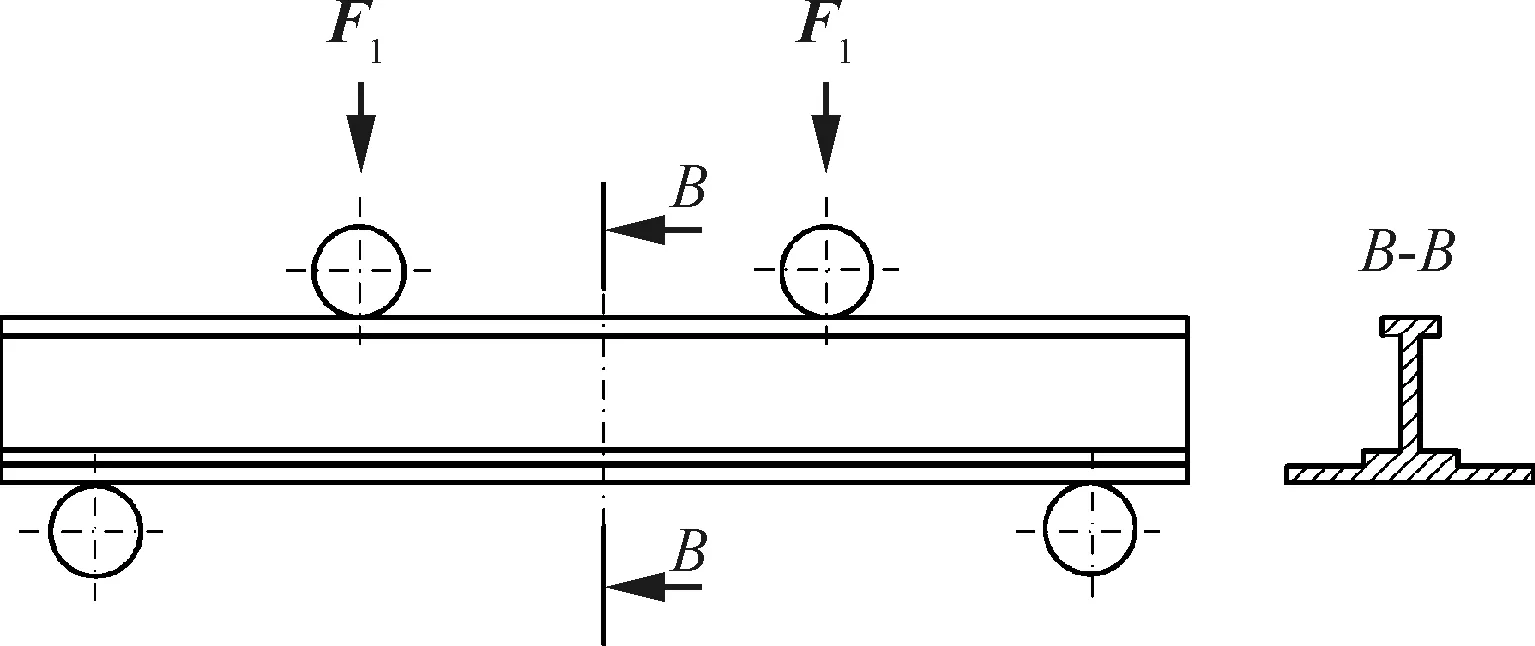
图17 单筋件预应力装夹

依据2.1节单筋件中性层高度y1及表2中2024-T351材料屈服强度369 MPa，得出单筋件蒙皮外表面弹性预应力σ的最大值为87 MPa。在预应力加载过程中，通过预先粘贴在单筋件表面的应变片实时检测预应力值。单筋件的数据测量点选择3个，位于力F1(见图17)的两个施力点之间，分别为筋顶表面中心线中心点及向两端相距100 mm处的两点,见图18。用弧高仪分别测量喷丸前和喷丸后3个测量点处的弧高值，将3个测量值的平均值作为试验件的弧高值。

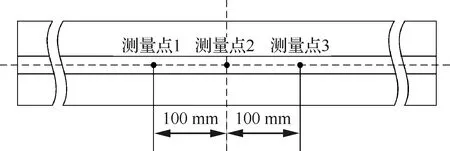
图18 单筋件数据测点位置

根据试验参数并结合式(2)～式(4)获得相应模拟参数见表3。对3件单筋件分别进行预应力喷丸成形试验和反弯曲应力场法数值模拟，试验及相应模拟结果即弯曲半径值见表4，喷丸后的试验件实物照片见图19。

表4数据显示，单筋件预应力喷丸成形数值模拟结果与试验结果相对误差仅2.1%～5.8%。表明该反弯曲应力场法数值模拟方法比较科学合理，适用于单筋件预应力喷丸成形较高精度的数值模拟。

鉴于典型单筋件在带筋整体壁板上的位置区域、种类数量、结构壁厚、预应力及工艺参数的可选择性与可设计性，以及典型单筋件预应力喷丸成形的难易程度、工艺数据和变形规律是带筋整体壁板预应力喷丸成形工艺分析、方案及参数确定的基本依据，因此反弯曲应力场法数值模拟方法也适用于带筋整体壁板预应力喷丸成形较高精度的数值模拟。

表3 喷丸试验及模拟参数

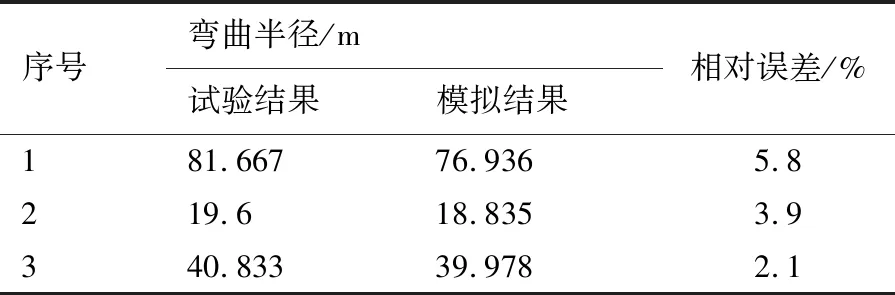
表4 喷丸试验及模拟弯曲半径

图19 喷丸成形单筋件实物

3 带筋整体壁板预应力喷丸成形预测模型

与BP神经网络相比，RBF神经网络具有结构简单、收敛速度快，能够逼近任意非线性函数且不会陷入局部最优的特点，因此采用RBF神经网络建立弯曲半径与预应力喷丸成形工艺参数之间的预测模型。

3.1 RBF神经网络

RBF神经网络由输入层、隐含层和输出层构成 见图20，图中，隐含层第i个节点的输出为

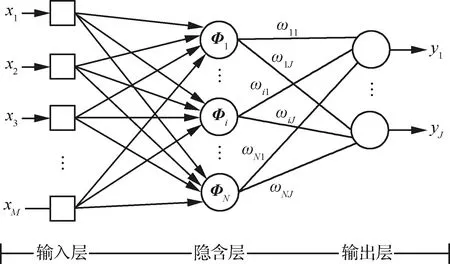
图20 RBF神经网络结构

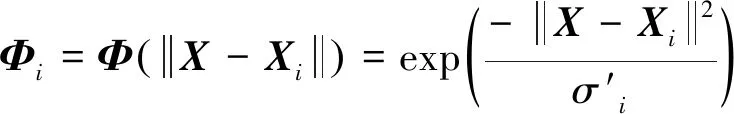
(11)

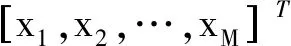
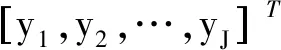
(12)

式中：ωi为隐含层到输出层的连接权值。

在MATLAB软件中，可以通过调用newrbe函数生成一个零误差的RBF神经网络。其调用格式为

net=newrbe(X,Y,spread)

(13)

式中：spread为径向基函数的扩散速度，缺省时为1。

通常，依据由输入向量和输出向量组成的训练样本向量，以及测试样本向量，经过训练、测试并确定最终RBF神经网络模型。

3.2 训练样本向量

针对单筋件预应力喷丸成形，按照正交表L16(45)规划的喷丸工艺参数组合方案，其中正交因素选取喷丸气压、弹丸流量、进给速度及预应力等4项，各因素选取4个水平，见表5。喷丸工艺参数组合方案见表6，依此通过式(2)～式(4)获得模拟参数值，然后采用反弯曲应力场法进行单筋件喷丸成形模拟，模拟结果见表6，其中的工艺参数和模拟结果一起组成训练样本向量。

3.3 测试样本向量

与训练样本向量的获取过程类似，针对单筋件预应力喷丸成形，按照均匀表U4(44)规划的喷丸工艺参数组合方案，其中因素及水平选取同表5。喷丸工艺参数组合方案及模拟结果见表7，其中的工艺参数和模拟结果一起组成测试样本向量。

表5 正交因素水平表

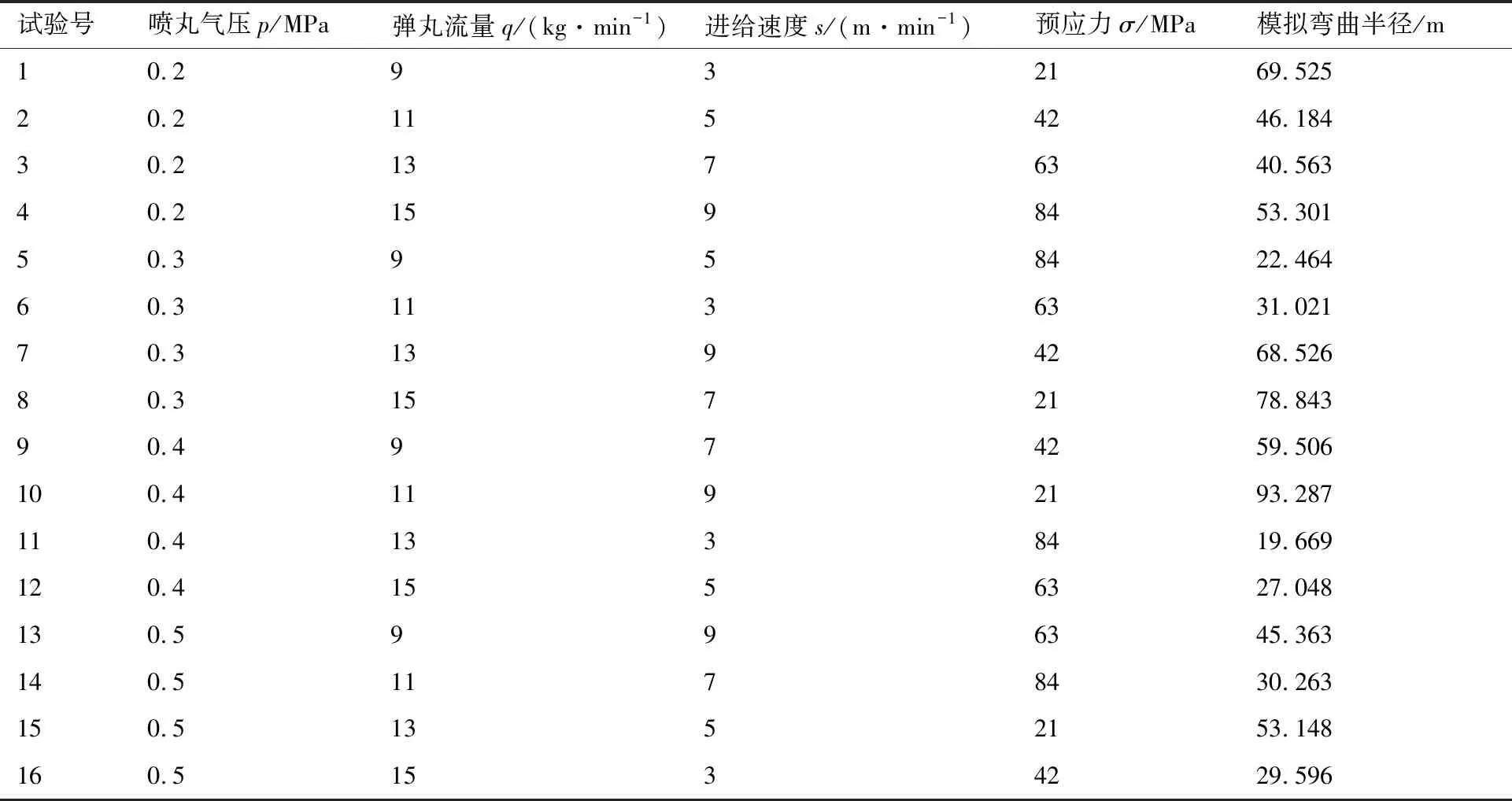
表6 正交方案/训练样本向量

表7 均匀方案/测试样本向量及预测结果

3.4 RBF神经网络预测模型建立及测试

依据训练样本向量、调用newrbe函数、选取spread初始值(>0)，训练并建立用于测试的神经网络模型；以该模型泛化能力最大化为标的，依据测试样本向量，优化并最终确定spread值，由此RBF神经网络预测模型建立。

综合分析表明，当spread取值21时，一方面预测误差的平均值和最大值均最小(见图21)，模型预测精度最高、泛化能力最佳；二方面各测试样本点具体预测误差见表7，最大误差为7%，平均误差为5.1%。通常，5%左右的平均误差已经能够基本满足单筋件和带筋整体壁板预应力喷丸变形的工程预测需要。由于测试样本向量独立于训练样本向量，因此所建立的RBF神经网络预测模型也适用于其他样本向量，即该模型具有一定的普遍适用性。

与数值模拟相比，预应力喷丸成形RBF神经网络预测模型一方面在一定程度上无需反复建模求解，应用更加简捷、效率更高、成本更低；另一方面，通过重构可以由变形反向预测预应力喷丸工艺参数。

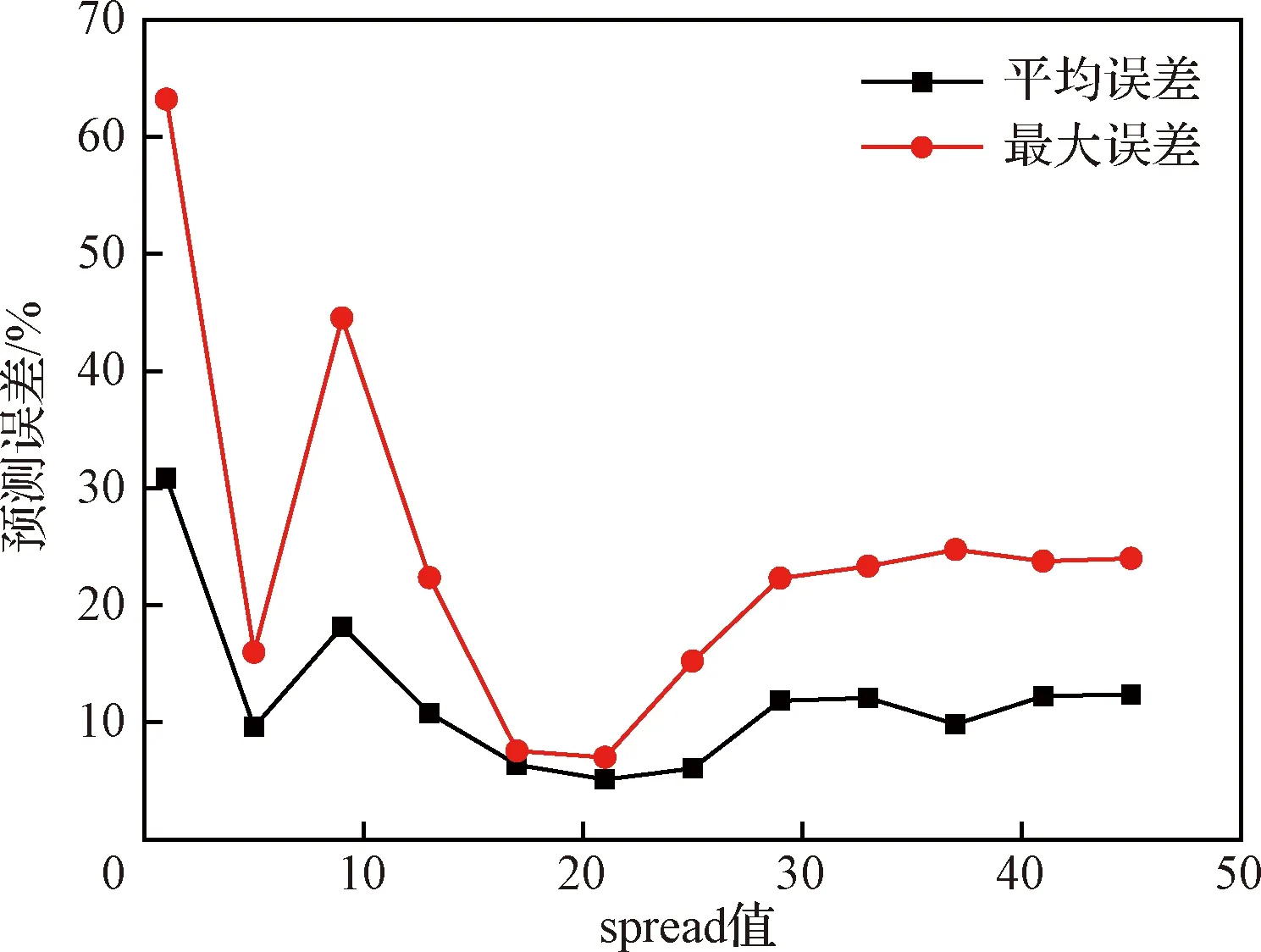
图21 预测误差随spread值变化的曲线

4 结 论

1) 基于响应面函数的多弹丸撞击模型可以获得诱导应力，用于实现应力场法对自由状态和预应力状态的整体壁板以及自由状态的带筋整体壁板喷丸成形数值模拟，是带筋整体壁板预应力喷丸成形应力场法数值模拟的必要条件。

2) 借助诱导应力，运用基于应变中性层内移的反弯曲应力场法有限元模型，能够实现带筋整体壁板预应力喷丸成形的较高精度数值模拟，有助于结构效率、减重效益、使用性能俱佳的带筋整体壁板在航空航天器上的推广应用。

3) 带筋整体壁板预应力喷丸成形RBF神经网络预测模型，在一定程度上为整体壁板和带筋整体壁板预应力喷丸成形技术研究和实际应用，提供了一种更为便捷、高效、经济的途径。此外，应用RBF神经网络，可以由变形预测预应力喷丸工艺参数。