AR模型中AO类异常值探测及其在GPS卫星钟差预报中的应用

韩松辉，张国超，张 宁，朱建青

1. 信息工程大学基础部，河南 郑州 450001； 2. 中国人民解放军78092部队，四川 成都 610000； 3. 苏州科技大学理学院，江苏 苏州 215009

时间序列分析是处理测绘导航数据的常用技术之一，比如使用时间序列模型对卫星钟差数据进行处理就具有明显的优势[1-2]。但是，卫星钟差的历史观测序列中可能包含AO类异常值(只对出现异常值历元的观测值产生影响，不影响其他历元的观测值)[3-4]，这严重影响了时间序列模型识别和参数估计的精度。目前已有一些学者对时间序列中异常值的探测问题进行了研究，并提出了许多解决方法，如中位数法[5]、抗差估计法[3,6]、Allan方差法[7-8]和抗差自适应滤波法[9]等。但已有的方法均存在一定的不足之处，如对异常值的定位存在偏差，无法有效地对异常扰动进行估计等[10]。异常值探测是时间序列分析中的一个重要环节[11-15]，如何基于时间序列模型，对序列中的AO类异常值进行探测正逐渐被学者所关注。文献[16]使用时间序列中的AR模型、Bayes统计理论对序列中的异常值进行探测，进而修正了相应的AR模型。文献[17—18]采用平稳时间序列的χ2检测法检测卫星钟运行中的异常情况。文献[19]利用Bayes理论在AR模型中引入识别变量，通过比较这些识别变量的后验概率值与事先给定的阈值来进行异常值探测。上述基于时间序列的算法对于序列中的异常值探测均有一定的参考意义，但是以上几种算法有的未对异常扰动进行估计，有的需要经过复杂的抽样过程，有的需要计算后验概率。

时间序列中异常值探测的相关计算比较复杂，可以采用基于极大似然函数的EM算法(expectation maximization algorithm)[20]进行处理。极大似然函数包含了每一个观测值的信息，使用极大似然函数对观测序列中的异常值进行探测是很好的选择。EM算法已经被广泛应用于处理缺损数据、截尾数据、成群数据、带有讨厌参数的数据以及对异常扰动视同缺失进行再补充的不完全数据等[21-26]。EM算法是一种简单稳定的迭代算法，每一次迭代都能保证似然函数值增加，并最终收敛到一个局部极大值。已经有多位学者使用EM算法对时间序列问题进行了研究，部分成果已经成功用于解决实际问题，比如，EM算法应用于线性时间序列参数估计与预测、非线性时间序列参数估计、整值时间序列参数估计以及回归混合模型参数估计等[27-31]。目前，也有学者讨论了基于EM算法的异常扰动处理问题，比如，t型估计中异常扰动的处理问题[32-33]，非高斯噪声线性回归模型中异常扰动的处理问题[34]，均值漂移模型和方差膨胀模型中异常扰动的处理问题[35]。但是，目前极少有学者讨论基于EM算法的时间序列异常值探测问题。文献[31]提出了采用EM算法估计MPT(1)模型参数的算法，虽然文中分析了该算法对异常值的抗干扰能力，但是并没有进一步提出异常值的探测方法。

本文将EM算法应用于AR模型观测序列AO类异常值的探测与修复之中。首先，基于AR模型，给出引入识别变量的AO类异常值探测模型。然后，利用EM算法推导AR模型中AO类异常值的定位与异常扰动估值的迭代公式，提出一种AR模型中AO类异常值探测算法。该算法通过简单迭代计算出AR模型系数、异常值的位置和异常扰动的估值。最后，为了验证本文算法的有效性，分别给出仿真算例和实测GPS卫星钟差算例，并分别对单个AO类异常值和成片AO类异常值进行探测。分析发现本文算法对单个AO类异常值和成片AO类异常值均可精确探测，并且在探测成片AO类异常值时，未出现掩盖和淹没现象。

1 异常值探测模型和EM算法

1.1 异常值探测模型

设时间序列数据{yt}符合AR(p)模型，则有

(1)

基于识别变量标记异常值方法，可以建立基于AR模型的AO类异常值探测模型[10,19]

(2)

式中，{xt}为观测得到的可能包含AO类异常值的时间序列；{yt}为无法观测的正常序列；δt为AO类异常值的识别变量，并且δt服从两点分布，取值为0或1，如果δt=1，则xt包含AO类异常值，相应AO类异常值的异常扰动大小为wt，如果δt=0，则xt不包含AO类异常值。在上述构造的AO类异常值探测模型中，增加了探测异常值的参数δt、wt，基于此模型探测异常值时，如何正确估计模型中的未知参数是首要问题。当观测数据含有异常值时，应利用数据中包含的一切有用信息来消除异常值的影响。极大似然函数包含了每一个观测值所提供的信息，可采用极大似然函数进行异常值探测。但是，由于极大似然函数比较复杂，此时面临模型系数如何计算、异常值位置如何判定、异常值扰动如何估计等问题。为此，本文引入求解极大似然函数方程的EM算法来解决相关计算问题，进而确定模型参数、异常值位置和异常扰动的大小，从而准确拟合出时间序列模型，并获得精确的异常值探测结果。

1.2 EM算法

EM算法也称为期望最大化算法，是一种求参数的极大似然估计的方法，可以从非完整数据集中对参数进行极大似然估计[20]。在统计学中，EM算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量。本文构造的异常值探测模型(2)中，增加的异常值识别变量δt可看成无法观测的隐藏变量，因此基于AR(p)的异常值探测模型(2)可以采用EM算法进行求解。

令

首先初始化分布参数θ，则由θi计算θi+1的过程由下面两步组成：

第1步：利用概率模型参数的现有估计值，计算隐藏变量的期望，即对给定的θi，利用对数似然函数lnL计算Q(θ|θi)=Eδt[lnL|X,θi]；

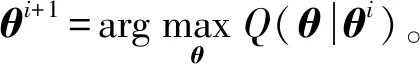
按以上两步循环迭代，直至收敛，进而获得参数θ的估计值。在宽松的初始条件下，由EM算法产生的迭代序列{θi}将收敛到似然函数的极值点[36]。

2 基于EM算法的AO类异常值探测方法

由模型(2)可知，xt的概率密度函数为

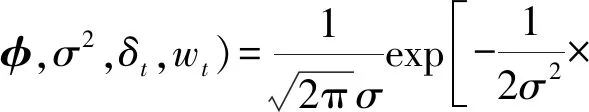
(3)

似然函数为

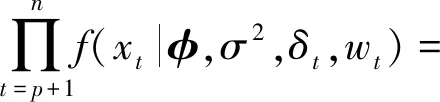
(4)

其对数似然函数为

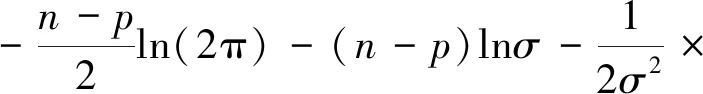
(5)

异常值识别变量δt是无法观测的隐藏变量，可采用EM算法进行求解。

2.1 计算隐藏变量的期望

令zt=xt-φ1yt-1-…-φpyt-p，则

Q(θ|θi)=Eδt[lnL|X,θi]=

(6)

式中

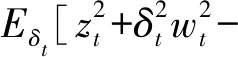
2δtwtzt|θi)]

(7)

已知δt服从0～1分布，令

(8)

此时

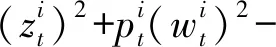
(9)

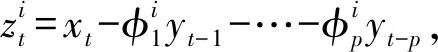
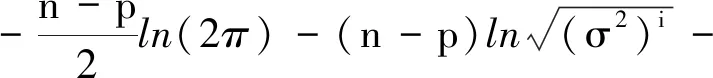
(10)

2.2 模型参数的最大似然估计

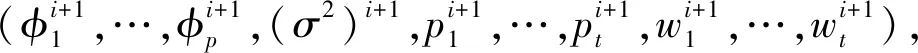
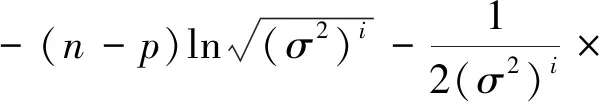
(11)

达到最大。为方便符号表示，在下面的推导过程中省略Q(δ)中的上标i。将Q(δ)分别关于φ1、φ2、…、φp,求导并令其等于零，可得

(12)

将上式整理成矩阵形式为

(13)

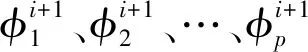
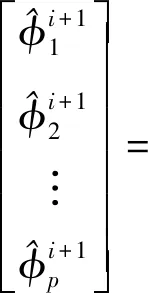
(14)

同理，将Q(δ)分别关于wt、σ2求导并令其等于零，可得

(15)

(16)

该算法不但可以消除异常值的影响而且可以同时得到准确的AR模型。在以上算法中，模型系数、异常值识别变量和异常扰动大小表达式均为严格推导所得的结果，具有理论上的严密性。算法既利用了原始观测数据，又同步使用了修正异常扰动后的观测数据对异常值进行探测，使得计算结果既不偏离原始数据又可消除异常值的影响。另外，算法的所有估计结果均是在一个迭代循环过程中获得的，估计值之间具有较好的相容性，不会额外引入不同迭代过程之间的计算误差。

2.3 AO类异常值探测流程

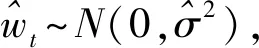
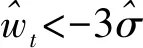
(17)

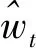
重复第1步(计算隐藏变量的期望)与第2步(模型参数的最大似然估计)，迭代收敛后即可得参数最终解。具体的程序流程如图1所示。

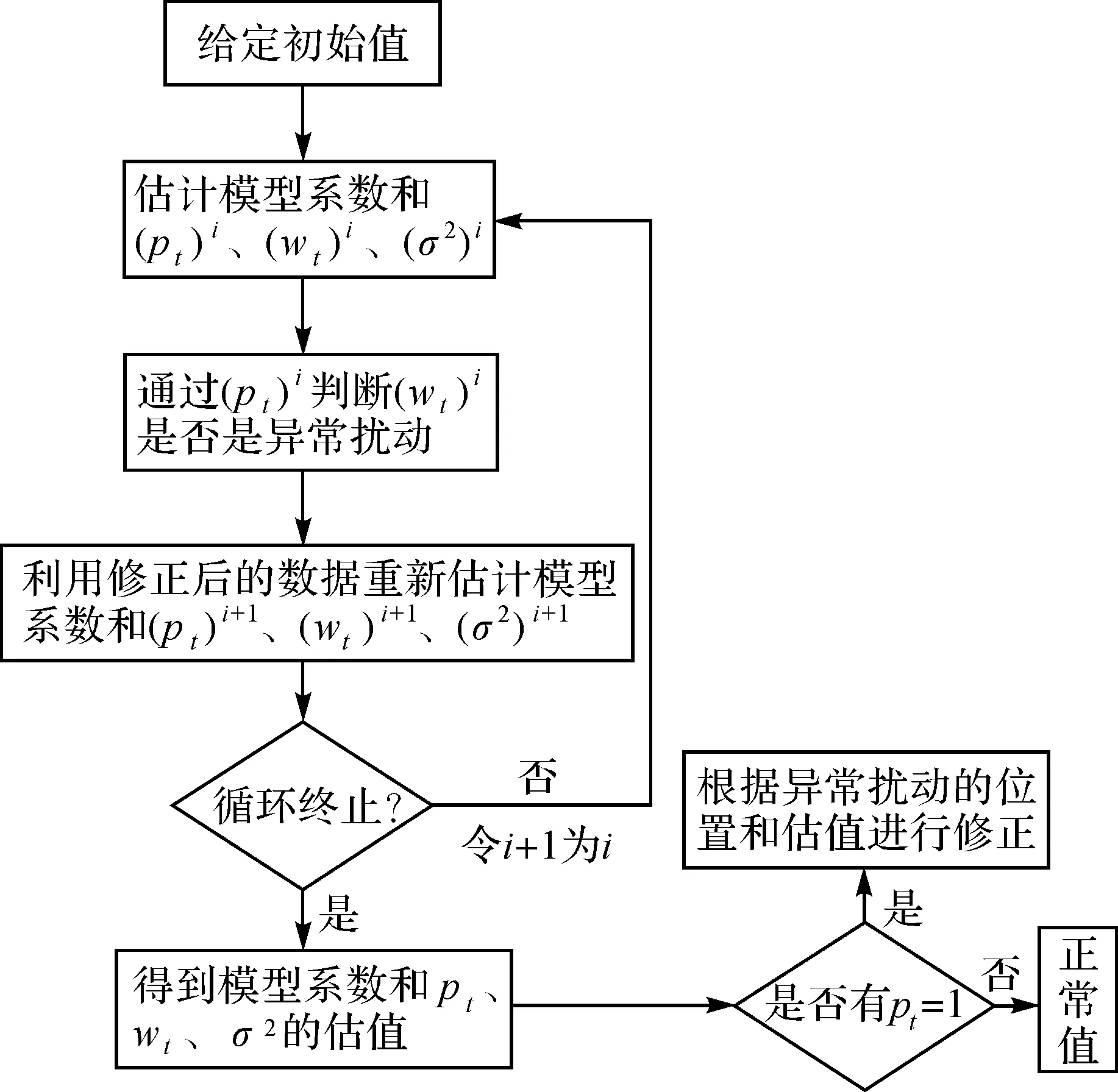
图1 基于EM算法的AR模型异常值探测与估计流程Fig.1 Flowchart of outliers detection and estimation in AR model based on EM algorithm

3 算例与分析

为验证本文方法的有效性，给出一个仿真算例和一个卫星钟差预报算例。

3.1 仿真算例

使用AR(2)模型

生成50个模拟观测值，并在第20个和第30个观测值分别添加数值为10和7的AO类异常扰动。使用本文算法对异常值进行探测，并采用常用的3σ原则，所得模型识别变量pt与异常扰动估计wt的结果如图2、图3所示。其中，图3中的星号是真实的AO类异常扰动大小。在后续计算分析中，均采用星号表示真实异常扰动的大小。

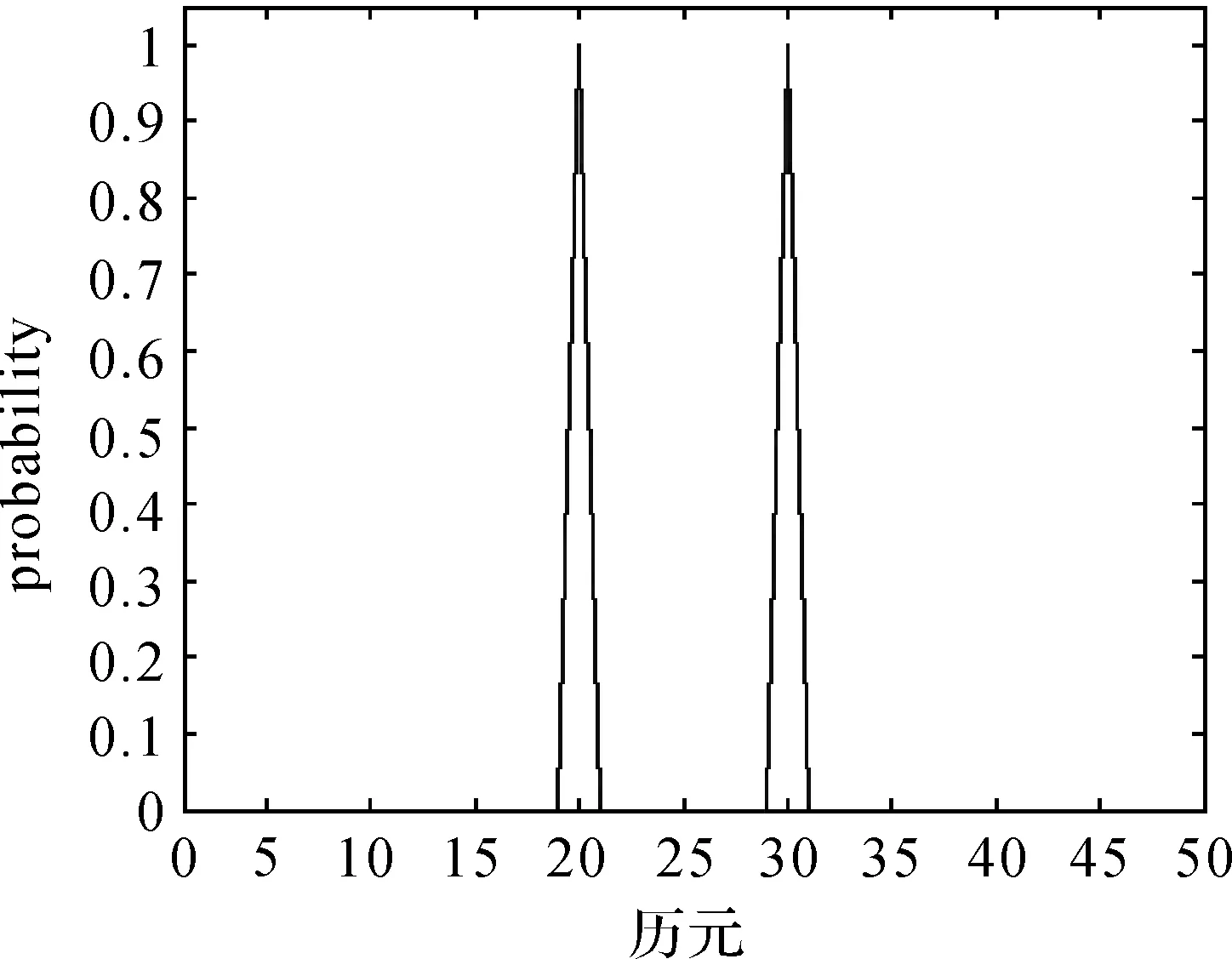
图2 仿真数据中单个异常扰动的pt结果Fig.2 ptof single outlier in simulation data

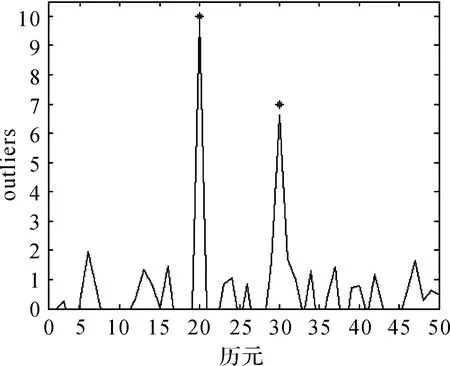
图3 仿真数据中单个异常扰动的wt结果Fig.3 wt of single outlier in simulation data

分析发现，本文方法可以精确确定AO类异常值的位置，并准确估计异常扰动的大小，所得异常扰动的估计值分别为9.89和6.63。

为检验本文方法对成片AO类异常值的探测效果，在第20—24个观测值上分别加上大小为10的AO类异常扰动，并使用本文提出的算法进行异常值探测，其中pt和wt的计算结果如图4、图5所示。

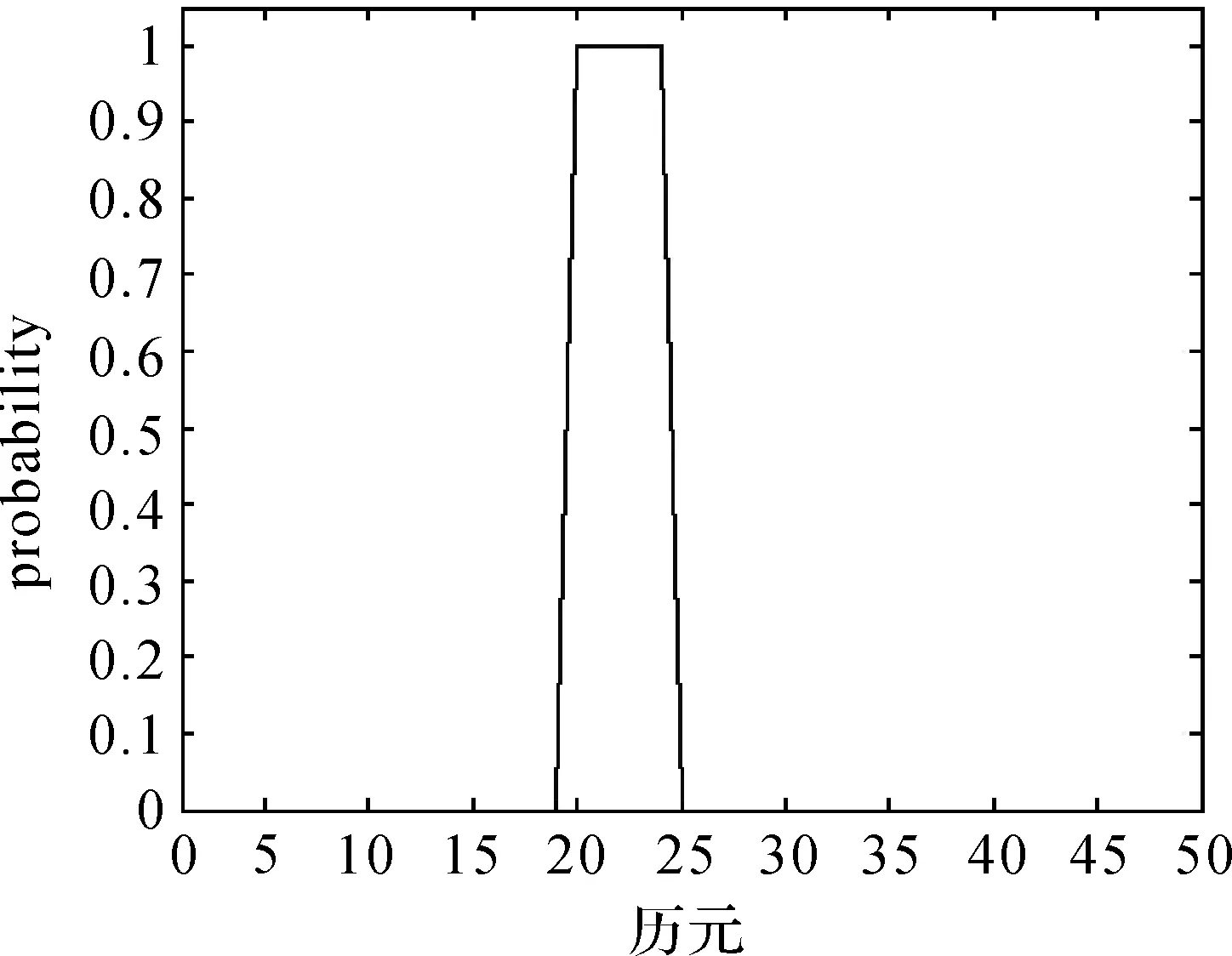
图4 仿真数据中成片异常扰动的pt结果Fig.4 pt of patches of outliers in simulation data

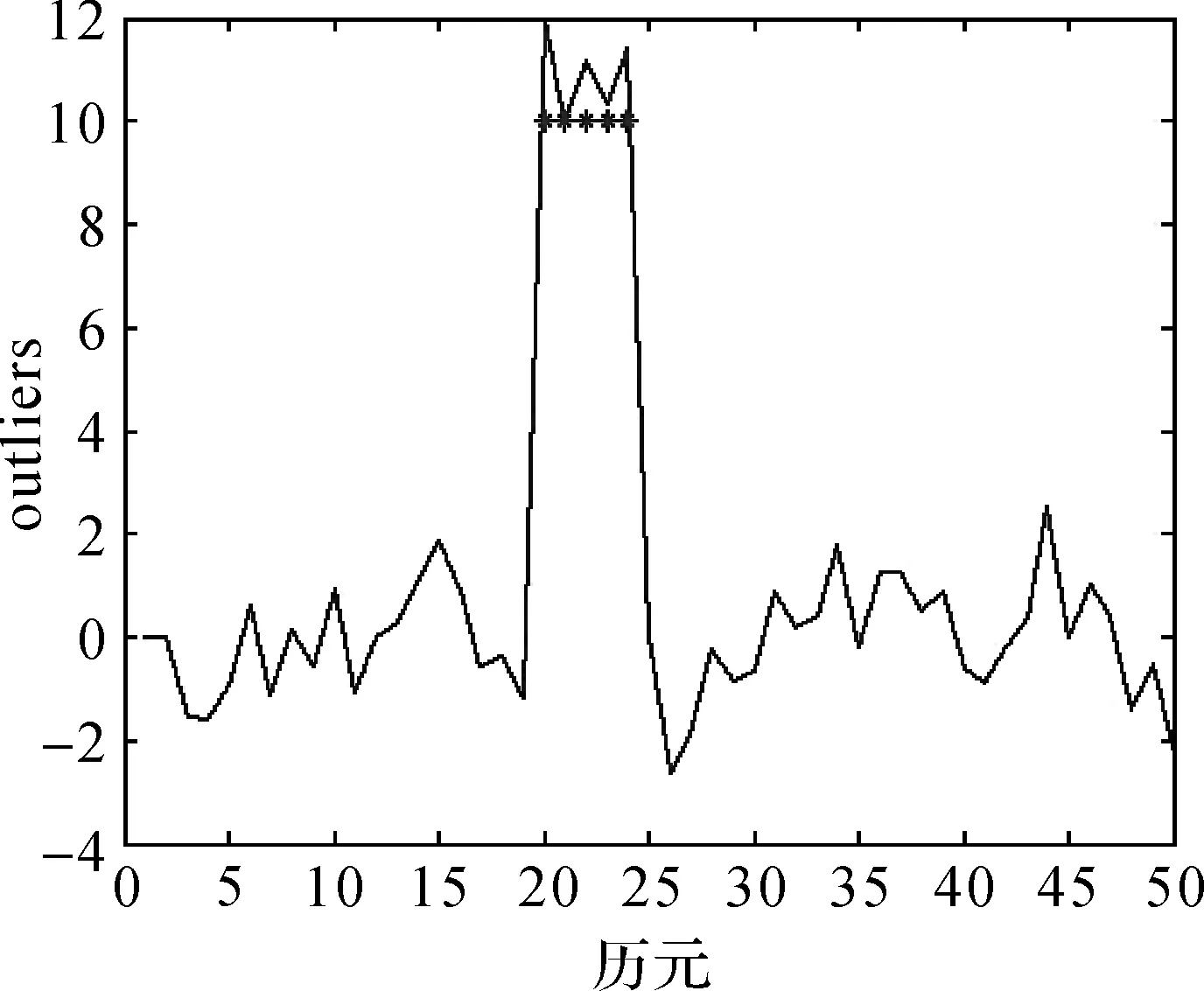
图5 仿真数据中成片异常扰动的wt结果Fig.5 wt of patches of outliers in simulation data

分析发现，本文方法对成片AO类异常值的定位非常准确，对相应异常扰动大小的估计精度较好，所得异常扰动的估计分别为：11.96、9.95、11.19、10.34、11.40。由计算结果可以看出，本文方法可以对成片AO类异常值进行准确探测，并且没有出现掩盖和淹没现象。

为了对异常值的数量比例、探测成功率、估计精度等进行统计分析，首先尽可能多地增加成片异常值中AO类异常值(大小为10)的个数。发现在总观测个数是50的情况下，该算法可以准确探测出第14—32位置上的19个AO类异常值，并且异常扰动大小的估计精度也较好。其估计结果分别为：11.09、12.17、11.51、9.91、9.66、8.74、11.62、9.82、11.14、10.33、11.39、10.03、9.03、8.10、9.25、8.88、9.02、10.59、10.29。

其次，分析第20—24个观测值包含的AO类异常值大小不同的情况。依次加上异常扰动大小为3到9的AO类异常扰动。计算发现，除异常扰动大小为3的情况外，其余情况均可准确探测出异常值位置，并可较准确地估计异常扰动大小，其异常扰动大小的估计值如表1所示。

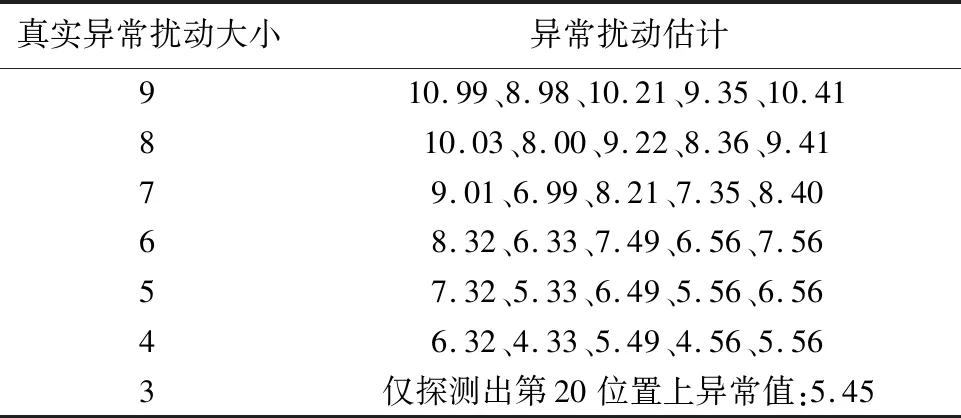
表1 不同大小异常值的估计值

由表1可以发现，当异常扰动越大时异常扰动大小的估计精度越高。当异常扰动大小为3时之所以无法准确探测异常值位置，是因为此时的异常扰动大小与正常的观测值非常接近(不含异常值时，观测序列的最大观测值为2.58)，此时本算法探测效果不好。

接下来，分别在第20个观测值、第20—21个观测值、第20—22个观测值、第20—23个观测值、第20—24个观测值加上大小为10的异常值，在每次计算时均生成50个新的模拟观测值并分别计算10 000次，其成功探测异常值位置的计算结果如表2所示。

表2 采用3σ原则时异常值位置探测的成功率

Tab.2 The frequency which the location of outliers was correctly detected when 3σwas used

异常值位置2020—2120—2220—2320—24成功率/(%)89.1284.1077.4469.5361.84

由表2可以看出，随着成片AO类异常值中异常值个数的增加，异常值探测成功率是逐渐降低的。分析异常值探测失败的情况，发现3σ作为阈值偏小，有些不是异常值的情况被误判为异常值。因此采用4σ原则，在每次计算时均生成50个新的模拟观测值并分别计算10 000次，其成功探测异常值位置的计算结果如表3所示。

表3 采用4σ原则时异常值位置探测的成功率

Tab.3 The frequency which the location of outliers was correctly detected when 4σwas used

异常值位置2020—2120—2220—2320—24成功率/(%)99.9795.1191.3286.4782.12

由表2和表3可以看出，异常值的探测效果受σ倍数k的影响，虽然采用3σ作为阈值也可以得到较好的异常值探测效果，但是采用4σ原则时异常值探测成功率明显上升。如何找到最恰当阈值是一个需要继续研究的问题。对此，文献[37]认为：在时间序列异常值的探测过程中，阈值过大或过小均不利于异常值探测，在实际中可以设定几个不同的阈值以便发现数据的结构变化。

3.2 实测算例

随着卫星导航定位技术的发展，高精度的钟差预报技术显得至关重要。一般的，对卫星钟差进行预报需要建立准确的钟差预报模型。时间序列模型可以充分考虑到卫星钟差的趋势性、周期性和随机性等特点，因此，使用时间序列模型对卫星钟差数据进行处理具有明显的优势。由于传播路径和观测环境的影响，钟差的历史观测序列可能包含异常值，这严重影响了卫星钟差预报的精度。

在IGS官网发布的GPS卫星精密钟差数据中提取为期1 d的G16卫星的钟差数据(单位为秒)，时间为2016年01月01日，数据采样间隔为5 min，共包括288个历元。经过两次差分后序列变为不含趋势项的平稳序列，其自相关函数和偏自相关函数的计算结果分别如图6和图7所示。

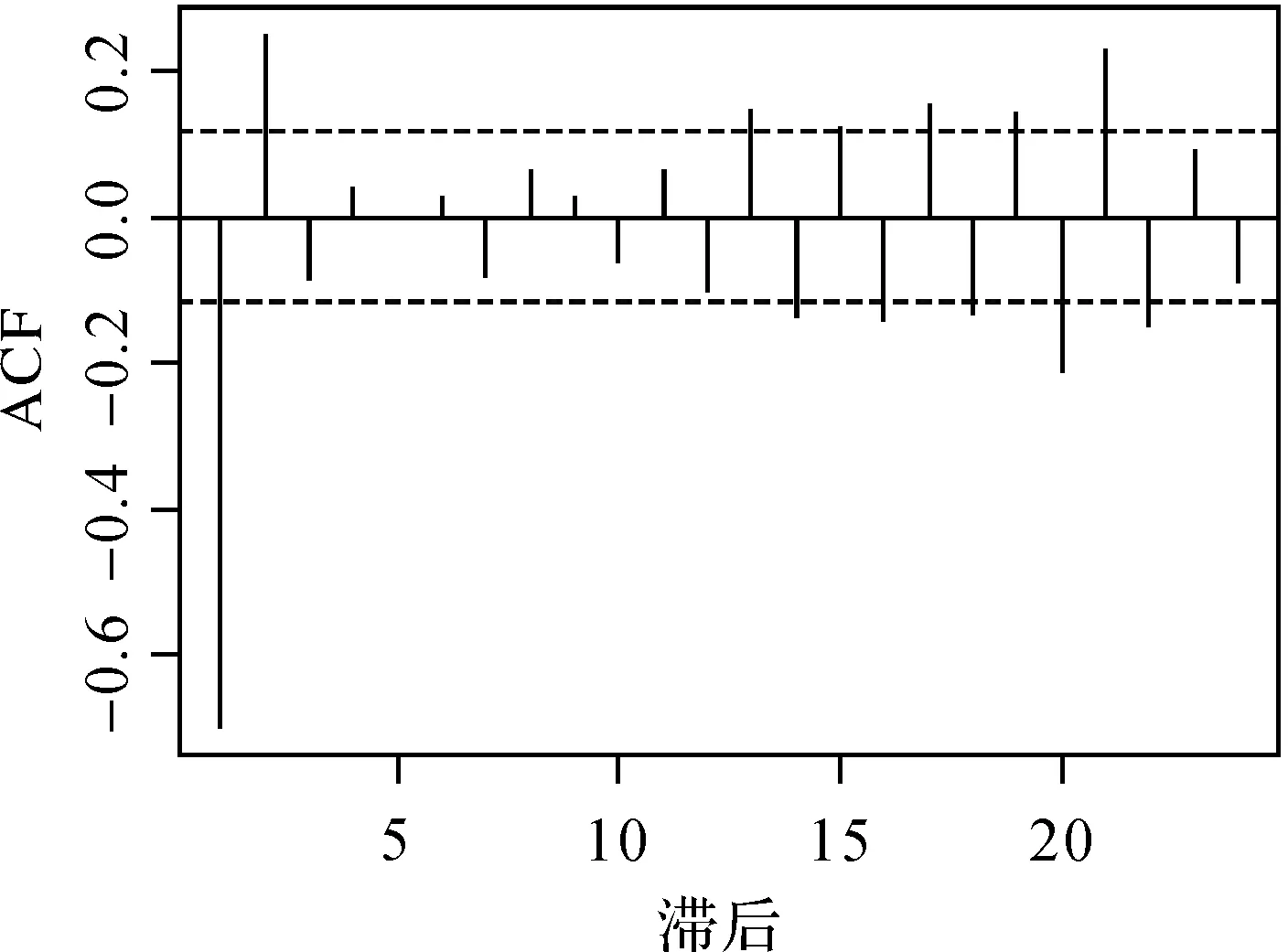
图6 二次差分钟差数据的自相关函数图Fig.6 Sample ACF of two differences clock errors data

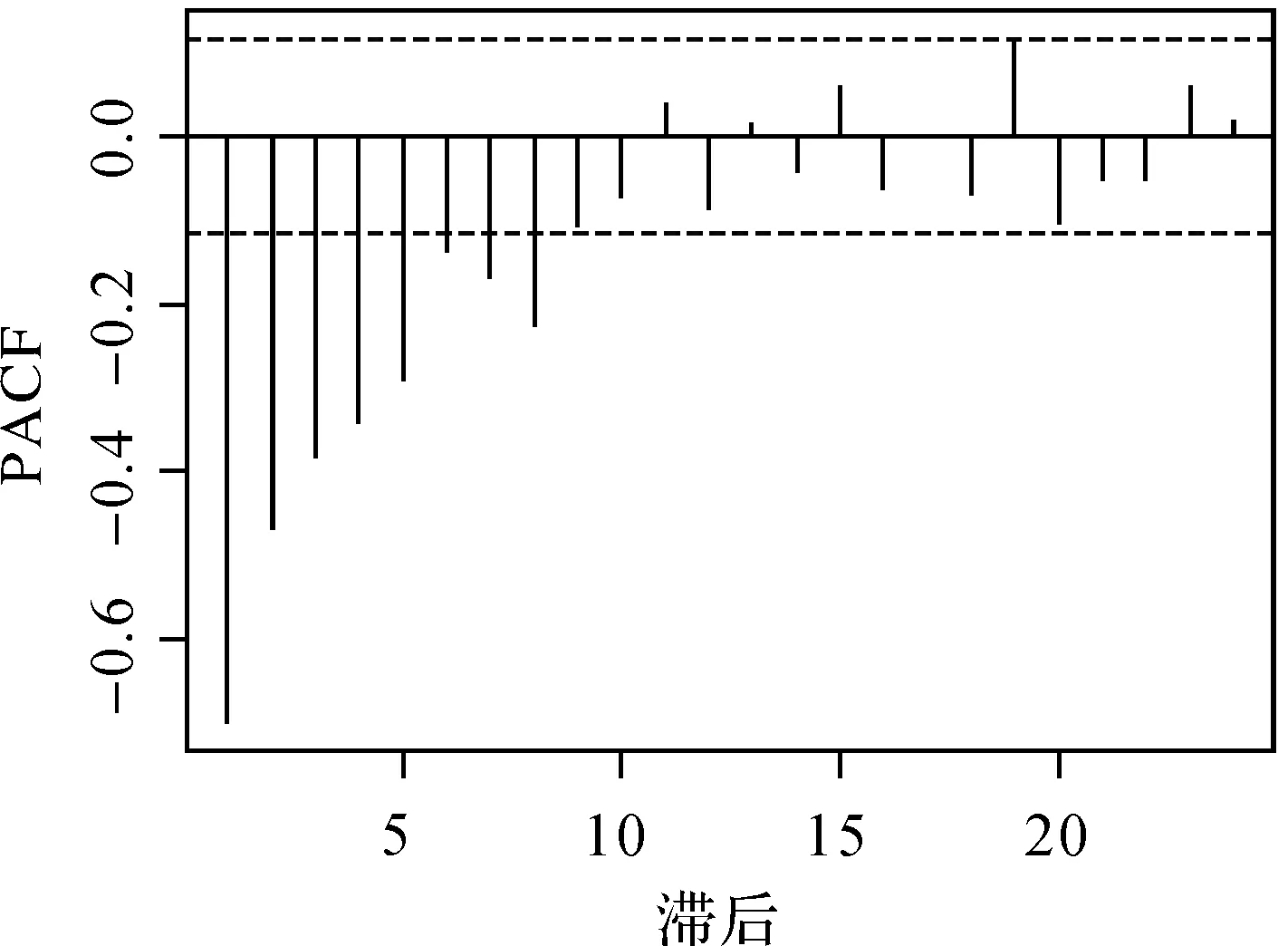
图7 二次差分钟差数据的偏自相关函数图Fig.7 Sample PACF of two differences clock errors data

由自相关函数和偏自相关函数的计算结果可知，偏自相关函数在8阶滞后以后截尾而自相关函数一直拖尾，故可认为两次差分后的序列服从AR(8)模型。

3.3 异常值探测分析

计算时发现，用本文算法处理此类两次差分后的钟差数据时，采用5σ原则可得到很好的异常值探测效果。为验证本文算法的有效性，在两次差分后的第100和第200个值上分别加上其数据本身的10倍和12倍的AO类异常扰动，分别为10×1.539 32×10-10和12×2.134 291 0-10。使用本文方法对序列中的AO类异常值进行探测，则pt和wt的计算结果分别如图8、图9所示。

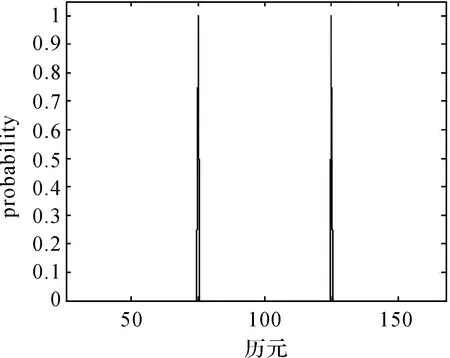
图8 钟差数据中单个异常扰动的pt结果Fig.8 pt of single outlier in clock errors data

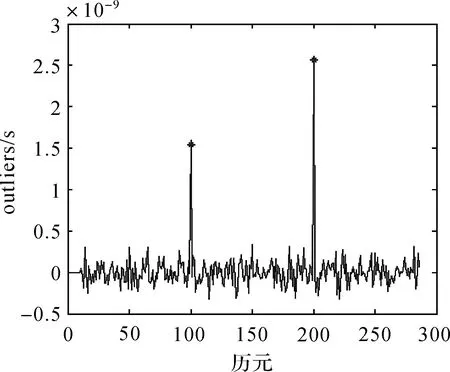
图9 钟差数据中单个异常扰动的wt结果Fig.9 wt of single outlier in clock errors data

由图8和图9可知，本文算法不但可以准确确定AO类异常值的位置，而且对相应异常扰动大小的估计也非常准确，具体异常扰动的估计值分别为：1.591 98×10-9和2.575 481×10-9。

对两次差分后的第100—105个历元的观测值分别加上大小为15×10-10的AO类异常扰动，以检验该算法对成片AO类异常值的探测效果，其pt和wt的计算结果分别如图10、图11所示。

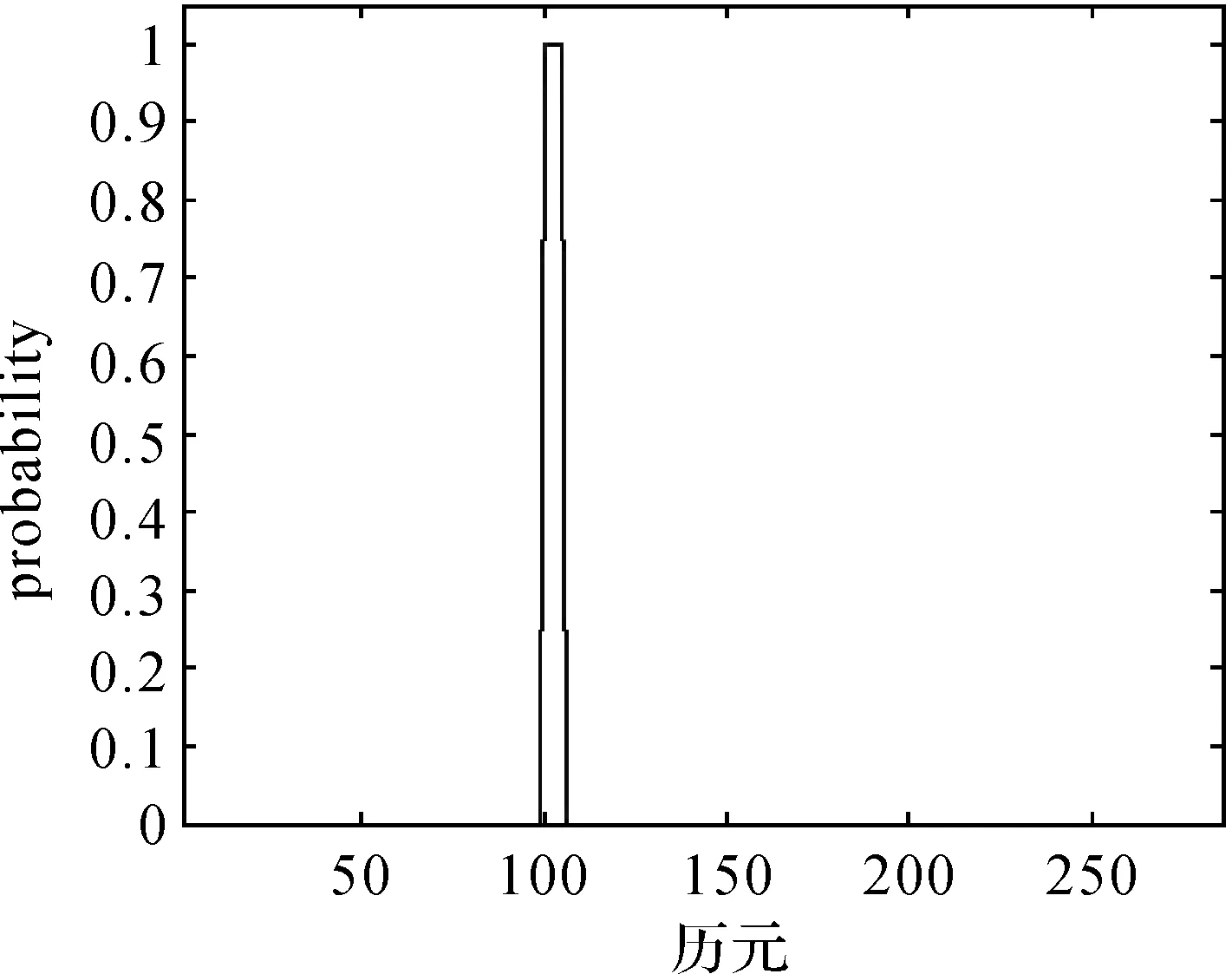
图10 钟差数据成片异常扰动的pt结果Fig.10 pt of patches of outliers in clock errors data

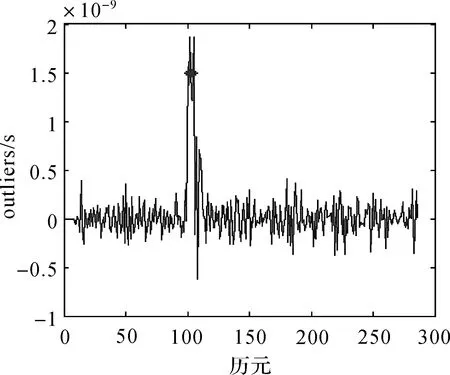
图11 钟差数据成片异常扰动的wt结果Fig.11 wtof patches of outliers in clock errors data

分析发现，本文方法对异常值的位置判断非常准确，对异常扰动的大小估计稍有偏差，异常扰动大小分别被估计为15.6×10-10、13.7×10-10、18.6×10-10、12.5×10-10、12.1×10-10、18.6×10-10。异常扰动的估计值虽有偏差，但是对于如此数量级的包含成片异常扰动的数据，得到如此的估计结果已属难能可贵。在计算过程中发现，算法具有很好的迭代稳定性，随着迭代次数的增加，估计精度逐渐增高并趋于稳定。另外，当成片异常扰动的数值变小时，异常扰动的估计效果变差；当成片异常扰动的数值变大时，异常扰动的估计效果变好。

3.4 钟差预报分析

差分前的IGS提供的钟差数据如果不包含异常值，本文算法不会启动异常扰动修复工作。此时可估计得到具体的AR(8)模型并依此对两次差分后的钟差数据进行预报，然后经过简单的反差分运算即可实现卫星钟差的预报。为了验证算法的钟差预报精度，利用实测数据的前200个历元进行模型估计和异常值探测，对后88个历元进行预报。则IGS提供的钟差数据和预报的钟差数据如图12所示。为了比较两者差异，将IGS提供的钟差数据和预报的钟差数据做差，其结果如图13所示。另外，为说明本文算法的有效性，利用二次多项式方法直接对后88个历元进行预报，给出预报结果与IGS提供的钟差数据的做差结果如图14所示。

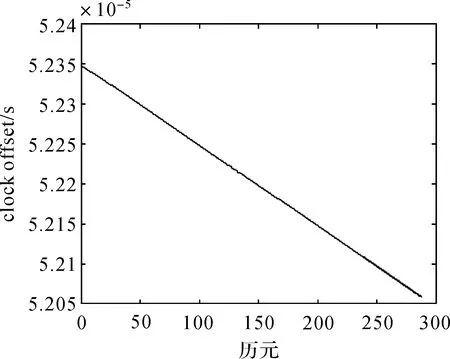
图12 IGS提供的钟差与预报钟差Fig.12 Clock errors of IGS and clock errors of prediction

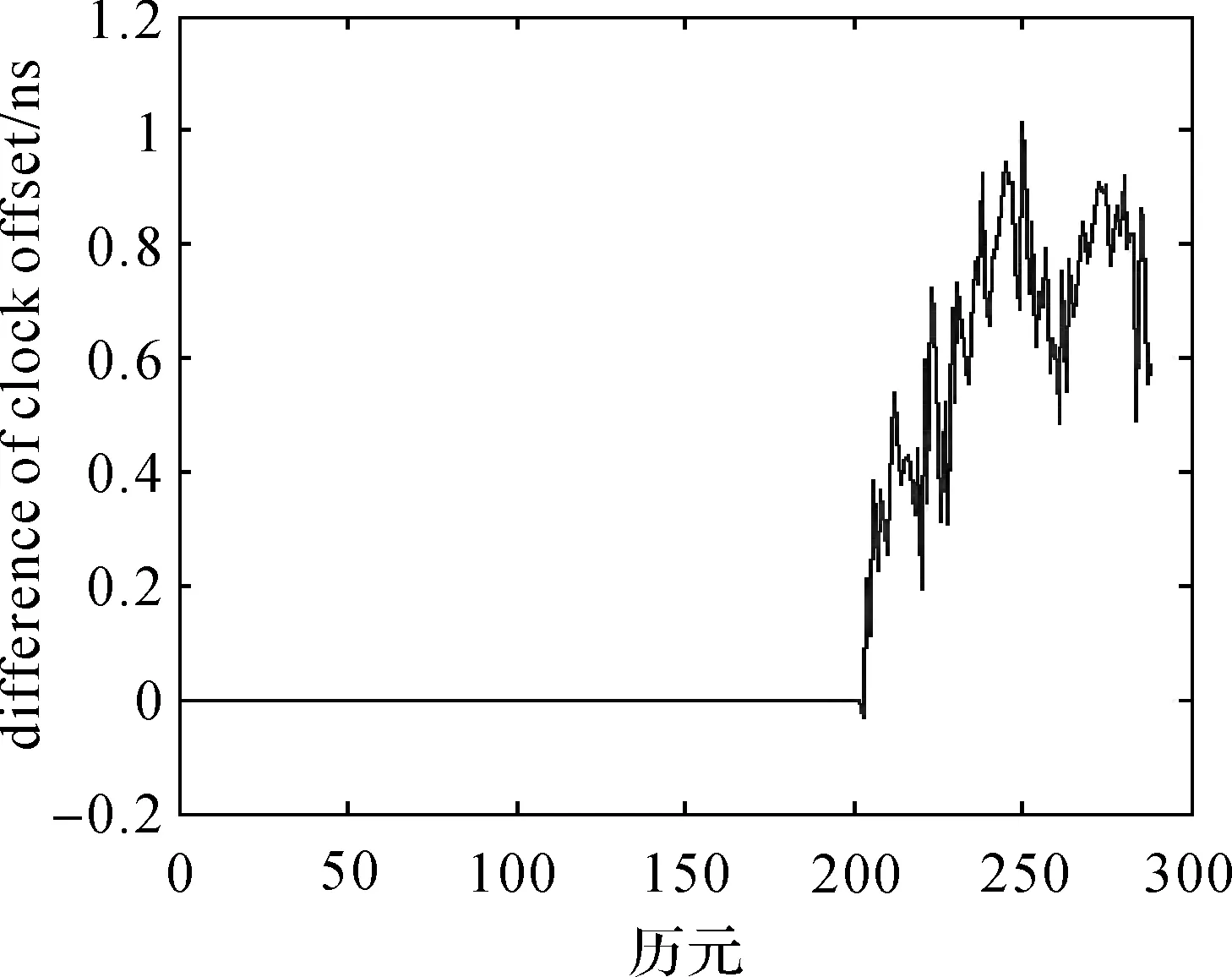
图13 IGS提供的钟差与预报钟差的差Fig.13 Difference between clock errors of IGS and clock errors of prediction

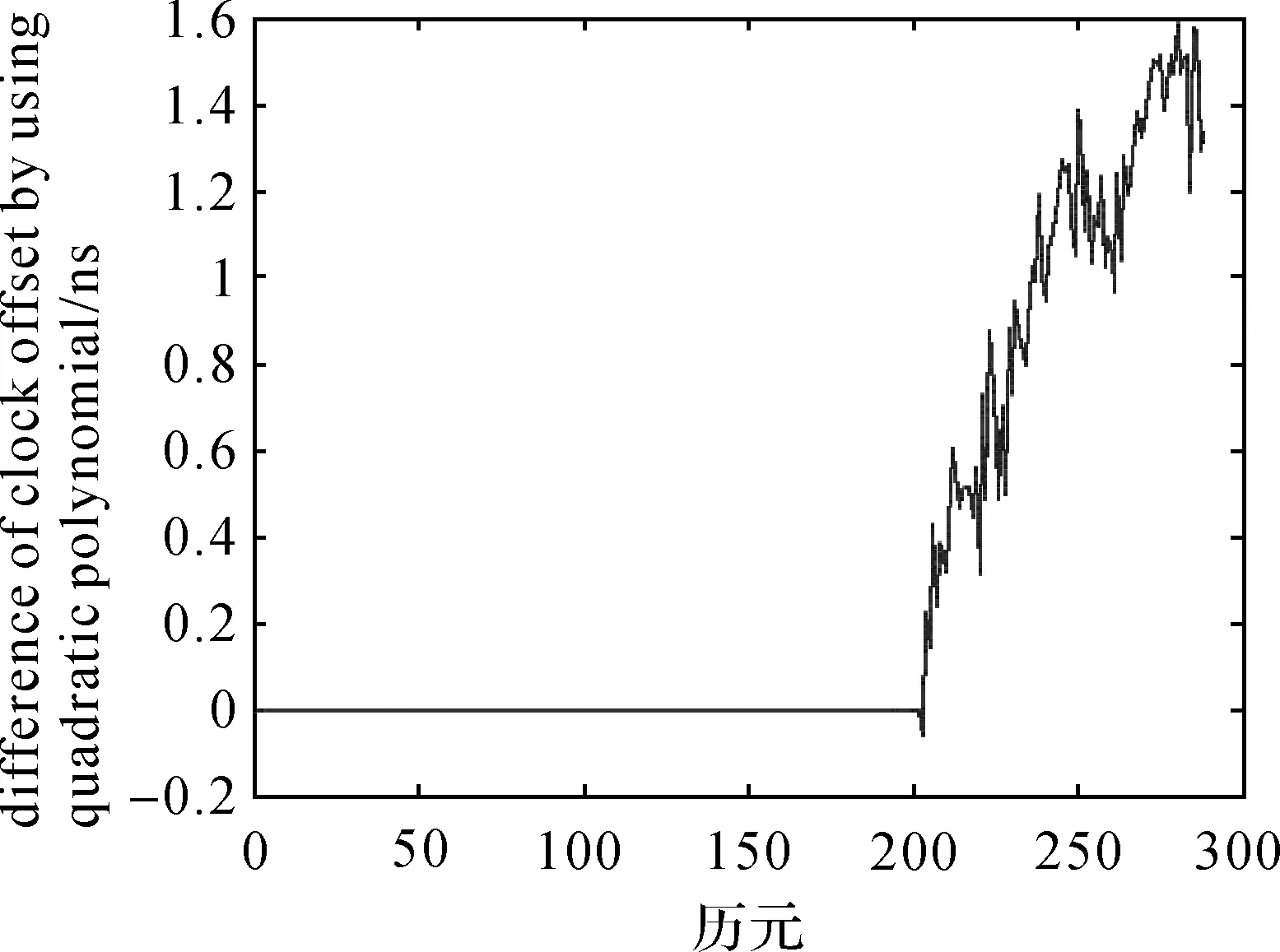
图14 IGS提供的钟差与多项式预报钟差的差Fig.14 Difference between clock errors of IGS and clock errors of prediction by using polynomial

由图12—14可以看出，没有异常扰动时，本文算法给出的钟差预报精度比较好。在图12中，数据的数量级为10-5，IGS提供的钟差数据与本文预报的后88个历元的钟差数据几乎完全重合，仅能看出两者之间微小的差异。在图13中可以看出，相对于单位秒而言，预报的后88个历元的钟差数据与IGS提供的钟差数据的差异的数量级是10-10。另外，对比图13和图14可以发现，本文算法的预报精度高于常用的二次多项式方法。

如果差分前的钟差序列含有异常值，则差分后异常值会出现淹没、掩盖或转移情况，使得差分后的异常值情况比较复杂。比如差分前的单个异常值，经过两次差分之后，将变为3个位置上相邻的成片异常值。而差分前的成片异常值，经过两次差分后，异常值情况更复杂。此处在差分前的钟差数据上，从第100个观测开始加上5个异常值，异常扰动的大小约为第100个观测值的10倍，即异常扰动的大小为5×10-4。则两次差分后，异常值的情况变为：第98、99位置上的5×10-4与-5×10-4、第103、104位置上的-5×10-4与5×10-4。经本文算法计算后，其pt和wt的计算结果分别如图15、图16所示。

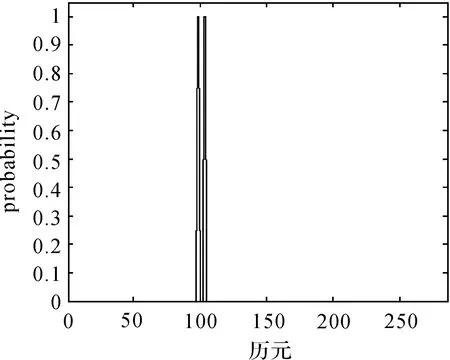
图15 原钟差数据成片异常扰动的pt结果Fig.15 pt of patches of outliers in original clock errors data

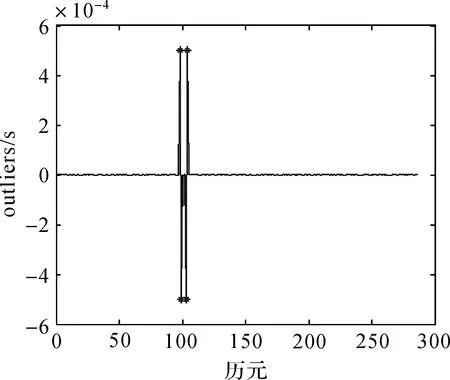
图16 原钟差数据成片异常扰动的wt结果Fig.16 wt of patches of outliers in original clock errors data

由图15、图16可以看出，本文算法的估计效果非常好，4个异常扰动的估计值分别为0.000 500 000 241 049 605，-0.000 500 000 289 798 94，-0.000 499 999 764 910 239，0.000 499 999 472 494 021。由此说明，不管差分前的异常值在差分后的平稳时间序列中如何变化，即不管差分后的平稳时间序列是包含单个异常扰动还是成片异常扰动，经过本文算法处理后均可有效消除异常值的影响。

为检验差分前的异常值对钟差预报的影响，同样从差分前钟差数据的第100个观测值开始加上5个大小为5×10-4的异常值，利用前200个历元进行模型估计和异常值探测，然后对后88个历元进行预报，并进行反差分运算。IGS提供的钟差数据和预报的钟差数据如图17所示，其中在分叉处向上的曲线是异常值修正后的预报钟差。将IGS提供的钟差数据和预报的钟差数据做差，其结果如图18所示。

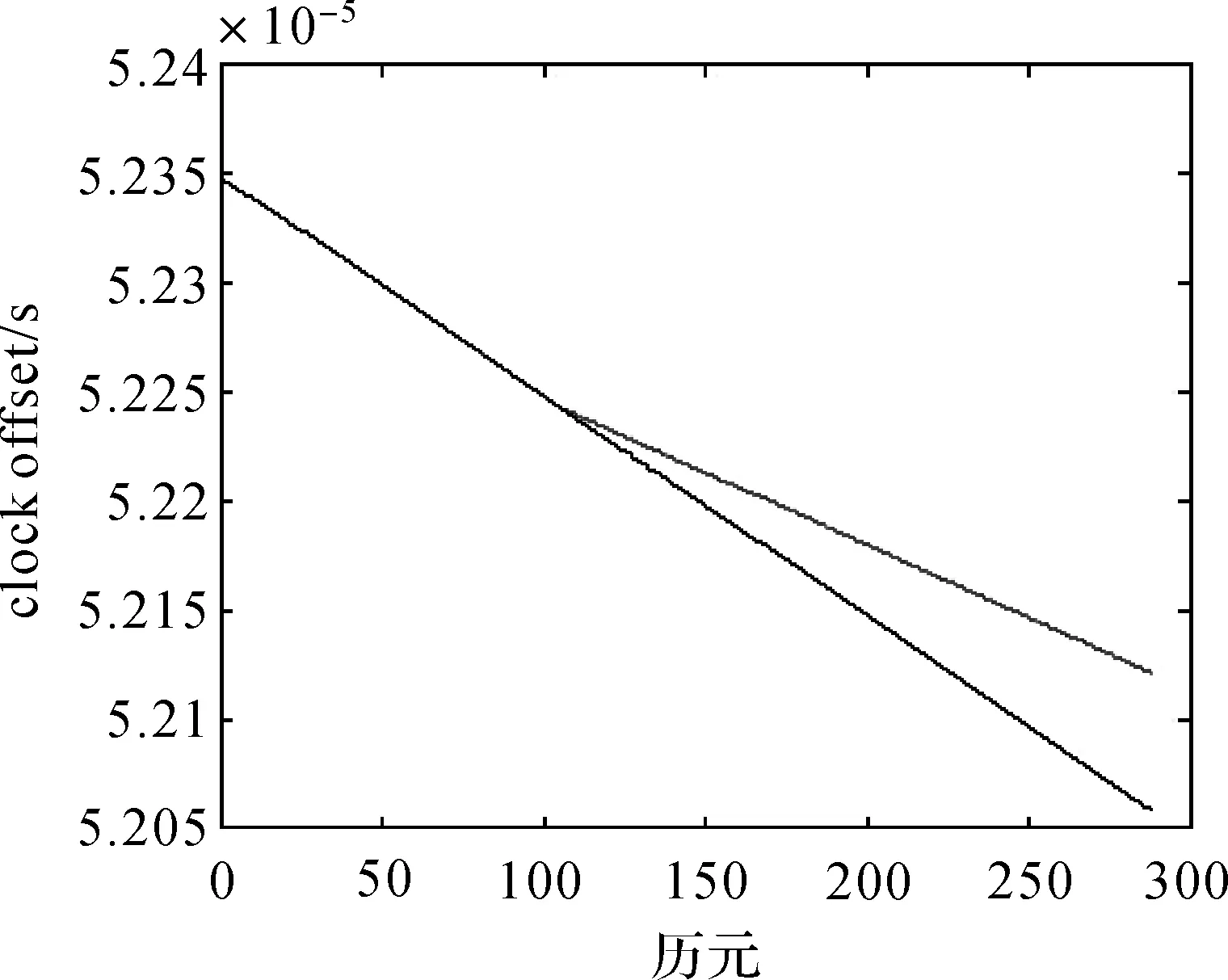
图17 IGS提供的钟差与含异常扰动的预报钟差Fig.17 Clock errors of IGS and clock errors of prediction with outliers

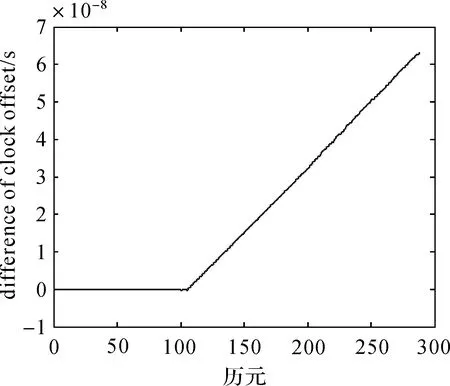
图18 IGS提供的钟差与含异常扰动的预报钟差的差Fig.18 Difference between clock errors of IGS and clock errors of prediction with outliers

相对于图12的情况，后88个历元的钟差预报精度降低了。从图18可以看出，此处数据的数量级是10-8，相对于图13中不包含异常值的情况，钟差预报精度降低了两个数量级。为说明此时钟差预报精度降低的原因，对于两次差分后的数据，修正其中异常值并预报后面数据，得到的结果如图19所示。

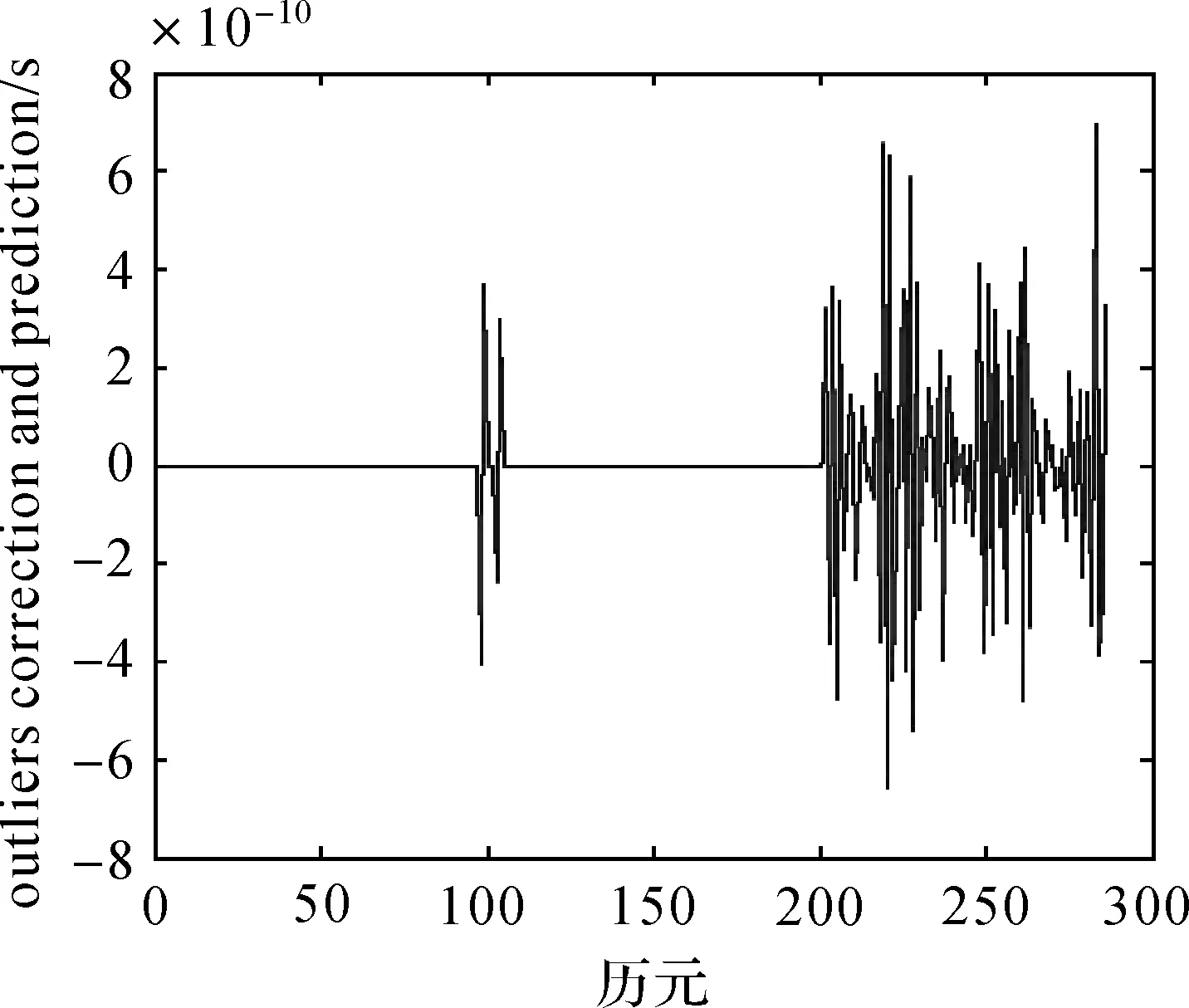
图19 两次差分的数据的异常值修正和预报情况Fig.19 Outliers elimination and prediction of two differences clock errors data

由图17—图19可以看出，虽然异常扰动大小的估计值非常准确。但是因为要经过两次反差分运算，使得两次反差分后得到的钟差数据，从第100个历元开始与IGS提供的数据出现了偏差，并且由于反差分运算的特性，这些偏差会逐步累加在反差分后的后续历元的观测值中。所以在钟差数据含有异常值的情况下，即使进行了很好的异常值探测与修正，经过反差分运算后，钟差预报的精度也会受到一定程度的影响。

由于本文算法可以很好地判定异常值位置。因此，不使用二次差分后含有AO异常值部分的数据，只利用第105个历元以后的数据进行反差分运算，得到的钟差预报结果如图20所示。

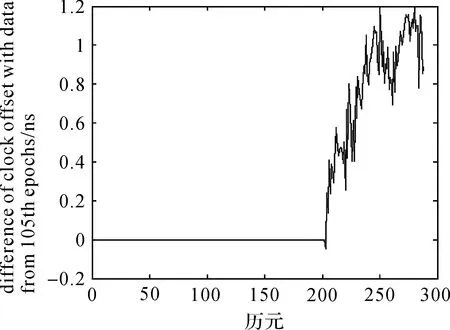
图20 用105历元以后数据的预报钟差与IGS提供的钟差的差Fig.20 Difference between clock errors of IGS and clock errors of prediction with data from 105th epochs

此结果与数据没有异常值的钟差预报结果非常接近。即使在数据包含异常值时，本文算法的钟差预报结果，仍然优于数据不包含异常值时多项式算法的预报结果。

4 结 论

本文首次将EM算法应用于AR模型中AO类异常值的探测问题，并提出了相应的异常值探测与修复算法。该算法不但可以处理单个异常值问题，而且可以有效消除成片异常值的影响。本文算法有以下优点：

(1) 本文算法可以同时估计AR模型系数、噪声方差、异常值位置和异常扰动大小，所有待估参数的估值均在同一个迭代过程中得到，具有较好的估计相容性。

(2) 本文算法有效解决了成片AO类异常值探测问题。只要σ的倍数选择得当，本文算法可以有效避免出现掩盖和淹没现象。

(3) 每一步迭代过程中均对原始观测进行修正得到纯净数据，并与原始数据共同参与估计的迭代过程，进而可以得到更准确的模型系数、噪声方差和异常扰动的估计值。

(4) 在异常扰动的判定过程中，不仅考虑了估计的异常扰动大小，而且考虑了估计的噪声方差，充分利用了异常扰动的相关统计信息。

(5) 本文算法的迭代稳定性良好，一般经过较少的迭代即可得到最终估计结果，随着迭代次数的增加，算法逐步收敛于函数极值，很少出现迭代发散的情况。

(6) 本文对于仿真数据采用的是3σ原则，对于实测的GPS钟差数据采用的是5σ原则。根据问题的具体情况，应当选择合适的σ原则的倍数，进而有效拓展该算法的使用范围。

在算法的实用性方面，本文将该算法应用于卫星钟差的异常扰动处理。采用本算法处理的卫星钟差观测序列，可以准确探测出观测序列中的AO类异常值，并同时拟合得到精确的AR模型，从而实现了对卫星钟差的高效、快速预报。