遥感影像融合AIHS转换与粒子群优化算法

陈应霞，陈 艳,刘 丛

1. 华东师范大学计算机科学与软件工程学院，上海 200062； 2. 长江大学计算机科学学院，湖北 荆州 434023； 3. 上海理工大学光电信息与计算机工程学院，上海 200082

Pan-sharpening是遥感影像融合技术中的一个重要分支，它是将不同来源同一对象的影像数据采用某种算法将影像中所包含的信息互补的数据进行有机结合产生新影像的技术，该技术在目标识别、计算机视觉、遥感、军事及智慧城市等领域有着广泛的应用，是当前遥感图像处理研究的热点。它可以分为3个层级：像素级、特征级和决策级，其中像素级是特征级和决策级的基础，也是目前主流的Pan-sharpening方法。本文研究的是基于像素级的Pan-sharpening方法。

目前，像素级Pan-sharpening方法大致分为3类。第1类是CS方法，也称之为组件替代法，如亮度-色度-饱和度(IHS)[1]、自适应亮度-色度-饱和度(AIHS)[2]、GramSchmidt[3-4]、Brovey[5]等。此类方法能获得较好的空间信息，但它们通常会产生光谱失真。第2类是多分辨率分析(MRA)方法[6]，如Wavelet[7]和Contourlet[8]等。与第1类方法不同，它是将全色图像(PAN)的高频细节加入到低空间分辨率的多光谱图像(LMS)中，同时对全色图像(PAN)进行采样，然后将采样图像与相应波段的多光谱图像(MS)进行Pan-sharpening。虽然MRA方法能在一定程度上减少光谱失真，但它却产生了空间退化现象，如混叠效应等[9]。第3类是近年来出现的基于变分的Pan-sharpening方法。该类方法首先建立一个总的能量泛函，然后对其进行优化，其最优化结果即对应着最佳的Pan-sharpening质量[10]，如P+XS[11]、VWP和AVWP[12]、SRIF[13]、文献[14]中的变分法等。它是Pan-sharpening领域的一个重大创新，但也存在一些缺陷，如在总能量函数优化过程中，其控制系数无法自动寻优，以至容易陷入局部最优，从而可能无法保证得到全局最优解。

为了解决以上问题，研究人员将上述Pan-sharpening方法与目前热门的群体智能优化方法相结合。如文献[15]提出了基于遗传算法(GA)的像素级加权平均法，他们将遗传算法和小波变换进行结合，试验结果表明与不使用遗传算法的方法相比，使用遗传算法的融合方法能得到更好的融合质量。文献[16]将亮度-色度-饱和度(IHS)与组合差分进化算法(CODE)进行结合，通过设置合理的进化算子和适应度函数，并对控制参数进行全局自动寻优，从而获得了最佳的Pan-sharpening效果。从现有的研究成果来看，目前基于智能优化的Pan-sharpening方法大多集中在空间域方面，而基于变换域的研究则相对较少。基于传统亮度-色度-饱和度(GIHS)的改进方法[2]和文献[14]中的变分Pan-sharpening以及文献[16]中的两个假设：①Pan-sharpening图像和原始MS图像具有相同的光谱信息；②Pan-sharpening图像与PAN图像包含的几何信息保持一致。本文提出了一种基于变换域的自适应亮度-色度-饱和度(AIHS)转换和粒子群算法(PSO)相结合的Pan-sharpening方法，称之为PAIHS。试验结果表明，该方法可以获得优化的自动控制参数，并在优化控制参数的约束下，利用AIHS转换可以获得优良质量的Pan-sharpening图像。

1 目标函数

传统亮度-色度-饱和度(GIHS)转换方法虽是一种计算高效且能获得高空间信息的融合方法，但它并不能很好地获得高光谱信息且会出现光谱失真现象，因此在提出方法之前需要做一些相关的工作以提高融合图像的保真度。

1.1 相关工作

1.1.1 改进自适应系数

M=(M1，M2，…，Mc，…，MC)(c=1,2,…,C)，表示多光谱图像M有C个波段，Mc是第c个波段的多光谱图像，Mc(x,y)是Mc中位置为(x,y)的一个像素；P表示为全色图像(PAN)；F=(F1,F2,…,Fc,…,FC)由多个未知的Pan-sharpening图像组成。

MS图像M的亮度分量I可以与MS图像之间建立一个线性关系[2,16]，这个关系描述为

I=∑cαcMc

(1)

式中，当多光谱图像为红、绿、蓝(RGB)三色时，αc的值为1/3。而事实上，大多数多光谱图像是由RGB和一个红外共4个波段组成，因此可以用αc=1/C表示4个及以上的多光谱图像的系数[16]。

由于亮度-色度-饱和度转换到红、绿、蓝(IHS-RGB)是用PAN图像的分量替换MS图像中I分量，因此，除去在替换过程中产生的误差以及由于图像本身存在的噪音和冗余信息外，MS图像的I波段的所有信息可以被全色图像所代替[2,16]，并结合式(1)，于是有

P≈∑cαcMc

(2)

式中，αc为未知系数。为了计算系数a，可以对函数G(a)进行最小化

λ∑c(max(0,-αc))2

(3)

式中，P(x)表示PAN图像处理函数；另外由于系数a非负，因此采用拉格朗日乘子λ来增加a的非负约束，目的是保证能获得较为理想的解[2]。

1.1.2 增强边缘保真度

由于IHS方法只对R、G、B3个分量进行转换和融合，导致4个及4个以上波段的图像在融合处理过程中会丢失很多的空间信息和光谱信息，尤其图像边缘的空间信息易丢失。解决这一问题，可以从PAN图像中提取边缘信息，然后与MS图像进行相应的Pan-sharpening，从而获得融合图像Fc[2,16]，描述如式(4)

Fc(x,y)=Mc(x,y)+h(x,y)(P(x,y)-I(x,y))

(4)

式中，h(x,y)是边缘检测函数，其定义为

(5)

式中，ε是一个很小的非零值；P(x,y)是PAN图像在(x,y)处的梯度；η是表示梯度大小的一个参数，其目的是形成边缘并控制图像的平滑度[2]。

1.2 目标函数设置

结合改进后的IHS方法[16-17]和文献[10,14]提出的Pan-sharpening变分模型，可以确立目标函数，然后优化这个目标函数来找重构最佳融合图像。

由于多光谱图像融合旨在结合全色图像PAN的空间细节和多光谱图像MS的光谱信息，得到空间分辨率和光谱分辨率兼优的高质量多光谱Pan-sharpening影像F[16,18]，故F空间域中的细节信息主要来自于PAN图像，而其光谱维的波段信息主要来自MS图像[10,14,16]，因此可以作以下2个假设：

(1) 保持空间信息策略。在式(2)中，描述的是MS图像与PAN图像之间的线性关系，这种组合约束对于提高融合图像的质量作用并不大，因此需要对其作进一步改进，建立PAN图像与Pan-sharpening图像F之间的关系，目的是尽可能地保留PAN图像的空间信息，从而提高融合图像的空间质量。文献[16]设计了PAN图像可以近似为Pan-sharpening图像F中每个波段图像的线性组合，即通过组合Pan-sharpening得到的图像F的全部波段的空间结构信息可以恢复成高分辨率PAN图像的细节信息，这种关联约束能很好地提高图像F的空间分辨率，但忽略了IHS转换过程中可能存在的光谱信息丢失，于是有

P≈∑cθcFc+δ

(6)

式中，δ表示光谱信息丢失量；θc为未知系数且0≤θc≤1，其目的是约束空间分辨率的保真度。

(2) 保持光谱信息策略。式(6)是为了丰富Pan-sharpening图像F的边缘几何信息，在一定程度上能提高融合图像的空间分辨率，但由于在第1个假设中，已经对空间质量进行了很好地约束，足以保证了Pan-sharpening图像F的空间分辨率，因此，还需要对图像F的光谱质量进行约束，从而避免出现光谱失真现象。文献[16]设计了MS图像可以近似看作Pan-sharpening图像F中的每个波段图像经过空间卷积操作后得到的采样图像的组合，即利用空间滤波滤除融合影像中的PAN结构信息后保留了多光谱图像的主要成分，但它忽略了采样过程中可能存在的空间信息丢失，于是有

Mc(x,y)≈∑i,jK(i,j)Fc(x-i,y-j)+φ

(7)

式中，φ表示空间信息丢失量；K为3×3的未知卷积模型。

这两个假设是基于遥感图像Pan-sharpening的基本原理，是在文献[10,14]等基础上演化而来，并在文献[16]中已得到了相关验证，其目的依旧是分别建立Pan-sharpening图像F与全色图像PAN以及与多光谱图像MS之间的关联约束。因此，根据这2个假设并结合式(3)可以确立需要优化的目标函数为

(8)

式中，第1部分即对应的是上述第1个假设，目的是保证Pan-sharpening图像F的空间质量；第2部分对应的是上述第2个假设，目的是保证Pan-sharpening图像F的光谱质量[16]。其中，1/C具有平衡作用，协同参数(α,θ,k)促使目标函数(8)向着最优解的方向快速收敛，从而确保获得最佳的Pan-sharpening结果。另外，图像F的最优值依据AIHS转换通过式(4)求得。

2 粒子群优化

2.1 粒子群算法

粒子群算法(PSO)采用群体智能优化策略，通过种群内粒子间的合作与竞争机制进行全局寻优从而获得全局最优解。该算法是由文献[19]首次提出来的。

在D维空间中，设定种群规模为NP，粒子i的位置表示为xi=(xi1,xi2,…,xiD)，粒子i的速度表示为vi=(vi1,vi2,…,viD)，f(xi)为适应度函数，pbesti=(pi1,pi2,…,piD)表示第i个粒子经历过的最佳位置，gbesti=(g1,g2,…,gD)表示所有粒子的全局最佳位置，并设定在第d(1≤d≪D)维的粒子位置变化范围限定在[Xmin,d,Xmax,d]，粒子速度变化范围限定在[-Vmax,d,Vmax,d]。

(1) 粒子i的第d维速度更新公式

(9)

(2) 粒子i的第d维位置更新公式

(10)

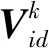
2.2 编码方式及种群初始化

编码的主要工作是将Pan-sharpening模型中的未知数映射成粒子的表达形式，常用的编码方式有二进制编码和实数编码。根据式(8)可知，需要求解的参数为{a1,a2,a3},{θ1,θ2,θ3}以及{K(1,1),K(1,2),K(1,3),K(2,1),K(2,2),K(2,3),K(3,1),K(3,2),K(3,3)}，因此本文采用实数编码的方式更为合理且算法的运行效率更高，其编码方式如图1所示。

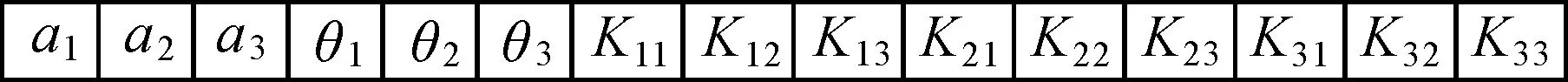
注：种群中的每个染色体(粒子)是随机生成的。图1 染色体编码方式Fig.1 The chromosome coding mode

2.3 技术流程

经过编码和初始化后，通过设定合理的算法收敛条件，并采用粒子群算法来优化式(8)，不断地迭代求解，从而可以获得全局最优解，即获得最佳控制参数和最优的Pan-sharpening图像。本文所采取的技术路线如图2所示。

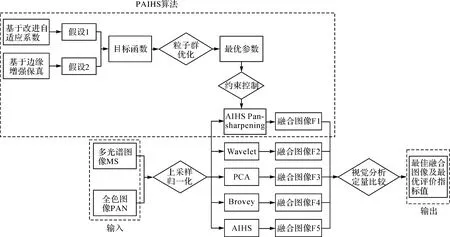
图2 技术流程Fig.2 The technology

2.4 PAIHS算法

这里主要介绍图2中的PAIHS部分，其基本算法流程如算法1所示。

算法1 PAIHS基本算法流程

输入：LMSM，PANP，c1，c2，r1，r2，w；

步骤1：根据AIHS和2个假设条件确定优化目标函数f(x)。

步骤2：设定粒子种群规模NP，粒子的维数D，算法的终止条件FES；设定xi∈[Xmin,d,Xmax,d]，vi∈[-Vmax,d,Vmax,d]；确定粒子编码方式，随机初始化种群，产生一组包含(α,θ,k)的解集合。

步骤3：根据F=AdaptiveIHS(M,P,α)计算融合图像F。

步骤4：对初始种群中的个体xi进行评估f(xi)min

H(α,θ,K)=∑x,y{|P(x,y)-∑cθcFc(x,y)+δ|p+

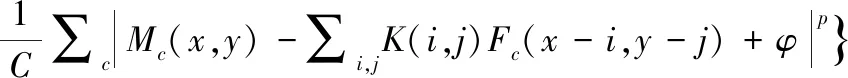
步骤6：比较每个粒子的适应度值f(xi)和它的个体最优值pbesti，若当前值particle(i).Posit优于个体最优值pbesti，则设particle(i).Posit为新的个体最优值。

步骤7：比较每个粒子的最佳适应度值和全局最优粒子的位置gbesti，若当前值particle(i).Best.Position优于全局最优粒子，则当设前值particle(i).Best.Position为新的全局最优粒子。

步骤8：计算评价指标R=imagemetrics(M,P,F)。

步骤9：判断代数FES是否已到达最大代数，如果已经到达，结束算法。否则转向步骤(3)。

输出：Pan-sharpening图像F；定量评价指标值R。

3 试验及对比分析

目前Pan-sharpening质量的评估方法有两种：主观评价方法和客观评价方法。主观评价法即根据人的视觉感知、大脑分析等机能特征对图像色彩、亮度、形状等作出一系列判断，并作出相应的分析和决策，也称之为视觉分析法。它是一种直观、简单灵活的判断方法，但该方法具有一定的片面性，因为观察者对色彩、亮度、模糊度、重影等现象的感知程度、理解能力、分析能力的不同，作出的判断结论可能存在一定的差异，这并不利于得到准确的评价结果。因此，除了进行主观评价外，还需要选取比较可靠的客观评价指标来进行定量计算，该方法也称之为定量分析方法。本文除了进行主观的视觉对比和分析外，还选取了CC[21]、ERGAS[21-22]、QAVE[23-24]、RASE[25]、RMSE[21]、SAM[14]、SID[16,26]这7个参数指标来进行客观评价。

3.1 视觉对比及分析

从整体视觉效果来看，图3—图5中的所有Pan-sharpening方法都能很好地将PAN图像的空间信息与MS图像的光谱信息集成到一起。相对于PAN图像而言，所获得Pan-sharpening图像F的解译能力都有了很大程度的提高，能够比较容易地分辨出图像F中的地物颜色和亮度等特征；相对于原MS图像，图像F中增添了大量的空间细节纹理信息，使得地物信息更为丰富。

图3采用了分辨率较高的MS图像，试验结果发现Pan-sharpening后的图像在视觉分析上辨别度不高，除PCA方法所得的图像颜色变红而失真明显外，其他3种方法所产生的图像在肉眼上难以分辨差异。于是在图4和图5中，采用了分辨率较低的MS图像进行试验，其视觉效果就产生了明显差异，对比及分析如下：

(1) 虽然Wavelet和AIHS方法所获得的图像在细节上表现最为丰富，但树木等地物存在明显颗粒感，出现了重影现象。

(2) 通过对比，不难发现Brovey方法所获得的图像是这5种方法中视觉效果最差的，如图4和图5中的树、道路和建筑物等都成团状、很模糊，基本看不清地物轮廓和纹理特征。

(3) 与PAN图像仔细对比，发现PCA方法获得的图像中间区域有较小程度的细节信息丢失，另外图像中的树木也有轻微模糊现象，而且整个图像偏亮，对比度也存在失真，因此存在光谱失真现象。

通过对图3—图5的视觉对比和分析，能直观地发现PAIHS方法得到的融合图像整体平滑、清晰、无明显重影和模糊现象。因此，在视觉上该方法是这5种方法中Pan-sharpening质量最好的。

3.2 定量对比及分析

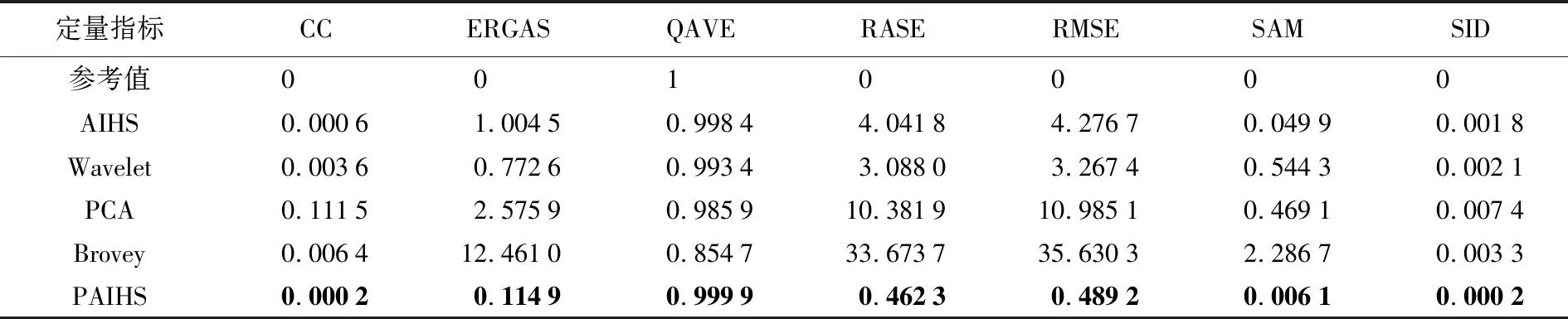
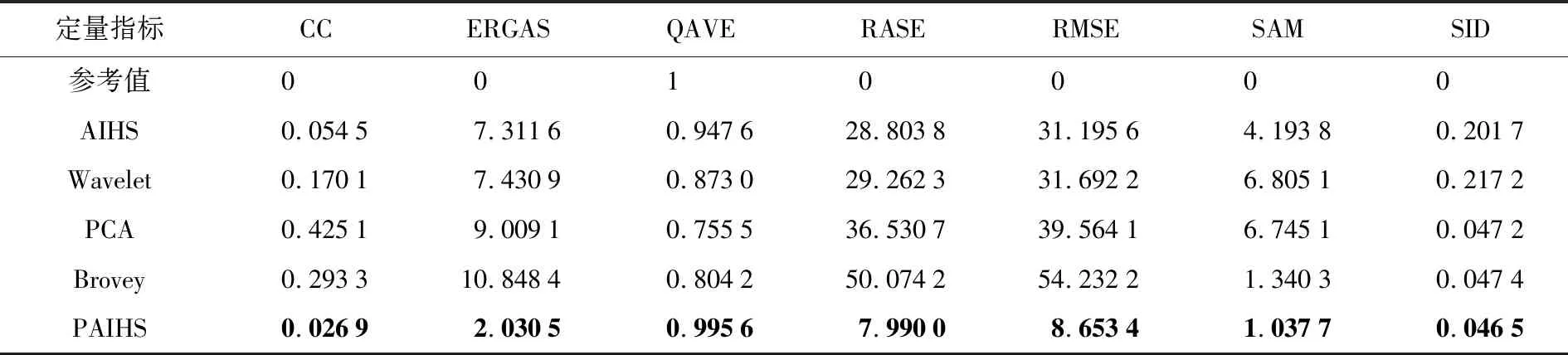
表1—表3是基于AIHS、Wavelet、PCA、Brovey及PAIHS的Pan-sharpening 5种方法的试验结果，其中的参考值和最好的评价指标值用粗体表示，其定量分析和比较如下。

图3 Pan-sharpened结果比较Fig.3 Comparison of Pan-sharpened results

图4 Pan-sharpened结果比较Fig.4 Comparison of Pan-sharpened results

定量指标CCERGASQAVERASERMSESAMSID参考值0 0 1 0 0 0 0 AIHS0.00061.00450.99844.04184.27670.04990.0018Wavelet0.00360.77260.99343.08803.26740.54430.0021PCA0.11152.57590.985910.381910.98510.46910.0074Brovey0.006412.46100.854733.673735.63032.28670.0033PAIHS0.00020.11490.99990.46230.48920.00610.0002

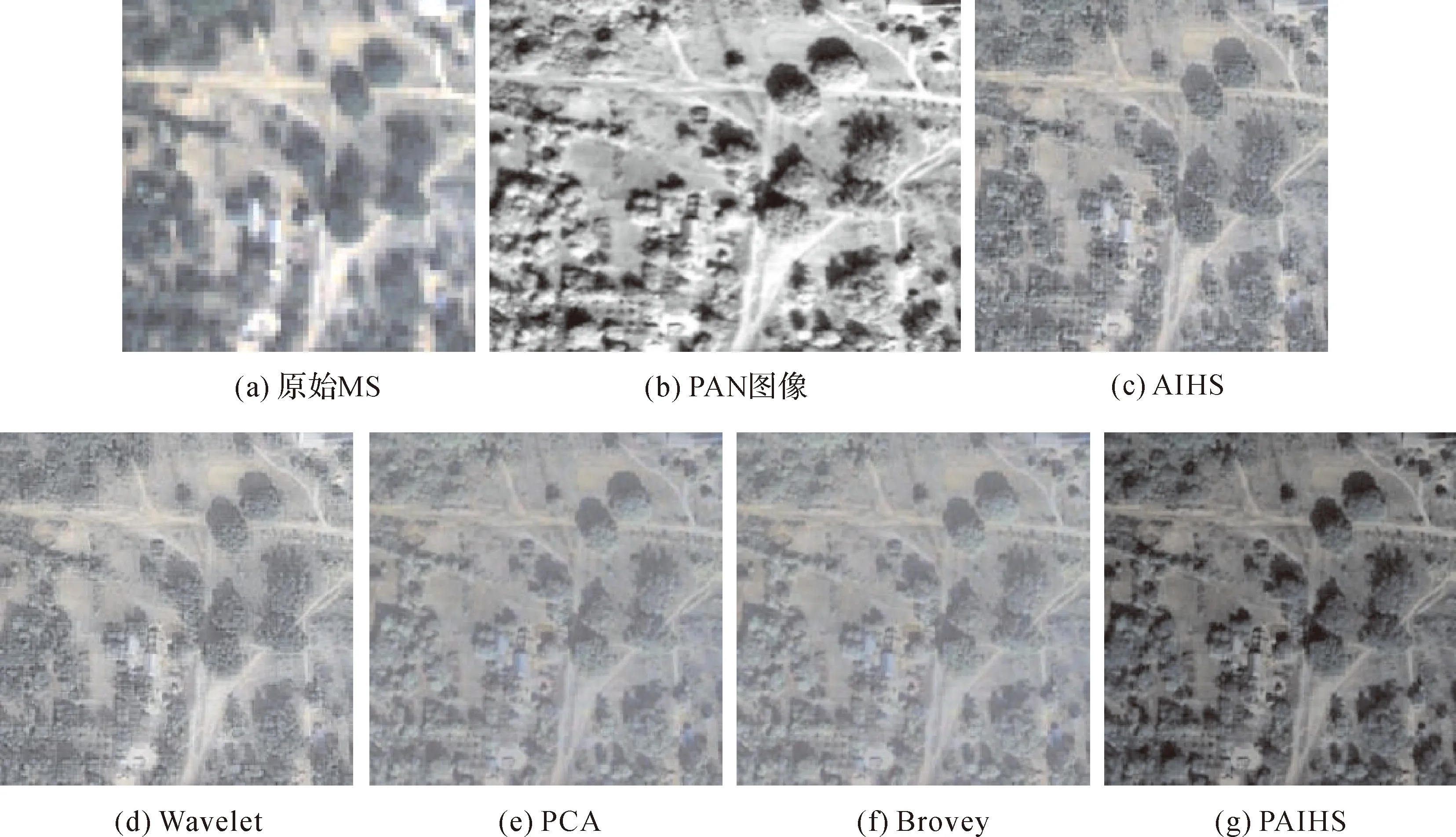
图5 Pan-sharpened结果比较Fig.5 Comparison of Pan-sharpened results

定量指标CCERGASQAVERASERMSESAMSID参考值0 0 1 0 0 0 0 AIHS0.05457.31160.947628.803831.19564.19380.2017Wavelet0.17017.43090.873029.262331.69226.80510.2172PCA0.42519.00910.755536.530739.56416.74510.0472Brovey0.293310.84840.804250.074254.23221.34030.0474PAIHS0.02692.03050.99567.99008.65341.03770.0465

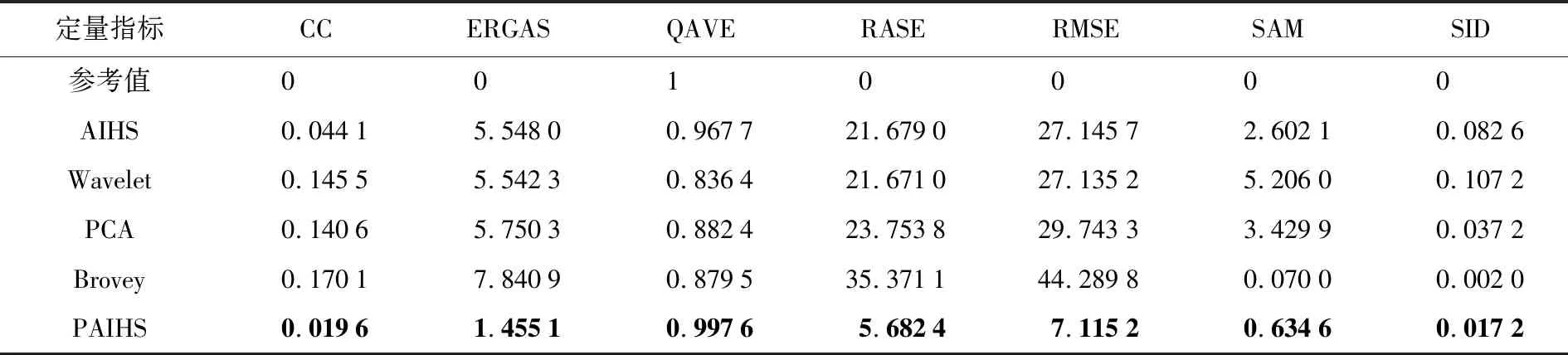
表3 图5的Pan-sharpening的定量指标结果

(1) 表1、表2中，PAIHS方法的各项指标值是5种方法中最好的。表3中，PAIHS方法的SAM值、SID值略差于Brovey方法，但是优于AIHS方法、Wavelet方法、PCA方法相应的指标值；除SAM值和SID值外，PAIHS方法的其他几种指标值仍是所有方法中最好的。因此，再一次印证了PAIHS方法的效果是最好的。

(2) 表1中，Brovey方法除CC值和SID值不是最差的外，其他5个指标值均是所有方法中最差的。表2中，Brovey方法的CC值优于Wavelet方法，但不及PCA方法；其SAM值略好外，QAVE值和SID值也比较居中，Brovey方法的ERGAS值、RASE值和RMSE值仍是所有方法中最差的。表3中的数值分布与表2类似。因此Brovey方法是所有方法中最差的，这与视觉分析得到Brovey方法是最差这一结论是一致的。

(3) 通过比较表1—表3发现，AIHS、Wavelet、PCA 3种方法的指标值时好时坏，比较中庸。3个表中，PCA方法的ERGAS值比另外两种方法的ERGAS值差，PCA方法的QAVE值除在表1和表2中也是3种方法中最差的，而ERGAS值和QAVE值是光谱失真的评价指标，这与视觉上得到的对比度失真、图像整体亮度偏亮的结论是相吻合的。

通过主观分析和客观评价参数的对比，可以发现PAIHS方法比其他4种融合方法好。另外，在试验中也得出一个结论：种群规模设置越大，迭代次数越Pan-sharpening质量越好。

4 结 论

本文提出了一种Pan-sharpening方法，称之为PAIHS。该方法基于自适应亮度-色度-饱和度(AIHS)转换和变分Pan-sharpening框架及2个假设，同时确定了优化目标函数，然后采用粒子群优化算法进行优化，目的是寻找全局最优控制系数，确保能较好地保持原MS图像的光谱信息和PAN图像的空间细节信息，从而获得最佳质量的Pan-sharpening图像。另外，文中将提出的方法与目前主流的Pan-sharpening方法通过3幅遥感图像进行试验对比。试验结果表明，本文方法所得的融合图像在光谱特性的保持能力和空间细节信息的表现方面都有更好的效果，是一种有效且可行的Pan-sharpening方法。