基于ADVISOR的纯电动汽车驱动转矩双模糊控制策略

赵 涛，李 强，邢紫筱，张强华

(1.浙江科技学院 机械与能源工程学院，杭州 310023；2.爱丁堡大学 工程学院，爱丁堡 EH8 9YL；3.宁波均胜科技有限公司，浙江 宁波 315000)

近几年，纯电动汽车具有污染少、能耗低、噪音小等优点，得到世界各国政府的大力支持，不少科研机构和相关企业纷纷掀起了致力于研发高性能纯电动汽车的热潮。而驱动系统作为纯电动汽车的核心部分，一定程度上决定了电动汽车的动力性和经济性。国外对纯电动汽车驱动系统的研究起步相对较早[1-2]。国内科研院所和高校对控制系统进行了大量研究与开发[3-6]，也取得了丰硕的成果。姚海峰等[7-8]提出的驱动转矩控制策略在一定程度上满足高速工况下的动力需求，但未考虑加速踏板变化率对车辆加速性能的影响。动力电池储能技术、驱动系统的性能及传动效率等限制了续航能力和能量利用率；邓元望等[9]考虑了短时踏板开度变化率对车辆加速性能的影响，提高了车辆的操控性和快速性，但同时也加大了对动力电池的消耗；薛涛等[10]对纯电动汽车进行了动力性匹配研究，但未考虑从控制策略方面提升动力性和经济性。

为更好解决驾驶员操作在不同行驶工况下存在一定非线性和时不变性的问题，通过建立整车动力学模型及驾驶员输入参数模型，包括车辆行驶动力学模型、功率平衡模型、加速踏板模型、动力电池模型，并且考虑控制加速踏板开度变化率等因素，采用双模糊控制器，我们提出了以基本转矩和补偿转矩为电机输出等控制策略，基于ADVISOR平台进行了整车仿真与分析。结果表明，所设计双模糊控制器可有效提高车辆动力性及动力电池使用效率。

1 纯电动汽车动力学模型

纯电动汽车驱动系统将驱动电机输出的转矩经机械传动系统传递给驱动轮驱动汽车行驶。它主要包括：驾驶员操作系统、整车控制器、能源系统、电机驱动系统及机械传动系统，具体架构如图1所示。

图1 纯电动汽车动力驱动系统架构Fig.1 Architecture of power drive system of pure electric vehicle

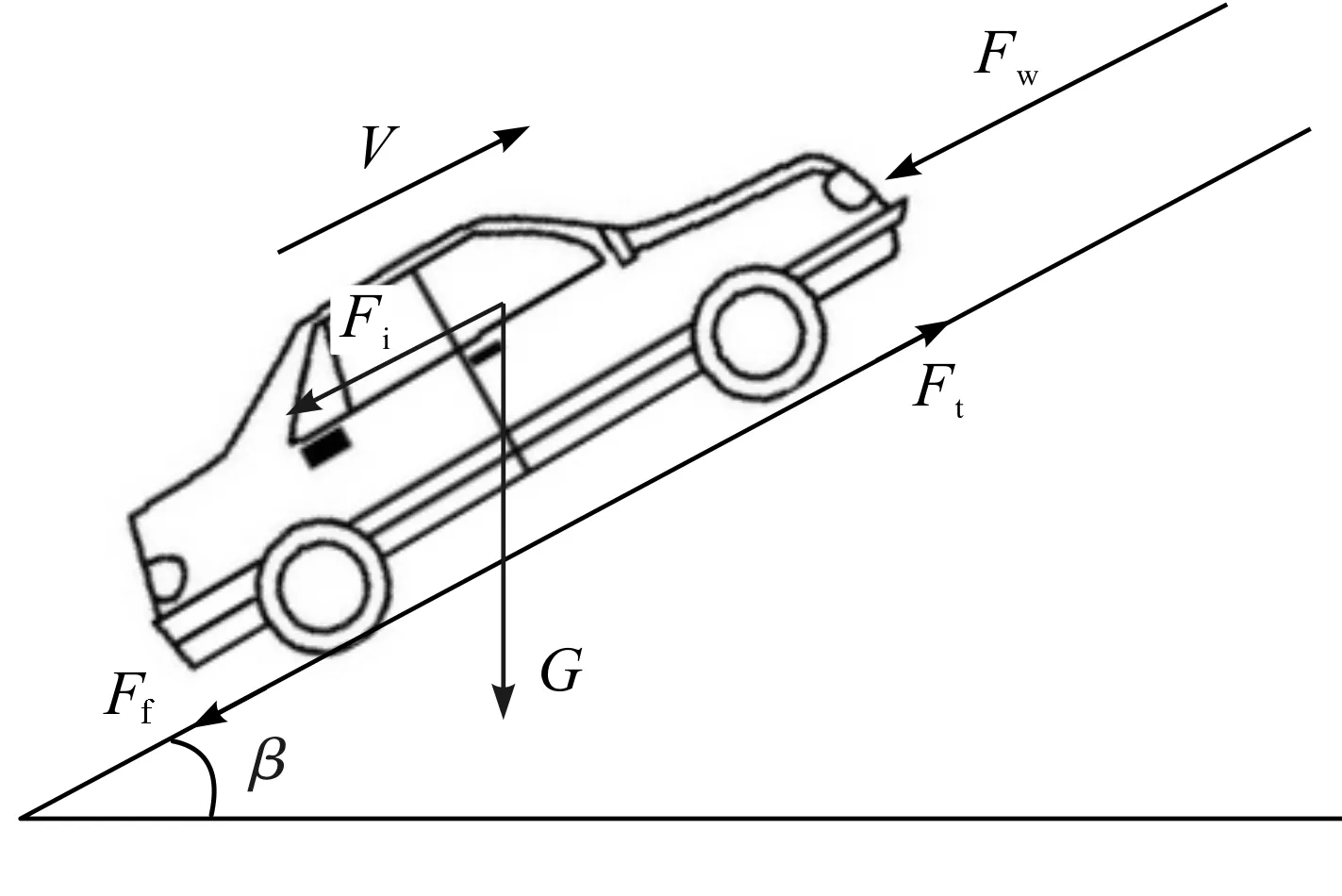
图2 汽车行驶动力学模型Fig.2 Vehicle driving dynamics model

1.1 行驶方程式

确定后驱汽车的行驶方程以分析汽车行驶方向的运动状态。Ft表示驱动力，行驶阻力包括滚动阻力Ff、空气阻力Fw、坡度阻力Fi、加速阻力Fj。汽车行驶动力学模型如图2所示。

由图2建立汽车行驶方程式：

Ft=∑F=Ff+Fw+Fi+Fj。

(1)

选择坡度为β的路面，汽车以速度v0在极限附着力Fmax的驱动下行驶，当前步长Δt内汽车所能产生的最大速度为vt，则当前步长内汽车的加速度为：

a=(vt-v0)/Δt。

(2)

当前步长内汽车的平均速度vaver为汽车当前的需求车速，由当前步长内汽车的始末速度v0、vt计算得：

vaver=(v0+vt)/2。

(3)

将式(1)～(3)联立并利用数值迭代法求得汽车极限附着驱动力下能够提供的最高车速vmax：

(4)

式(4)中：m为整车质量，kg；μmax为附着极限；b为质心到后轴距离，m；L为轴距，m；f1为前轮滚阻系数；β为坡度，(°)；f2为后轮滚阻系数；ρ为空气密度，kg/m3；CD为空气阻力系数；A为迎风面积，m2；hg为质心高度，m。

1.2 功率平衡方程

纯电动汽车行驶时不仅驱动力和行驶阻力平衡，电机功率与阻力功率也要相平衡。换言之，在纯电动汽车行驶过程中的每一时刻，电机的输出功率总是等于行驶阻力功率与机械传动损失功率之和[11]。纯电动汽车行驶阻力功率Pm一般包括滚动阻力功率Pf、空气阻力功率Pw、坡度阻力功率Pi和加速阻力功率Pj。功率平衡方程为：

整车的动力系统最高总功率Pmax由最高车速vmax确定：

2 驱动输入系统建模

2.1 加速踏板模型

图3 加速踏板开度与输出电压值对应关系曲线Fig.3 Corresponding curve of accelerating pedal opening and output voltage value

纯电动汽车加速踏板可采用电位计测量踏板开度，加速踏板的不同角度对应不同的输出电压，角度越大，电压值一般越高。加速踏板安装固定后，对其角度与输出电压值进行测试校准，多次测量取均值后得出两者间的对应关系，如图3所示。

理想对应关系呈一定线性，但顾及驾驶员的可操作性及控制器模型的有效性，暂不考虑踏板高低极限位置时的函数关系，即开度小于5%和大于90%时的情况。根据有限的若干个测量点的数值，利用最小二乘法进行曲线拟合，得出输出电压f(x)与其踏板开度x间的关系：

f(x)=4.872×exp(-((x-104.8)/68.05)2)
(5%≤x≤90%)。

(5)

测得的实际电压值与通过函数拟合的电压值相对比，满足偏差在±3.5%以内的要求。这是由于实际中加速踏板传感器的采集有一定的误差，但对电机控制器输出转矩分辨率而言，该误差可以忽略不计。

2.2 动力电池模型

动力电池的能量存储及充放电速率是制约其发展的关键技术，所选高性能的锂电池作为能量源，额定电压为310 V，容量为220 A·h，共96串，根据所选的动力电池的理化特性，建立电池的充放电模型为：

(6)

式(6)中：it为提取容量，A·h；i*为低频电流动态，A；i为电池电流，A；E0为电池恒压，V；K为极化常数，A/h；k为系数，充电时为0.1，放电时为1；Q为最大电池容量，A·h；A1为指数电压，V；B为指数能力，A/h。

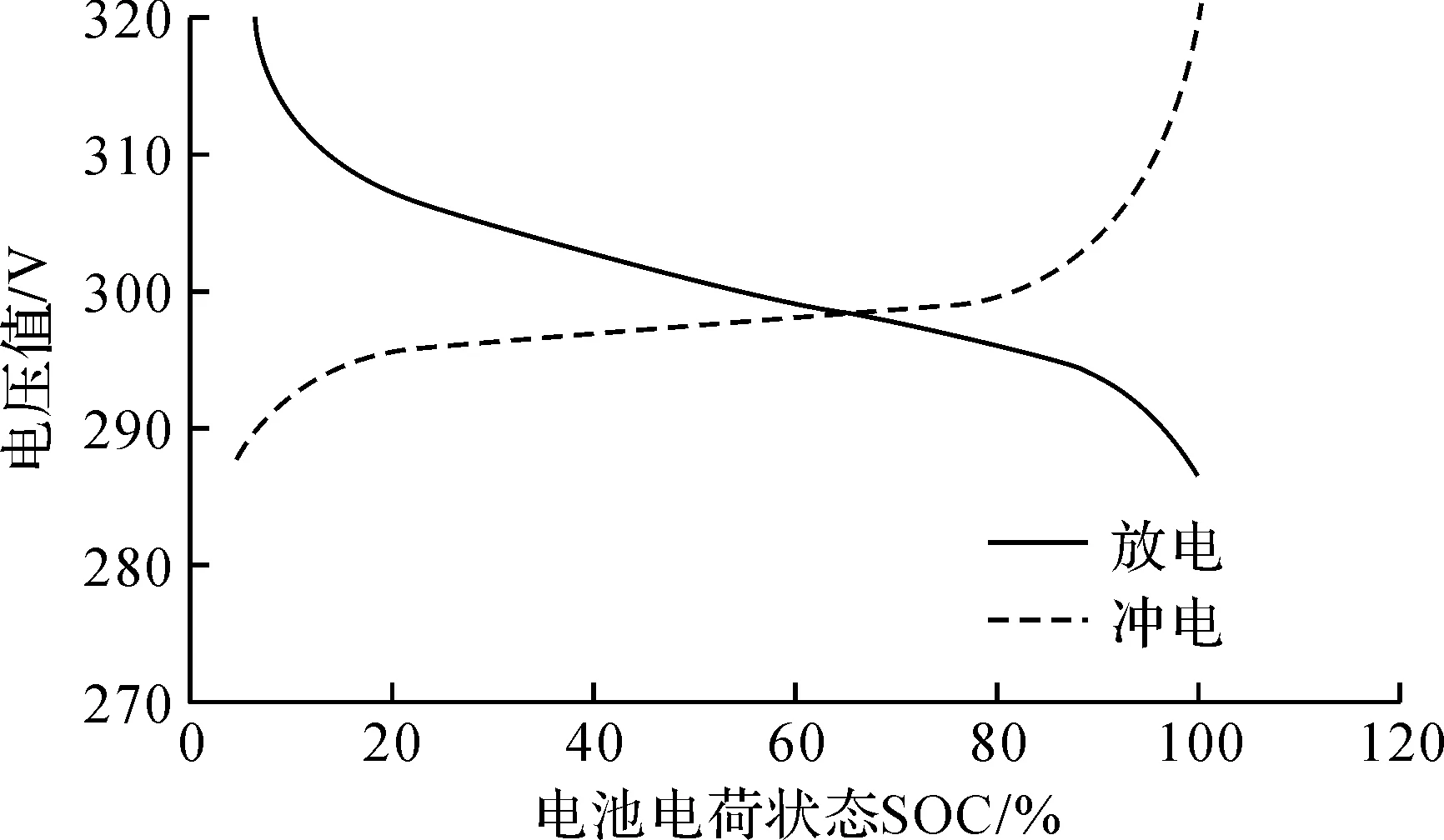
图4 电池充放电曲线Fig.4 Charge-discharge curve of batteries

所得试验测试数据经拟合后充放电曲线如图4所示，充电电压最大值约为320 V，最小值约为280 V。

蓄电池组输出的功率受到等效电路传递的最大功率和电机最大工作功率的限制，二者要取其较小值。动力电池荷电状态(state of charge，SOC)表示剩余容量，是直接反映电池持续供电能力和状况的一个重要参数，常用百分数表示。采用安时计量法[12]建立SOC状态预测算法：

(7)

3 电动汽车驱动系统控制策略

通过电机输出转矩的控制策略，可使纯电动汽车的动力性能得以改善，提高续驶里程。复杂的行驶工况导致加速踏板开度变化率会对动力性产生一定的影响，因此将电机的输出转矩T分为基本转矩T1与补偿转矩T2[13-14]两部分。基本转矩T1与加速踏板开度Ka间存在一定的比例关系，同时还需考虑动力电池电量SOC和电机转速n的影响；补偿转矩T2通过分析加速踏板开度Ka及其变化率dKa后计算得出。驾驶意图判断模块对来自驾驶员模块的加速踏板开度Ka进行解析后，经基本输出模块输出基本转矩T1。同时，信号处理模块采集加速与制动踏板的位置并解析出当前踏板变化率及开度信息，输入模糊控制器中求解补偿转矩T2。此外，双模糊控制器还将实时采集当前的SOC等状态信息，从而对电机的输出功率进行限制。驱动系统转矩控制策略如图5所示。

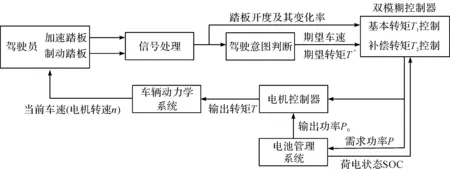
图5 纯电动汽车驱动系统转矩控制策略Fig.5 Torque control strategy of pure electric vehicle driving system

3.1 基本模糊控制器设计

由于驾驶意图复杂多变且非线性，不易获得精确数学模型，因此采用模糊控制方法求解电机转矩输出值。此部分所设计的模糊控制器包括三个输入变量：当前电机转速Nm，动力电池荷电状态SOC(%)和加速踏板开度Ka(%)，输出量为电机输出转矩T1(N·m)。加速踏板的开度范围为0%～100%，但为避免加速踏板的误操作以及消除自由行程误差，设置其下限值为5%，同时为安全性考虑，设置其上限为90%，因此论域为[5，90](%)。由所选电机特性取其转速论域为[0，8 000](r/min)，电池电量的论域为[20，95](%)，输出转矩的论域为[30，90](N·m)。

对输入输出参数作模糊化处理，Nm={NL，NS，ZO，PS，PL}，SOC={NL，NS，ZO，PS，PL}，Ka={NL，NS，ZO，PS，PL}。选择模糊控制器的输入输出隶属度函数，并通过该隶属度函数设计模糊控制规则，最后利用重心法将模糊输入量转换为精确的转矩输出[15-16]。解模糊得出当3个输入参数中一个为定值时，输出转矩与另外2个参数的对应关系如图6所示。

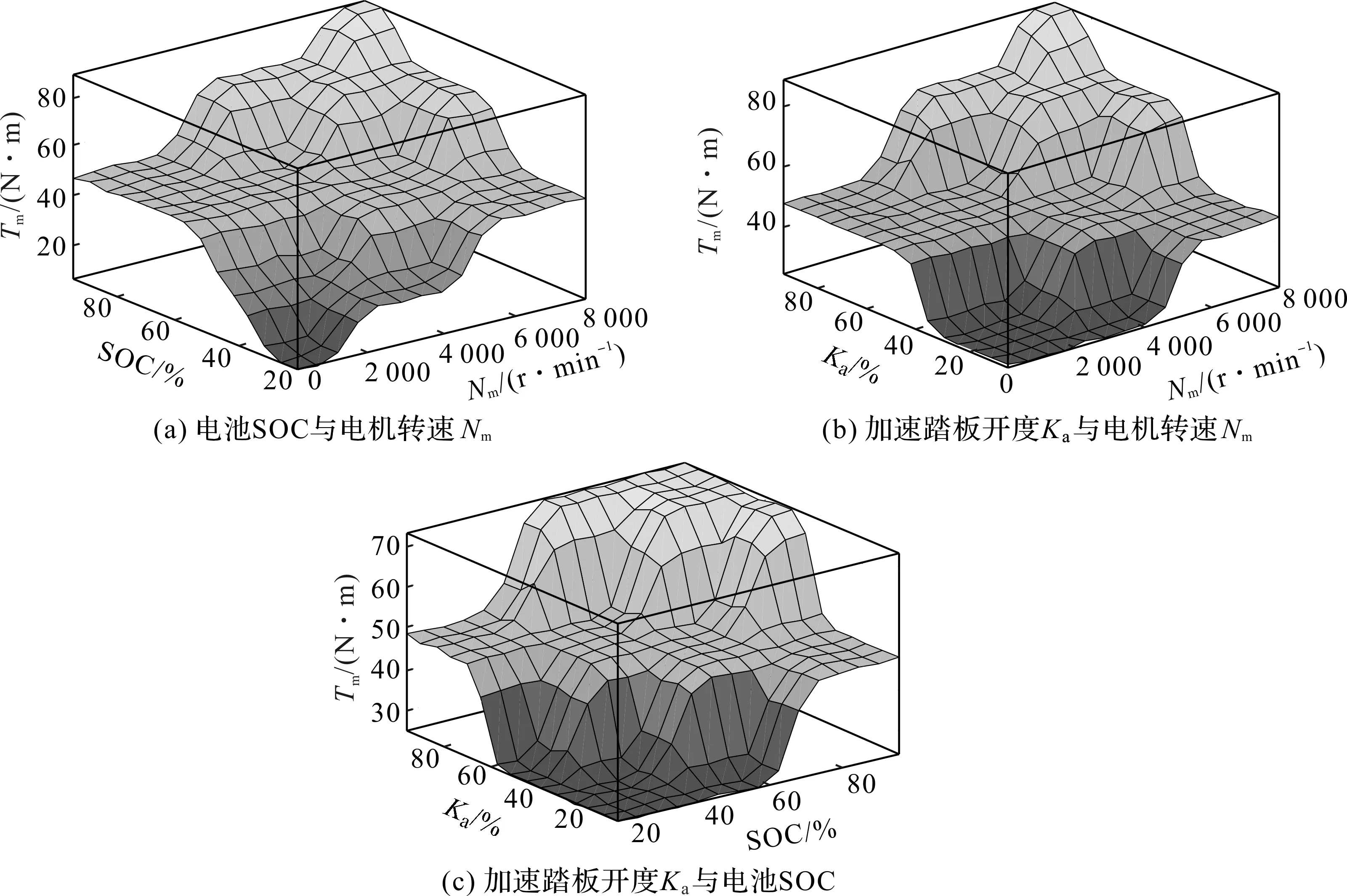
图6 控制器中电机转矩输出特性曲线Fig.6 Torque output characteristic curve of motor in controller

由图6(a)可知，当电机转速平稳时，输出转矩随SOC增大后趋于平缓，且转速越高，输出的转矩值越大；当SOC固定时，输出转矩随转速的增大而增大。由图6(b)可知，当输出转速不变时，电机输出转矩随加速踏板开度的增大而增加，后趋于平缓；而当加速踏板开度固定时，电机输出转矩随转速的增加而增加，并在末端趋于平缓。由图6(c)可知，当电池SOC一定时，电机输出转矩随加速踏板开度增大先增加后平缓，同样，当加速踏板开度固定时，电机输出转矩亦随SOC增加而增加。

3.2 补偿模糊控制器设计

考虑加速踏板的开度变化率对电机输出转矩的影响，使用补偿转矩为车辆提供速度变化时的额外转矩输出以便迅速响应驾驶员意图。补偿转矩规则：低速时加速踏板单位正向变化量对应的补偿转矩大于高速时加速踏板单位正向变化量对应的补偿转矩；高速时加速踏板单位反向变化量对应的转矩减小量大于低速时加速踏板单位反向变化量对应的转矩减小量。此部分所设计的控制器包括两个输入变量加速踏板开度Ka(%)及其变化率dKa和输出量补偿转矩因子KT。加速踏板开度Ka的论域仍为[5，90](%)，开度变化率dKa的论域为[-100，100](%)。补偿转矩因子KT与加速踏板开度变化率dKa之间存在一定比例关系，其论域为[-100，100](%)，dKa为正表示补偿转矩大于0；反之则小于0。

图7 补偿转矩因子KT与加速踏板开度Ka及其变化率dKa的关系Fig.7 Relationship between compensation torque factor KT and acceleration pedal opening Ka and its change rate dKa

对输入输出参数作模糊化处理，Ka={NL，ZO，PS，PL}，dKa={NL，NS，ZO，PS，PL}，KT={NL，NS，ZO，PS，PL}。模糊控制器的推理系统采用Mamdani类型，输入输出隶属度函数选择高斯型，采用重心法使模糊量清晰化，最终得补偿转矩因子KT与加速踏板开度Ka及其变化率dKa的对应关系，如图7所示。

根据双模糊控制器输入条件与输出转矩之间的关系，可计算出某一状态下驾驶员期望的转矩输出值T，其值为基本转矩T1和补偿转矩T2之和。基本转矩可由基本模糊控制器的输出直接确定，补偿转矩值为补偿转矩因子KT与电机额定转矩Te的乘积。

4 纯电动汽车驱动系统性能仿真分析

某型号车辆仿真模型的主要技术参数如表1所示。

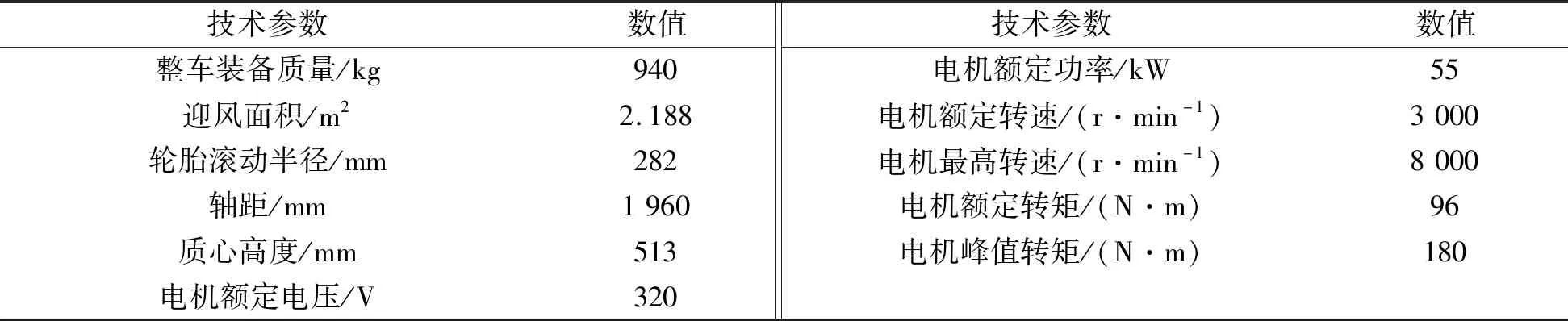
表1 某型号纯电动汽车主要技术参数Table 1 Main technical parameters of a pure electric vehicle

根据所建立的驱动系统模型，在MATLAB/Simulink下搭建包含双模糊控制器的纯电动汽车驱动系统模型，为了进一步研究纯电动汽车动力性和电池利用率之间的关系，分别选用车速高、驾驶平稳的CYC_HWFET高速工况和中低速CYC_DUDC典型额外城市工况[17]。前者工况全长16.51 km，运行时长765 s，后者工况全长10.93 km，运行1 225 s，并设置循环次数为13。利用高级车辆仿真器ADVISOR，基于Simulink进行二次开发的模块对使用模糊控制器车型的动力性和SOC状态进行仿真，结果如图8～11所示。

图8 纯电动汽车高速工况仿真车速Fig.8 Simulation speed of pure electric vehicle under high speed conditions

图9 纯电动汽车中低速工况仿真车速Fig.9 Simulation speed of pure electric vehicle under medium and low speed conditions

图8表明,使用双模糊控制器车型在CYC_HWFE高速工况运行过程中加、减速均表现平缓。在车辆仿真过程中为了便于更好地评价动力性，增加了加速测试模块和爬坡模块，结果显示最高车速达到149.2 km/h，在0～96.6 km/h区间内加速时间11.5 s，以88.5 km/h速度可以行驶在坡度为8%的路面上。图9表明，使用双模糊控制器车型在CYC_EUDC中低速工况下可实现较好的车速跟随循环工况行驶，平均车速为32.1 km/h，最大车速达到120 km/h，最大加速度为1.1 m/s2。

图10 纯电动汽车高速工况仿真电池SOCFig.10 SOC simulation of pure electric vehicle batteries under high speed conditions

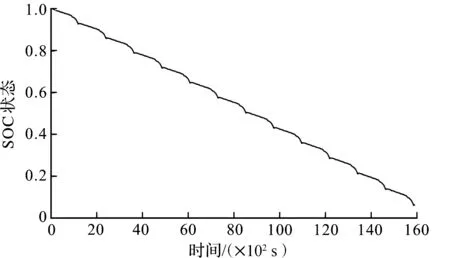
图11 纯电动汽车中低速工况仿真电池SOCFig.11 SOC simulation of pure electric vehicle batteries under medium and low speed conditions

图10仿真结果表明，使用双模糊控制器的车辆在高速驾驶工况中电池电量消耗较为平缓，运行结束后电池SOC状态大约为74%，控制效果较佳。其中，当车辆运行至5 min时，由于车速短时间内提升近一倍，致使电机输出功率急速升高，因此SOC状态出现了短暂的较大波动，后随车速逐渐稳定SOC下降趋势也趋于平稳。图11中在完成13次典型中低速循环工况仿真后，SOC状态从接近100%降到几乎为零，表明该车型使用双模糊控制器后续驶里程可达150 km以上，具有较好的动力性和经济性。

5 结 语

纯电动汽车驱动系统的性能会对车辆整体性能产生重要影响。在建立纯电动汽车动力学模型和输入参数模型后，利用设计的双模糊控制器求解车辆在某一信号输入状态下的期望输出转矩，并将转矩指令输出到电机控制器执行，基于ADVISOR平台搭建嵌入双模糊控制器的电动车模型，对其进行动力性与经济性仿真试验。结果表明，搭载双模糊控制器的纯电动汽车模型在保证动力性的同时，电池电量消耗较为平缓，且剩余电量相对较多，这为后续开发整车控制器综合控制策略奠定了良好的开发环境和试验基础。