相邻隧道围岩爆破振动影响规律研究

罗 阳，韦 麟，支彦锋，斯纪平，嵇晓晔，杨建辉

(1.浙江科技学院 土木与建筑工程学院，杭州 310023；2.浙江交工路桥建设有限公司，杭州 310051)

目前中国公路隧道的施工方法以钻爆法为主，隧道掘进施工产生的爆破振动效应有可能引起围岩的失稳、混凝土的开裂或脱落[1]。随着社会经济的急速发展，大量的公路复线隧道需要开挖施工，因此，研究减少或避免隧道掌子面爆破掘进施工对相邻已有隧道的爆破振动影响有现实意义。

李飞等[2]应用有限差分法FLAC3D程序动态模拟了隧道在不同围岩特性条件下装药量大小对相邻洞室围岩关键点的影响程度，提出了确保工程稳定的合理装药量。张仁根等[3]采用ABAQUS软件对相邻隧道在小净距隧道开挖时产生的爆破振动影响进行研究，提出将后行隧道爆破开挖时先行洞产生的塑性变形范围大小作为隧道净距合理与否评判依据，提出塑性区贯通两隧道间围岩时则认为隧道净距选取不合理或应采取相应措施。程康等[4]对多种爆破振速经验公式进行适用性分析，归纳了萨道夫斯基经验公式的爆破适用条件，提出了深孔爆破振速计算公式。刘国华等[5]基于爆破动力分析得出了在隧道形状、岩性以及初始应力状态不同时，结构不同部位的动态响应有较大的差别。叶培旭等[6]通过实时监测近距离交叉隧洞爆破施工对既有隧道的振动影响，研究了迎爆面位置、震源距离、围岩性质和最大装药量等对隧道振动速度的影响，提出了交叉隧道振速的控制方法。曹正龙等[7]利用爆破振速衰减规律，利用FLAC3D动力模型验证了在掏槽区打空孔和在拱顶取芯设置隔离带两种方案控制爆破振动影响的可行性。Butt等[8]研究了爆破振动频率对隧道结构的影响，认为振动安全判据需结合振动频率加以考虑。总体而言，目前国内外主要以爆破振动速度作为爆破振动安全判据，对爆破振动监测研究主要依靠爆破经验衰减公式。其中后行隧道掌子面爆破对先行隧道的爆破振动影响主要考虑小净距隧道、单段装药量及围岩等级，涉及隧道净距和车辆联络通道对邻近隧道围岩爆破振动影响的研究相对匮乏。依托工程现场，通过工程爆破振动监测数据和数值模拟相结合的方式，对相邻隧道间净距、联络通道距后行隧道掌子面距离、联络通道与隧道掘进方向所呈夹角对相邻先行隧道产生的爆破振动影响规律进行研究，以便为其他相似施工提供一定的参考。

1 爆破振动理论分析

炸药在岩体中爆炸后产生爆轰波和爆炸气体，同时压缩炮孔内空气产生高温和高压环境，对周围岩体产生高强度的拉伸和压缩等一系列复杂作用[9-10]。在此过程中岩体发生损伤、破碎和抛掷现象，同时产生地震波向四周进行传播。爆轰产物对岩体产生的直接冲击和抛掷范围有限，地震波的影响可传播很远的距离[11-13]。炸药爆破时，岩体受其扰动会引起质点相对于其平衡位置的循环往复振动，并将振动以一定速度传递至相邻质点，在此过程中，由于界面效应、介质不均及介质吸收等因素，导致能量不断耗散，质点的振动速度、振动频率和振动幅值都逐渐减小[14-15]。

2 数值计算模型合理性分析

结合舟山竹尖岗隧道工程实际，相邻隧道间净距为30 m，左侧隧道为先行隧道，右侧隧道为后行隧道。分别对无联络通道隧道和有联络通道隧道的先行隧道围岩进行爆破振动监测。其中联络通道与后行隧道掌子面相距30 m，与隧道掘进方向夹角为60°。爆炸中心位于后行隧道掌子面，起爆段位分别为1、3、5、7、9、11、13、15段，其中单段炸药最大量为41.6 kg，位于11段。爆炸中心同一横截面先行隧道右侧拱腰处围岩距离爆炸中心最近，该处围岩受爆破振动影响最大，在该点布置振动测点，如图1所示，并将此横截面定义为危险截面。

图1 振动测点布置Fig.1 Arrangement of vibrating measuring points

利用数值模拟软件ANSYS/LS-DYNA对模型进行计算分析，分析后行隧道掌子面最大装药量段位炸药爆炸时隧道净距和联络通道对先行隧道的振动影响作用。模型采用cm-g-μs单位；采用ALE流固耦合算法[16-17]；岩体材料选择凝灰岩，岩石密度为2.6 g/cm3，弹性模量为20 GPa，泊松比为0.2，抗压强度为120 MPa，剪切模量为8.33 GPa。炸药采用2号岩石乳化炸药，炸药爆破方程采用JWL本构方程[18]，炸药密度为1.3 g/cm3，爆压为0.32 GPa，爆速为0.55 cm/μs。采用Pro/Engineer软件建立与工程实际相同的两个隧道爆破模型，围岩宽80 m，高35 m，长150 m，隧道间按模型中线对称布置，净距取30 m。先行隧道布置于模型左侧，完全贯通围岩；后行隧道布置于模型右侧，开挖长度为100 m。模型采用耦合装药结构，沿右侧隧道掌子面中线对称布置6个截面尺寸为10 cm×10 cm的炮孔，隧道截面尺寸与炮孔布置如图2所示，1～6#炮孔装药量分别为8、6、6、7.2、7.2、7.2 kg。模型采用Hypermesh软件对隧道爆破模型进行网格划分。

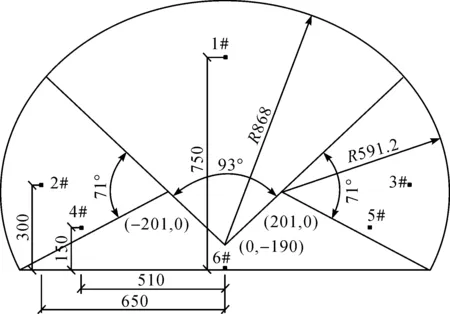
图2 隧道截面尺寸及炮孔布置示意(单位：cm)Fig.2 Tunnel section size and blast-hole arrangement (unit: cm)

图3 代表质点位置示意Fig.3 Location sketch of representative particle

为保证数值计算模型参数选取的合理性，将模型中与现场实际测点位置相对应的质点振速数据与实测数据进行对比分析，代表质点位置如图3所示。

图4、图5分别为质点x轴振速-时间曲线和质点振速-时间曲线。由图4～5可知，当相邻后行隧道掌子面炸药起爆后，代表质点在无联络通道模型中的最大x轴振速和最大振速分别为1.229、1.837 cm/s，与现场测点实测最大x轴振速和最大振速1.214、1.781 cm/s相接近；代表质点在有联络通道模型中的最大x轴振速和最大振速分别为2.248、3.132 cm/s，与现场测点实测最大x轴振速和最大振速1.910、3.226 cm/s相接近。因此该数值计算模型的参数设置比较合理，可进一步进行模拟研究。

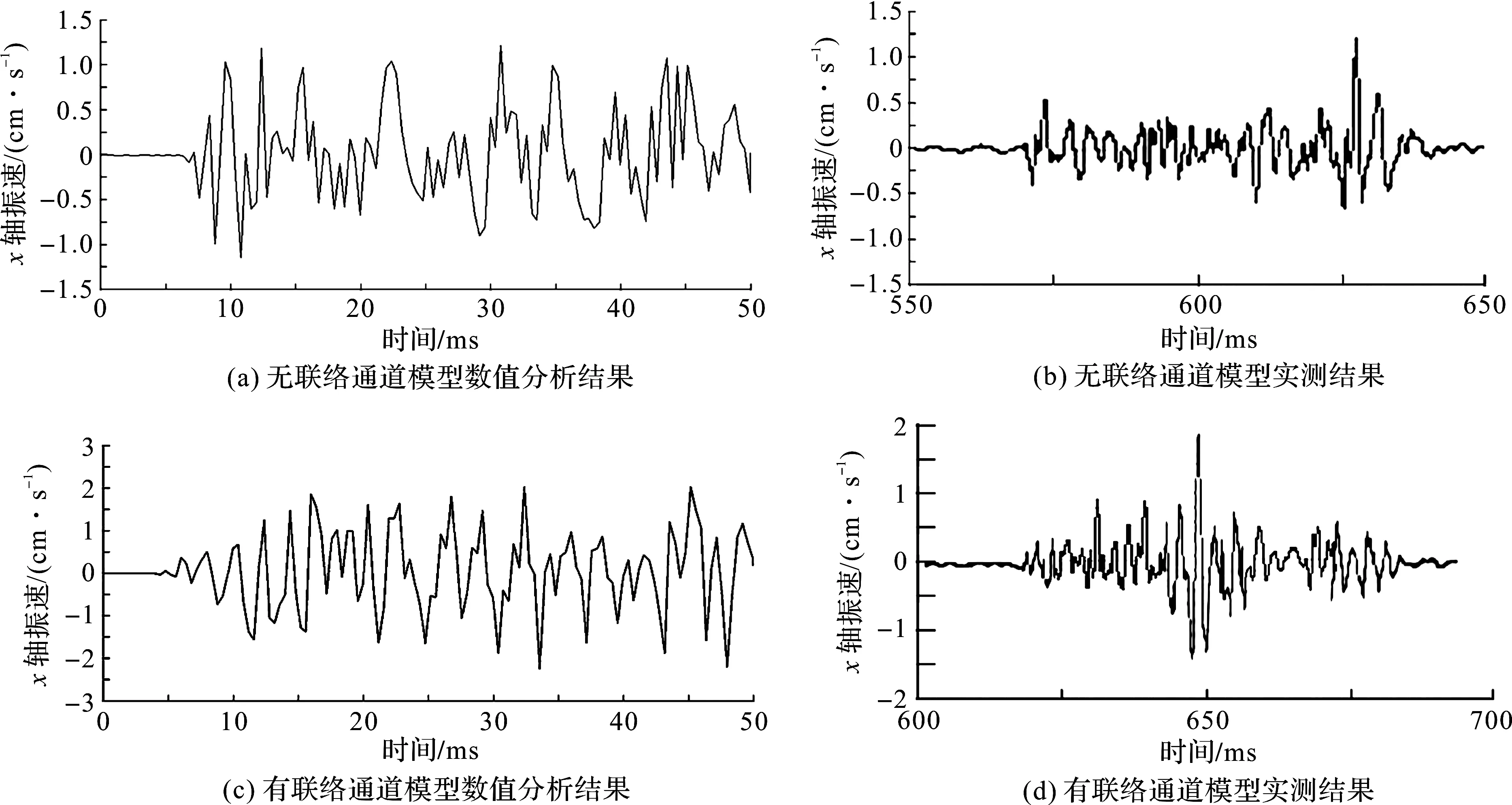
图4 质点x轴振速-时间曲线Fig.4 X-axis vibration velocity-time curve of particles

图5 质点振速-时间曲线Fig.5 Vibration velocity-time curve of particles

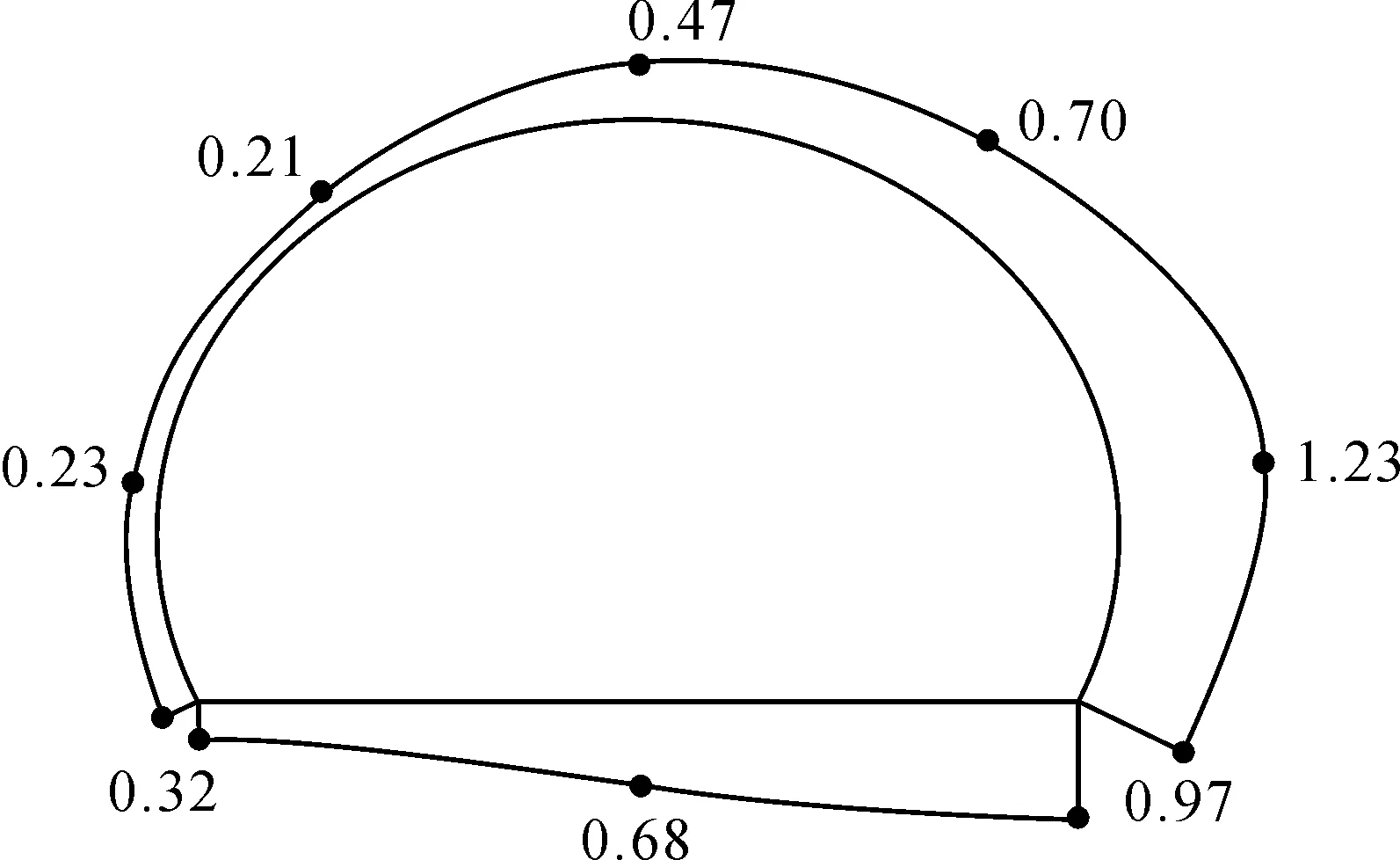
图6 危险截面最大x轴振速分布Fig.6 Maximum x-axis vibration velocity distribution of dangerous section

在模型中选取位于危险截面的8个代表性质点进行分析，得到最大x轴振速在危险截面上分布规律，如图6所示。由图6可知，先行隧道迎爆面质点最大x轴振速大于背爆面质点最大x轴振速，拱底最大x轴振速大于拱顶最大x轴振速。危险截面最大x轴振速曲线峰值位于迎爆面拱腰处，故认为该质点为后行隧道最危险质点。

3 无联络通道隧道爆破振动数值模拟

建立5个无联络通道几何模型，隧道间净距分别为10、20、30、40、50 m。对上述位于危险截面的8个质点进行分析，绘制隧道间净距不同时危险截面最大x轴振速曲线，如图7所示。由图7可知，先行隧道最危险质点均位于危险截面迎爆面拱腰处。

选取每个模型危险截面最大x轴振速曲线的峰值，绘制峰值与隧道间净距的关系曲线，如图8所示。由图8可知，随着相邻隧道净距的不断增大，最大x轴振速曲线的峰值不断减小，当相邻隧道净距超过40 m后，峰值减小趋势趋于稳定，因此后行隧道掌子面爆破对先行隧道的爆破振动影响可忽略不计，此时隧道间净距近似为隧道洞径的2.5倍。

图7 不同净距模型危险截面最大x轴振速分布Fig.7 Maximum x-axis vibration velocity distribution of dangerous sections with different clearances models

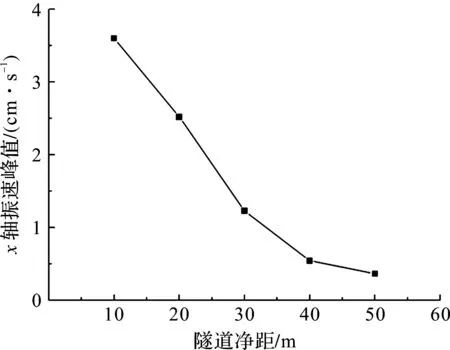
图8 x轴振速峰值与隧道净距关系曲线Fig.8 Relationship between maximum x-axis vibration velocity peak and tunnel clearance

将隧道开挖方向定义为正，绘制隧道间净距为10、30 m模型在+10 m截面、危险截面和-10 m截面处最大x轴振速分布曲线，如图9所示。由图9可知，当隧道间净距为10 m时，由于两隧道间净距过小，后行隧道掌子面对围岩中质点振动传递路径影响较大，+10 m截面处最大x轴振速均大于-10 m截面。当隧道间净距为30 m时，后行隧道掌子面对围岩中质点振动传递路径影响可忽略不计，+10 m截面处最大x轴振速与-10 m截面最大x轴振速基本上一致。

4 有联络通道隧道爆破振动数值模拟

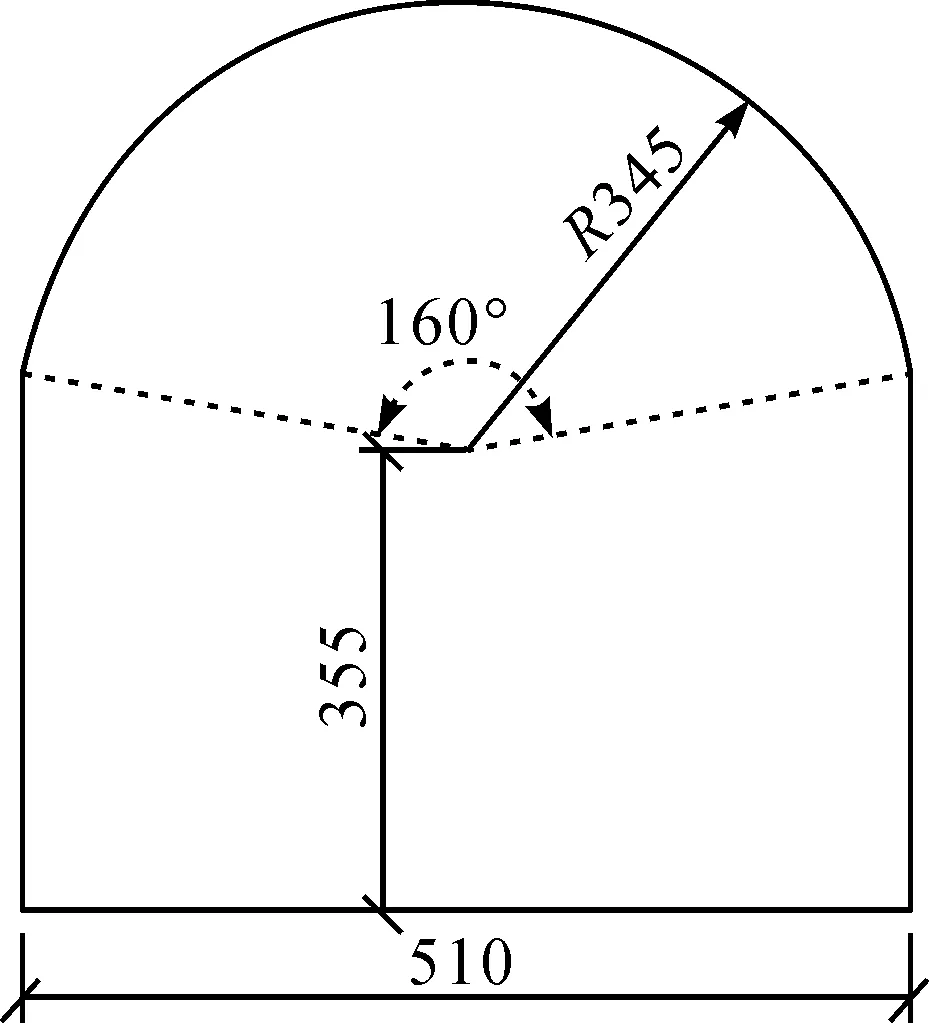
图10 联络通道截面尺寸(单位：cm)Fig.10 Liaison channel section size (unit: cm)

相邻隧道间联络通道破坏了隧道间岩体连续性，改变了隧道的整体结构，导致相邻隧道在此条件下所受的爆破振动影响产生变化，为此建立带有联络通道的相邻隧道模型进行爆破振动分析。隧道模型尺寸与无联络通道模型一致，在相邻隧道间创建一个车辆联络通道。联络通道截面尺寸如图10所示。

4.1 联络通道与掌子面不同距离数值模拟

建立6个数值分析模型，其中相邻隧道间净距为30 m，且以无联络通道几何隧道模型为参照，其他5个模型均设置联络通道，联络通道与隧道掘进方向夹角均为60°，几何模型示意如图11所示，联络通道与掌子面距离L分别为30、40、50、60、70 m。

选取每个模型危险截面最大x轴振速曲线的峰值，绘制峰值与L的关系曲线，如图12所示。由图12可知，危险截面最大x轴振速曲线的峰值随L的增大而不断减小，当L为70 m时，其危险截面最大x轴振速曲线的峰值为1.380 cm/s，与无联络通道下危险截面最大x轴振速曲线的峰值1.229 cm/s接近，此时，联络通道对先行隧道围岩爆破振动影响可忽略不计，L近似于隧道洞径的5倍。

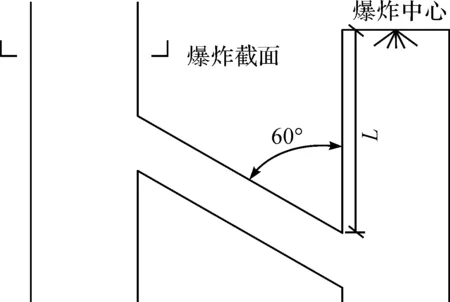
图11 模型几何尺寸示意Fig.11 Schematic diagram of geometry model

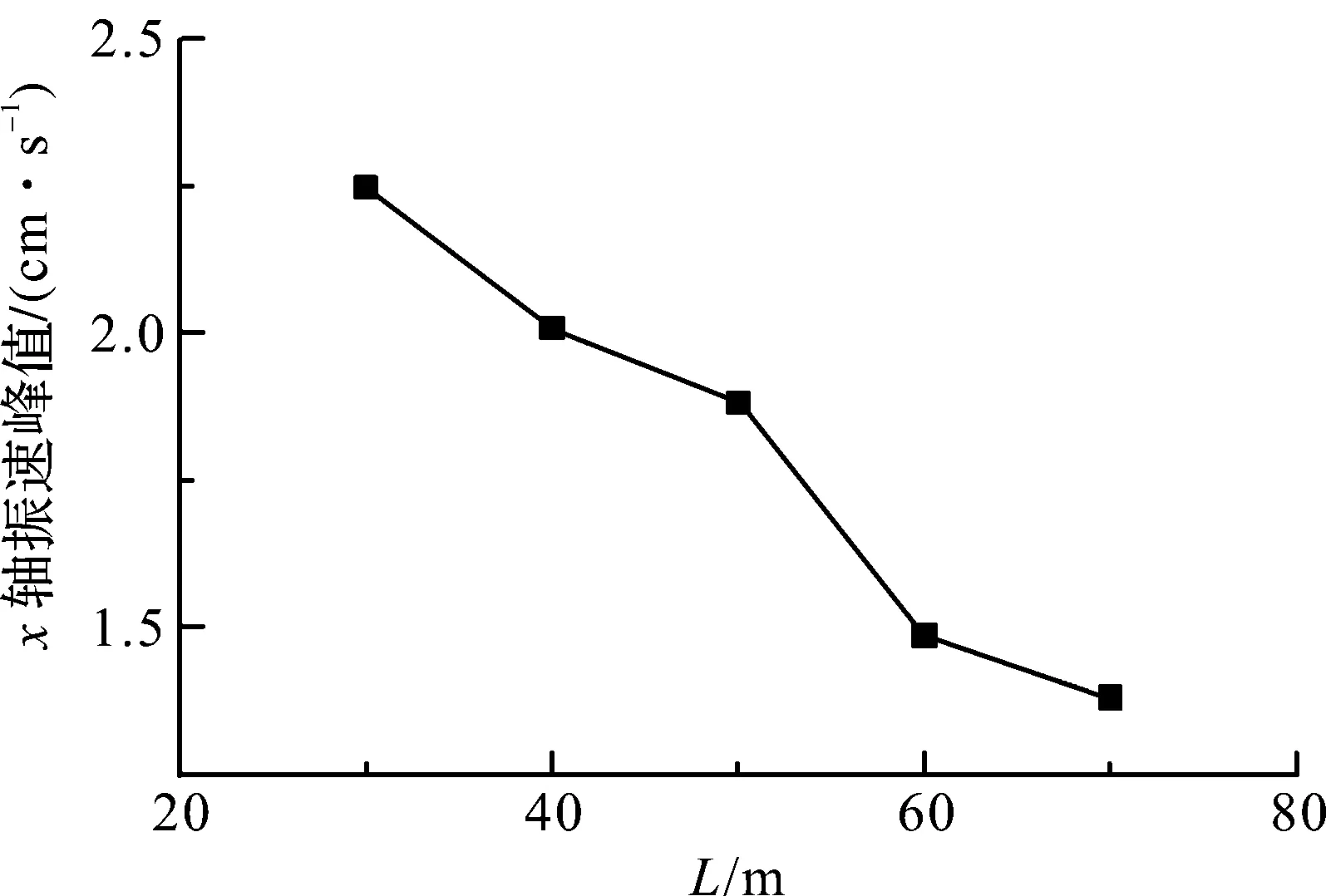
图12 x轴最大振速与联络通道位置关系曲线Fig.12 Relationship between maximum x-axis vibration velocity peak and position of liaison channel

4.2 联络通道与隧道不同夹角数值模拟

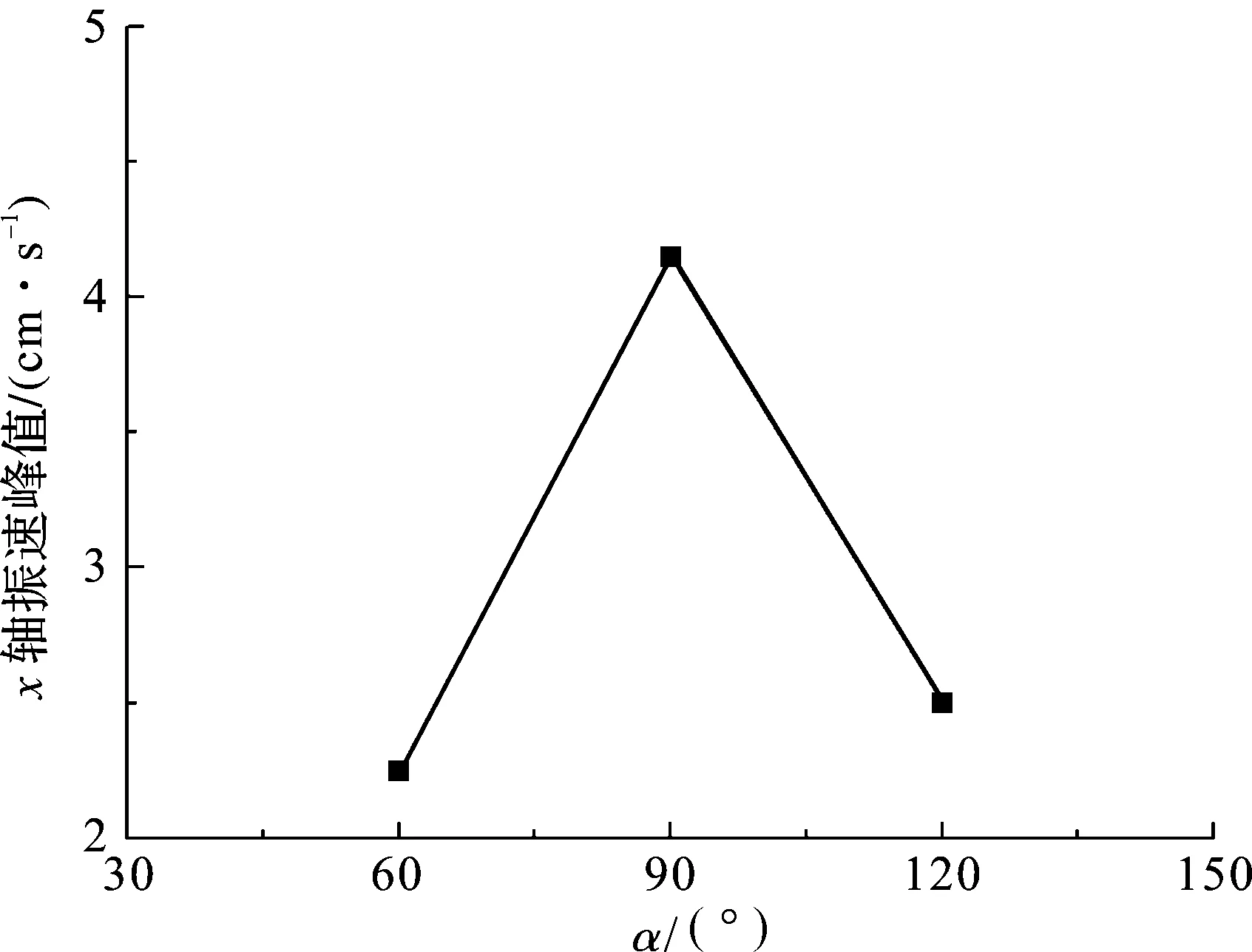
图13 x轴振速峰值与联络通道角度关系曲线Fig.13 Relationship between maximum x-axis vibration velocity peak and angle of liaison channel

在联络通道与后行隧道掌子面距离确定为30 m的前提下，建立3个数值计算分析模型，联络通道与隧道夹角α分别呈60°、90°、120°。

选取每个模型危险截面最大x轴振速曲线的峰值，绘制峰值与α的关系曲线，如图13所示。由图13可知，当α为90°时，联络通道与掌子面平行，爆破振动波在该断面下反射率最大，危险截面处最大x轴振速达到峰值。当两个断面与掌子面夹角相等时，两个断面的爆破振动波反射率相差不大，两者危险截面处最大x轴振速基本上一致。

5 结 论

采用ANSYS/LS-DYNA数值模拟软件进行相邻隧道后行隧道掌子面爆破对先行隧道围岩振动影响数值模拟，在炮孔尺寸为10 cm×10 cm，炸药采用密度为1.3 g/cm3的2号岩石乳化炸药，装药结构为耦合装药的条件下，得出以下结论：

1)质点距离爆炸中心越近，该点所受爆破振动影响越大。爆破施工时，相邻隧道同一截面处迎爆面围岩所受爆破振动影响大于背爆面所受影响；相邻隧道最危险截面位于爆破截面，最危险质点位于最危险截面迎爆面拱腰处。

2)相邻隧道同一截面上x轴最大振速随隧道净距的增大而减小，当隧道净距大于2.5倍隧道洞径时，可忽略爆破施工对相邻隧道围岩的爆破振动影响。

3)相邻隧道x轴最大振速随联络通道与掌子面距离L的增大而减小，当L大于5倍隧道洞径时，可忽略联络通道对相邻隧道围岩的爆破振动影响。

4)当联络通道垂直于隧道掘进方向时，相邻隧道围岩所受爆破振动影响最大，因此，应避免设计垂直于隧道掘进方向的联络通道。