基于频谱特征的淬硬层深度脉冲涡流检测仿真分析与试验

(重庆大学 机械工程学院，重庆400044)

随着现代技术的飞速发展，对各类金属工件的质量要求越来越高。对工件的表面硬化处理是提高工件性能的重要手段之一。表面硬化层深度是评判工件表面质量好坏的重要指标，所以测量工件表面硬化层深度非常重要。目前，可准确测量表面硬化层的方法大都属于破坏性的测量，并且是抽样检测，比如金相法、显微硬度法、化学酸蚀法等。而涡流检测方法不破坏工件，测量简单方便、结果准确，且属于非接触式测量。刘本田等[1]采用数值模型方法，导出了磁性材料的线圈阻抗增量解析式，并用试验验证了结果。程晓敏等[2]利用有限元方法对渗碳层深度的涡流检测方法进行了研究。王春艳等[3]采用单频涡流法与硬度试验法进行对比，结果表明涡流检测可作为一种可靠的测量淬硬层深度的方法且测量结果精度较高。CUFFE等采用多频涡流和脉冲涡流方法测量表面淬硬层深度，但其受外界干扰较大。

在目前的研究中，使用涡流方法测量表面淬硬层深度时，主要利用单频涡流提取检测信号峰值进行分析，获得信号峰值与淬硬层深度的函数关系，进而测量材料表面淬硬层深度。因为表面淬硬层与芯部组织的电磁特性相差不大，而检测信号由二次磁场感应产生，信号非常微弱，通常处于微伏到毫伏级，单从时域检测信号峰值来测量表面淬硬层深度时，容易受到外界干扰[4]。脉冲涡流检测是一种新的涡流检测方法，包含丰富的频率成分，可比传统的单频涡流检测提供更多的信息，克服了传统单频涡流检测深度不全面的问题[5]。笔者提出了基于频谱特征的淬硬层深度脉冲涡流检测方法，利用COMSOL软件建立了淬火工件的模型进行仿真，仿真结果表明，频率特征量淬硬层深度具有良好的线性关系。最后，对提出的特征量进行了验证试验。

1 淬硬层脉冲涡流检测原理

1.1 脉冲涡流原理

脉冲涡流激励信号为脉冲信号，探头中加载的电流或电压会感应出一个快速衰减的脉冲磁场，变化的磁场会在导体中感应出瞬时涡流。导体内的瞬时涡流又会产生瞬态磁场，进而在检测线圈或者磁传感器上感应出随时间变化的电压。根据电磁感应原理，脉冲涡流检测信号也包含相同频率成分的分量[6-7]。工件表面硬化层与芯部组织电导率、磁导率不同，而涡流对这些电磁特性非常敏感，所以工件内电磁特性的变化可以通过涡流检测信号反映出来。分析脉冲涡流检测信号，便可以建立淬硬层深度与检测信号之间的关系从而实现淬硬层深度的测量。

脉冲信号一般为周期方波信号。根据傅里叶级数展开，周期方波信号包含基波成分、各奇次谐波成分，如式(1)所示。

(1)

式中：A为周期方波信号的幅值；f为方波信号的频率;t为信号的持续时间。

典型的脉冲涡流时域检测信号与其幅频谱如图1所示。常规的脉冲涡流信号在时域中进行分析时，主要采用的特征值为峰值和峰值时间。

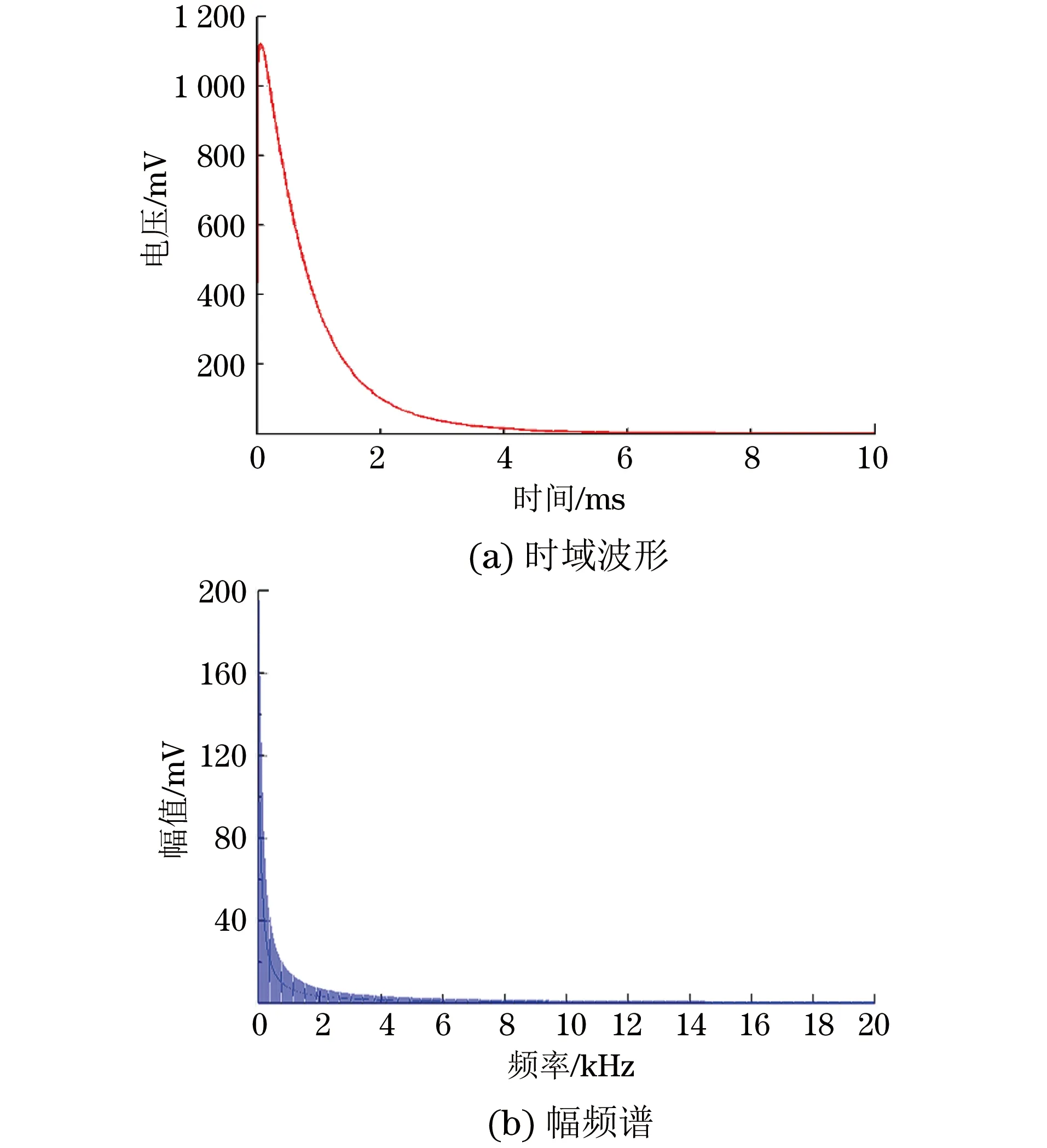
图1 典型脉冲涡流检测信号

1.2 趋肤深度

趋肤深度为涡流标准渗透深度，其定义为

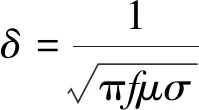
(2)

式中：f为激励信号频率，Hz;μ为材料的磁导率,H·m-1；σ为材料的电导率，S·m-1。

由式(2)可以看出，频率越高、导电性能越好或导磁性能越好的材料，趋肤效应越明显。

脉冲信号包含的频率范围广，不同的频率渗透深度不同，若找到刚好渗透到淬硬层与芯部组织分界面处的频率，则可测量出淬硬层深度。

1.3 基于频谱的淬硬层深度测量原理

工件进行感应淬火之后，表层组织转变为马氏体组织，芯部仍为原始组织，即铁素体组织，表层与芯部之间有过渡层。表层组织碳含量大于芯部组织的。一般情况下，碳含量的增加会导致材料磁导率、饱和磁感应强度等参数的降低，而电导率会增加。因此，通过工件表面淬硬层与芯部组织的不同电磁特性，可以确定表面淬硬层的深度。

因为工件表层与芯部的磁导率、电导率不同，所以在表层与芯部产生的涡流信号也就不同。首先检测参考工件，即工件的材料组织全为马氏体组织，将在此工件上获得的时域检测信号作为参考信号x0(t)，然后分别获得待测工件的时域检测信号xi(t)。对获得的检测信号进行傅里叶变换，如式(3)所示，然后对谱信号进行差分，如式(4)所示。

x0(t)⟺X0(f)xi(t)⟺Xi(f)

(3)

式中:X0(f)为参考信号幅频谱;Xi(f)为工件的检测信号幅频谱。

Di(f)=Xi(f)-X0(f)

(4)

式中：Di(f)为差分幅频谱信号。

因为待测工件与参考工件在有表面淬硬层的地方所感应出的涡流是相同的，检测线圈感应到的信号也相同，即幅频谱信号中感应涡流处于表面淬硬层的频段幅值相同。令

Di(f)=0

(5)

求解出第一个过零点频率f0，建立该特征频率与淬硬层深度的关系，从而检测出淬硬层深度。该特征量是根据涡流趋肤深度原理获得的，由式(2)可知频率的开方与趋肤深度成反比，因此建立如式(6)所示的关系。

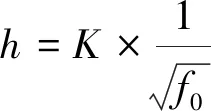
(6)

式中：h为淬硬层深度，mm；K为系数；f0为差分幅频谱信号中过零点的频率，Hz。

获得不同材料的K值，检测出材料脉冲涡流幅频谱信号中的过零点频率，即可通过式(6)实现不同材料淬硬层深度的测量。

2 脉冲涡流检测仿真模型的建立

笔者选择COMSOL有限元分析软件进行建模及分析。COMSOL软件进行瞬态电磁场仿真时是基于麦克斯韦方程组进行求解的，麦克斯韦方程组微分形式如式(7)～(9)所示。

(7)

B=×A

(8)

H=μ-1B

(9)

式中:A为磁矢势；B为磁感应强度;H为磁场强度;J为电流密度。

对瞬态电磁场的仿真即为解电磁场方程，如式(10)所示。式(10)为麦克斯韦方程组组合而得。

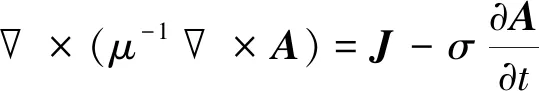
(10)

涡流检测中涡流探头、工作频率等对检测结果的影响较大，灵敏度越高的探头检测效果越好。文中选择圆柱形线圈作为淬硬层深度测量的激励和检测线圈[8]。建立的仿真模型如图2所示。激励线圈为圆柱形，高度为45 mm，内径为45 mm，厚度为2 mm，匝数为500匝，漆包线线径为0.35 mm；检测线圈也为圆柱形，高度为10 mm，内径为10 mm，厚度为2 mm，匝数为1 000匝，漆包线线径为0.1 mm；线圈提离距离均为1 mm；被测工件为一个大平板，尺寸(长×宽×厚)为200 mm×200 mm×8 mm，由于过渡层很薄，文中先不考虑过渡层的影响，而模拟淬火件的表面淬硬层与芯部组织这两部分，建立一个两层的结构模型，如图3所示。淬硬层的电导率为σ1，相对磁导率为μr1，芯部组织的电导率为σ2，相对磁导率为μr2。由于两者电导率差别非常微小，故认为σ1=σ2。因为一般情况下激励电流密度是小于106A·m-2的，即相当于对材料进行弱技术磁化，故可以利用材料的初始磁导率进行仿真计算，文章采用20Cr淬火钢进行分析。对淬火件剖分测得表面淬硬层的初始相对磁导率μr1=66.53，芯部组织的初始相对磁导率μr2=88.17[1]。查《热处理手册》中的第四卷(第四版)可得20Cr在20 ℃下的电导率σ1=σ2=5.3×106S·m-1[9]。脉冲激励的方波电压为10 V，频率为50 Hz，占空比为0.5，由趋肤深

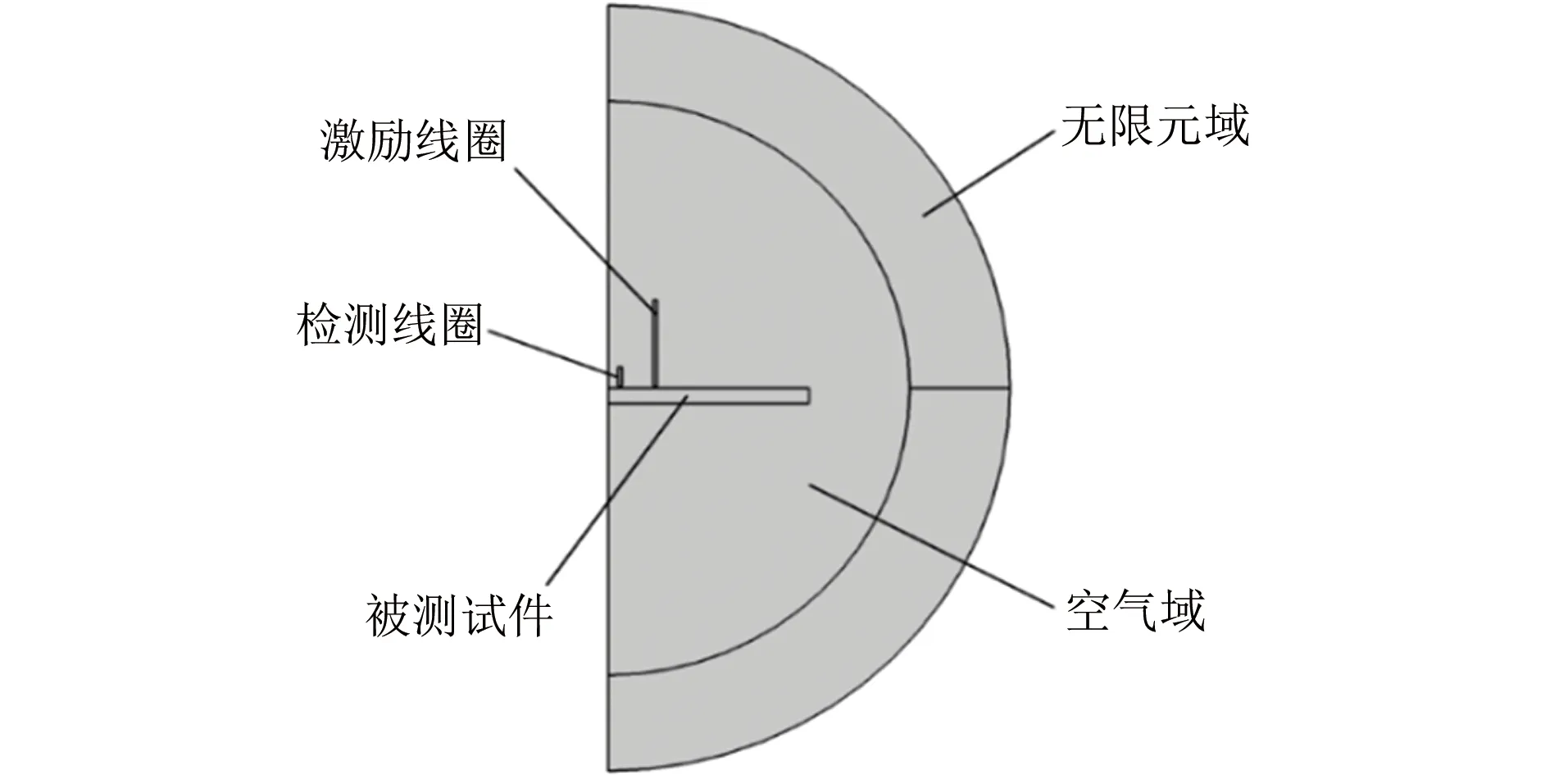
图2 建立的仿真模型

度公式可得趋肤深度为3.3 mm。为了使测量结果准确，趋肤深度应大于表面淬硬层深度。取工件理论淬硬层深度分别为0.8，1.0，1.2，1.4，1.6，1.8，2.0，2.2 mm。

3 仿真结果分析

3.1 时域检测信号

对不同淬硬层深度的工件进行仿真，得到的时域信号如图4所示。由图4可以看出，各不同淬硬层深度的信号几乎重叠，直接观察其时域原始检测信号几乎不可能。不同深度的感应电压与参考信号的差分信号变化最大也只有几个毫伏，相对于信号峰值来说非常微小。通过提取差分信号峰值与峰值时间，可以拟合出峰值与淬硬层深度的关系表达式，从而计算出表面淬硬层深度，用这种方法测量的精度也很高，但是其易受外界干扰而得到不准确的测量结果。

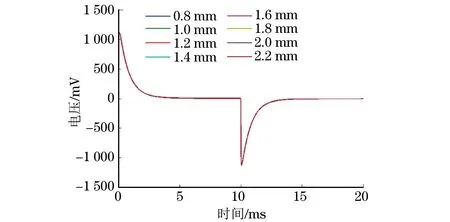
图4 不同淬硬层深度工件的时域检测仿真信号

3.2 频谱差分信号的淬硬层深度确定

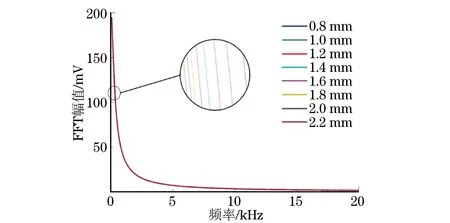
图5 不同淬硬层深度工件检测信号的幅频谱(仿真)

文章考虑从频域信号来准确测量淬硬层深度。对检测信号进行傅里叶变换(FFT)，得到如图5所示的幅频谱包络图。因为不同淬硬层深度的时域检测信号变化很小，所以检测信号频谱图的变化也十分微小，直接通过观察频谱图来获得淬硬层深度的难度也很大。从图5的局部放大图中可以看出，各淬硬层深度的频谱幅值随着淬硬层深度的增加呈递减趋势，但是单纯从幅值递减不能计算出淬硬层的具体深度，幅值的降低与淬硬层深度并非成函数关系。为了将频谱信号明显区分开来，考虑从频谱差分信号特征量来计算表面淬硬层的深度。

幅频谱差分信号如图6所示，幅频谱差分信号是用各不同淬硬层深度待测工件的检测信号频谱减去参考信号频谱得到的。从图6可以看出，各检测信号在高频部分几乎没有区别，仅在低频部分，即在待测工件表面的区别明显。这是因为高频成分涡流趋肤深度浅，集中在工件表面淬硬层，与参考工件产生的涡流信号一致，检测线圈检测到的信号也就一致。图7为差分频谱信号的低频部分局部放大图，可以看出：差分信号呈指数下降，且淬硬层深度越深，下降得越快；过零点频率随着淬硬层深度的增加而降低。故，基于上文所述的测量原理即可实现对表面淬硬层深度的定量测量。

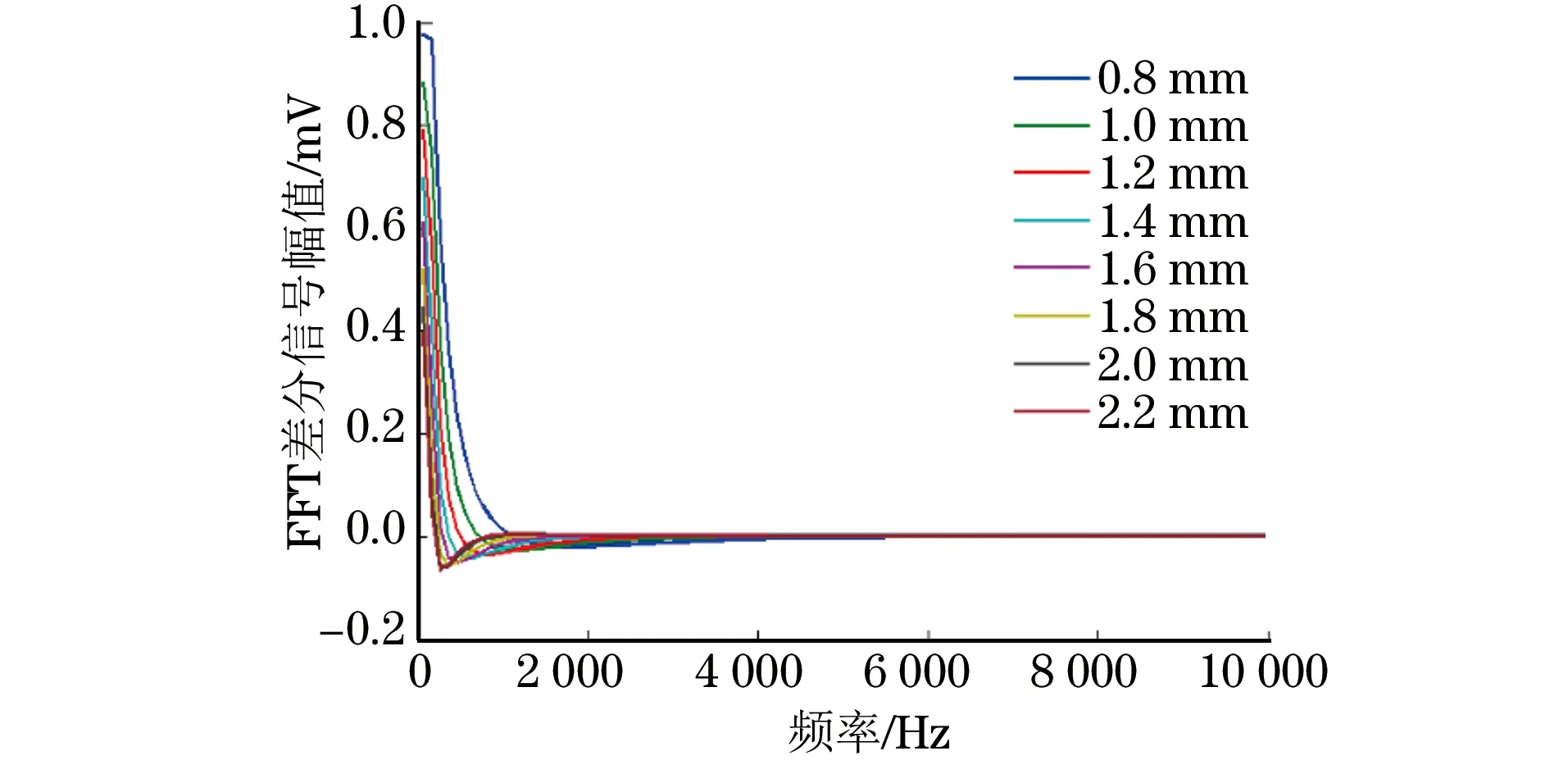
图6 不同淬硬层深度工件的幅频谱差分信号(仿真)

图7 不同淬硬层深度工件的频谱差分信号的 低频部分局部放大

利用三点样条插值法提取差分信号过零点作为特征值，根据式(6)可得表1。

表1 不同淬硬层深度K值计算结果

由表1可得，K值的平均值=26.61。特征频率随着淬硬层深度的增加而降低，这与频率越高，趋肤深度越浅是相对应的。利用式(6)来反向计算工件的表面淬硬层深度，可得表2与图8(图中工件编号1～8依次对应淬硬层深度为0.8～2.2 mm的工件)。

表2 不同淬硬层理论深度与计算深度的对比

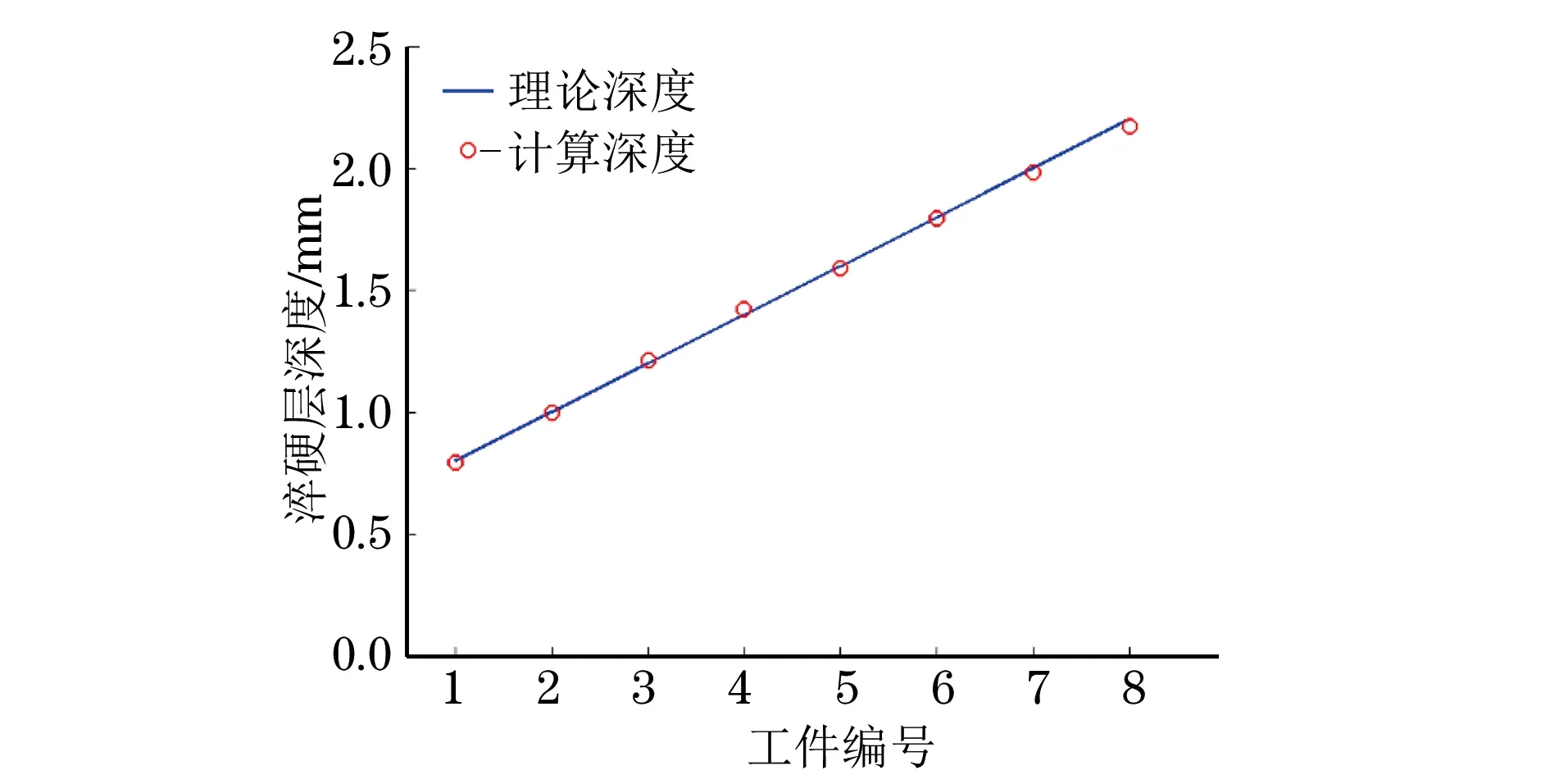
图8 工件的淬硬层深度计算值与理论值比较

由表2与图8可以看出，淬硬层深度的理论值和计算值非常接近，平均相对误差小于1%，这验证了使用该方法测量淬硬层深度的准确性及可行性。

4 试验系统及结果分析

4.1 脉冲涡流检测系统

脉冲涡流检测系统由信号发生器、功率放大器、线圈、数据采集模块等组成，检测系统框图如图9所示。

图9 脉冲涡流检测系统框图

采用FeelTech FY3200S型信号发生器产生脉冲方波激励信号，方波电压信号幅值为4 V，频率为50 Hz，占空比为0.5。采用FPA1016型功率放大模块将产生的方波信号进行功率放大。采用NI公司生产的CompactDAQ-9188数据采集卡进行数据采集，采样频率为100 kHz。

激励线圈采用线径为0.2 mm的漆包线绕400匝制成，内径为5 mm，高为16 mm。检测线圈内径为2 mm，高为4 mm，用线径为0.05 mm的漆包线绕500匝制成。

为了模拟不同感应淬火表面淬硬层深度，准备了3个不同淬硬层深度(分别为1.12，1.56，2.18 mm)的待测工件，工件材料为40Cr，采用金相法对淬硬层深度进行测量。

4.2 试验结果分析

利用检测系统对待测工件以及参考工件进行了检测，得到不同淬硬层深度的时域检测信号，其中参考工件脉冲涡流检测时域检测信号如图10所示。

图10 参考工件的时域检测信号

待测工件时域检测信号为5个周期，将5个周期叠加后平均得到一个周期的时域检测信号。利用一个周期的时域检测信号进行频谱分析，将测得的时域信号进行傅里叶变换,按上文所述的方法进行分析，得到频谱差分信号，如图11所示。

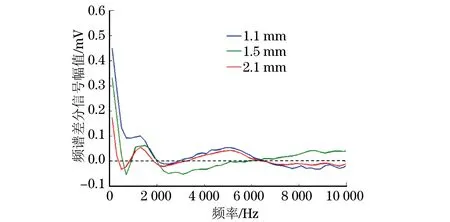
图11 待测工件的幅频谱差分信号

从图11可以得到差分信号过零点，根据式(6)得到如表3所示数据。

从图11可以看出，频谱差分信号过零点与仿真结果一致，特征频率随着淬硬层深度的增加逐渐减小，验证了该理论的可行性。

从表3可以看出，计算深度与实际深度的相对误差在可接受范围内，产生误差的原因主要有：

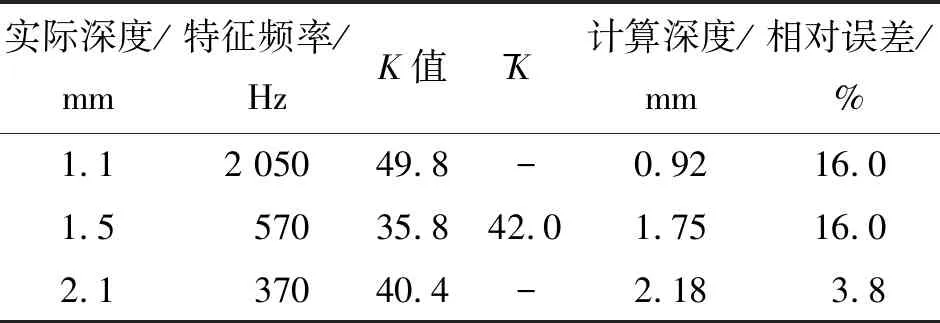
表3 工件淬硬层实际深度与计算深度的对比

(1) 测试过程中线圈与待测工件之间的位置很容易发生变化，检测结果受提离效应影响较大。

(2) 受外界磁场的干扰和噪声的影响较大。

(3) 脉冲涡流检测试验系统中的仪器精度不够，致使产生的激励信号不稳定。

5 结论

提出了用于淬硬层深度检测的新特征量——频率，利用COMSOL软件进行了建模与仿真分析，并对理论结果进行了试验验证，得出如下结论。

(1) 在时域方面检测信号的差别微小，易受外界噪声的干扰。

(2) 在频域方面，对理论提出的新特征量进行了验证。仿真结果表明，过零点频率随着淬硬层深度的增加而减小，使用该特征量计算出的淬硬层深度与实际深度的平均相对误差小于1%。

(3) 验证试验结果与仿真结果保持一致，表明使用频率特征量计算淬硬层深度具有可行性。