基于二次修正的短时行程时间预测模型

杨 航，王忠宇，邹亚杰，吴 兵

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.上海海事大学 交通运输学院，上海 201306)

短时行程时间预测是智能交通系统的基础输入之一，也是道路交通运行状态的重要评价指标[1].一般认为，两个决策点之间的时间跨度小于或等于15 min属于短时预测[2].高速公路行程时间的预测方法主要有时间序列法[3]、卡尔曼滤波模型[4]、支持向量机模型[5]、神经网络模型[6]、数据挖掘法[7]以及一系列组合模型[8]等.在近几年的研究中，由于组合模型可以克服单一模型在预测时的缺陷，通常呈现出优于单一模型的预测精度[9]，因此组合模型出现的频率逐渐提高.Zhang等[10]指出,交通流特征由两部分组成：一是确定性特征，影响因素为道路几何设计、常态下的交通需求、交通管理措施(限速)等；二是非确定性特征，影响因素为交通事件、恶劣天气等突发因素.因此，高速公路行程时间不仅包含确定性的周期性特征，还存在非确定性的残余成分[11].

周期性分析是行程时间预测中极其重要的一部分，现有研究已经证明行程时间在时间上和空间上均存在着较为显著的周期性.Zhang等[12]提出行程时间的周期性特征表现为以下两种：一种是以一天24 h为比较维度，一种是以一周7 d为比较维度.两种维度下相同路段的行程时间多数呈现较为明显的周期性特征.Zou等[13]采用了基于三角函数成分的回归模型对行程时间的周期性进行了分析，并证明该回归模型在预测间隔超过30 min时仍具有较好的预测精度.Zhang等[14]采用频率分析法对车辆在不同路段的周期性特征进行了提取和分析，并基于分析结果对车辆在不同货运点的延误时间进行了预测.

除去体现确定性成分的周期性特征，还需要对非确定性的残余成分进行分析，以提高预测精度.Vlahogianni等[15]指出，需要对行程时间数据进行去趋势化分析，以提升预测精度.去趋势化分析指的是将周期性预测值从原始数据中去除，对剩余不确定性的残量部分进行二次预测.现有研究主要采用多状态转换模型[16]进行去趋势化分析.马尔可夫链模型是去趋势化分析中较为有效和常见的一种手段，往往用于和其他模型配合使用以提高预测精度.D’Angelo等[17]采用马尔可夫链与周期性预测相结合的方式，对高速公路的常发性拥堵进行了预测，结果证明该模型比对照组模型有较为显著的预测优势.Yeon等[18]基于交通状态划分结果，建立了交通状态概率转移矩阵，构建了非连续的马尔可夫链模型，并比较了不同交通状态下各模型对高速公路各路段行程时间的预测精度.

基于二次训练的周期性预测和去趋势化分析的结合是当前大部分组合模型的组成结构，但Polson等[19]通过分析一次训练与二次训练的误差传递规律得出：基于多次训练的预测方法会造成过拟合的发生，降低模型在数据波动性较强情况下的预测精度.Zhang等[20]考虑了预测中数据的波动性因素，并采用频谱分析法提高了行程时间的预测可靠度.

现有研究的关注点多数聚焦在如何提升短时行程时间预测模型的预测精度，而对于不同交通状态下的预测稳定性、组合模型可能产生的多余噪声以及行程时间突变点(数值激增或骤降的时刻)的预测及时性等方面的内容涉及相对较少[21-22]，需要进一步考虑模型在这些方面的优化问题.

本研究改善了传统组合预测模型的结构，通过噪声修正模型构建了波动性分析模块，缓解了过拟合效应所带来的预测不稳定性.同时，面向相对误差修正的马尔可夫链不需要针对交通状态进行状态划分，提升了模型的应用灵活性，使得模型具备了处理其他高速公路路段行程时间数据的潜力.此外，噪声修正模块的加入提高了模型在拥堵状态下的预测精度和鲁棒性，使得模型具备了捕捉行程时间突变点的能力，缓解了预测的延迟性，从而可为高速公路交通运行管理提供决策依据.

1 数据来源和采集

本研究所使用的行程时间数据采集于美国高速公路US -290中的编号 I-610 至 FM-1960间的路段，位于德克萨斯州的城市休斯顿.数据采集时间段为2008年1月至2008年8月的每周二到四，每隔30 s采集一次，每30 s的检测数据集计成5 min的区间，一天共采集24 h.该路段有着较明显的潮汐特征，路段由东向西方向在晚高峰承担了大量交通流.这种交通流的不均衡性，有助于检验组合模型波动性分析模块的有效性，也有助于验证组合模型在捕捉晚高峰行程时间“拐点”的及时性和稳定性.研究路段长19.3 km，自由流速度下的通过时间约为15 min.路段上共布设了六个AVI (automatic vehicle identification) 检测器，在车辆通过时记录车牌号，通过相同车牌在各个检测器经过的时刻间隔获取行程时间.六个检测器将选定路段分为五个子路段(A、B、C、D、E)，长度分别为1.3、4.2、4.8、2.4、6.6 km.检测器布置如图1所示，虚线框包围部分为本研究所要涉及的路段，每个雷达感应器旁标注的四位数为对应编号.

2 组合预测模型

本研究的组合模型分为以下三部分：体现确定性特征的周期性部分，采用小波神经网络(WNN)预测原始数据，得到初步预测值；体现非确定性误差特征的残量部分，采用马尔可夫链(MKC)对初步预测值的相对误差进行修正，得到预测后的相对误差值；体现非确定性噪声的波动分析模块，采用GJR-GARCH (Glosten-Jagannathan-Runkle-generalized-autoregressive-conditional-heteroskedasticity)模型缓解噪声.最终的短时行程时间组合预测值为三部分预测值之和，组合预测模型WNN-MKC-GJR的结构表达式如下所示：

Xt=ct+rt+vt

(1)

式中：Xt为组合模型t时刻的预测值；ct为改进后的小波神经网络t时刻的周期性预测值；rt为经过马尔可夫链修正的t时刻的相对误差值；vt为GJR-GARCH模型预测的t时刻波动量.

2.1 小波神经网络模型

作为人工智能算法之一的神经网络可用于检测常态下交通流的周期性特征，并在预测行程时间周期性的实例中得到了成功应用[23].小波神经网络拓扑结构如图2所示.图2中,ui为第i个输入变量,wi为ui对应的输入层节点,Ti为ui对应的输出层节点,Y(ui)为ui对应的小波基函数.本研究的神经网络中，输入层为各个时刻的行程时间真实值，输出层为各个时刻对应的行程时间预测值，中间层为各个输入值对应的小波变换函数，因此各层的神经元数量相同.

图1 US-290路段

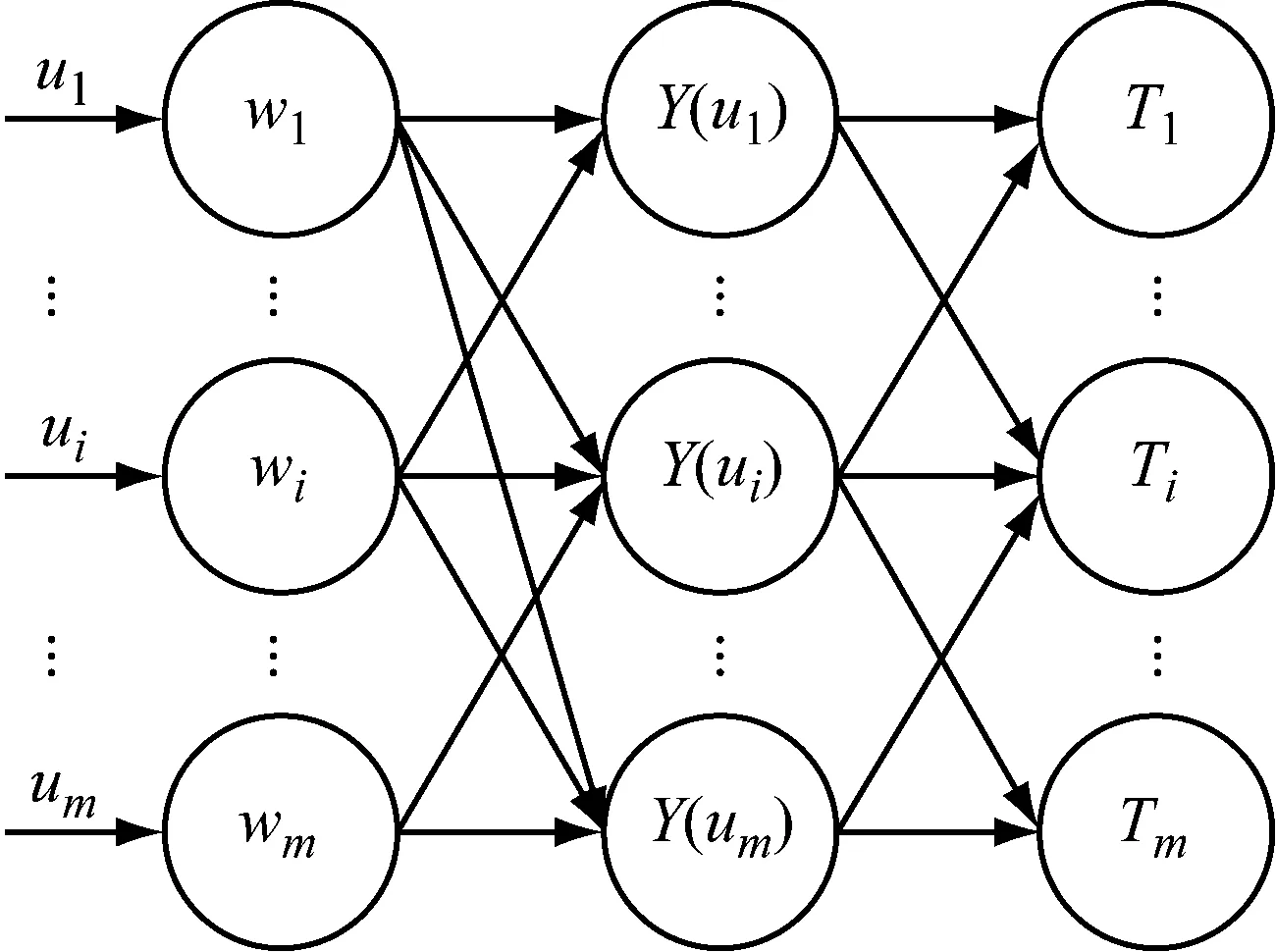
图2 小波神经网络的拓扑结构

采用母小波基函数作为隐藏层激发函数，该函数通过变换分析信号的局部特征，在捕捉原始数据的周期性特征上具有稳定性和高效性[24]，函数表达式为

(2)

小波神经网络的算法核心是小波分析和傅里叶变换，变换的频率和振幅决定了小波预测结果的振荡幅度.Antonini等[24]通过增加二次误差反馈模块，基于误差动态实现小波变换的频率和振幅，增加了小波变换的稳定性.动态小波变换函数yt和小波系数关系函数O(yt-1)如下所示:

yt=f(yt-1)+g(xt-1)+et

(3)

(4)

式中：x(t-1)为(t-1)时刻的状态向量；yt-1为(t-1)时刻反馈的行程时间输入向量；f(·)为关于yt-1的标量化非线性映射函数；g(·)为关于xt的标量化非线性映射函数；et为t时刻实际行程时间值与未来输出层预测值之间的误差向量；M为分析时段内出现的完整小波周期数；O(yt-1)为f(yt-1)的极大似然估计值；Wq为第q个周期的离散化小波变换系数；a为频率(振幅)；b为时空维度；L(yt-1)为小波变换函数yt-1的二维函数空间；ψa,b(yt-1)为二维小波衍生函数.ψa,b(yt-1)是基于标准化小波函数转化而来，如下所示：

(5)

式中：φ(·)为标准化小波函数.以这两个函数构成小波变换函数，对传统小波神经网络结构进行改进，减少需要标定的参数个数，提高算法的收敛速度.

2.2 马尔可夫链模型

Zhang[25]的研究指出，神经网络在t时刻的预测误差与(t-1)时刻是高度相关的，而与之前时刻的相关性很小.马尔可夫链模型的显著特征是非后效性，即目标在当前时刻的状态只与前一个时刻的状态相关，而与之前任何时刻的状态无关，与神经网络预测误差的特征相符合.现有研究多采用马尔可夫链对交通流运行状态进行划分，分为拥堵、半拥堵与非拥堵三个状态[18].该划分方法的缺点在于半拥堵的过渡状态很难量化，当过渡状态不明显时，会严重影响马尔可夫链的收敛精度及速度.针对误差的状态划分方法则具有更广泛的适用性.采用马尔可夫链对初步预测值的相对误差进行二次修正，获得的修正值将作为相对误差预测值.

多状态转换模型的预测过程包含以下三个步骤：确定各个状态及对应区间，将待处理数据放入对应区间，预测每个区间出现的概率.作为多状态转换模型的一种，马尔可夫链的构建及求解过程亦遵循这一过程.首先将小波神经网络训练组的相对误差集合成数据链，将相对误差划分为N个状态(s1,s2,…,sN)，每一个状态对应一个相对误差区间.采用一种基于二叉判定图的划分方法对数据链进行状态划分，关于该方法的细节可参考Xie等[26]的研究，每个状态对应一个相对误差的范围区间.接着，将数据链中的各个误差分入对应的区间.最后,在数据划分的基础上对相对误差的最终状态进行求解.

构建马尔可夫链一步转移概率矩阵P，矩阵中的每个元素为pIJ，表达式如下所示：

(6)

式中：pIJ为小波神经网络训练组的相对误差由第I个状态转移至第J个状态的出现概率；oI为第I个状态出现的次数；oIJ为第I个状态转移至第J个状态的次数.

定义系统的初始状态矩阵为S0，表达式如下所示：

(7)

经过K次一步转移概率矩阵运算后得到最终状态SK，SK可通过切普曼-柯尔莫哥洛夫方程求得，如下所示：

SK=SK-1P=S0PK

(8)

待马尔可夫链收敛之后，每个最大概率对应的状态被选为修正状态，对应的区间作为相对误差的修正区间，取每个时刻t的预测区间中值Ut作为相对误差值的预测值rt，表达式如下所示：

rt=dt(1-Ut)

(9)

式中：dt是经过AVI检测器获取的t时刻行程时间原始数据.

2.3 GJR-GARCH模型

将人工智能算法与统计学方法相结合的组合预测模型容易引入多余噪声，从而产生过拟合效应，这对于高峰时期波动性较大的行程时间的预测精度和预测稳定性带来很大影响.一般认为，过拟合效应所带来的白噪声一般符合白噪声属性[20].广义的自回归条件化异方差(GARCH)模型能够较好地描述过拟合效应中波动量vt的概率分布，如下所示：

(10)

(11)

式中：zt为t时刻符合标准正态分布的数集；ht为t时刻vt的中间变量；E为期望值计算；Ft-1为(t-1)时刻波动量vt-1对应的F检验标准值.

基于条件化的异方差模型，本研究所采用的波动分析模型考虑了不同时刻的行程时间数据所对应的不同条件变量，通过异方差模型模拟波动性变量vt在不同时刻的概率分布.

Bollerslev[27]首次提出可采用广义的自回归条件化异方差模型来模拟噪声分布，该模型适用性较广，但没有考虑原数据的不对称性，而研究路段的行程时间具有明显的潮汐性，因此该方法并不适用.Glosten等[28]在Bollerslev研究的基础上提出了GJR-GARCH模型，通过引入新的二维条件变量，获取股票数据初始预测误差中的不对称特性，并通过正变量和负变量的交替以及不同时段下系数与波动量的交叉修正，缓解了多步预测时误差在传播过程中所产生的振荡，对过拟合所形成的多余噪声进行了平滑修正，从而很大程度上缓解了过拟合效应，表达式如下所示：

(12)

式中：G为常数；l为系数βj对应的波动平滑时段；βj为与j时刻交叉对应的中间变量ht-j的非负平滑系数；Q为系数αk和γk对应的波动平滑时段；αk为与k时刻交叉对应的波动量vt-k的非负平滑系数；γk为与k时刻交叉对应的引入修正变量的波动量vt-k的非负平滑系数；λt-k为(t-k)时刻关于波动量vt-k的二元修正变量.λt-k的表达式如下所示：

(13)

当所有γk均为零时，GJR-GARCH模型转变为标准化的GARCH(l,Q)模型.本研究中将采用该模型对行程时间预测中可能产生的过拟合效应进行缓解.

3 模型结果分析

3.1 计算过程与参数标定

3.1.1改进的小波神经网络模型

基于组合模型WNN-MKC-GJR的架构，对行程时间数据进行组合预测.本研究选用的WNN模型的输入层为所选路段的历史行程时间数据.根据数据筛选，将3月至7月的每周二到四的行程时间数据作为训练组，将8月前12个研究日的数据作为测试组，输出层为第13个研究日，即8月28日的行程时间预测值.将行程时间波动较大的路段D作为目标路段，用以检验波动性分析模块的有效性.以路段D上游的路段A、B、C以及下游的路段E作为关联路段，通过改进的动态小波变换函数对关联路段进行动态权重赋值.五条路段的历史行程时间数据的中值统计情况如图3所示.

图3 五个路段的历史行程时间数据分布

图3中,每个时间点对应的行程时间值为2008年1月—8月中所有对应时间点的行程时间值的平均数.由图3可以看出，各个路段上每天均有3 h左右的波峰时段，即高峰拥堵时段，但在出现的时间上有先后差异.路段A的行程时间在15∶00左右开始增加，16∶30左右达到峰值，并在18∶00左右完成拥堵消散.路段B、C的行程时间同样在15∶00开始呈现上升趋势，17∶30左右达到峰值，并在19∶00左右恢复平峰速度.路段D、E的行程时间在16∶00左右开始上升，较前三个路段晚了1 h，峰值在17∶30左右产生，拥堵结束时间为19∶00左右.五个路段的行程时间在时空分布上具有相似性和传递性，因此相互之间有着较强的相关性.基于此相关性，在小波神经网络中可将其中几个路段作为关联路段，将剩下的路段作为目标路段进行训练，以提高预测精度.路段D上的行程时间波动较大，可用来检验波动分析模块的有效性.因此,以路段D为目标路段，以路段D上游的路段A、B、C以及下游的路段E作为关联路段，通过改进的动态小波变换函数对关联路段进行动态赋权.

3.1.2马尔可夫链模型

在小波神经网络模型得到初步预测值之后，采用马尔可夫链对初步预测值的对应相对误差进行修正，t时刻相对误差Zt3的表达式如下所示：

(14)

式中：Zt1和Zt2分别为t时刻行程时间的实际值和小波神经网络预测值.

根据基于二叉判定图[26]的划分方法对数据链进行状态划分，将初始预测值对应的相对误差集合划分为九个状态(s1,s2,…,s9)，具体对应区间如表1所示.

基于状态划分结果，分别建立小波神经网络测试组在15∶30—19∶30各个时刻的状态分布矩阵.将15∶30的状态分布矩阵作为初始状态矩阵S0，并构建马尔可夫链一步转移概率矩阵P，如下所示：

(15)

表1 马尔可夫链状态划分

基于切普曼-柯尔莫哥洛夫方程，可得到8月28日15∶30—19∶30每隔5 min的时刻点对应的预测相对误差值.

3.1.3GJR-GARCH模型

不同的(l,Q)组合下，GJR-GARCH模型的噪声削减效果不尽相同.Zhang等[20]指出，当l、Q均为1时，GJR-GARCH(1,1)模型相比于其他参数模型能够更好地应对非对称性较强的行程时间数据，并且具有较好的白噪声削减作用，因此研究也采用GJR-GARCH(1,1)模型作为波动性分析模型.参数估计都采用最大似然估计法，并通过Matlab的“garch”工具箱中的多变量GARCH模型实现GJR-GARCH(1,1)模型的波动性分析功能.

3.1.4对照模型

使用三个经典模型作为组合预测模型的对照组，分别是传统小波神经网络模型、BP神经网络模型以及两步自回归(automatic regression 2-step, AR(2))模型.AR(2)模型的计算表达式如下所示：

H(t)=θH(t-1)+(1-θ)H(t-2)+δ(t)

(16)

式中：H(t)为t时刻AR(2)模型的预测值；θ为平滑权重系数；δ(t)为t时刻的随机噪声.

经过对不同θ的检验测试，当平滑权重系数搜索至0.5附近时，模型的预测表现最佳，并且在(0.50-0.01,0.50+0.01)范围内波动时AR(2)的预测精度区别不大，因此以0.5作为AR(2)模型的平滑权重系数.

除以上三个模型，本研究还将基于BP、AR(2)、MKC和GJR-GARCH模型构建另外两个对照组合模型，因此共有五个对照模型.两个对照组合模型分别是BP-MKC-GJR模型和AR(2)-MKC-GJR模型，结构及计算过程与WNN-MKC-GJR模型类似，波动分析模块均采用GJR-GARCH(1,1)模型.

采用平均绝对误差E1、平均绝对百分比误差E2与均方根误差E3评价模型性能，表达式如下所示：

(17)

式中：n为预测时段内时刻点的总个数.

3.2 预测结果分析

所有模型对2008年8月28日路段D行程时间数据的预测如图4、5所示.

图4比较了各模型预测值与真实值的差异，用于观察各模型的预测精度.图5展示了各个时间点不同模型预测值与真实值的相对误差，用于体现各模型在不同时段的预测稳定性.

如图4所示，在非拥堵时段15∶30—16∶45内，各模型曲线趋于平稳且较为接近，说明该时段内各模型都能较好地预测行程时间；在拥堵时段16∶50—18∶50内，WNN-MKC-GJR组合模型所在的曲线最接近真实值曲线，说明该组合预测模型在高峰时段内有较高的预测精度；AR(2)所在的曲线偏离真实值曲线较多，并且当16∶50行程时间出现突变时，AR(2)对于该拐点的预测滞后于其他五个模型，在拐点的预测误差为62 s，说明AR(2)模型在处理波动性较强的数据时有明显局限性；WNN-MKC-GJR组合模型在拐点 16∶50 预测上没有滞后性，在16∶45—16∶50准确预测了行程时间的突变趋势，在突变点的预测值与真实值最为接近，预测误差为18 s.

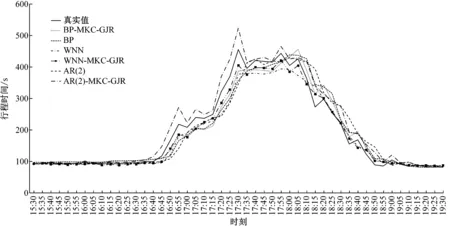
图4 行程时间预测结果

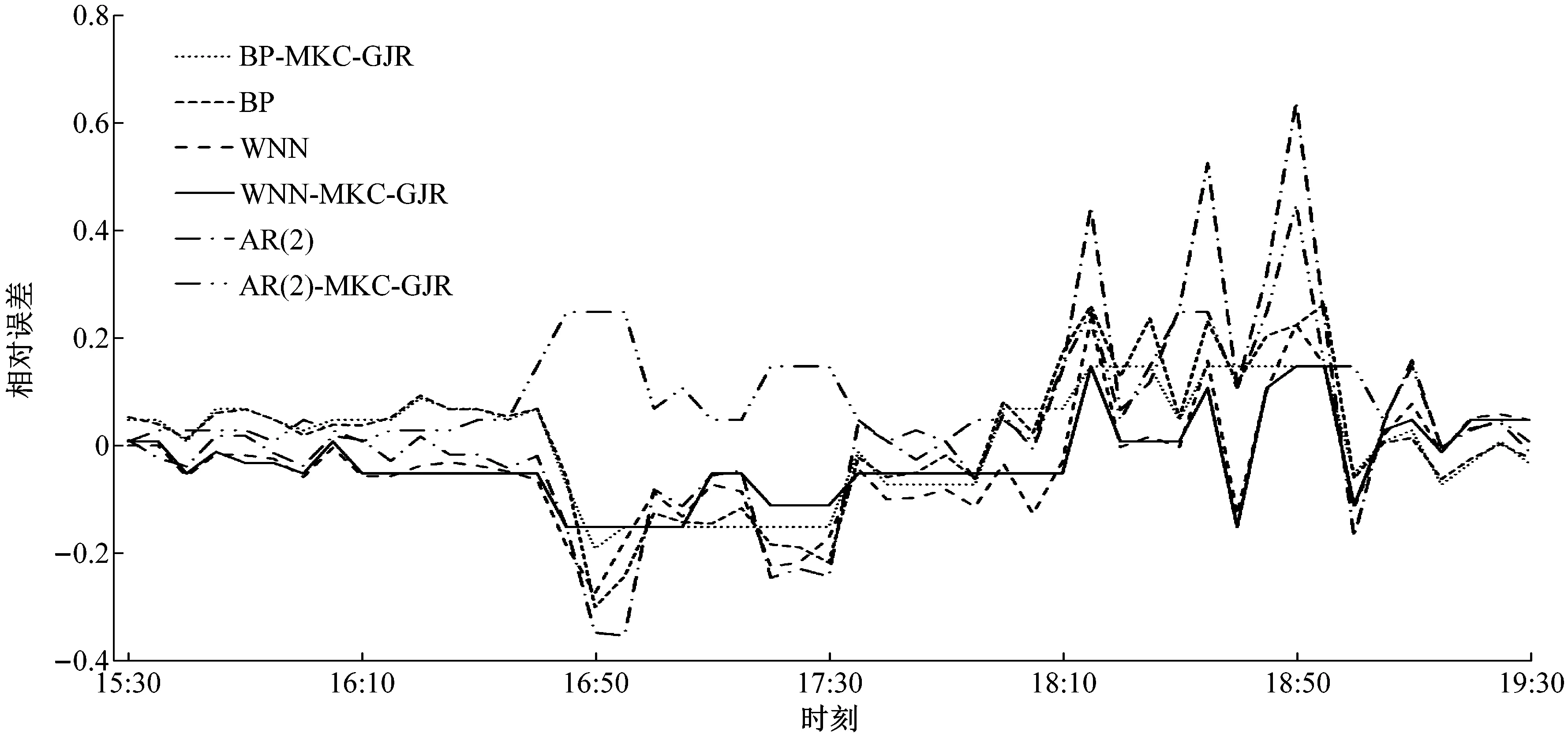
图5 预测的相对误差

如图5所示，非拥堵时段内各模型预测值对应的相对误差波动较小，说明各模型在该时段都有着较好的预测稳定性；在行程时间发生突变的时间点 16∶50，各预测模型相对误差曲线都出现了不同程度的振荡，其中WNN-MKC-GJR组合模型的振荡幅度最小，相对误差为-15%，并且该值在拥堵时段内一直保持相对较低的水平，曲线保持平稳，相对误差极值为26%，说明该组合模型在高峰时段内有着较好的预测稳定性；AR(2)模型在拥堵时段内的相对误差较于其他五个模型偏高，说明该模型的预测稳定性较低.

图4、5表明：在增加马尔可夫链二次修正模块和GJR-GARCH模型的波动性分析模块后，模型的预测精度和预测稳定性较之对应的单个模型都会有不同程度的提升.通过三个指标进一步反映各个模型在不同时段(行程时间突变点前后)内的预测能力，如表2所示.从表2可得出以下结论：

(1) 从整个晚高峰时段来看，WNN-MKC-GJR模型在三个指标下的表现都要好于其他五个模型.在行程时间突变发生之前，基于线性预测的AR(2)模型表现最优，原因在于当行程时间波动较小时，基于线性迭代的预测方法能更好地接近真实值；在行程时间发生突变之后，WNN-MKC-GJR模型明显优于其他模型，说明所提出的组合模型在拥堵时段内有着更好的预测精度.

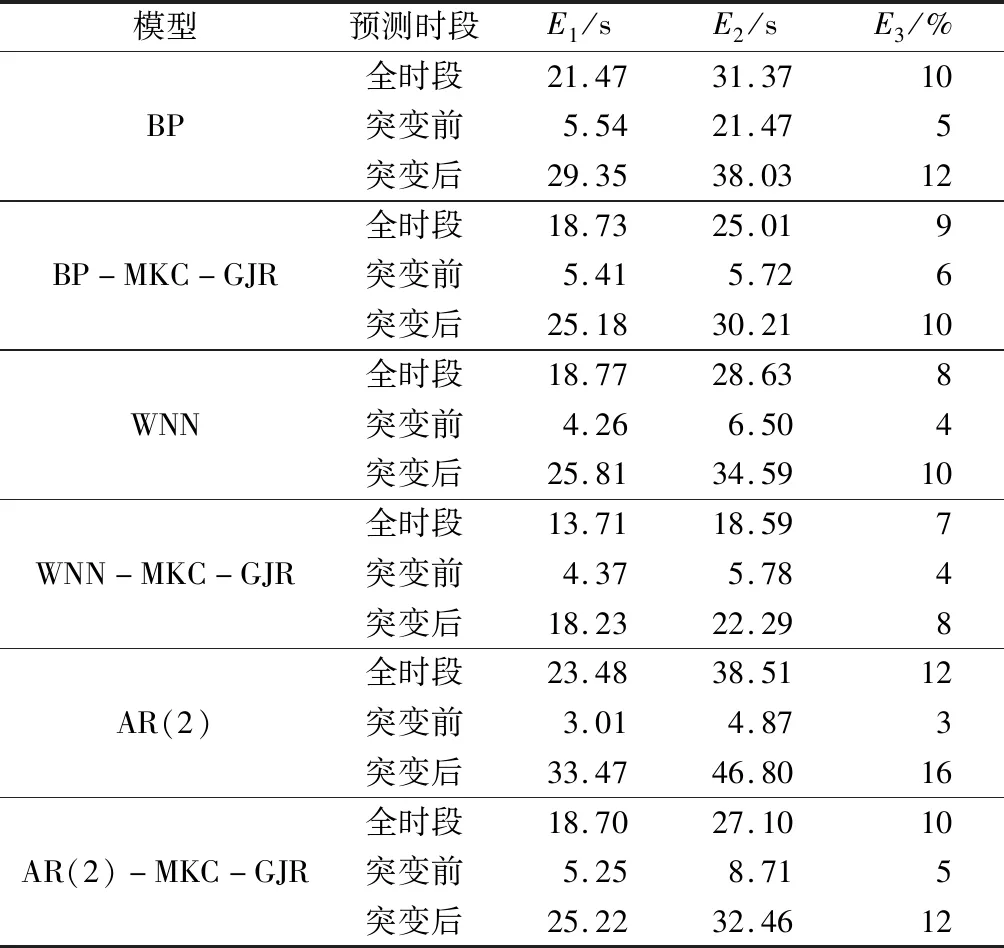
表2 预测性能指标比较

(2) 行程时间突变点之前，在增加MKC-GJR模块之后，WNN、BP和AR(2)模型在三个指标上并未全部提升；在行程时间发生突变之后，MKC-GJR模块对于WNN、BP和AR(2)模型的预测精度均有不同程度的提升，说明马尔可夫链与GJR-GARCH模型的组合可以提升单一模型在拥堵时段内的预测精度.

(3)E3值方面，单个模型在加入MKC-GJR模块成为组合模型之后，某些预测性能上可能会超过原本比自己高级的单一模型，如BP-MKC-GJR在特定时段(全时段和突变后)内三个指标均优于WNN，同时AR(2)-MKC-GJR在任何时段三个指标均优于BP.在实际运营管理中考虑计算时间的约束时，这一个特征也可以为预测模型的选择带来更多的灵活性.

4 结论

(1) 在充分考虑实际运行过程中行程时间周期性、潮汐性、高峰时段不稳定性后，基于周期性预测、残量修正和波动性分析三个部分构建了新的组合架构，采用改进后的小波神经网络、马尔可夫链和GJR-GARCH模型构建了WNN-MKC-GJR组合预测模型.基于相对误差状态构建的马尔可夫链成分使得组合模型无需对复杂的交通状态进行量化判别，因此具有较强的可移植性.

(2) 加入相对误差修正以及过拟合噪声修正这两个模块之后，WNN-MKC-GJR组合预测模型具有更高的预测精度和更强的预测稳定性，这一表现在高峰时段内尤为明显，预测精度和稳定性要明显优于其他五个对照模型.在平峰时段内，线性的AR(2)模型具有较好的预测精度，这表明在平峰时段内采取平稳的时间序列模型会取得更好的预测效果.

(3) 在行程时间发生突变的时刻，WNN-MKC-GJR组合预测模型可以及时捕捉突变的“拐点”，而其他五种模型都有不同程度的预测滞后.在实际城市交通管控策略的实施过程中，若能准确感知行程时间突变(即大规模拥堵可能形成)时刻，则可以提前采取相关的主动管控措施，缓解拥挤的扩散速度，为高速公路交通流运行管理的决策提供依据.

本研究所涉及的路段上交通事件发生数量不多，因此需要在日后的研究中进一步检验组合模型处理交通事件数据的预测能力.