基于滤波算法的分布式云储能系统弹性稳定控制

(1. 常州轻工职业技术学院, 江苏 常州 213164；2. 哈尔滨工业大学 空间控制与惯性技术研究中心,哈尔滨 150000)

0 引言

伴随工业4.0时代的到来，兼并信息网络化与资源整体化的能源电力行业技术也孕育而生，与之匹配的通讯技术和控制策略也不断进步，能源互联网的发展将引领未来电力系统发展的新方向，智能微电网云储能系统的出现为能源互联网提供了一种行之有效的解决方案[1]。智能微电网云储能系统按电源侧安装的位置不同可以分为分布式与集中式两种，与集中式储能不同，分布式储能通常将用户电源安装在用户侧或者微电网中[2]。我国目前即将迎来经济高速稳定发展的历史时期，分布式云储能系统将更加适合未来人们的需求[3]。

目前，基于微电网的运行和控制方面是国内对于分布式储能系统的研究热点[4-7]，与此同时，有关电动汽车供电系统[8]和可再生能源互联网[9]的研究也取得了一些进展。分散控制策略[10-12]和集中控制策略[13-15]是目前两种典型的分布式储能运行决策方法。其中，文献[10]开始考虑多个基本储能单元之间的协调工作关系，通过相邻单元彼此之间的迭代协调达到整个系统的最优控制策略，为分布式云储能系统理论的建立提供可能。接下来，一种多代理合作控制策略在文献[11]中被提出，用以平衡直流微电网中基本分布式储能单元之间的瞬时功率。文献[12]针对低压配智能微电网中存在的电压跃升和跌落问题研究了分布式储能局部控制与单独控制的方法，使得该类系统可以工作在高光伏渗透率的环境中。文献[13-14]分别利用分布式储能规划运行最优解和联合运行优化的方法对控制系统外部参数进行设置。在经济价值方面，文献[15]给出智能微电网分布式电池储能系统在单位电价基础下的套利问题，将权衡经济价值和电池使用寿命问题综合考虑，最终得到基于最优控制理论的套利策略。

本文从分布式云储能系统中一个基本单元的数学建模出发，为寻求该类系统在充放电之间电压电流稳定工作时的平衡点，将采用分段仿射静态输出反馈控制方法实现系统镇定，进而建立该类云储能系统在充放电之间的安全机制。在此基础上，应用分段仿射系统鲁棒H∞控制方法给出分布式云储能系统稳定的充分必要条件。本文所考虑智能微电网分布式云储能系统模型如图1所示。

图1 智能微电网分布式云储能系统模型

1 数学建模

本文所考虑智能微电网分布式云储能系统中的基本储能单元充放电过程模型如下图2所示，当基本单元中能量在J0位置时，该系统在此时充放电达到平衡，此时电压、电流变化率趋近于零，充电、放电电量差值变化在此刻也趋近于零。控制目的在于稳定围绕能量平衡点J0处波动的工作状态，在反复波动的充放电过程中，使得充放电电压、充放电电流以及充放电电量差值变化作为系统状态的闭环系统渐近稳定。

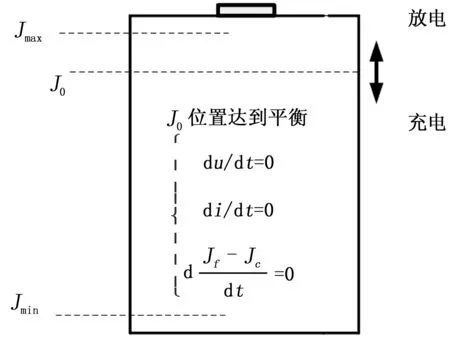
图2 基本储能单元模型

图2中其他各物理量的定义如表1所示。

表1 各物理量的具体含义

其中，我们取Uf为系统的输入变量，并采用一个可控阀门对输入变量进行调节，基本单元放电Uc电压通常取为一个常数。Ic和If代表平衡点处储能单元充放电时流经电网的电流，Jmax和Jmin用来表示整个过程中基本储能单元能量的最大值和最小值。

基本储能单元模型作为分段仿射系统理论最典型的应用，即在广义矩阵E=I情况下描述的一般形式的控制系统。在本文中，解决此类分段仿射控制系统具体问题的途径是通过寻求系统各变量之间的关系式，采用变量替换的方法构造形式上的广义系统，最后应用本文主要结果对所提广义分段仿射系统控制问题进行分析处理。

在采样时刻T的作用下，我们可以将如图1所示云储能基本单元系统按照平衡点J0进行分类，具体表示为如下两个子系统(J>J0对应Χ1，J≤J0对应Χ2)的PWA模型：

(1)

针对如图1所示的基本储能单元模型，考虑控制系统存在随机扰动的情况，且扰动w(k)的形式为随时间不断衰减的噪声信号。另一方面，考虑系统存在范数有界形式的不确定性，则此类储能单元模型可以归纳为如下一类具有范数有界参数不确定性的离散时间广义分段仿射系统：

(2)

其中：x(k)∈Rnx为系统状态变量；u(k)∈Rnu为控制输入向量；y(k)∈Rny为系统输出向量；z(k)∈Rnz为可控输出向量；w(k)∈Rnw且w(k)∈l2[0, ∞)为扰动输入；Ai,Bi,Ci,Di1,Gi,Di2,bi,E为第i个子系统的已知定常系数矩阵；Ebi是偏置项；索引集合是I={1,2,…,N}；E∈Rnx×nx是广义矩阵，且rank(E)=r≤nx；ΔAi和Δbi代表系统的不确定项，且满足如下形式：

[ΔAiEΔbi]=Wi1Δi(t)[Ei1Ei2],i∈I

(3)

其中：Wi1,Ei1和Ei2是具有适当维数的已知实定常矩阵，Δi(t):Z+→Rs1×s2是一个包含Lebesgue可测量元素的未知实值时变矩阵函数，具有如下形式；

(4)

如果式(2)和式(3)成立，则称系统的参数不确定性是容许的。

令Ω代表子系统从多面体区域Ri过渡到Rj的集合，可以描述为：

Ω={(i,j)|y(k)∈Ri,y(k+1)∈Rj,i,j∈I}

(5)

本文假设多面体区域Ri,i∈I具有形式：

Ri={y|αi≤y≤βi,y=Cix},i∈I

(6)

εi={x|‖Fix+fi‖≤1},i∈I

(7)

对于每个椭圆区域，可以得到；

本文针对给定的常数γ>0，取z(k)为待估计信号向量，设计一个渐近稳定的弹性H∞滤波器：

(8)

其中Af,Bf,Cf,Df为弹性滤波器的待定系数矩阵.渐近稳定弹性H∞滤波器反馈环节不确定性BiΔKi=Wi1Δi(t)Ei3,i∈I。

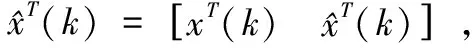
(9)

2 预备知识

本文假设系统(1)的输入矩阵Bi,i∈I是列满秩的，在此假设条件下，则存在一组转换矩阵TBi∈Rnx×nx,i∈I，满足：

(10)

其中：TBi∈Rnx×nx非奇异，以下弹性H∞滤波器就是基于该假设进行设计的。

定理1:考虑参数不确定离散广义分段仿射系统(1)，若存在对称矩阵H1,H3∈Rnx×nx,标量{λij<0，i∈I1，(i,j)∈Ω}，实数γ∈R, {εij,i∈I, (i,j)∈Ω}，以及滤波器待定参数矩阵：Af∈Rnx×nx,Bf∈Rnx×nx,Cf∈Rnx×nx,Df∈Rnx×nx，H2∈Rnx×nx,Ki∈Rnu×nx，使得：

(11)

<0,i∈I1,(i,j)∈Ω

(12)

成立，则存在H∞渐近稳定弹性滤波器(8)，使得滤波误差动态系统(9)是容许的，且扰动w到估计误差传递函数的H∞范数小于给定的常数γ。

证明：

首先，通过滤波误差动态系统(9)的系统描述寻求适当的Lyapunov函数.选取广义分段仿射Lyapunov函数：

(13)

进一步构造ΔV(k)：

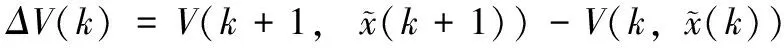
(14)

基于Lyapunov函数的定义，为使滤波误差动态系统(9)具有鲁棒H∞性能指标γ，则我们只需保证以下不等式成立：

(15)

(16)

考虑滤波误差动态系统(9)，对于任意非零w(k)∈l2[0, ∞)，(15)可进一步等价于：

(17)

用矩阵形式将式(17)改写，可进一步得到：

(18)

从式(18)，我们可以得到：

(19)

即：

(20)

(21)

(22)

考虑区域信息，即将式(7)带入式(18)并应用引理3，其中λij<0,i∈I1, (i,j)∈Ω，得到:

< 0,(i,j)∈Ω

(23)

对(23)式中各个矩阵进行合并，并先后应用2次Schur补引理，从式(23)可以得到:

< 0,(i,j)∈Ω

(24)

另一方面，由于本文所考虑的广义分段仿射系统具有参数不确定性，为消除不确定性给求解过程带来的影响，将(24)式中的不确定性ΔAi和EΔbi分离出来，下面可以将(24)式改写为：

(25)

进一步得到：

< 0,(i,j)∈Ω

(26)

(27)

定理得证。

3 数值仿真

为了验证本文所提基于观测器H∞控制器设计方法的实用性，下面考虑一个实际物理映射，并将通过对其滤波器增益以及反馈控制增益的求取证明定理1的有效性。最后。通过两种供电模式能耗比例的对比证实本文所提方法的卓越性。

考虑由两个基本储能单元构成的分布式云储能系统，令x1(k)代表放电电压变化率，x2(k)代表充电电流变化率，x3(k)代表放电电流变化率。将扰动输入取为随时间延续不断衰减的白噪声信号：w(k)=e-5k，则离散化得到系统模型：

其中：取系统状态初始值为x(0)=(2.5,1,-1),其他参数取值如下：

E12=0.03，E22=0.04，

椭圆体系数矩阵通过公示可计算得到：

其中：α1=3,β1=10,α2=4,β2=9。

应用定理1得到一组使闭环系统(9)容许基于滤波器的H∞控制器反馈增益矩阵：

H∞干扰抑制度γ=6.5896。

图3为根据定理1得到的由基于滤波器H∞控制器所构成闭环系统(9)的状态响应曲线：

图3 根据定理1得到的系统状态响应曲线

图3所示仿真结果表明：定理1方法可以保证分布式云储能系统在充放电平衡点处可以安全稳定的工作，且整个系统在渐近稳定的过程中扰动w到估计误差传递函数的H∞范数小于给定的常数γ。

接下来，我们将比较两个独立储能单元在各自独立工作和联合工作两种模式中各自的优缺点，能量来源以及充放电过程能量走向如图4所示。

图4 分布式云储能系统能量循环模式

实验中我们采用容量为200wh/kg的钴酸锂电池独立供电，且智能微电网分布式云储能系统由两个用户组成。我们假设两个用户在同样条件下获得的风能发电与太阳能发电电量相同，用户1日用电量较大(约20kw/h)，用户2日用电量较小(约5kw/h)，我们在连续24小时范围内，将测得两个用户在充放电过程中能量供应和损耗绘制成图表，如图5所示。

图5 独立供电模式中能耗比例

通过测量，在两个基本储能单元独立供电的情况下，用户1能量总消耗量在20.5 kW/h，其中常规电力系统供电约14.76 kW/h，风能和太阳能供电占约5.74 kW/h；用户2能量总消耗量在5.2 kW/h，其中常规电力系统供电约3.12 kW/h，风能和太阳能供电占约2.08 kW/h。由于两个用户风能和太阳能采集条件的一致性，两种能量用户1消耗的总数要大于用户2，通过最终两个用户的能耗比例也可以表明：在采样24小时过后，用户1由于用电量较大的原因，在附能提供一样的前提下，多消耗了12%的常规电能，造成一定程度上传统能量的损耗，而用户2没有消耗的多余附能又没有能够及时使用，造成能源利用率的降低。进一步，采用本文提出分布式云储能方式协调两个用户的总体用电量，重复上述相同实验。

图6 分布式云储能供电模式中能耗比例

图6表明：在两个用户总能耗25.7 kW/h不变的情况下，最终测得常规电力系统供电约16.448 kW/h，占比总能量供应的64%，节约1.43 kW/h。最终结果表明：采用分布式云储能方式协调两个用户的总体用电量是行之有效的，并且充分利用了可再生资源，节约传统电力系统供电资源，有效的缓解传统电力系统负载压力，有利于环境保护。

4 结论

本文针对目前智能微电网分布式云储能系统运行架设成本较高且难寻行之有效整体控制规律的问题，将一种体现为具有范数有界时变参数不确定性的分段式储能系统引入基于滤波器的H∞控制器设计方法。基于广义分段仿射Lyapunov函数，投影定理以及几个基本引理，设计了使参数不确定离散时间广义分段仿射系统容许的基于滤波器的H∞控制器，保证了由此构成的闭环系统具有一定的鲁棒性能。算法以LMIs约束的形式给出了基于滤波器H∞控制器存在的充分条件，并且不包含对系统矩阵的分解，减低了算法的保守性，最后数值仿真给出了基于滤波器的H∞控制器的最优解，同时获得了控制器输出反馈增益和滤波器矩阵，并使得闭环系统保守性有所下降。仿真证明了设计方法的有效性。

与此同时，通过对两种供电模式能耗比例的对比结果证明本文所提方法的有效性和卓越性，通过两种供电模式耗能比例的的分析，证实智能微电网分布式云储能供电模式可以合理有效的利用和平衡各类资源，达到间歇性可再生资源利用的最大化。