均匀温度下多跨半刚接整体桥受力性能
许 震, 罗小烨, 陈宝春, 黄福云
(1. 福州大学土木工程学院, 福建 福州 350108; 2. 盐城工学院土木工程学院, 江苏 盐城 224051)
0 引言
无伸缩缝桥梁是指两引板(搭板)末端范围内上部结构为连续结构、 无伸缩装置的桥梁, 简称无缝桥[1]. 它主要有整体桥、 半整体桥和延伸桥面板桥等三种. 与有缝桥相比, 无缝桥行车舒适, 车辆冲击小, 养护费用省, 结构耐久性好[2-5]. 可用于新建桥梁中, 而且在既有桥梁改造中也发挥着重要的作用[6-7].
对于多跨空心板简支梁桥, 可采用无缝化技术将其改造为无缝桥[8]. 其中, 整体桥的使用性、 整体性、 耐久性和抗灾能力最优, 是无缝化改造中优先选择的桥型[9-10]. 然而, 我国的实际应用中多改造为延伸桥面板桥[11-12]. 将其改造为整体桥的, 目前仅见一例, 且尚未开展深入的研究[13]. 同时, 该桥在整体化改造中, 桥台、 桥墩处均采用了半刚性连接, 构思新颖, 与全刚接整体桥受力有相当的不同[14-16], 对其受力性能开展深入的研究, 有助于今后的推广应用. 本文应用ABAQUS有限元软件, 建立整体桥精细有限元模型, 重点分析连接形式与节点构造参数对结构受力性能的影响, 为今后类似桥梁整体化改造设计提供参考.
1 工程背景
某桥建于20世纪90年代, 共3跨, 为16 m钢筋混凝土简支空心板, 钢筋混凝土柱式桥墩连接灌注桩基础, 埋置式桩柱桥台, 同样采用灌注桩基础. 经多年运营, 空心板出现较多病害, 上部结构技术状况评分仅30.8分, 定为五类桥, 决定进行改造. 由于下部结构状况较好, 予以利用, 仅对上部空心板梁进行更换, 并改造为半刚性节点整体式无缝桥, 改造的详细方案见文献[13]介绍, 改造前、 后的桥梁总体布置见图1. 该桥改造后开放交通3年多来, 桥面平整光滑, 无裂缝出现, 桥况良好.

图1 桥梁总体布置(单位: mm)Fig.1 Elevation of the bridge(unit: mm)
2 精细有限元模型
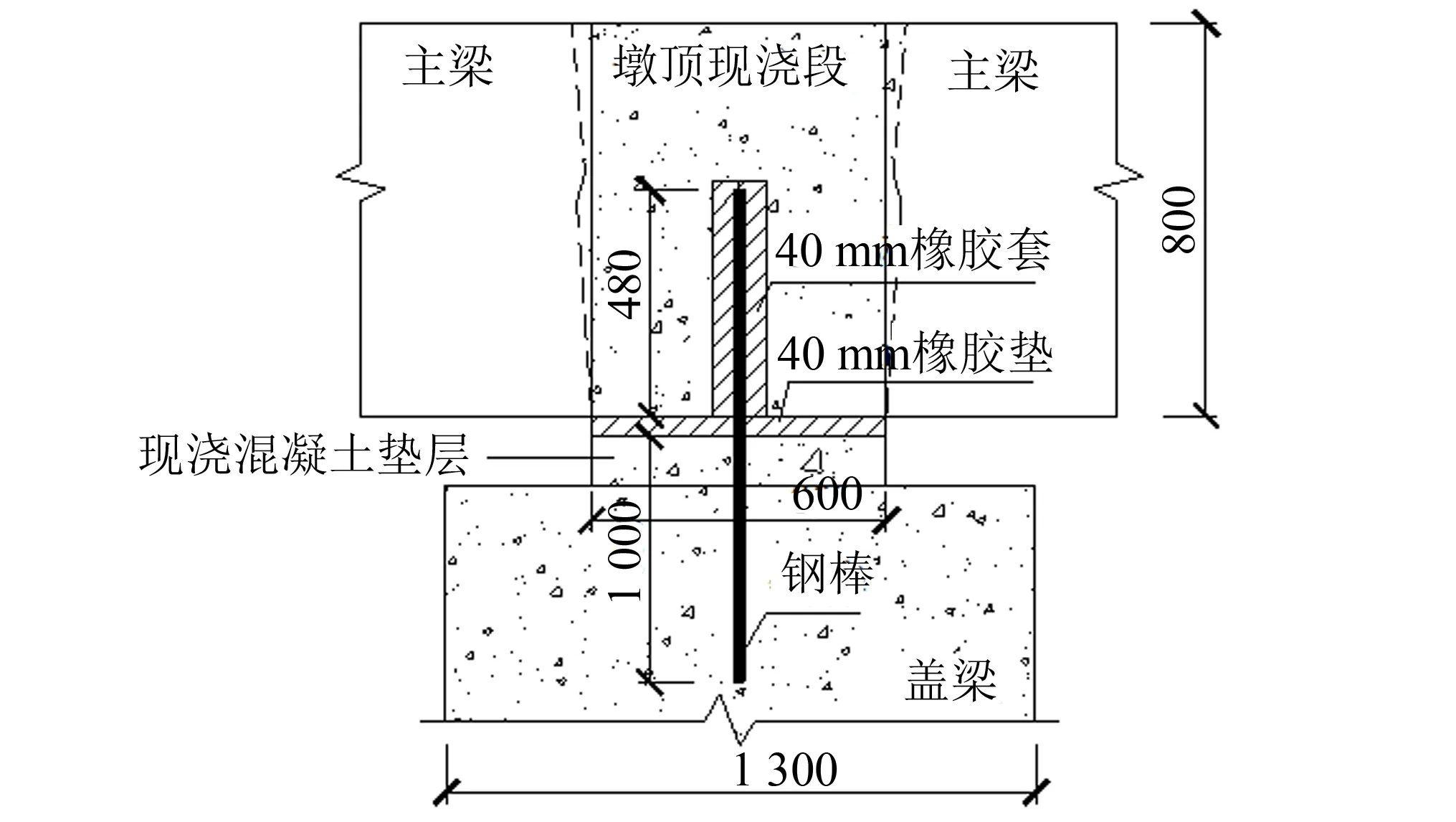
图2 桥墩半刚性节点(单位: mm)Fig.2 Semi-rigid joint on pier(unit: mm)
2.1 节点有限元验证
桥墩处半刚性节点细节尺寸如图2所示, 其中, 钢棒(直径D=32 mm)横桥向间隔400 mm设置一根, 桥台处的钢棒构造与之相似. 为分析半刚性节点对桥梁结构受力影响, 对原桥半刚性节点进行足尺模型试验, 图3为试验模型及测点位置. 利用ABAQUS[17]对该节点进行有限元模拟, 材性参数见表1. 橡胶材料采用Mooney-Rivlin本构模型[18](其中参数C10=0.47,C01=0.12,D1=0).
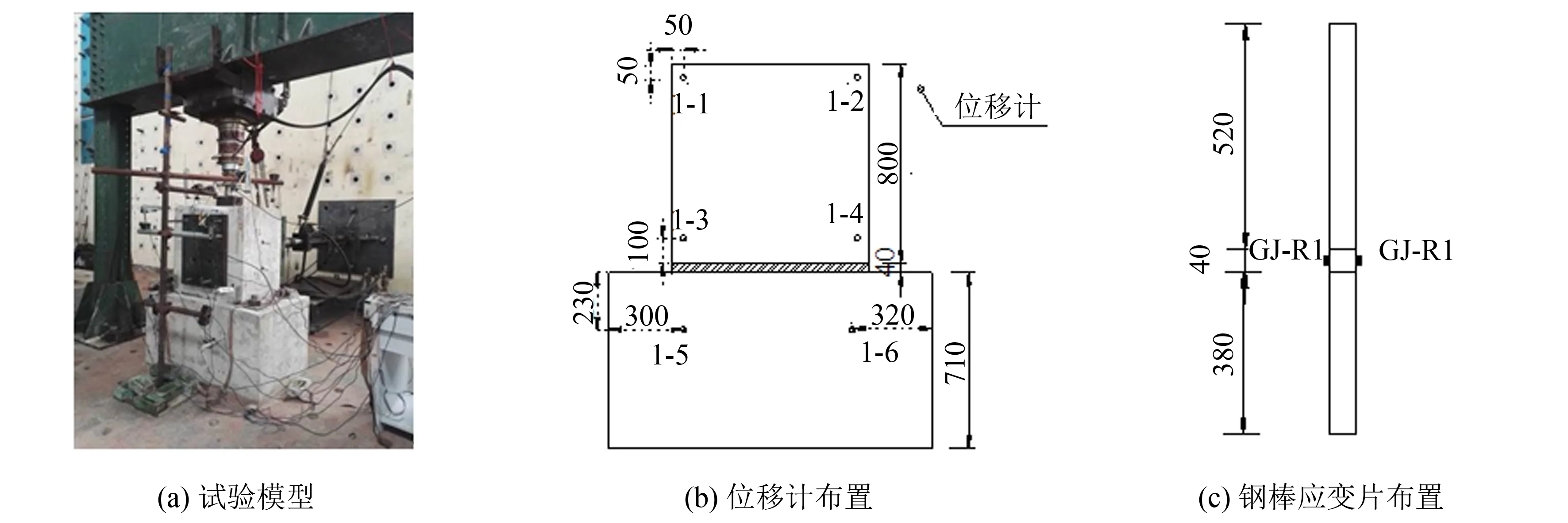
图3 试验模型及测点位置(单位: mm)Fig.3 Test model and measuring point location(unit: mm)
图4(a)为节点上1-1测点实测值与有限元值对比, 由图4(a)可知, 实测值与有限元值曲线基本保持一致, 最大值相差约为3.9%. 图4(b)为MTS加载位移和对应力与有限元的加载位移和对应力的比较, 从图4(b)可知, 在相同加载位移下, MTS加载力与有限元加载力两者之间最大相差约为4.7%, 曲线基本保持一致. 图4(c)为钢棒的实测应变值与有限元钢棒应变值对比, 在开始加载时, 钢棒应变为弹性, 加载至6 mm后, 应变基本保持不变, 此时, 钢棒进入塑性, 实测值与有限元值最大相差约为7.4%.
由图4实测值与有限元值对比表明, 该节点相应的参数能够用于后面的实桥有限元模拟.

图4 实测值与有限元值Fig.4 Measured value and finite element value
2.2 实桥有限元

图5 实桥有限元模型Fig.5 Finite element model
为了利用2.1节的节点参数, 为此, 全桥应用ABAQUS建立有限元实体模型, 采用C3D8R单元, 由于对称性, 仅建立了一半长度, 共有137 029个单元.
建模时, 桥墩和桥台的盖梁与钢棒连接处单元局部细化. 墩柱与桩及桥台与桩长为20 500 mm(大于等代桩长[16]), 台、 桩周围土弹簧刚度按文献[19]中“m”法确定, 本文m值取为15 MN·m-3. 有限元模型如图5所示.
实桥的接触、 约束类型见表2. 边界条件为桩底固结, 上部结构第二跨跨中对称约束. 根据桥台与桥墩处采用刚接与半刚接, 该桥可以有如下四种连接方式.
A组: a-1, 上部结构与桥台半刚性连接, 与桥墩半刚性连接(实桥, 半刚接整体桥); a-2, 上部结构与桥台半刚性连接, 与桥墩刚性连接(半刚接刚构整体桥).

表2 接触及约束类型
B组: b-1, 上部结构与桥台刚性连接, 与桥墩刚性连接(全刚接整体桥); b-2, 上部结构与桥台刚性连接, 与桥墩半刚性连接(刚接半刚构整体桥).
其他三种连接形式的桥梁结构建模与实桥相似. 结构建模完全相同, 上、 下部结构采用半刚性节点连接的, 其节点及约束类型与原桥建模方式相同, 刚接的则采用绑定(Tie)约束.
3 均匀温度变化作用下的受力性能
整体桥由于纵桥向取消了伸缩装置, 均匀温度变化产生的附加力是其受力的主要特征, 以温升25 ℃对四种连接方式进行计算对比. 由于对称性, 降温效果与升温结果相反, 受篇幅限制这里不再列出.
3.1主梁轴向力
均匀升温25 ℃时, 四类连接的主梁所受的轴力大小分别为79.7 、 77.6、 212.8和218.1 kN. 由此可知, 桥台处的连接方式对受力的影响较大. 刚接时(B组)附加轴力较大, 其中, b-2连接的轴力最大值为218.1 kN; 半刚接时(A组)较小, 其中, a-1连接的轴力最大值为79.7 kN. 前者为后者的2.74倍. 显然, 桥台处采用半刚接(A组)对此项受力有利.
3.2 主梁弯矩
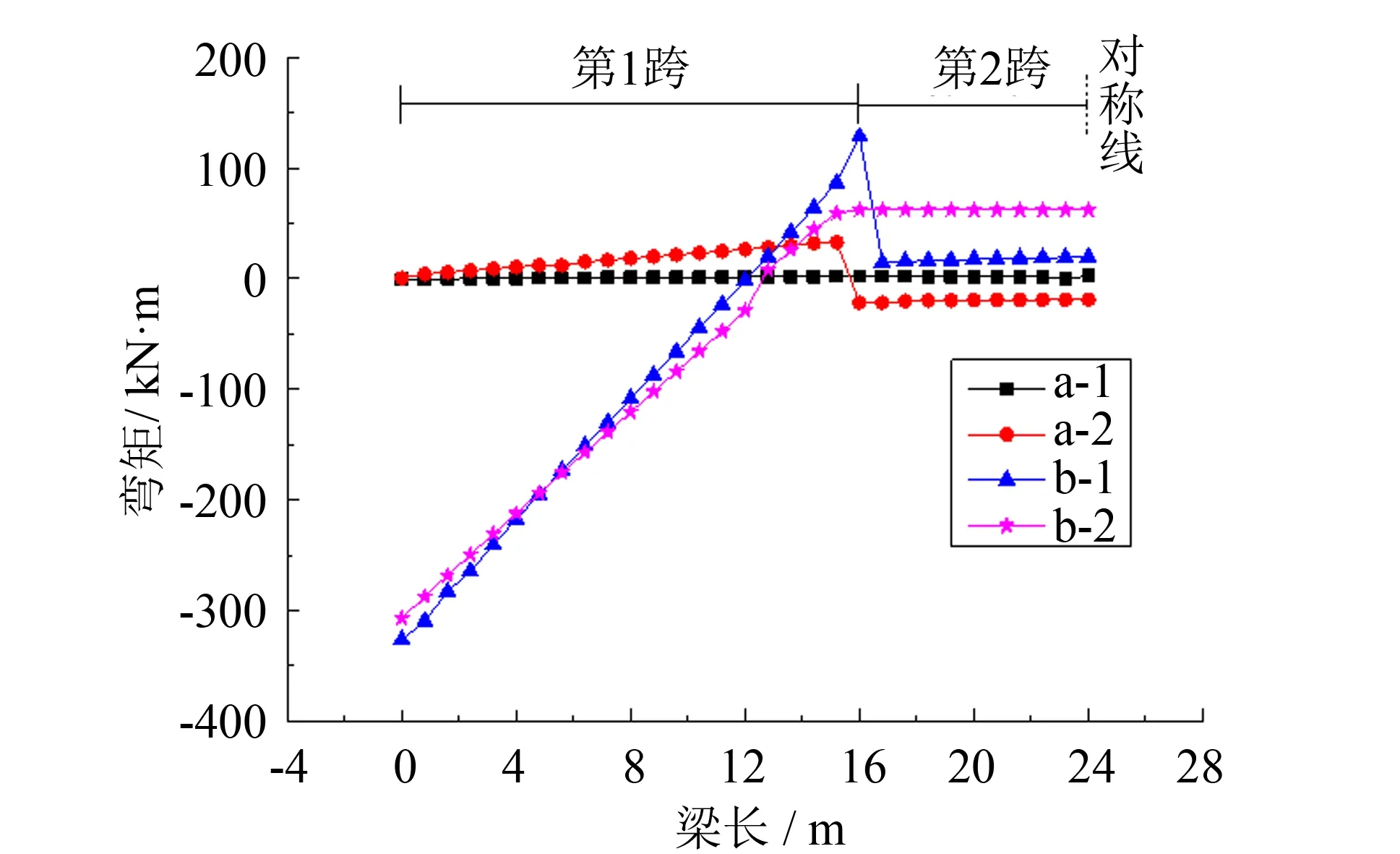
图6 主梁弯矩 Fig.6 Bending moment of main beam
图6为均匀升温25 ℃时的主梁弯矩值. 由图6可知, a-1连接的第1跨和第2跨主梁弯矩几乎为零, 因为主梁的边界约束全部为半刚接形式, 该连接形式对主梁的约束较小. a-2连接的次之, 但由于a-2在桥墩处刚接, 桥墩对主梁约束, 从而桥墩处主梁出现弯矩, 其最大值为32.9 kN. 影响最大的是B组的主梁, 其中b-1连接形式主梁受温度影响最大, 在桥台处梁端弯矩值为326.4 kN·m, 桥墩处主梁弯矩值为128.4 kN·m.
然而, 升温时, B组主梁, 边跨中产生的是负弯矩, 可抵消部分在恒载作用下产生的正弯矩, 对受力有利. 而在降温时, 会加大边跨的正弯矩. 因此, 总体来说, 对于主梁弯矩, a-1连接的受力有利.
3.3 主梁及盖梁位移

表3 主梁、 盖梁最大位移
表3为主梁、 盖梁最大位移值, 从表3中可看出, 四类连接的各种位移, 也可以分为A、 B二组. 两组的主梁端部位移相差不大.
桥墩盖梁位移a-2连接大于a-1连接, 相差约为4.5%, 桥墩盖梁处位移b-2连接小于b-1连接. 桥台盖梁位移, A组约为B组的一半, 这是因为A组的主梁与桥台为半刚性连接, 包裹于钢棒的橡胶套吸收了部分变形所致.
3.4 柱-桩基弯矩与变形
图7~8为均匀升温下, 桥台和桥墩柱-桩基弯矩与变形分布图.

图7 柱-桩基弯矩Fig.7 Bending moment of column-pile foundation
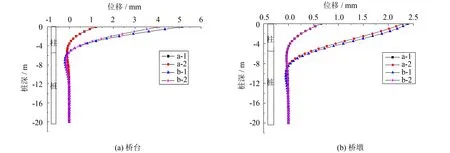
图8 整体温度下柱-桩基位移Fig.8 Displacement of column-pile foundation
在图7(a)和图8(a)中, 四条曲线可以分为A、 B两组, A组弯矩和变形值小于B组. b-1连接产生最大弯矩和变形, 最大弯矩为-415.0 kN·m, 出现在距桩顶-3.0 m处; 最大变形出现在桩顶处, 其值为5.1 mm. 由图7(b)和图8(b)可看出, 桥墩的柱-桩中, 弯矩值与变形从小到大排列分别为: b-2, a-1, a-2, b-1. 最大弯矩与变形均出现在b-1桩的桩顶0.5 m处, 前者为184.2 kN·m, 后者为2.3 mm.
4 半刚性节点参数对受力性能影响分析
由上节分析可知, 实桥的连接方式, 有利于结构受力. 本节以采用该连接方式的实桥为对象, 分析半刚性节点的参数对结构受力的影响. 半刚性节点的参数主要有钢棒直径、 橡胶套壁厚和橡胶垫厚度等.
4.1 钢棒直径
图9(a)为钢棒直径D变化时, 梁端、 第一跨跨中和内支座(桥墩)处主梁弯矩变化值. 由图9(a)可知, 钢棒直径对主梁弯矩影响很小. 一方面, 较厚的橡胶套削弱了钢棒直径变化的影响, 另一方面, 钢棒抗弯刚度与主梁或下部结构抗弯刚度比值较小.
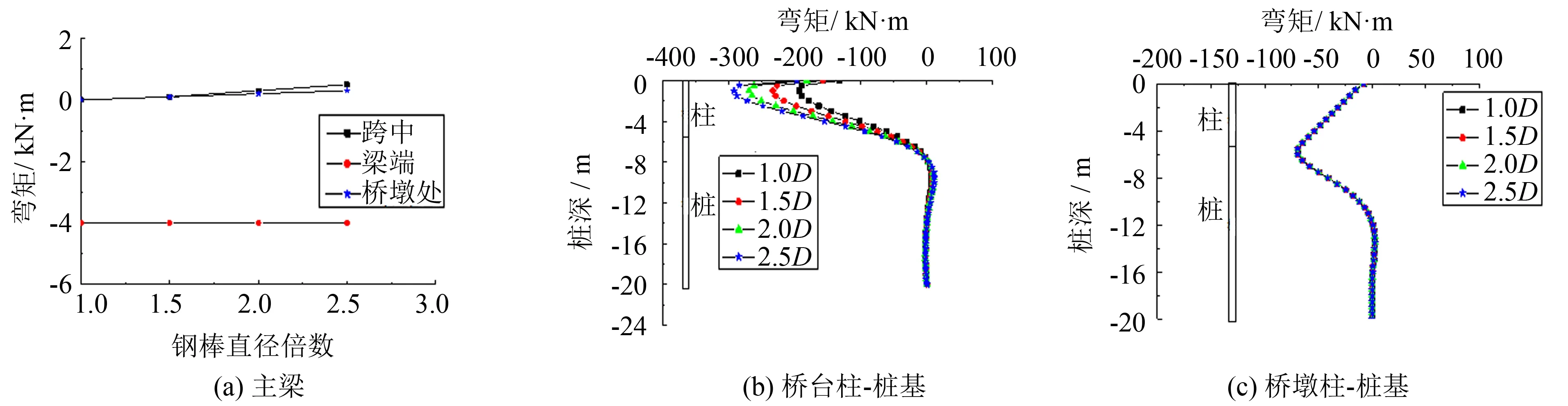
图9 弯矩与钢棒直径的关系Fig.9 Relationship between bending moment and steel bar diameter
图9(b)为钢棒直径增大时, 桥台处下部结构弯矩值相应增大, 最大值出现在柱顶下约1.0 m处, 这是由于橡胶套的存在, 上部结构的部分水平位移通过钢棒传递到下部结构, 在台后土的约束下引起弯矩的变化; 图9(c)为钢棒直径增大时, 桥墩处下部结构弯矩几乎不变, 最大弯矩发生在柱桩连接处, 最大值约为69.3 kN·m.
4.2 橡胶套壁厚
以橡胶套壁厚(T)为参数, 计算得到的梁端、 第一跨跨中和内支座(桥墩)处主梁弯矩见图10(a). 橡胶套厚度为零(无橡胶套)时, 主梁端部负弯矩在三者中最大, 达82.9 kN·m; 随橡胶套壁厚的增加, 梁端、 跨中及墩定处主梁弯矩增量明显减小. 当橡胶套厚度达到40 mm时, 能基本满足变形的需要, 半刚性连接退化为滑动支座, 主梁在纵桥向几乎可以自由伸缩, 在结构中没有弯矩产生.
图10(b)为橡胶套壁厚减小时, 桥台处下部结构的弯矩值增加, 其最大值出现在柱顶下约1.0 m处, 这是由于橡胶套壁厚的减小, 上部结构的位移传递给下部结构的位移增大, 引起下部结构的弯矩随橡胶套壁厚的减小而增加. 图10(c)为橡胶套壁厚改变时, 桥墩处下部结构的弯矩值几乎不变, 最大弯矩发生在柱-桩连接处, 最大值约为72.1 kN·m.
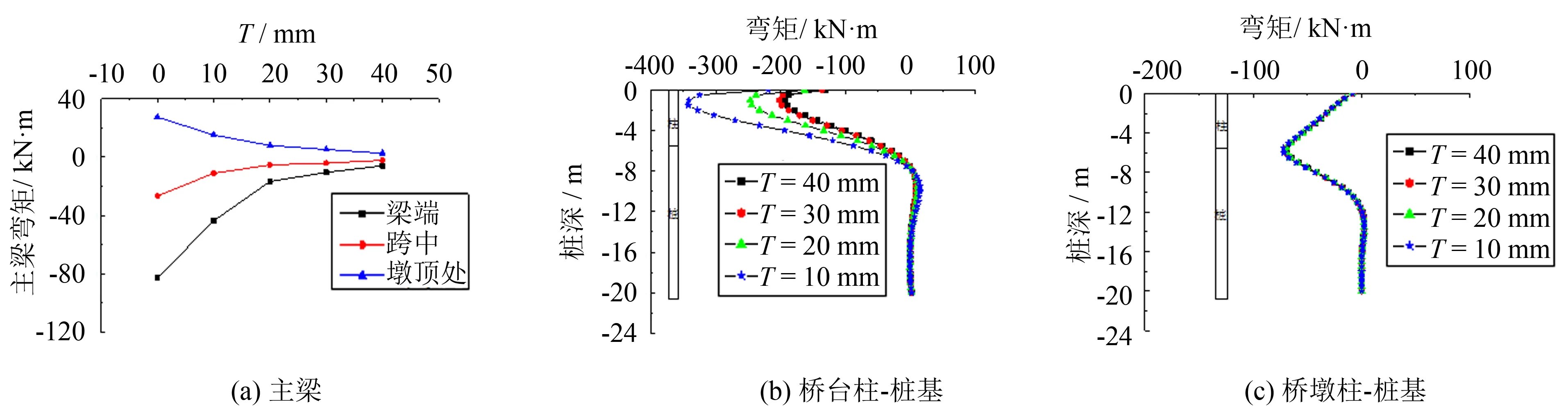
图10 弯矩与橡胶套壁厚的关系Fig.10 Relationship between bending moment and rubber sleeve thickness
4.3 橡胶垫厚度
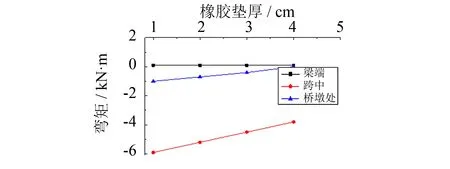
图11 主梁弯矩与橡胶垫厚度的关系Fig.11 Relationship between bending moment and rubber pad thickness
本桥采用橡胶垫代替支座来支撑上部结构, 为了解橡胶垫对主梁弯矩的影响, 考虑改变橡胶垫厚度分析主梁的弯矩变化, 如图11所示. 由图11可看出, 橡胶垫厚度改变时, 端部、 跨中和桥墩处主梁弯矩略有增加, 端部弯矩增量小于跨中和桥墩处弯矩增量, 但增幅较小, 可忽略不计. 由于没有改变橡胶垫支撑位置, 橡胶垫厚度改变时, 对台、 墩下部结构受力没有影响.
5 结语
1) 主梁与桥台的连接方式对整体桥受力的影响大于主梁与桥墩处的连接方式.
2) 主梁与桥台刚接时, 在整体温度变化作用下, 结构内产生的附加轴力远大于主梁与桥台采用半刚接的. 实桥算例中前者为后者的2.74倍.
3) 对于采用钢棒连接的半刚性节点, 参数分析表明, 橡胶套壁厚是影响主梁弯矩的主要因素, 橡胶垫及钢棒直径对主梁弯矩影响较小; 橡胶套和钢棒直径对桥台处柱-桩基的影响较大, 对桥墩处柱-桩基受力可忽略不计, 橡胶垫厚度对下部结构受力没有影响.

