Hilbert空间中K-框架的构造

杜丹丹, 朱玉灿

(福州大学数学与计算机科学学院, 福建 福州 350108)

0 引言

Hilbert空间中的框架是标准正交基的一种推广, 框架的一些性质和标准正交基类似, 但是也有明显的区别. 比如: Hilbert空间中的元素用框架展开的表达式是不唯一的, 而用标准正交基展开的表达式是唯一的, 因此框架和标准正交基本质上是不同的, 从而研究框架的性质是很有必要的. 国内外相关学者对框架理论进行系统研究, 具体成果可参见文献[1-2]. 框架在诸如采样理论[3]、 压缩感知[4]等应用领域也起着重要的作用.

文献[5]在Hilbert空间中研究有界线性算子时引入了一种称之为K-框架的推广框架.K-框架与框架本质上并不相同, 文献[5]证明了序列{fj}j∈J为H的K-框架当且仅当{fj}j∈J为H的Bessel序列且其合成算子Tf满足R(K)⊂R(Tf), 而序列{fj}j∈J为H的框架当且仅当{fj}j∈J为H的Bessel序列且其合成算子Tf为满射. 正是因为K-框架与框架之间存在的差异性, 国内外众多学者开始对其进行研究, 并且已经取得了一系列成果[6-9].

构造框架这一问题有很多学者已经进行研究, 比如文献[2]用已有的框架经过有界线性算子扰动构造新的框架, 文献[10]用一个框架和一个Bessel序列构造框架, 在此基础上, 文献[11]采用强分离性框架的概念给出了构造框架的另外一种方法. 在K-框架概念被提出后, 许多学者开始思考是否构造框架的相关结论仍然适用于构造K-框架, 比如文献[8-9]已讨论了用两个K-框架构造K-框架的方法. 本研究在此基础上讨论用两个Bessel序列构造K-框架的方法, 当取K为恒等算子时, 可得到构造框架的相关结论. 文献[7]中已经指出一个框架经算子K扰动后是K-框架, 那么K-框架经有界线性算子T1扰动后是否是T1-框架? 本研究讨论更加一般的情形, 即用两个Bessel序列构造T1-框架或T2-框架. 最后， 将用两个K-框架构造P-框架或Q-框架.

1 预备知识

定义1[2]设序列{fj}j∈J⊂H, 若存在正数A和B使得对于∀f∈H, 有：

则称{fj}j∈J为H的框架, 其中A和B分别称为框架的下界和上界. 若只有右边的不等式成立, 则称序列{fj}j∈J为H的Bessel序列, 并且可以定义有界线性算子Tf如下：

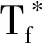
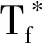
定义2[5]设序列{fj}j∈J⊂H, 若存在正数A和B使得对于∀f∈H, 有：

则称{fj}j∈J为H的K-框架, 其中A和B分别称为K-框架的下界和上界. 特别地, 当K=I时,K-框架就是通常的框架.

2 主要内容及结论

为了证明主要结论， 先给出两个引理.

引理1[2]设H1,H2是两个复Hilbert空间,T:H1→H2是具有闭值域的有界线性算子, 则存在唯一的算子T+:H2→H1满足：

称算子T+为T的伪逆算子.

引理2[6]设H1,H2是两个复Hilbert空间,T:H1→H2是具有闭值域的有界线性算子, 则

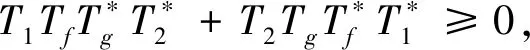
则{T1fj+T2gj}j∈J是H2的K2-框架, 其框架算子为：

证明 因为{fj}j∈J和{gj}j∈J是H1的Bessel序列, 不妨设其界分别为B1和B2, 所以对于∀f∈H1, 有

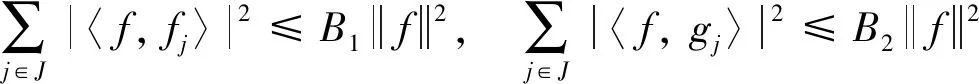
由闵可夫斯基不等式可知, 对于∀g∈H2, 有：

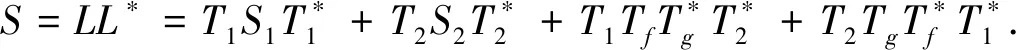
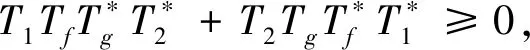
假设条件1)成立, 设{fj}j∈J为H1的K1-框架, 其下界为A1, 由引理2 可知， 对于∀g∈H2有：

综上所述序列{T1fj+T2gj}j∈J是H2的K2-框架.

同理可证当满足条件2)时，结论也是成立的.并且其框架算子为：

证毕.

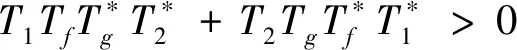
Kf=〈f,e1〉e1+〈f,e3〉e2

注1由定理1可推出文献[2]的推论5.32和文献[12]的定理3.3, 可改进文献[8]的定理4.1、 文献[9]的定理2.12、 文献[10]的定理3.2以及文献[11]的定理2.1.

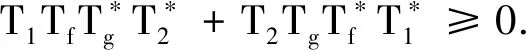
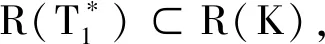
证明 满足条件时, 根据定理1的证明得{T1fj+T2gj}j∈J是H的Bessel序列, 且对于∀f∈H, 有

当满足条件I)时, 设{fj}j∈J是H的K-框架, 其下界为A1, 则由引理2可知， 对于∀f∈H, 有：

则{T1fj+T2gj}j∈J是H的T1-框架. 同理可证当满足条件II)时， {T1fj+T2gj}j∈J是H的T2-框架. 证毕.

下面通过具体例子, 说明存在不满足定理1的条件但满足定理2的条件并且为T2-框架的序列{T1fj+T2gj}j∈J.

K:H→H,Kf=〈f,e1〉e1+〈f,e3〉e2+〈f,e2〉e3(f∈H)

注2由定理2可推出文献[7]的命题3.6, 可改进文献[10]的定理3.2.

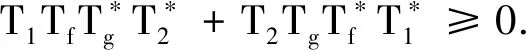
① 若K具有闭值域,P=T1+T2且R(P*)⊂R(K), 则{T1fj+T2gj}j∈J是H的P-框架.

② 若K具有闭值域,Q=T1-T2且R(Q*)⊂R(K), 则{T1fj+T2gj}j∈J是H的Q-框架.

证明 若满足条件, 设{fj}j∈J和{gj}j∈J的K-框架, 其下界分别为A1和A2. 根据定理1的证明过程, 可知{T1fj+T2gj}j∈J是H的Bessel序列, 且对于∀f∈H, 有：

当满足条件①时, 取λ=min{A1,A2}, 由内积空间中平行四边形公式和引理2, 得对于∀f∈H, 有：

从而{T1fj+T2gj}j∈J是H的P-框架. 同理可证当满足条件②时, {T1fj+T2gj}j∈J是H的Q-框架. 证毕.

注3由定理3可推出文献[7]的命题3.6. 下面举例说明定理2条件不蕴含定理3条件.

K:H→H,Kf=〈f,e1〉e1+〈f,e2〉e3(f∈H)