一道简单的不等式及其应用——兼答有奖解题擂台(122)和一道奥赛题

福建省福州市福州第二十四中学 (邮编：350015)

本文先给出并证明一道简单的不等式，然后举例说明其应用.为此，我们将这个不等式作为定理给出.

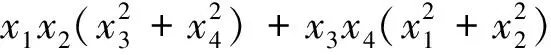
当且仅当x1=x2或x3=x4时取等号.

即得原式，易知当且仅当x1=x2或x3=x4时,取等号.

下面举一些例子，说明定理中的不等式的应用.在定理中不等式的右边应用均值不等式，便得到

例1 (自创题，2017.08.17)设x1、x2、x3、x4∈R，则

当且仅当x1=x2=x3=x4时取等号.

作为定理中的不等式的特例，有

例2 设x、y∈R，则8xy(x2+y2)≤(x+y)4.

利用例2中的结论，可得到以下

例3 设xi≥0，i=1,2,…,2n，则

(x1+x2)(x3+x4)…(x2n-1+x2n)≥

当且仅当x1=x2,x3=x4,…，x2n-1=x2n时,取等号.

证明先证明以下

引理设ai≥0，i=1,2,3,4,5,6，则

(根据以上例2不等式8xy(x2+y2)≤(x+y)4，其中x、y为任意实数)，即得原式.

下面证明原式.

根据以上不等式，有

即

同理可得类似的19个不等式，将这20个不等式左右两边分别相加，得到

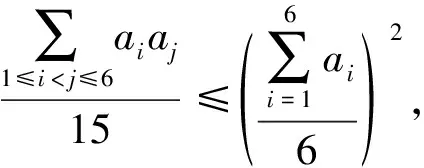
故原式获证.

例5 (自创题，2009.02.03)设a、b、c、d∈R+，且a+b+c+d=4，则

当且仅当a=b=c=d=1时,取等号.

证明例5中的不等式等价于

(a+b)(c+d)(a+b+c+d)4≥16abcd(a2+b2+c2+d2).

(※)

由于16abcd(a2+b2+c2+d2)=16abcd(a2+b2)+16abcd(c2+d2)

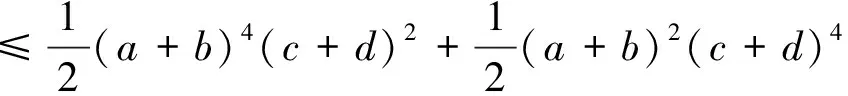
即得式(※)，故例5获证，易知当且仅当a=b=c=d=1时,取等号.

在例5中的左边应用均值不等式，得到

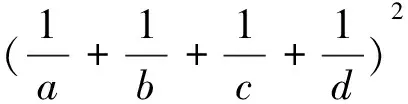
≥4(a2+b2+c2+d2).

当且仅当a=b=c=d=1时取等号.

例7 (自创题，2017.08.17)设a、b、c、d∈R+，则

(a+b)2(b+c)(c+d)2(d+a)≥4abcd(a+b+c+d_)2，

当且仅当a=b,c=d时取等号.

证明由定理可知，只要证明

(b+c)(d+a)·4[ab(c+d)2+cd(c+d)2]≥4abcd(a+b+c+d)2，

≥(b+c-d-a)2，

中药复方发挥药效的物质基础是有效化合物群，包含多种活性成分，其治疗是一个整体协调的过程[15-16]。指纹图谱技术可全面反映中药化学成分的种类与数量，中药指纹图谱目前已成为国际上公认的控制天然药物质量的有效手段[17]。本研究采用RP-HPLC法对10批护肝剂进行指纹图谱研究及化学模式识别，并对该制剂中马钱素、芍药苷、野黄芩苷、黄芩苷、黄芩素、五味子甲素、五味子乙素、五味子丙素和熊果酸9种活性成分进行了定量测定，为护肝剂的质量控制提供了科学依据。

≥(b+c-d-a)2.

由柯西不等式知上式成立，故原命题获证.

由证明过程中易知，当且仅当a=b,c=d时取等号.

由例6可以证明《中学数学教学》(安徽)2019年第2期刊登的赵忠华老师提出的有奖解题擂台(122)，即以下

例8 设a、b、c、d>0，且abcd=1，证明：

证明应用例5中的不等式得到

(a+b)2(b+c)(c+d)2(d+a)≥4abcd(a+b+c+d)2，

(a+b)(b+c)2(c+d)(d+a)2≥4abcd(a+b+c+d)2，

(a+b)(b+c)(c+d)(d+a)

因此，要证明原命题，只要证明

即27(a+b+c+d)4

≥256(a+b+c+d-1)3.

(※※)

设a+b+c+d=s≥4，则

27(a+b+c+d)4-256(a+b+c+d-1)3

=27s4-256(s-1)3

=(s-4)2(27s2-40s+16)

故式(※※)成立，例8获证.

例9 设a、b、c、d≥0，则

(ab+cd)[(a+b)2(c+d)2+16abcd]≥4abcd(a+b+c+d)2，

当且仅当a=b=c=d时取等号.

证明根据定理中的结论，有

(a+b)2(c+d)2≥4ab(c2+d2)+4cd(a2+b2)，于是，只要证明

(ab+cd)[4ab(c2+d2)+4cd(a2+b2)+16abcd]≥4abcd(a+b+c+d)2，

⟺(cd+ab)[ab(c+d)2+cd(a+b)2]≥abcd(a+b+c+d)2，

上式由柯西不等式即得证明，例9获证，从证明过程可知，当且仅当a=b=c=d时取等号.

由例9可得

例10 设a、b、c、d≥0，则

(a+b)2(c+d)2(ab+cd)

≥4abcd(a+b+c+d)2，

当且仅当a=b=c=d时取等号.

证明在例9中注意到

(a+b)2(c+d)2≥16abcd，即得.

例11 设a、b、c、d≥0，则

(a+b)(c+d)(ab+cd)[(a+b)2+(c+d)2]≥16abcd∑a2，

当且仅当a=b=c=d时取等号.

根据定理中的不等式可知，只要证明

(ab+cd)[(a+b)2+(c+d)2]

≥16abcd∑a2，

⟺(ab+cd)[ab(c2+d2)+cd(a2+b2)][(a+b)2+(c+d)2]

≥4abcd(a+b)(c+d)∑a2，

⟺(ab+cd)[ab(c+d)2+cd(a+b)2-4abcd][(a+b)2+(c+d)2]

≥4abcd(a+b)(c+d)[(a+b)2+(c+d)2-2(ab+cd)]，

⟺(ab+cd)[ab(c+d)2+cd(a+b)2] [(a+b)2+(c+d)2]

-4abcd(ab+cd)[(a+b)2+(c+d)2]

≥4abcd(a+b)(c+d)[(a+b)2+(c+d)2]

-8abcd(ab+cd)(a+b)(c+d)，

⟺[a2b2(c+d)2+c2d2(a+b)2][(a+b)2+(c+d)2]

+abcd[(a+b)2+(c+d)2]2

-4abcd(ab+cd)[(a+b)2+(c+d)2]

≥4abcd(a+b)(c+d)[(a+b)2+(c+d)2]

-8abcd(ab+cd)(a+b)(c+d)，

⟺[a2b2(c+d)2+c2d2(a+b)2][(a+b)2+(c+d)2]

-2abcd(a+b)(c+d)[(a+b)2+(c+d)2]

+abcd[(a+b)2+(c+d)2]2-2abcd(a+b)(c+d)[(a+b)2+(c+d)2]

≥4abcd(ab+cd)[(a+b)2+(c+d)2]

-8abcd(ab+cd)(a+b)(c+d)，

⟺[(a+b)2+(c+d)2][ab(c+d)-cd(a+b)]2

+abcd[(a+b)2+(c+d)2](a+b-c-d)2

≥4abcd(ab+cd)(a+b-c-d)2，

⟺[(a+b)2+(c+d)2][ab(c+d)-cd(a+b)]2

+abcd[(a-b)2+(c-d)2](a+b-c-d)2≥0，

上式显然成立，故原命题获证，易知当且仅当a=b=c=d时取等号.

应用例11 中的不等式，可以证明以下