三维箱体收敛于二维水动力学特性影响因素的研究

薛继阳 熊鳌魁

(武汉理工大学交通学院 武汉 430063)

0 引 言

尽管海上结构物所受的环境载荷比较复杂,但对其的水动力学特性的研究也越来越深入.要准确的预判箱体在波浪中的运动性能,附加质量,阻尼等都必须得到准确的计算.但是对于一些超大型浮体的水动力分析,在三维情况下的计算比较复杂而且耗时较长,如果其水动力特性能采用基于二维思想的细长体假设或切片理论进行计算分析,则其计算过程相对方便简洁且计算速度要比三维的快.

切片理论的发展逐渐成熟且被广泛的应用于水动力系数,波载和运动响应的评估,有关学者基于切片理论已作出了一些研究.文献[1]的水动力计算便基于切片理论在频域范围内对40万吨超大型矿砂船CHINAMAX的耐波性进行了分析,得出了船舶运动以及附加阻尼力等响应变量的传递,进而对运动响应进行短期预报.文献[2]基于切片理论,以某一工程船型为例,对其波浪载荷直接计算并将计算结果与规范值进行比较,通过非线性化修正,从而来模拟实际波浪载荷的非线性效应.文献[3]以某300 t级执法船为例,基于二维切片理论和三维势流理论方法,采用谱分析法对耐波性进行了短期预报并与船模试验结果进行了比较,得到相应的结论.文献[4]基于STF切片理论对狭窄航道中低速船舶的纵向运动进行预报并进一步分析不同水深和不同航道半宽对船舶附加质量和阻尼系数的影响.文献[5]应用切片理论,以双椭球体辐射问题为例进行了流体动力系数的计算,与三维源汇分布法结果的比较表明,改进后的切片法可有效地抑制伪共振现象,从而可用于双体船在波浪中运动响应计算. 文献[6]运用细长体理论,研究了两个细长的回转体之间的高阶水动力相互作用的影响.结果表明，对于较大的横向分离距离来说,高阶力的影响是相对较小的,对于小的分离距离来说影响较大.文献[7-8]研究了两个细长体的水动力相互作用(包括侧向力和偏航力矩)，并利用匹配的渐近展开和正形映射来进行求解.文中基于水动力学软件AQWA研究了系列长度,宽度和水深对箱体水动力特性的影响情况,并将其三维结果(这里指单位长度的结果)与对应的二维级数解进行比较,探讨了箱体尺寸和水深对水动力学参数收敛情况的影响.

1 环境条件和箱体建模

由于计算的工况较多,故这里只说明基础工况的环境条件和箱体参数,其他工况的参数在分析图中可查阅.箱体的尺寸为L×W×H=1 m×1 m×0.5 m.水文参数如下:水的密度为1 025 kg/m3,波高为0.2 m,水深为0.6 m,吃水为0.25 m,波浪方向为90°,角频率为0.3～11 rad/s.

2 算例分析与结果比较

2.1 附加质量的分析

通过水动力学软件AQWA对不同工况下的附加质量和二维附加质量进行计算,见图1～6.

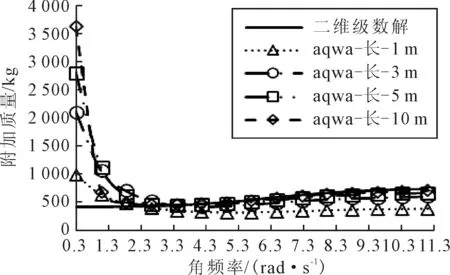
图1 水深0.6 m,宽1 m,升沉引起的附加质量

由图1可知,对于水深0.6 m、宽1 m的工况而言,当频率较小时,箱体的长度越长,由升沉引起的附加质量的大小(这里指单位长度的值)偏离二维级数解的程度越大,出现这种现象有可能是计算的频率接近临界值而造成的问题,随着频率的增加,附加质量逐渐向二维级数解靠拢并趋向于收敛.当频率达到一定值时,随着长度的增加,附加质量逐渐增大并向二维级数解收敛,达到稳定时,长为1 m的附加质量与二维的情况存在一定的偏差,小于二维解.长为10 m的附加质量和二维级数解重合,已完全收敛.

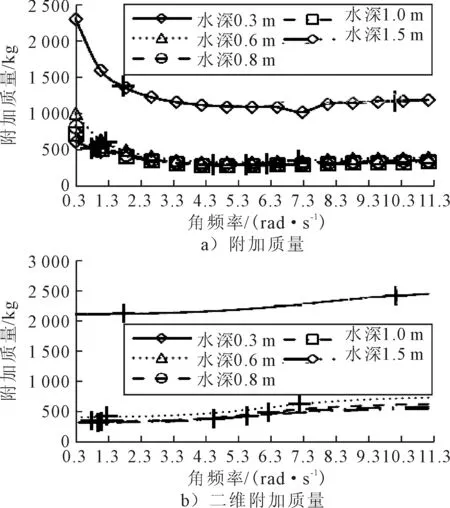
图2 长1 m,宽1 m,升沉引起的附加和二维附加质量

保持箱体的长和宽不变,由图2可知,附加质量随水深的增加而单调减少,跟二维的变化规律保持一致.对于同一水深,当水深较深,频率较高时,由aqwa计算的附加质量和二维计算的附加质量吻合效果较好,即已达到收敛.说明各水深情况都应该类似于0.3和0.6 m水深的情况,从对应的二维曲线以相同的方式收敛于二维级数解.

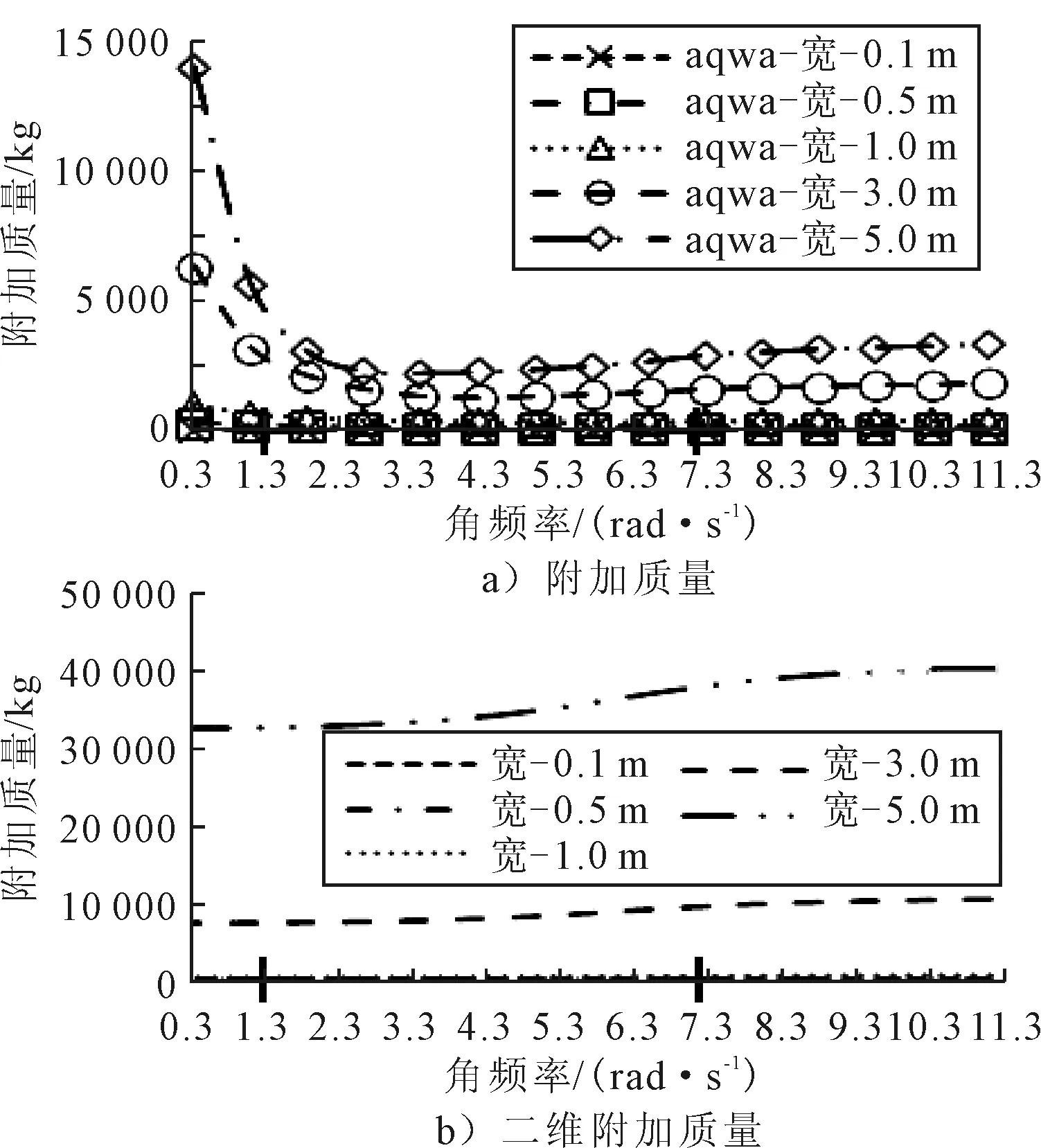
图3 水深0.6 m、长1 m,升沉引起的附加和二维附加质量

保持箱体长度为1 m和水深为0.6 m不变,由图3可知,附加质量随宽度的增加而单调增加,对于同一宽度,宽度较小时,附加质量的增长率很小,这与二维的变化规律保持一致,但3 m以上宽度的波动幅度较明显.这种波动曲线在一定频率范围内还是有收敛到二维曲线的趋势,但收敛缓慢.

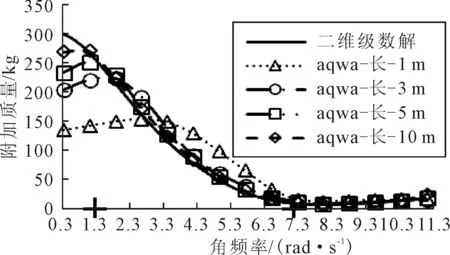
图4 水深0.6 m,宽1 m,横荡引起的附加质量

由图4可知,对于水深0.6 m、宽1 m的工况而言,在低频时,结构长度越长,由横荡引起的附加质量(这里指单位长度的值)越大,逐渐向二维级数解收敛,随着频率的增加,其附加质量值超越二维解然后下降并向二维级数解收敛,当角频率大约大于8.3 rad/s时,附加质量几乎不再随长度的变化而改变,完全收敛于二维级数解.

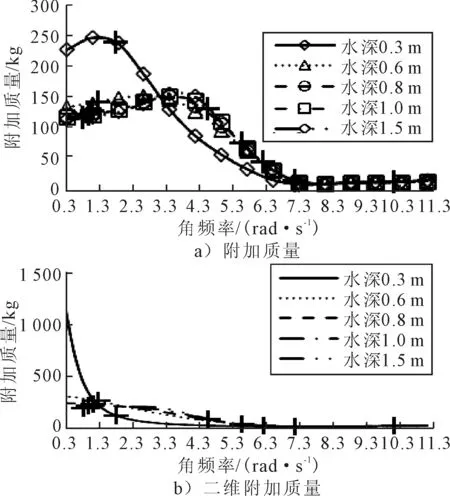
图5 长1 m、宽1 m,横荡引起的附加和二维附加质量

保持箱体的长和宽不变,由图5可知,对于不同的频率，附加质量随着水深的变化规律不同.当角频率大于8.3 rad/s时,附加质量几乎不随水深的变化而变化.尽管按常规定义,对于低频的波仍属于有限水深或浅水,其中波的类型在图中以“+”的形式标出.而在二维情况下略有所不同,主要在于附加质量的变化规律发生改变时所对应的角频率值不同和用aqwa计算出来的附加质量的幅值不同于二维级数解的幅值,说明各水深情况都应该类似于0.3和0.6 m水深的情况,从对应的二维曲线以相同的方式收敛于二维级数解.

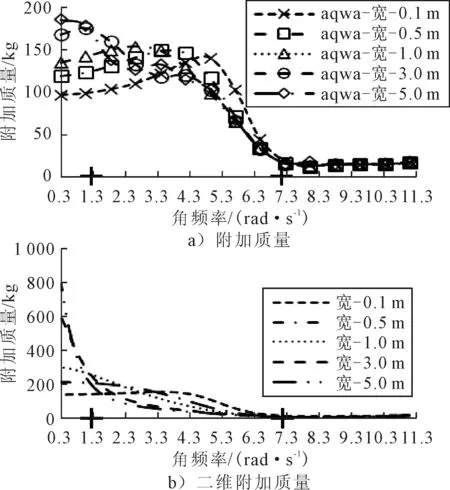
图6 水深0.6 m、长1 m,横荡引起的附加和二维附加质量

保持箱体的长和水深不变,由图6可知,频率不同时，附加质量随着宽度的变化规律不同.对应的二维附加质量有相似的现象,比如，当角频率较高时同样呈现收敛的趋势.但3 m以上宽度的相对波动幅度比较明显,因此通过加算,这种波动曲线随长度的增加逐渐向二维曲线收敛.

2.2 阻尼的分析

通过水动力学软件AQWA对不同工况下的阻尼和二维阻尼进行计算,见图7～12.

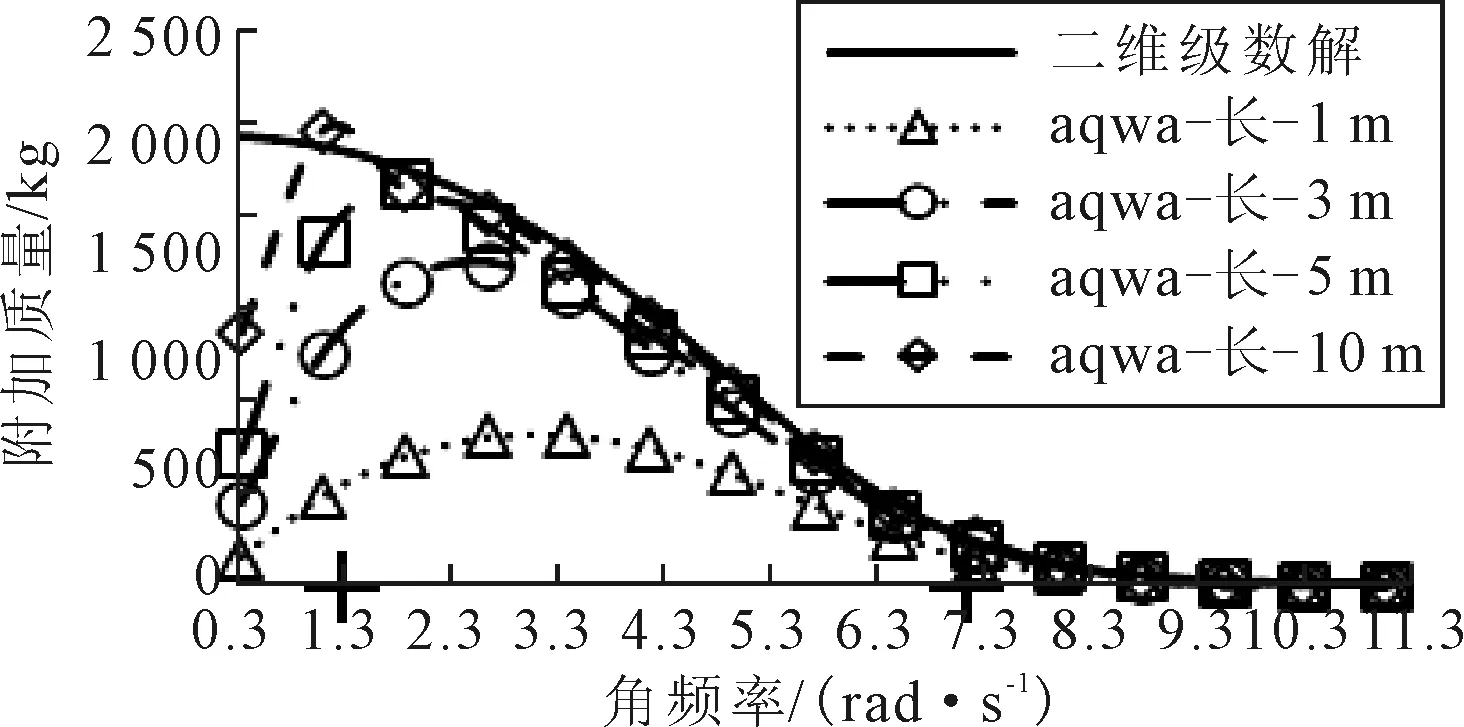
图7 水深0.6 m、宽1 m,升沉引起的阻尼

由图7可知,对于水深0.6 m宽1 m的工况而言,当频率较小时,箱体的长度越长,由升沉引起的阻尼(这里指单位长度的值)越大,即偏离二维级数解的程度越小,随着角频率的增加,长度越长,阻尼越大且逐渐向二维级数解靠拢并趋向于收敛,其中,长度越长向二维解收敛的速度越快.当角频率大于8.3 rad/s时,阻尼以完全收敛,不再随长度的变化而变化.

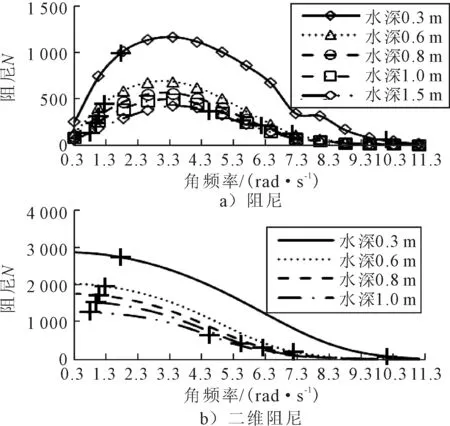
图8 长1 m、宽1 m,升沉引起的阻尼和二维阻尼

保持箱体长和宽不变,由图8可知,阻尼随水深的增加而单调减少,跟二维的变化规律基本一致,当频率达到一定值时,阻尼几乎不再随水深的变化而改变,尽管按常规定义,对于低频的波仍属于有限水深或浅水,其中波的类型在图中以“+”的形式标出.但二维级数解的值都大于由aqwa计算出来的阻尼值.说明各水深情况都应该类似于0.3和0.6 m水深的情况,从对应二维曲线的下方,以相同的方式收敛于二维级数解.

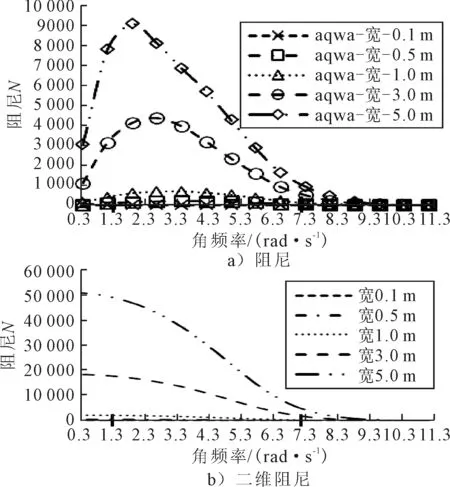
图9 水深0.6 m、长1 m,升沉引起的阻尼和二维阻尼

保持箱体长度为1 m和水深为0.6 m不变,由图9可知,阻尼随宽度的增加而单调增加,当宽度较小时,阻尼的增长率很小,对应的二维阻尼有相似的现象,但二维级数解的值都大于由aqwa计算出来的阻尼值.但3 m以上宽度的相对波动幅度比较大,且3和5 m宽度的曲线没有交织在一起.这种波动曲线在低频时还是有收敛到二维曲线的趋势,但收敛缓慢.

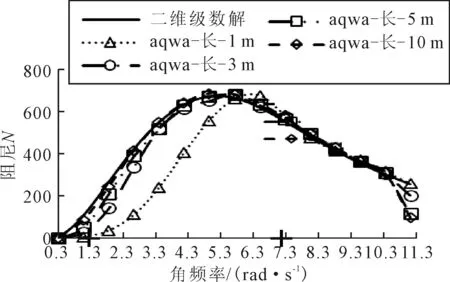
图10 水深0.6 m、宽1 m,横荡引起的阻尼

由图10可知,对于水深0.6 m宽1 m的工况而言,随着箱体长度的增加,由横荡引起的阻尼(这里指单位长度的值)单调增加并逐渐向二维级数解收敛.当频率大于5.7 rad/s时,阻尼超越二维解然后下降并向二维解收敛,随着频率的增加,阻尼几乎不随长度的增加而变化,都收敛于二维级数解.但当角频率为10.3 rad/s时,除了1 m的工况其余工况都出现了发散的情况,其阻尼偏离了二维级数解.

图11 长1 m、宽1 m,横荡引起的阻尼和二维阻尼

保持箱体的长和宽不变,由图11可知,在频率小于5.5 rad/s时,阻尼随着水深的增加而单调减小,在角频率5.5 rad/s<ω<8 rad/s,阻尼的变化规律发生改变,随着水深的增加逐渐增加,当角频率大于8 rad/s时,阻尼达到稳定状态,几乎不随水深的变化而变化.尽管按常规定义,对于低频的波仍属于有限水深或浅水,其中波的类型在图中以“+”的形式标出.而在二维情况下有所不同,主要在于阻尼的分布情况发生改变时所对应的频率值不同和用aqwa计算出来的阻尼的幅值不同于二维级数解的幅值,说明各水深情况都应该类似于0.3和0.6 m水深的情况,从对应的二维曲线以相同的方式收敛于二维级数解.

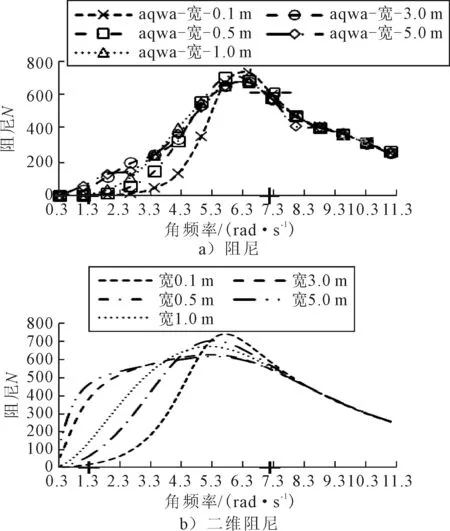
图12 水深0.6 m、长1 m,横荡引起的阻尼和二维阻尼

保持箱体的长和水深不变,由图12可知,在频率较小时,阻尼随着宽度的增加大体呈现增加的趋势,但是有反常的情况出现,随着频率的增加,阻尼发生变化,随着宽度的增加逐渐减小最后达到稳定状态,几乎不随宽度的变化而变化.在二维情况下,当宽度较小时,两者的变化规律大体一致,尤其在高频时已完全收敛.当频率较低时,对于宽为5 m的工况,其阻尼曲线和二维曲线的差异较大，因此，通过加算,这种波动曲线随长度的增加逐渐向二维曲线收敛.

3 结 论

1) 对于由横荡引起的阻尼,当宽为1 m时,随长度的增加,其值在高频区出现偏差的现象.

2) 保持箱体宽度和水深不变时,随着长度的增加,在低频区由升沉引起的附加质量的值偏离二维解的程度越大，即有发散的趋势.

3) 保持箱体尺寸不变,随水深的增加,由升沉引起的附加质量和阻尼单调减少,其他物理量并非单调变化.

4) 保持水深和箱体长度不变,受宽度的影响,其对应的附加质量和阻尼与二维级数解的收敛性呈现出不同的现象.比如，在角频率较小时,由横荡引起的阻尼随着宽度的增加而增加,随着频率的增加,其值超越二维解然后下降向二维级数解收敛.