氯盐侵蚀环境下RC结构退化的细观模拟方法及其耐久性评估*

段瑞芳 乔星昇 白云腾

(陕西交通职业技术学院1) 西安 710018) (西安市政设计研究院有限公司2) 西安 710064)(旧桥检测与加固技术交通行业重点实验室3) 西安 710064)

0 引 言

结构的耐久性是材料抵抗自身和自然环境双重因素长期破坏作用的能力[1].影响耐久性的因素有：钢筋锈蚀、氯离子侵蚀、混凝土碳化等，其中氯离子的过度侵蚀会对钢筋混凝土结构的耐久性产生严重的破坏.氯离子侵蚀导致的钢筋锈蚀会引起钢筋混凝土结构的耐久性问题.我国海岸线漫长，氯离子侵蚀环境中的钢筋混凝土结构中，钢筋锈蚀引起的耐久性问题的严重程度不低于澳大利亚、美国等国家[2].该问题若被忽视，将会带来巨大的经济损失，因此，氯离子侵蚀环境下钢筋混凝土结构的耐久性研究具有很高的研究价值.

对于建筑结构而言，钢筋与混凝土的耐久性直接决定了整个建筑结构的耐久性.目前，Collepardi等[3-6]进行了氯离子在混凝土中扩散行为的研究，都将混凝土近似看作是匀质材料.但是，现实中混凝土并非匀质材料，混凝土中的骨料及钢筋等材料相对于砂浆基质属于质密材料，并不能作为氯离子扩散介质.

卢木等[7-9]对氯离子侵蚀环境下混凝土结构服役寿命预测做的研究，主要考虑各种特殊的侵蚀环境以及边界条件对氯离子在混凝土中的扩散模型进行修正，并提出氯离子侵蚀环境中的钢筋混凝土结构耐久性寿命预测分析.但仍未考虑钢筋混凝土材料的非均匀特性.

文中考虑了钢筋混凝土本身的非匀质特性，从细观角度出发，对混凝土材料进行了相应的细观假设，在假设的基础上，对氯离子在混凝土中的扩散行为及结构耐久性进行研究.首先，建立了二级配混凝土随机骨料模型.然后，研究了骨料以及钢筋的存在对氯离子扩散过程的影响；在此基础上，研究了二维扩散情况下角部钢筋的锈蚀规律.在对模型分析时，引入骨料综合作用修正系数kag、钢筋阻滞作用修正系数ks，以及角部钢筋修正系数kcr.结合上述修正系数，得出基于细观模拟的耐久性评价模型，对处于氯离子侵蚀环境下的某RC空心板桥进行耐久性评价及使用寿命预测.

1 氯离子侵蚀过程细观模拟及规律

1.1 氯离子扩散模型建立

以往研究表明，混凝土中氯离子的扩散方式属于线性方式.现行对混凝土劣化行为的研究，研究尺度有宏观、细观和微观三种.

以往针对混凝土材料性能的研究基本都是在宏观尺度下开展的.但是，将混凝土视为匀质材料的宏观尺度模型并不能反应混凝土材料的随机性和非均匀性，不能真实刻画混凝土材料的劣化过程.此外，微观尺度下的研究过于精细、涉及到的不均匀因素过多，研究过程不易掌控.

为了在简化分析过程的同时兼顾混凝土材料的非匀质特性，文中选择以细观尺度展开分析，将混凝土简化为由砂浆基质、界面过渡区以及骨料组成的三相不均匀复合材料，将骨料近似看作圆形，建立混凝土随机骨料模型进行研究，模型见图1.

图1 混凝土细观尺度试件

1.2 有限元细观模型的分析方法

目前尚无专门模拟氯离子在混凝土中扩散行为的计算软件，不过基于Fick第二定律的氯离子扩散公式与热传导计算公式的形式完全相同，所以可以使用热传导模拟软件来对氯离子在混凝土中的扩散过程进行模拟.

Fick第二定律计算公式为

(1)

式中：ρ为氯离子质量浓度，kg/m3；t为时间，年；D为扩散系数，m2/年；x为深度，m.

热传递公式为

(2)

式中：θ为温度，℃；t为时间，h；k为热传导率，J/(m·℃)；ρ为密度，kg/m3；c为比热容，J/(kg·℃)；x为深度，m.

选用有限元计算软件ANSYS中的热分析模块对氯离子在混凝土中的扩散过程进数值模拟.

1.3 骨料对氯离子扩散行为的影响规律

骨料对氯离子扩散的阻滞作用见图2，氯离子浓度随时间的变化曲线见图3.

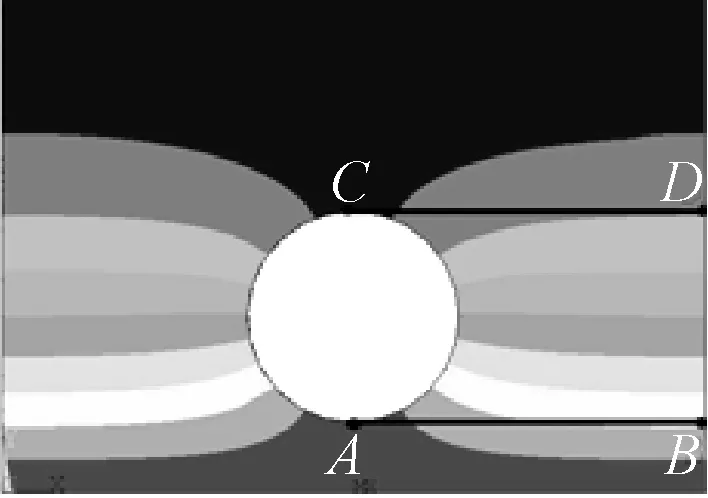
图2 骨料阻滞作用下 氯离子分布云图

图3 氯离子质量浓度 随时间变化曲线

由图2～3可知，考虑骨料的阻滞作用时，氯离子向混凝土内部扩散，并在骨料表面堆积，同一时刻骨料前沿点A点处的氯离子质量浓度比同一深度处B点处的高；同一时刻骨料前沿点C处的氯离子质量浓度比同一深度处D点处的低，且两者的差值ΔM随着时间推移会逐渐增大.骨料的阻滞作用对氯离子的扩散确实产生了一定的影响，但其影响范围仅限于骨料周围.

图4为不同骨料形状下混凝土试件氯离子质量浓度分布云图.不同深度处混凝土试件氯离子质量浓度分布见图5.

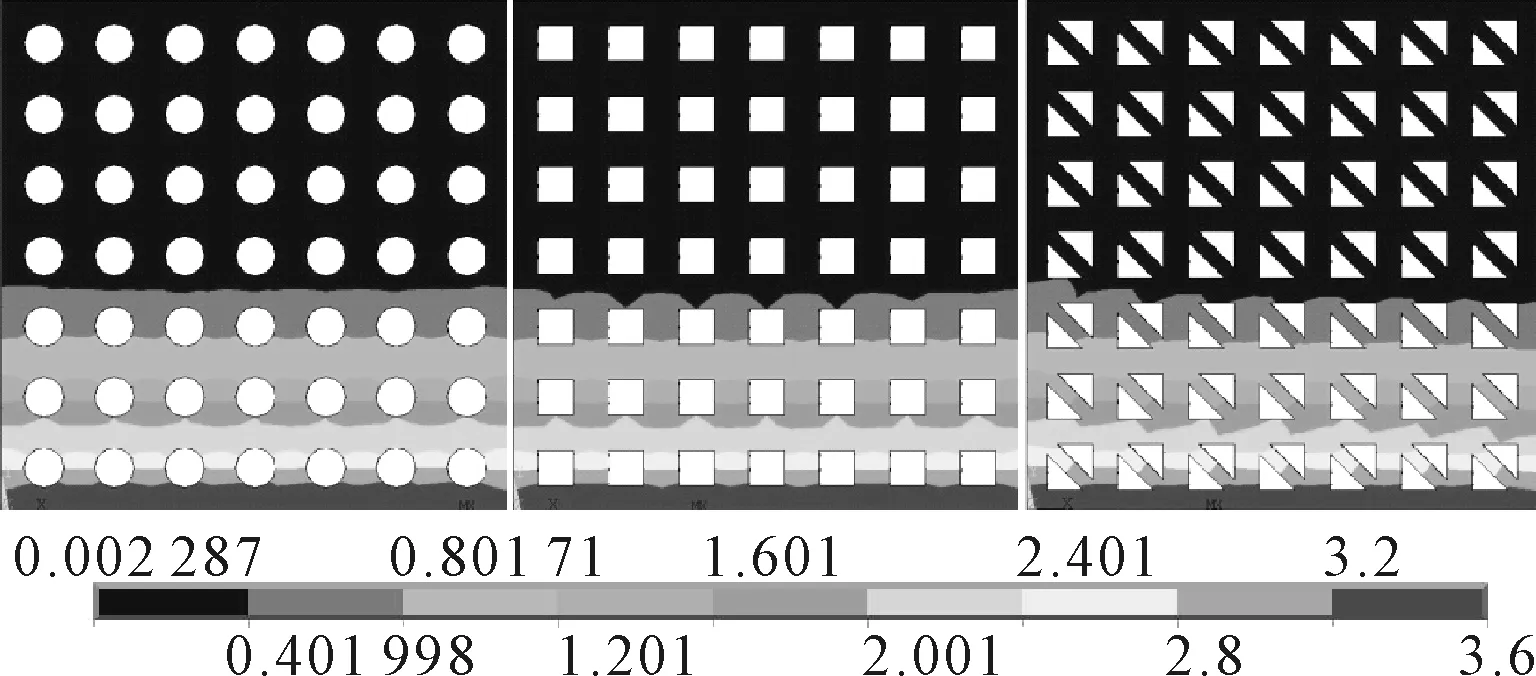
图4 不同骨料形状下混凝土试件氯离子质量浓度分布云图

图5 不同深度处混凝土试件氯离子质量浓度分布

由图4～5可知，骨料形状对氯离子在混凝土中的宏观扩散规律的影响基本可以忽略,因此,在进行数值模拟时可以将外表不规则的混凝土骨料简化为圆形骨料.

图6为不同骨料分布下混凝土中氯离子质量浓度分布云图，不同深度处混凝土试件氯离子浓度分布见图7.

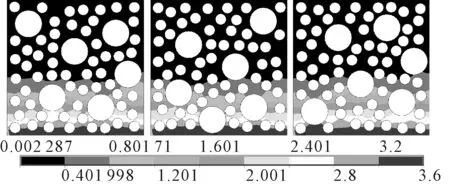
图6 不同骨料分布下混凝土中氯离子质量浓度分布云图

图7 不同深度处混凝土试件氯离子质量浓度分布

由图6～7可知，骨料的随机分布形式对混凝土中氯离子的宏观扩散规律不产生影响，因此，对氯离子在进行数值模拟时可以将随机分布的混凝土骨料简化为按一定规律排列的骨料.

图8中从左到右分别是体积分数为16%,32%,48%的RC结构在氯离子侵蚀环境中暴露20年后的氯离子空间分布云图.

由图8可知，体积分数越大，最大氯离子质量浓度等值线的高度越高，这说明骨料的体积效应加速了氯离子在混凝土内扩散的过程，而且骨料体积分数越大，这种加速效应越强.

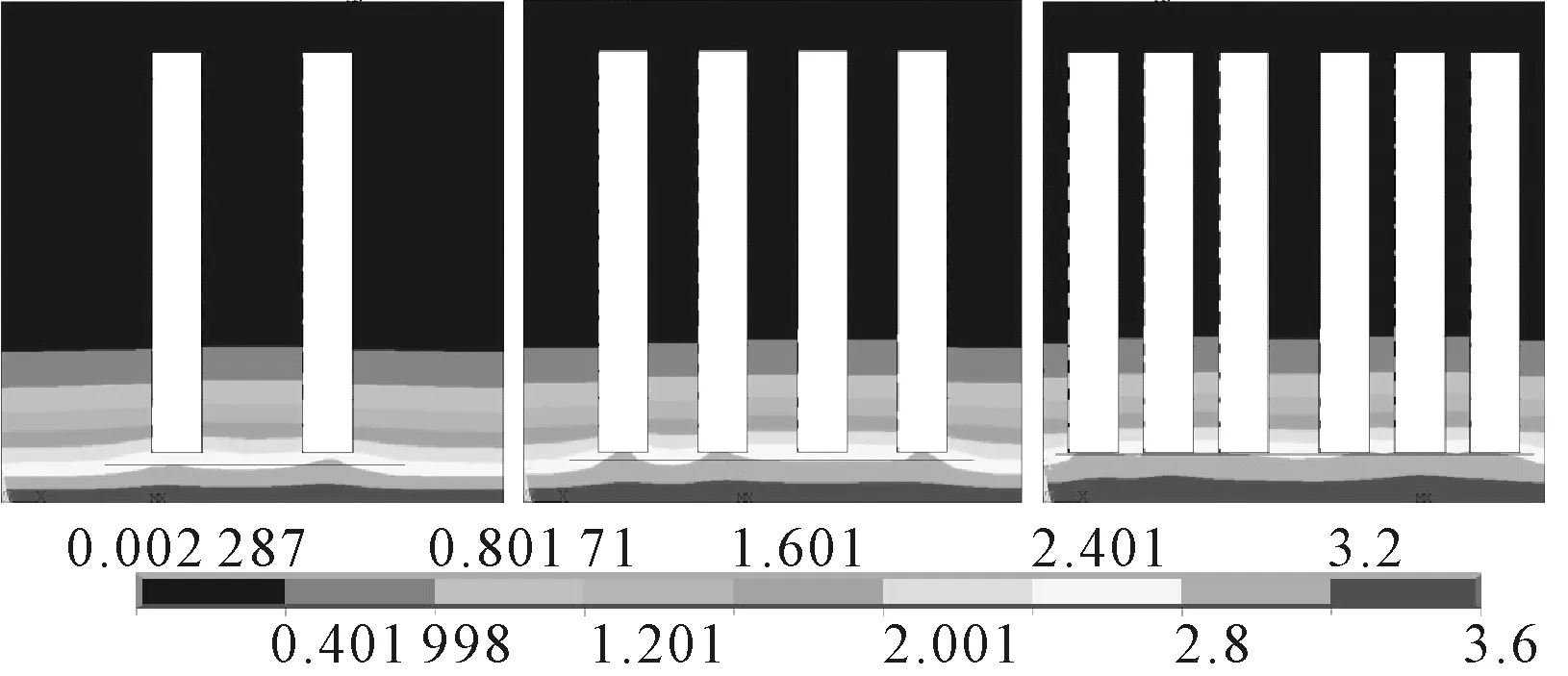
图8 不同骨料体积分数下氯离子质量浓度分布云图

此处选用骨料体积分数为46.9%的混凝土模型为研究对象，考虑骨料的阻滞作用与体积效应建立二级配混凝土随机骨料模型，分析骨料对氯离子扩散行为造成的综合影响规律.引入骨料总体效应对修正系数kag对不考虑骨料不透氯特性的耐久性预测模型进行修正.

t′=kag×t∶kag=t′/t

(3)

式中：t为不考虑骨料不透氯特性情况时钢筋的初锈时间,年；t′为考虑骨料不透氯特性情况时的钢筋初锈时间，年.

为了对kag进行赋值，对体积分数为46.9%的二级配混凝土随机骨料模型进行数值模拟，计算对比不同深度处钢筋的t与t′，结果见表1.

表1 氯离子浓度随混凝土保护层厚度变化统计表

通过对表1中的t′/t值进行数学统计，发现t′/t的平均数为0.916，这组统计数据的方差为1.388×10-6.所以对kag取值为0.916.

1.4 钢筋对氯离子扩散行为的影响规律

图9为钢筋阻滞作用下氯离子分布云图，氯离子质量浓度随时间变化曲线见图10.

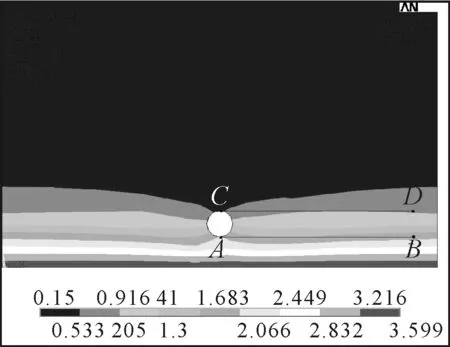
图9 钢筋阻滞作用下氯离子分布云图

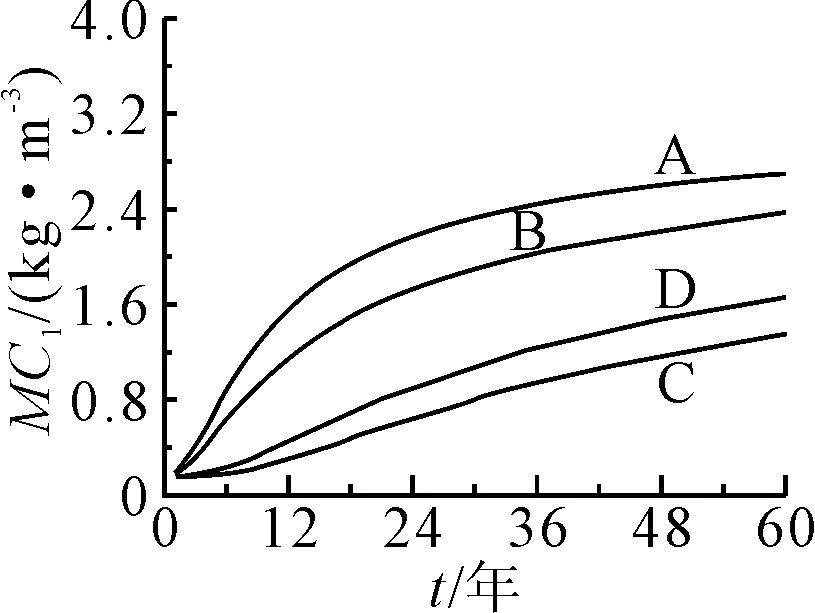
图10 氯离子浓度随时间变化曲线

由图9～10可知，考虑钢筋的阻滞作用后，钢筋前沿氯离子质量浓度上升速度加快，钢筋的阻滞作用会加速钢筋的锈蚀.钢筋直径为12 mm的混凝土保护层厚度对钢筋阻滞作用的影响见表2.

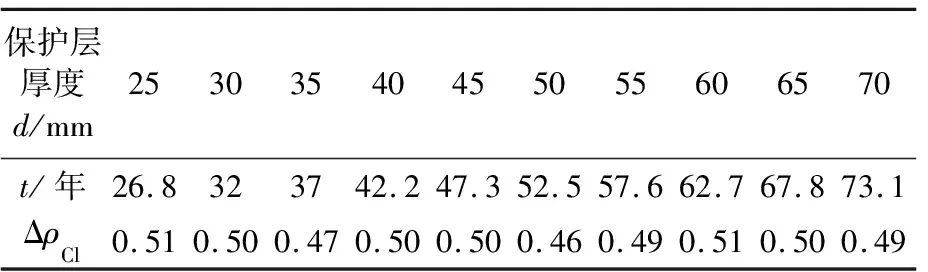
表2 混凝土保护层厚度对钢筋阻滞作用的影响(钢筋直径:12 mm)

由表2可知，在不同的混凝土保护层厚度的情况下，同直径的钢筋对氯离子传输的阻滞作用几乎不存在差异.但是保护层厚度的增大会使得扩散距离变长，钢筋初锈时间得以推迟，结构耐久性因此得到提高.这说明：实际中，增加混凝土保护层厚度是提高氯离子侵蚀环境下结构耐久性最直接的方法.

图11为不同钢筋直径的阻滞作用差异，氯离子浓度随时间变化曲线见图12.

图11 不同钢筋直径的 阻滞作用差异

图12 氯离子浓度随 时间变化曲线

由图11～12可知，钢筋直径越大，阻滞作用效果越显著，氯离子在钢筋前沿点处堆积速度越快，钢筋也就越早发生锈蚀，因此，得出结论：进行结构耐久性寿命设计时，在相同的截面尺寸及配筋率的前提下，相比于公称直径大、数量少的钢筋，选择公称直径小、数量多的钢筋能够有效提高结构耐久性.

因此，在对钢筋混凝土结构进行耐久性评价时，需要考虑钢筋的阻滞作用.此处引入钢筋阻滞作用修正系数ks对不考虑钢筋阻滞作用的耐久性预测模型进行修正.

(4)

式中：t1为不考虑钢筋不透氯特性情况下角部钢筋的初锈时间，年；t2为考虑钢筋不透氯特性情况下角部钢筋的初锈时间，年.

同时，对14～32 mm直径的钢筋进行计算分析，其他参数保持不变，以t2/t1的计算结果对考虑钢筋阻滞作用的修正系数ks进行赋值，见表3.

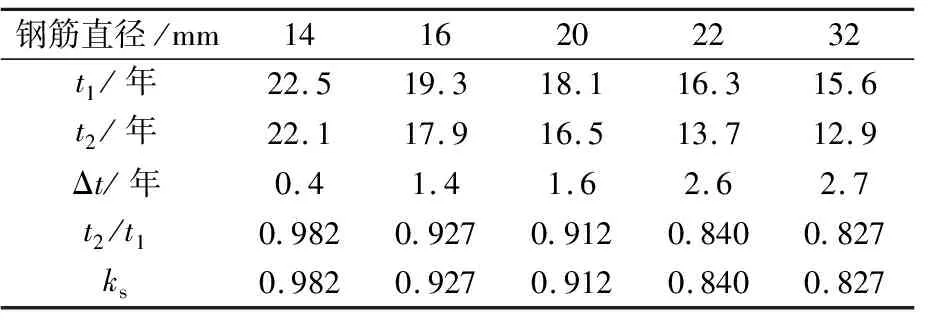
表3 钢筋阻滞作用修正系数取值

图13为一维、二维氯离子侵蚀环境中的氯离子空间分布云图，钢筋前沿点处氯离子浓度变化曲线见图14.

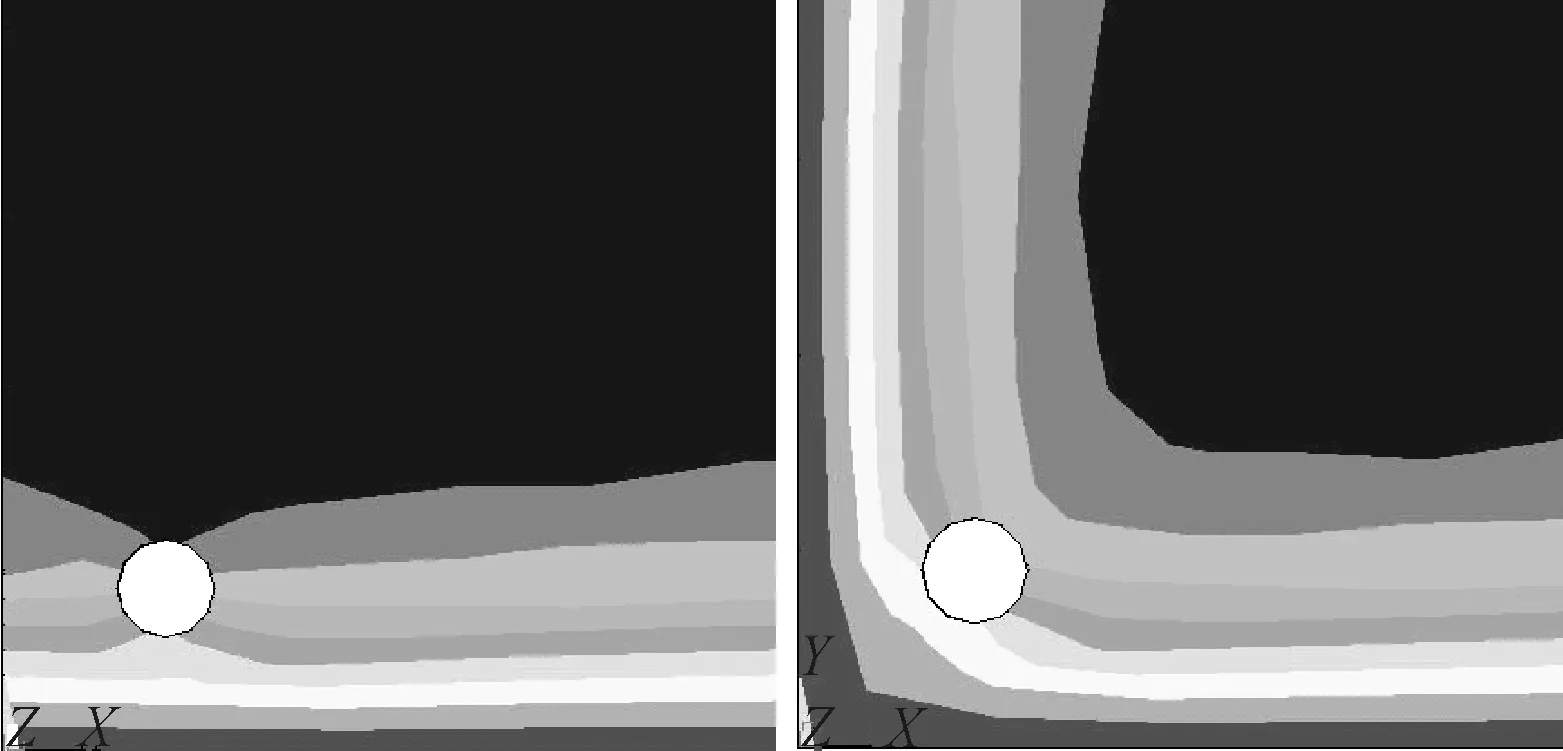
图13 一维、二维氯离子侵蚀环境中的氯离子空间分布云图

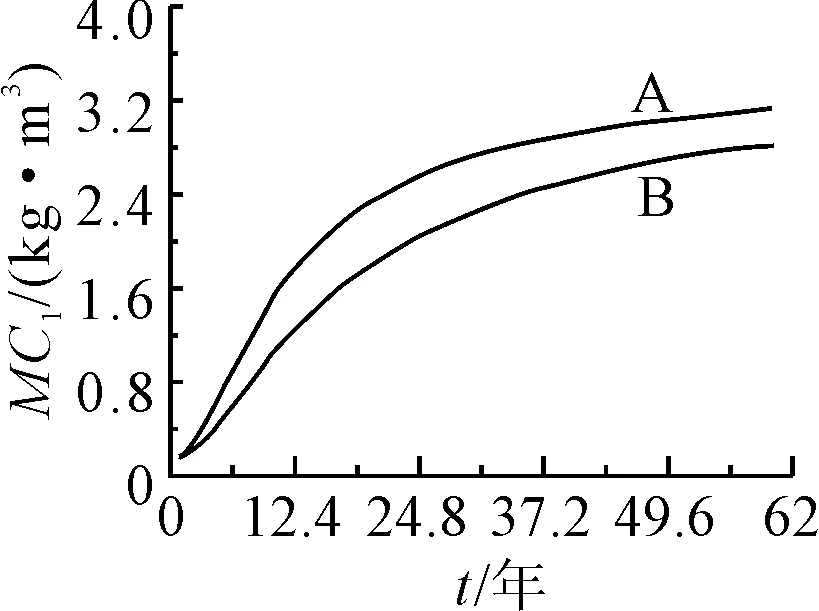
图14 一维、二维氯离子侵蚀环境中钢筋前沿点处氯离子浓度变化曲线

由图13～14可知，同条件下，钢筋锈蚀在二维扩散情况下要比一维扩散情况下的锈蚀速度快.因此在对结构进行耐久性评价或者耐久性设计时，必须考虑角部钢筋受到氯离子二维侵蚀的事实.

为了简化氯离子的扩散过程，同时兼顾角部钢筋的实际状况，引入角部钢筋修正系数kcr对二维扩散过程中角部钢筋初锈时间进行修正.

t2D=kcr×t1D∶kcr=t2D/t1D

(5)

式中：t1D为一维扩散环境下角部钢筋的初锈时间或锈胀开裂时间,年；t2D为二维扩散环境下角部钢筋的初锈时间或锈胀开裂时间,年.

通过计算，可以对kcr进行取值：若以钢筋初锈蚀时间作为耐久性极限状态，kcr取值为0.719；若以混凝土锈胀开裂时间作为耐久性极限状态，kcr取值为0.689.

2 基于可靠度的混凝土结构耐久性评价实用方法与应用

2.1 基于可靠度概念的耐久性寿命预测理论及方法

关于可靠度指标的基本计算方法有很多种，比如：均值一次二阶矩法、改进的一次二阶矩法和JC法等.

采用基于可靠度的随机概率预测法对氯离子侵蚀环境中的混凝土结构的耐久性进行评价，以钢筋开始发生锈蚀极限状态作为结构寿命的终点.

根据文献[10]，按氯离子结合机制的不同，混凝土结构在Langmuir、Fangmuir，以及线性结合机制下的寿命预测模型为

1) Langmuir结合机制下的寿命预测模型

(6)

2) Fangmuir结合机制下的寿命预测模型

(7)

3) 线性结合机制下的寿命预测模型

(8)

式中：ρCl-,cr为临界氯离子质量浓度，kg/m3；d为混凝土保护层厚度，mm；T为混凝土结构使用寿命，年；α为结合系数1；β为结合系数2；ρCl-,f为自由氯离子浓度；ρCl-,0为结合氯离子质量浓度；m为衰减系数；D0为t0时刻混凝土的氯离子扩散系数；erf-1为误差函数.

在保证计算精度的前提下，为了简化计算模型，选用线性结合机制下的寿命预测模型对结构进行耐久性评价及使用寿命预测.

2.2 考虑修正系数的线性结合机制下的寿命预测模型

对于线性结合机制下的寿命预测模型，应当考虑角部钢筋修正系数kcr、骨料综合作用修正系数kag、钢筋阻滞作用修正系数ks对模型进行修正，用修正后的模型对实例进行耐久性分析.由第二章的分析可得，kag取值为0.916；ks的取值随着钢筋直径的改变而发生改变，具体见表3；若以钢筋初锈蚀时间作为耐久性极限状态，kcr取值为0.719；若以混凝土锈胀开裂时间作为耐久性极限状态，kcr取值为0.689.

修正后的线性结合机制下的寿命预测模型

kcr·kag·ks

(9)

式中：kcr为角部钢筋修正系数；kag为骨料综合作用修正系数；ks为钢筋阻滞作用修正系数.

2.3 耐久性评价流程

对耐久性进行评价的流程见图15，首先，确定耐久性评价目的、范围和内容；然后，进行初步调查并对需要的参数进行详细检测，对检测数据进行概率统计；最后，对检测统计得到的数据进行数理分析，作出耐久性评价.

图15 耐久性评价流程图

3 实例分析

南浔区Y073老三济桥改造工程，原结构形式为六片铰接空心板，为了提高横向连接的可施工性与耐久性，将其改为横向五片刚接空心板.断面图见图16.

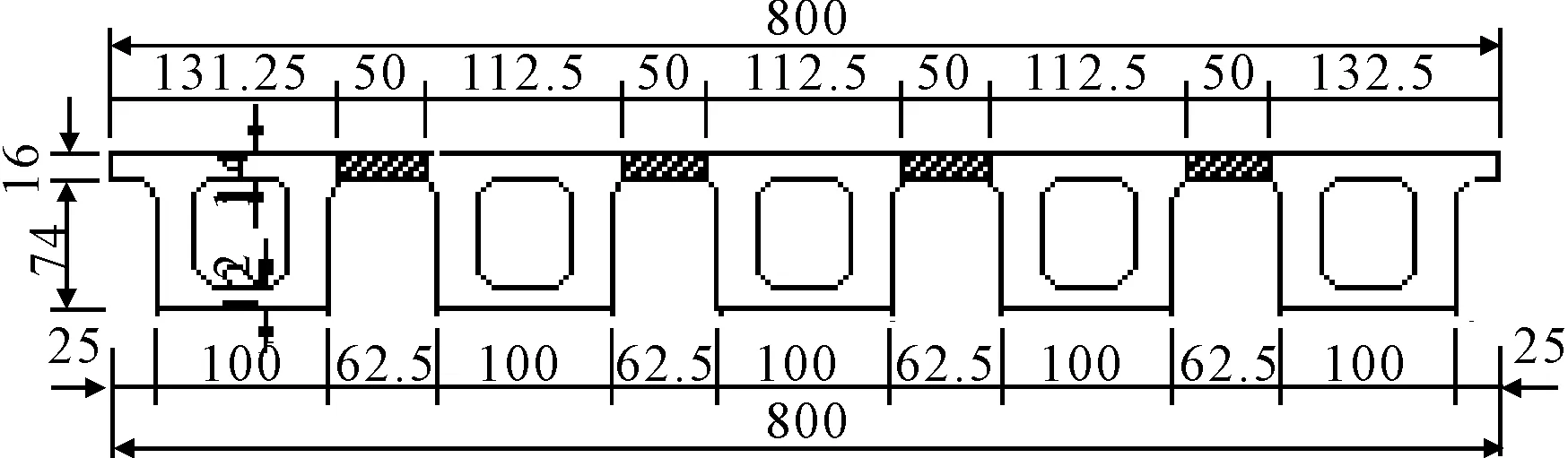
图16 全桥断面图(单位：cm)

对相关试验参数进行现场检测数据采集，选用线形结合机制对该桥进行耐久性寿命的概率分布特征进行分析，并在此基础上应用基于可靠度理论的耐久性寿命预测方法对该桥RC空心板进行耐久性寿命预测[11-15].检测所得各参数的概率分布特征统计见表4.

表4 各参数概率分布特征

在取得表4中的各项参数之后，将表4中的各项参数值代入修正后的线性结合机制下的寿命预测模型中进行蒙特卡罗模拟(选取的样本容量为2 000)，求得该桥RC空心板的耐久性寿命分布特征.通过计算，得到该桥RC空心板耐久性寿命频数直方图见图17，从直方图可以很清楚地看出，该桥RC空心板耐久性寿命呈偏态分布特征，其分布概率密度见图18.

图17 结构耐久性寿命频数直方图

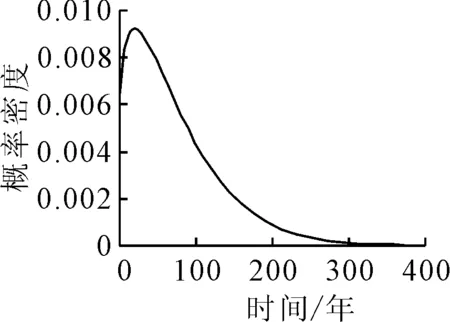
图18 结构耐久性寿命概率密度

图19为该桥梁服役50年时RC空心板的结构抗力(保护层厚度)与荷载效应(达到临界氯离子浓度值的深度)之间的概率分布关系.当可靠指标等于规定值时，根据可指标与时间关系曲线上便可得到RC空心板的耐久性寿命.根据文献[11]，结构耐久性极限状态所对应的设计使用年限的保证率应在90%～95%，那么对应的失效概率就在5%～10%，相应的可靠指标β的取值为1.282～1.645.本节对该桥RC空心板进行寿命预测时偏于安全的选取失效概率为5%，即可靠指标β为1.645，得到该桥RC空心板的耐久性寿命为46年.

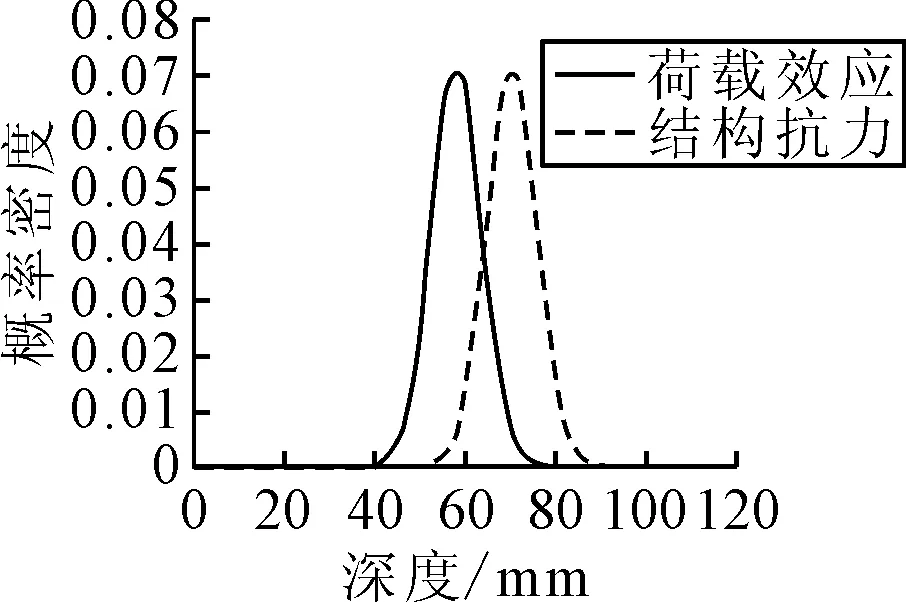
图19 服役50年时抗力与荷载效应概率分布

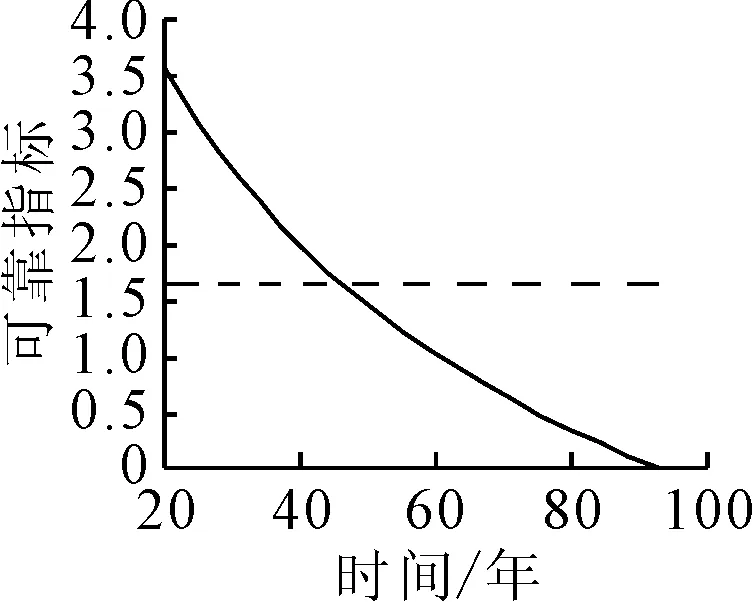
图20 可靠指标与时间的关系

4 结 束 语

文中考虑了混凝土本身的非匀质特性，采用数值模拟方法从细观尺度入手对氯离子在混凝土结构中的扩散规律进行研究.提出了细观模拟假设，并对细观尺度上的钢筋混凝土结构进行了简化：把混凝土视为由砂浆基质、界面过渡区和骨料混合而成的非匀质组合材料.根据实际情况，一改将混凝土视作匀质材料的思路，对骨料、砂浆基质及界面过渡区赋予不同的扩散特性，研究氯离子的扩散规律.在一定程度上考虑了骨料及钢筋不能作为氯离子扩散介质的特性，并提出了相关修正系数，为氯离子侵蚀环境中的钢筋混凝土结构耐久性评价以及耐久性设计提供了更为可靠的理论依据.并以某工程实例的RC空心板为算例，根据2节的分析结果对钢筋混凝土结构在氯离子侵蚀环境中的耐久性进行评价，得到该桥的耐久性寿命.