三维颅面水平参考平面的确定方法

金珉廷，刘 怡

(北京大学口腔医学院·口腔医院，正畸科 国家口腔疾病临床研究中心 口腔数字化医疗技术和材料国家工程试验室 口腔数字医学北京市重点实验室，北京 100081)

头影测量分析在口腔正畸临床中是不可或缺的一部分，也是临床医生做出正确合理的诊断和治疗设计的依据，其中头位是头影测量应用的基础[1]。由于获取影像过程中出现对象姿势的变化造成个体差异，测量之前头颅影像的再定位(reorientation)是必然的过程。确定头位可通过两种方法实现，即颅内和颅外。颅内确定头位方法指以颅内解剖标志点为基础构建平面而确定头部位置；颅外确定头位方法指是通过视线等，以反映个体实际形态或生理特性而确定个体头部位置[2]。在传统二维头颅侧位片上，将经过眶下点(orbitale，Or)和耳点(porion，Po)构成眶耳平面(frankfort plane，FH plane)，或蝶鞍点(sella, S)和鼻根点(nasion，N)连线构成前颅底平面(SN plane)作为经典的颅内构建水平面确定头位的方法。一直认为“自然头位(natural head position, NHP)”是最普遍而标准化的颅外头位确定方法，具有高度可重复性，定义为两眼平视前方，视线轴与地平面平行[3]，并且认为FH平面与地平面平行时头部位置几乎与自然头位一致[4]，但是在1956年Downs[5]通过100个青少年的侧面相与头颅侧位片结合证明，颅内FH平面与自然头位之间可产生向上或向下10°的偏差，在临床设计分析中一定要慎重考虑。之后，多数研究证明了FH平面和自然头位确定的头部位置不一致[6-7]。随着计算机技术发展，大视野锥形束CT(cone beam computed tomography，CBCT)影像超越了二维头影测量学的局限性，这种技术的应用使硬组织和软组织结合解释立体颅面部成为可能[8-11]。关于头位确定的研究也开始使用三维影像，使其更加完善。目前对于三维头颅影像的再定位，仍然基于耳点和眶下点构成的水平面。使用立体的三维影像无双侧结构、标志点重叠的问题，即构建水平面可选用双侧耳点和双侧眶下点[12-13]，但是由于人体普遍存在不对称性，双侧4个标志点同时在一个平面很难。目前有研究表明，在三维头颅影像中双侧耳点和双侧眶下点随机选取三个点构建4种水平面，并与传统二维影像构建的FH平面进行比较，结果显示差异无统计学意义[14]。应用颅面部三维影像可以足够清楚地观察到标志点的位置，但是由于存在双侧解剖结构的形态和/或位置上的不对称，在三维空间当中，双侧耳点和双侧眶下点同时构建一个水平面是很难的。本研究通过比较三维头颅影像中在双侧耳点和双侧眶下点中随机选取三个点构建的4种水平平面，并进一步检验头部位置的变化对于双侧耳点和双侧眶下点位置的影响，为三维头影测量确定水平参考平面提供理论依据。

1 资料与方法

1.1 资料

选择2016年4月至2017年7月于北京大学口腔医院正畸科就诊的患者32例，年龄13～51岁，平均(20.2±9.54)岁，其中男性7例，女性25例。纳入标准：(1)恒牙列；(2)颏下点(menton，Me)离正中矢状面的距离≤2 mm[15]，面部基本协调对称，无明显畸形；(3)无正畸治疗或正颌外科手术史；(4)无肿瘤、唇腭裂等颅面部疾病；(5)无面部外伤史；(6)全身状况良好，无全身疾病史。排除标准：(1)乳牙列；(2)多生牙，牙列缺损；(3)Me点离正中矢状面的距离>2 mm；(4)面部先天性畸形或外伤史；(5)正畸或正颌外科手术史。本研究经过北京大学口腔医院伦理委员会审查批准(PKUSSIRB-201631133)， 所有参与研究的对象均签署知情同意书。

1.2 数据获取

用CBCT扫描仪(NewTom VG Volumetric Scanner，Aperio公司，意大利)获取正畸患者的数据,扫描范围从颅骨顶部至颏部。扫描参数：电压110 kV，电流1～20 mA，投照范围为15 cm×15 cm，空间分辨率为0.30 mm，放射时间约3.6 s。扫描数据以DICOM格式储存。

1.3 测量

进行4种不同水平参考平面在三维虚拟空间中旋转角度的测量，首先在Dolphin软件中导入DICOM格式的CBCT数据，本研究采用的解剖标志点见表1。为了减少定点误差，三维头颅影像渲染图与多维图结合进行双侧耳点和双侧眶下点的定点，并保存(图1)。进入软件3D 定向页面，借助红色参考线，将水平面调整至其所定义的位置。为了构建一致的坐标系，正中矢状面在三维渲染图与多维图结合应用下，使参考红线经过N点、S点和枢椎齿突最高点(Dent)的位置而构建。从双侧耳点和双侧眶下点(共4个标志点)中随机选取三个点构建4种不同水平面，分别定义为，平面1：水平面由双侧眶下点与右侧耳点构成，简称Rp平面；平面2：水平面由双侧眶下点与左侧耳点构成，简称Lp平面;平面3：水平面由双侧耳点与右侧眶下点构成，简称Ro平面；平面4：水平面由双侧耳点与左侧眶点构成，简称Lo平面(图2)。在软件三维虚拟空间当中计算的旋转角度为俯仰角(Pitch)、 侧偏角(Yaw) 和横滚角(Roll)， 其定义见表2、3和图3。根据Oh等[14]建议以双侧眶下点和右侧耳点构建的水平面作为参照，即本研究以Rp平面为基准，记录以软件全局坐标系计算的每一平面与之旋转角度的差异(表4)。将研究对象根据年龄分为两组：(1)13～17岁组：男性5例、女性13例，共18例；(2)18岁以上组：男性2例、女性12例，共14例。不同年龄组分别以Dent点作为三维影像坐标系的原点测量双侧耳点和双侧眶下点位置，分析头部的转动对双侧耳点和双侧眶下点位置的影响。间隔两周由同一位研究者进行第二次水平面的确定，并记录测量值。

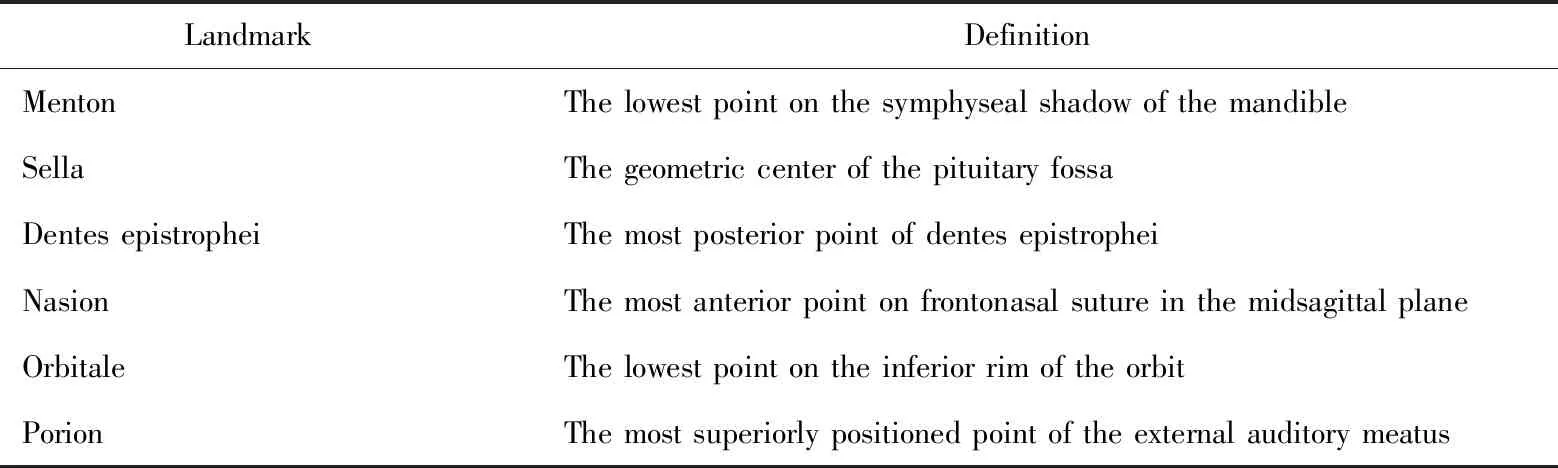
表1 解剖标志点的定义Table 1 Define of hard and soft tissue landmarks for head orientation

表2 旋转角正负的确定Table 2 Define of plus and minus to confirmed direction of 3D rotation

表3 三维旋转角度的定义Table 3 Define of 3D rotation degrees

MSP, mid-sagittal plane.

1.4 统计学分析

应用SPSS Statistics(Version 20，IBM，Chicago, US)软件，计算组内相关系数(intraclass correlation coefficient，ICC)， 比较两次测量结果的一致性，检验测量者自身的可靠性。进行单因素重复测量方差分析检验组内4个平面之间的差异。双侧检验水准α=0.05，P<0.05为差异具有统计学意义。

2 结果

2.1 计算ICC

两周后重复测量数据与第一次测量数据计算ICC分别为：Rp平面的r=0.987，Lp平面的r=0.892，Ro平面的r=0.891，Lo平面的r=0.832。两次测量结果自身的可靠性高，其中双侧眶下点与右侧耳点构建的Rp平面一致性最高。

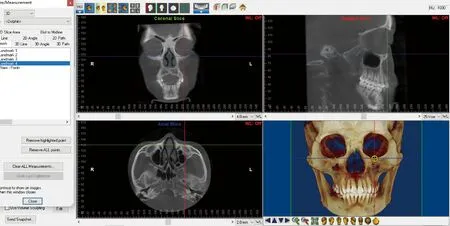
图1 双侧眶下点和双侧耳点的定点Figure 1 Tracing the bilateral orbitale and bilateral porion

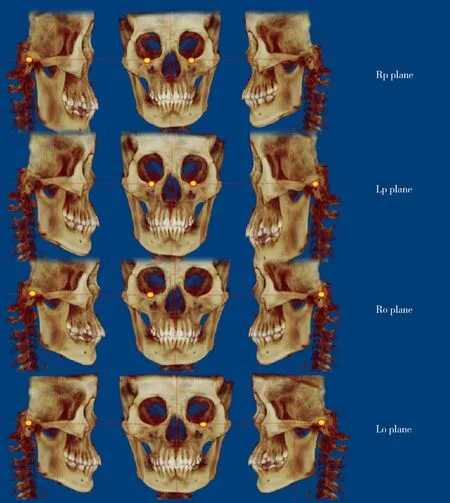
图2 4种水平平面的确定: Rp平面由双侧眶下点与右侧耳点构成；Lp平面由双侧眶下点与左侧耳点构成；Ro平面由双侧耳点与右侧眶下点构成；Lo平面由双侧耳点与左侧眶点构成Figure 2 Define of horizontal planes：Rp plane constructed by bilateral orbitale and right porion; Lp plane constructed by bilateral orbitale and left porion; Ro plane constructed by bilateral porion and right orbitale; Lo plane constructed by bilateral porion and left orbitale

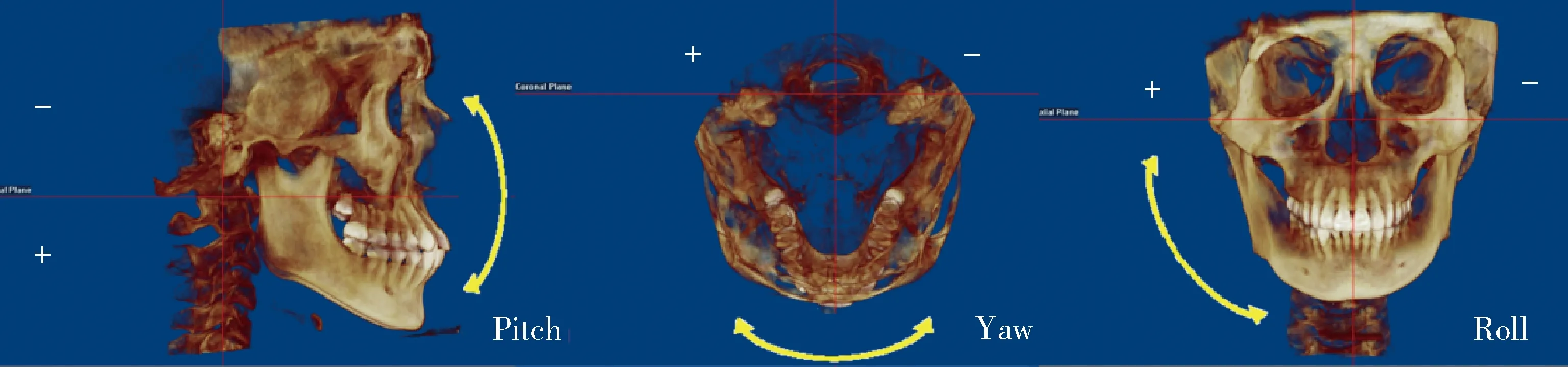
图3 三维虚拟空间旋转角度的定义Figure 3 Define of 3-dimensional rotation degree

2.2 4种水平面的比较

以Rp平面为基准(设置Rp平面Pitch=0、Yaw=0、Roll=0)平面，Lp、Ro、Lo旋转程度的均数±标准差见表4。正负代表方向，可见组内不同平面旋转角度≤0.2°。单因素重复测量方差分析比较组内4种不同水平面之间三维旋转角度的差异，结果组内4种水平参考平面的俯仰角P=0.196、侧偏角P=0.314、横滚角P=0.341, 均无统计学意义(P>0.05)。

2.3 头位转动与标志点位置关系

根据年龄将研究对象分为两组进行计算：(1)13～17岁组：男性5例、女性13例，共18例；(2)18岁以上组：男性2例、女性12例，共14例。以Rp平面为参照，Dent点作为原点(origin point)分别计算双侧耳点和双侧眶下点位置的均值和标准差(表5)。应用圆周长公式(圆周长= 2πr)计算头部产生1°转动对不同标志点产生的位置变化(表6)。

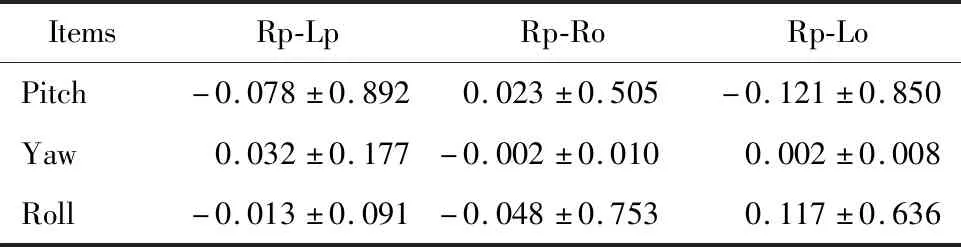
表4 以Rp平面为基准不同平面之间旋转角度的差异/(°)Table 4 Rotation degree differences between three planes with Rp plane respectively/(°)

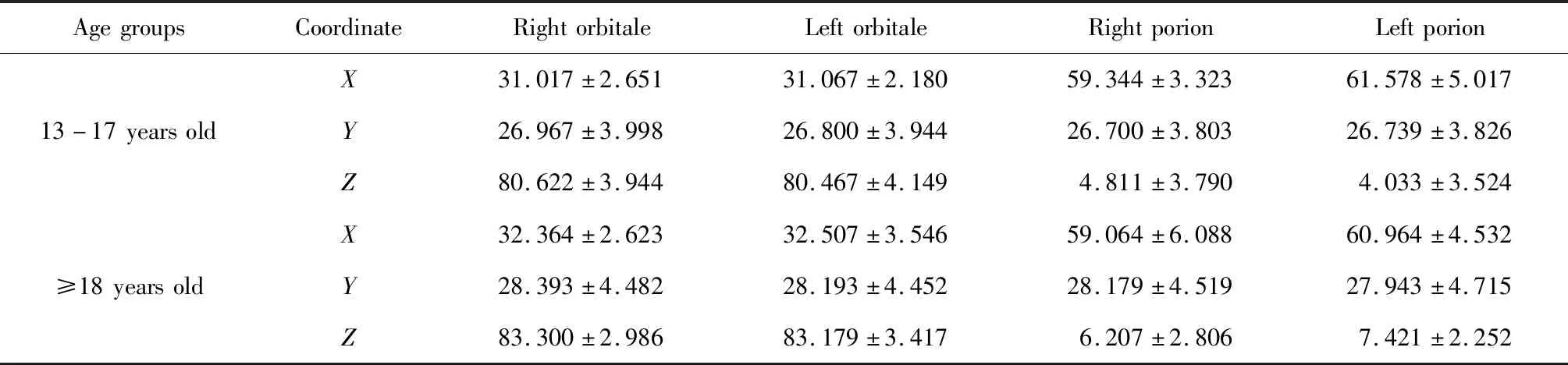
表5 不同年龄段以Dent点为原点的标志点的位置/mmTable 5 Landmark coordinates in different age groups/mm

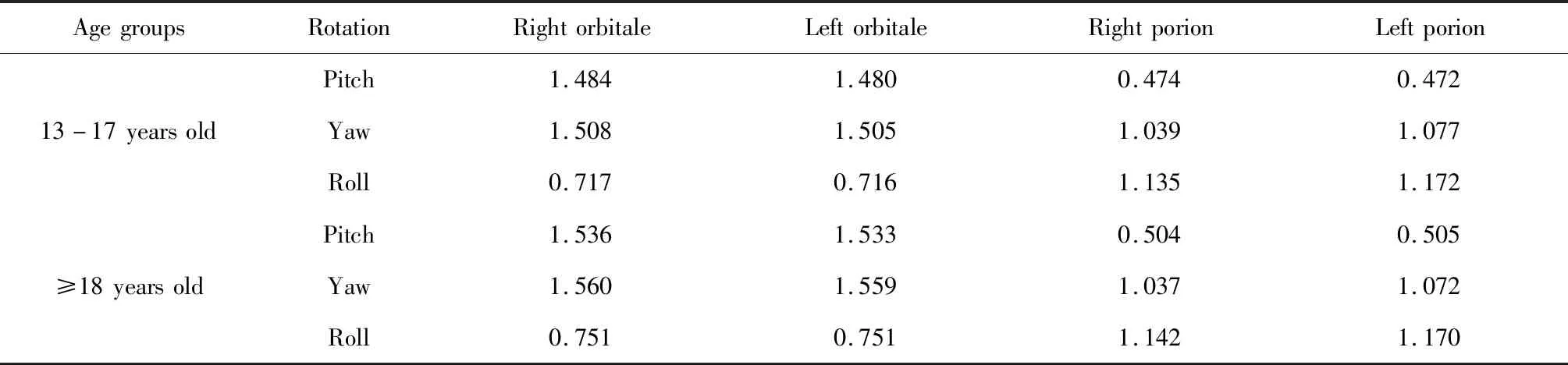
表6 不同年龄段以Dent点为原点计算头部不同方向1°转动对双侧耳点和双侧眶下点产生的距离变化/mmTable 6 Based on different ages apply the circumference formula calculated change of bilateral porion and orbitale position generated by head rotation in different directions/mm

3 讨论

3.1 传统水平面的确定

3.2 三维正中矢状面的确定

应用三维头颅影像构建正中矢状面(mid-sagittal plane， MSP)的方法大致有三种，不同正中矢状面的位置会增加面部的不对称性，也会造成三维头影测量值的误差[19]。构建正中矢状面的方法有：(1)利用解剖标志点的点构法；(2)普氏分析法；(3)迭代最近点算法。点构法常用的解剖标志点有N点、S点、前鼻棘点(anterior nasal spine，ANS)、颅底点(basion，Ba)和Dent点[12, 20]。迭代最近点算法和普氏分析法是通过应用逆向工程软件使用独特计算公式求得正中矢状面的方法。Xiong等[21]研究迭代最近点算法和普氏分析法之间差异无统计学意义，两种方法均适合用来确定正中矢状面。王斯维等[22]比较构建正中矢状面的三种方法，结果迭代最近点算法和点构法之间差异无统计学意义，但是这两种方法与普氏分析法之间差异有统计学意义。目前迭代最近点算法和点构法被认为比较可靠，因此，本研究为了排除不同软件之间数据转换产生的误差和为了实验简化，使用了N点、S点和Dent点来构建正中矢状面。

3.3 三维水平面的确定

三维影像的出现和发展使立体的牙颌颅面部软硬组织解剖结构清晰、准确定点成为可能。应用三维头颅影像再定位的核心步骤是坐标系的建立和设置原点。三维头颅影像的坐标系由水平面、正中矢状面、冠状面构成。目前三维颅面影像构建水平面的方法主要有：(1)选用双侧耳点与一侧眶下点构建；(2)选用双侧眶下点与一侧耳点构建；(3)选用双侧耳点与双侧眶下点连线中点构建；(4)选用双侧眶下点与双侧耳点连线中点构建。Oh等[14]比较传统二维头颅侧位片与三维头颅影像相应的测量值，结果显示传统二维头颅侧位片构建的FH平面与在三维影像中由双侧耳点和双侧眶下点随机选取三个点构建的4种水平面之间差异无统计学意义，相关系数约为0.7。Lim等[23]比较以上四种方法构建的水平面和外侧半规管平面(lateral semicircular canal plane，LSP)， 以面部对称10例、面部不对称10例、唇腭裂10例为研究对象，结果显示5种三维颅面水平参考平面的测量者自身可靠性(组内)及3个不同测量者之间(组间)差异无统计学意义。本研究为了减少定点误差，应用Dolphin软件中定位功能，结合使用红色参考线和多维图来准确地确定双侧耳点和双侧眶下点位置而构建不同水平面。

3.4 解剖标志点的位置

临床头影测量分析结果使用毫米(mm)或者角度(°)来表示，常用标志点位置的变化是需要关注的内容，因此，本次研究进一步分析了头部三维方向的转动对双侧耳点和双侧眶下点位置的影响。目前Kim等[24]应用CBCT研究软组织和硬组织双侧耳点在三维空间中的位置关系，将双侧软组织和硬组织耳点连线，以一侧耳点设置为原点，分别计算发生1°旋转时对侧耳点产生的距离变化，结果显示硬组织耳点发生约2.0 mm的变化，软组织耳点发生约2.5 mm的变化，但是人的头部以枕环关节为轴发生各方向的转动，因此，本研究以Dent点为原点计算头部不同方向1°转动对双侧耳点和双侧眶下点产生的距离变化。由于颅面部形态及各标志点位置的测量受到生长发育的影响，本研究将研究对象分为两组进行分析，分别为13～17岁组和18岁以上组，结果显示不同方向的头部转动对双侧耳点和双侧眶下点产生不同的距离变化，无论在什么年龄段，双侧眶下点发生1°俯仰角和侧偏角变化时产生1 mm以上距离变化；双侧耳点发生1°侧偏角和横滚角变化时产生1 mm以上距离变化。

本研究在三维头颅影像中选取双侧耳点和双侧眶下点构建4种不同水平面，并测量俯仰角、侧偏角、横滚角。通过本次研究和以往研究结果，临床建议使用双侧眶下点和右侧耳点构建的三维影像水平面，即本研究中的Rp平面确定头位。本研究选取面部基本对称的病例，虽然测得的水平面之间旋转角度差异无统计学意义，但不为零，说明个别对象的双侧耳点和双侧眶下点位置不完全一致，即若选取双侧眶下点后可能双侧耳点位置不一致，反之亦然。本研究不足以解释面部不对称性与选取双侧耳点和双侧眶下点构建三维水平面是否有关，是否与上下颌矢状骨性畸形有关，因此，需要进一步确定最稳定可靠的三维水平面构建方法。