前景理论视角下专利代理服务模式优化研究

陈 伟， 林超然， 李金秋， 杨早立， 林 艳

(1.哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001; 2.北京工业大学 经济管理学院，北京 100124; 3.东北农业大学 经济管理学院，黑龙江 哈尔滨 150030)

0 引言

中国是专利申请大国，专利申请量连续6年位居世界首位[1]，但从专利的平均维持年限、说明书页数和权利要求项数等指标来看，我国与发达国家相比在专利质量上仍存在较大差距[2,3]。专利代理服务是连接技术发明人与知识产权行政管理部门的重要媒介，专利代理机构通过专业化运作，将技术发明人的智力成果转化为受法律保护的知识产权，能够提高专利申请效率、保护科技创新成果、扩大专利权利要求[4,5]，有助于促进专利质量提高。但专利代理服务本质上是一种“委托―代理”关系，存在目标不一致、信息不对称现象[6]，其表现在：专利代理机构追求专利申请成功，而技术发明人也同时注重专利质量；专利代理机构了解技术的法定性，而技术发明人则更清楚专利的技术性和商业性。这种“委托―代理”关系影响了专利代理合作效率的提高[7,8]。

针对一般意义上的“委托―代理”问题，2016年诺贝尔经济学奖获得者Hart和Holmstrom[9]提出了道德风险下“委托―代理”关系的一般模型，并给出了不完全信息下解决此类问题的条件。在此分析框架内，学者通过引入利润分配来防范技术创新过程中道德风险，如：黄波等[10]设计出一种产出分享加固定转移支付的混合分配方式，可规避研发外包中的双边道德风险；Kong等[11]指出建立收益共享契约可促进供应链信息的共享，缓解信息不对称现象；杜欣[12]指出必须调整合作双方的创新利润分配模式，才能使双方共同享有协同创新收益，调动创新积极性；时茜茜等[13]发现分享收益可激发承包商与供应商的协同合作积极性；贺一堂等[14]指出产出分享方式能够激励产学研合作。通过上述研究可以发现，将利润分配机制引入专利代理活动中，引导专利代理活动参与者采取共赢的行为策略，是提升专利代理服务效果、提高合作效率的重要方向。目前，在专利代理活动中，“委托―代理”问题的解决大多从提高专利代理机构专业性、增加共有知识、弥补双方信息不对称等角度进行，如：Li Changli等[15]使用PAFM模型分析，指出代理人的专业知识是激励技术发明人参与代理活动的重要因素；Gu Li等[16]指出提高专利代理机构的专业性可缓解对接障碍；潘瑾和陈媛[17]提出构建可量化的服务质量指标体系以规范代理机构行为；此外，一些学者能够通过建立博弈模型的方式处理专利活动中收益分配问题，如：刘利和朱雪忠[18]指出利润分配上竞合双方需考虑未来整体利润预期，才有可能实现博弈均衡。

经梳理后发现，现有研究仍存在以下不足之处：相关研究尝试通过减少双方信息差异来解决“委托―代理”问题，但专利技术领域众多，专利代理机构很难缩小知识储备差距；相关研究基于完全理性的期望效用理论，未能考虑博弈参与者在决策过程中的心理因素对决策的影响，而决策者普遍存在损失厌恶心理、参照点效应等有限理性倾向[19,20]，这种倾向对创新努力程度[21]以及收益共享契约的协调[22]均存在影响；相关研究均采用宏观、静态视角，而实际上，由于缺少全局信息，专利代理服务活动中，参与者的策略选择并非一成不变，而是随着环境不断变化的，决策个体在识别判断、准确行为等方面存在能力差异，需要在反复博弈中互相模仿并渐进学习，因而是一种微观的动态演化过程。

因此，为解决上述问题，本文将专利代理服务策略选择视为渐进学习过程，从微观层面构建专利代理预期收益分配策略，利用前景理论的价值函数和权重函数刻画有限理性的行为人在缺乏全局信息下的感知和决策行为，构建博弈参与者的收益感知矩阵；利用演化博弈模型建立有限次重复博弈过程，探讨专利代理服务双方博弈过程中策略的形成及演化，通过分析演化博弈动态系统均衡点，探讨代理服务双方策略演化的稳定选择，利用Matlab数值仿真揭示影响稳定策略的关键变量，进而为建立更完善的专利代理服务模式提供理论指导。

1 基本假设与模型构建

Kahneman和Tversky在大量实验的基础上指出，人对损失的反应比等量收益强烈。因此，前景理论中价值函数是收益的凹函数、损失的凸函数，且后者曲率比前者更陡峭(图1)[23]。受其影响，技术发明人与专利代理机构在服务撮合过程中，技术发明人对支付代理费用的心理价值判断会显著高于期望值，而专利代理机构对获得代理收入的心理价值判断会显著低于期望值。此外，专利获得授权的不确定性会产生不同的权重感知反馈，Kahneman等人发现，在面对不确定因素时，决策者会低估大概率事件而高估小概率事件，需采用权重函数(图2)做调整。两种效应导致现实中博弈双方在进行交易撮合时无法准确预判彼此策略反馈，影响了专利代理服务的规模和效果。因此，考虑到心理因素对专利代理服务双方策略选择的影响，本文使用前景理论刻画双方的认知和决策过程。

图1 前景理论的价值函数

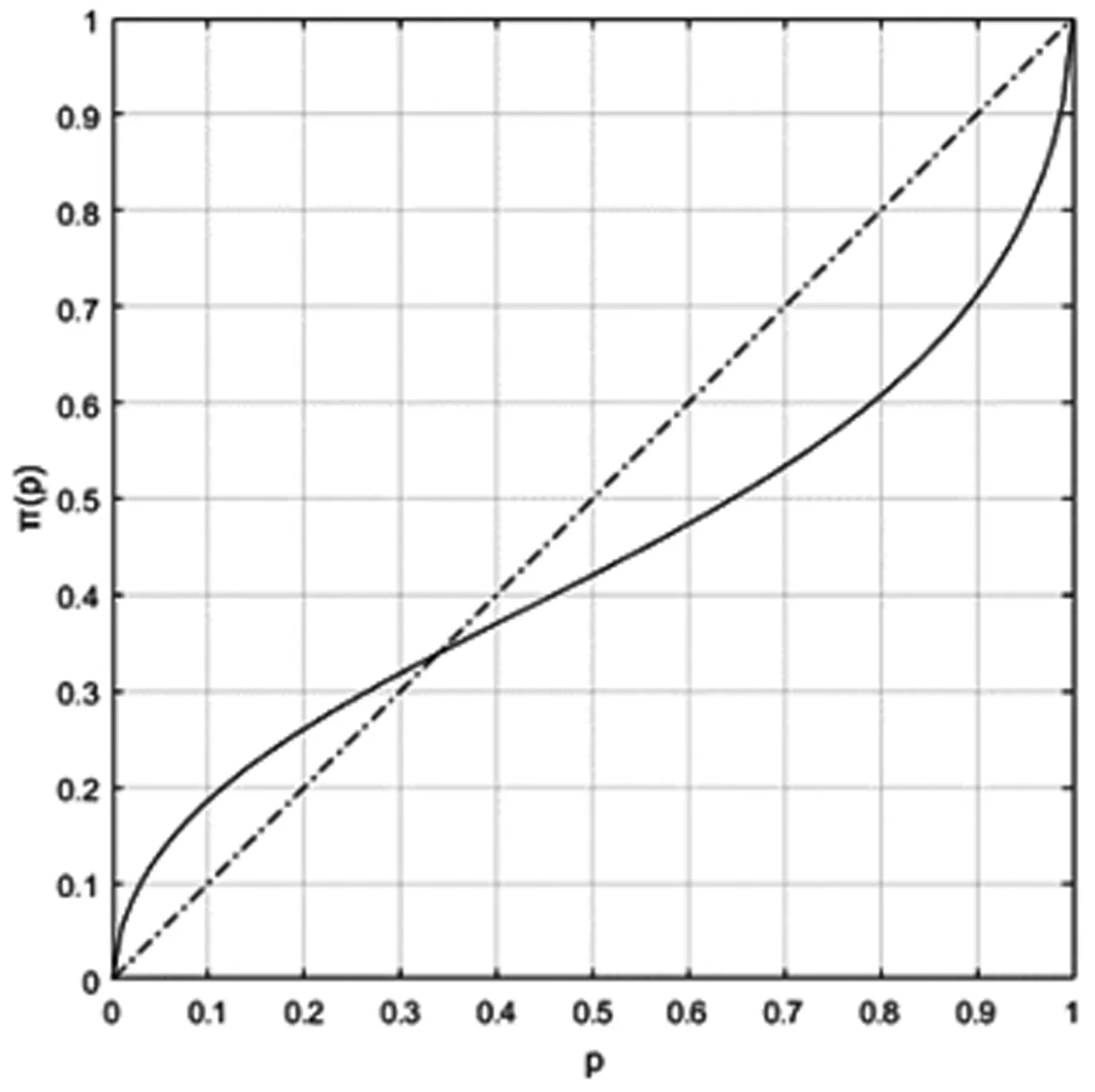
图2 前景理论的权重函数

价值函数和权重函数可由式(1)～(3)表示：

Δr=r-r0

(1)

(2)

(3)

其中Δr为价值变动，r为实际价值，r0为参照价值点(Reference Price)，v(Δr)为对价值变动的感知，η为价值边际敏感程度(0<η<1)，λ为损失规避系数(λ>0)，p为客观概率，π(p)为主观概率，γ为权重函数曲线的曲率。

前景价值可表示为式(4)，即各项收益变动事件的价值函数和权重函数乘积之和：

(4)

基于前景理论的有限理性假设，本文构建一种专利预期收益分配契约，进而激励专利代理服务参与者，引导双方采取共赢的行为策略。为了方便后文讨论，根据专利代理机构及技术发明人之间的交易特点，构建专利预期收益分配假设如下：

假设1存在专利代理机构和技术发明人两个博弈参与群体。专利代理机构的行为集为：“预期收益分配模式”和“传统模式”；技术发明人的行为集为：“违约”和“履约”。其中，专利代理机构选择预期收益分配模式、技术发明人选择履约是博弈的最优状态，在这一状态中，博弈双方能够顺利合作，共同探索专利的长期价值，专利代理服务效果得到保证。

假设2专利代理机构采用预期收益分配模式的比例为x(0≤x≤1)，采用传统模式的比例为1-x，技术发明人履约比例为y(0≤y≤1)，违约比例为1-y。

假设3①技术发明人可感知三种类型费用：向代理机构支付的代理费、专利预期收益分成以及违约罚金；可感知两种收益：专利预期收益和违约获益。②专利代理机构可感知两种类型费用：固定服务成本(包括人员劳务成本、申请费、实质审查费以及可能产生的复审费)和技术发明人违约造成的损失；可感知三种类型的收益：代理费、专利预期收益分成以及技术发明人违约罚金收益。

假设4专利代理服务过程中只考虑技术发明人以及专利代理机构两个主体，博弈过程中双方仅具有有限理性，双方依据自身对收益和风险的心理感知进行决策，收益感知服从价值函数、决策权重服从权重函数。

假设5专利获得授权概率(k)与技术本身特征、专利代理机构能力有关，与双方的策略选择无关。

综上，符号设定如表1所示：

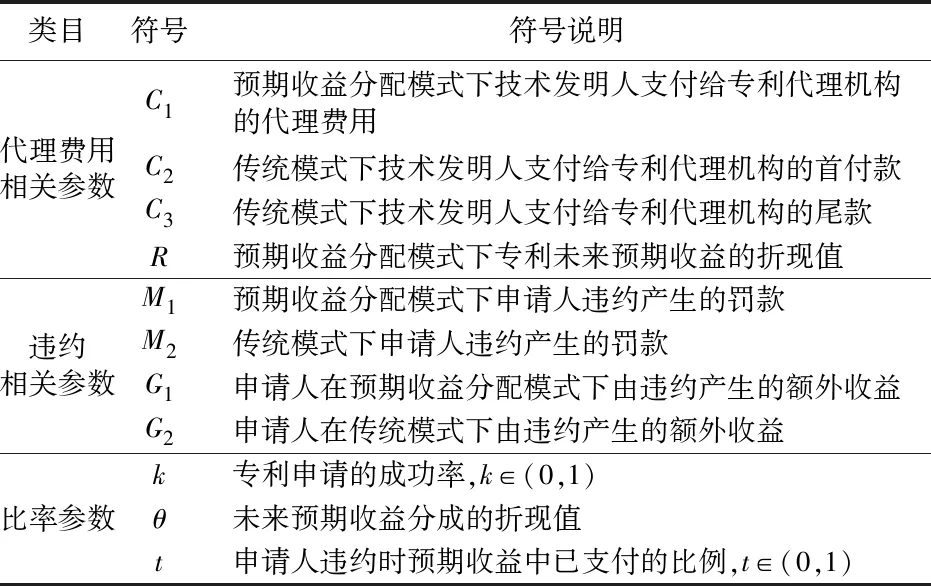
表1 符号说明

根据上述假设，构建不完全信息下有限理性的专利代理服务参与者的博弈模型，博弈双方的收益感知矩阵如表2所示：

表2 博弈双方收益感知矩阵

专利代理机构的收益用An表示，技术发明人收益使用Bn表示，双方采用不同策略时面对不同的收益感知：

(1)当专利代理机构选择预期收益分配模式，技术发明人选择履约时：

技术发明人向专利代理机构支付代理费C1，专利获得授权可能性为k，获得授权后，持续获利折现后为R，技术发明人将这部分获利以分成的方式支付给专利代理机构，支付比例为θ。因此根据前景理论：

①专利代理机构对收益的感知为：A1=π(k*)×v(C1)+π(k*)×V(R×θ)。由于专利代理机构一定可获得代理费，因此π(k*)≡1，上式可简化为：A1=v(C1)+π(k)×v(R×θ)，下同。

②技术发明人对收益的感知为：B1=v(-C1)+π(k)×v(-R×θ)+π(k)×v(R)。

(2)当专利代理机构选择预期收益分配模式，技术发明人选择违约时：

技术发明人向专利代理机构支付代理费C1，专利获得授权可能性为k，专利获得授权后，持续获利折现后为R，技术发明人将这部分获利以分成的方式支付给专利代理机构，支付比例为θ。产生违约时，预期收益已支付的比例为t，技术发明人因违约产生收益为G1，按照合同需赔偿专利代理机构M1。因此：

①专利代理机构对收益的感知为：A2=v(C1)+π(k)×v(R×θ×t)+v(M1)

②技术发明人对收益的感知为：B2=v(-C1)+π(k)×v(-R×θ×t)+v(-M1)+π(k)×v(R)+v(G1)

(3)当专利代理机构选择传统模式，技术发明人选择履约时：

技术发明人向专利代理机构支付代理费首付款C2，专利获得授权则支付尾款C3，获得授权概率为k。因此：

①专利代理机构对收益的感知为：A3=v(C2)+π(k)×v(C3)

②技术发明人对收益的感知为：B3=v(-C2)+π(k)×v(-C3)+π(k)×v(R)

(4)当专利代理机构选择传统模式，技术发明人选择违约时：

技术发明人支付首款C2，并获得预期收益折现值R，因违约向专利代理机构支付违约金M2，因违约获得收益G2。

①专利代理机构对收益的感知为：A4=v(C2)+v(M2)

②技术发明人对收益的感知为：B4=v(-C2)+v(-M2)+π(k)×v(R)++v(G2)

上述技术发明人及专利代理机构的收益感知情况如表3和表4所示。

表3 专利代理机构收益感知表

表4 技术发明人收益感知表

2 策略选择的演化博弈分析

2.1 演化动态系统的均衡点

状态S={(S11,S12),(S21,S22)}={(x,1-x),(y,1-y)}可用[0,1]×[0,1]上的点(x,y)表示，用以描述专利代理过程中，专利代理机构和技术发明人不同策略组合的演化动态。根据Malthusian动态方程计算相应的收益感知：

专利代理机构选择预期收益分配模式时的收益感知为：

E(S11)=y×A1+(1-y)A2

(5)

专利代理机构选择传统模式时的收益感知为：

E(S12)=y×A3+(1-y)A4

(6)

专利代理机构平均的收益感知为：

E(S1)=x×E1(S12)+(1-x)×E(S12)

(7)

技术发明人选择履约时的收益感知为：

E(S21)=x×B1+(1-x)B2

(8)

技术发明人选择违约时的收益感知为：

E(S22)=x×B3+(1-x)B4

(9)

技术发明人平均的收益感知为：

E(S2)=y×E(S21)+(1-y)×E(S22)

(10)

根据泰勒-齐克提出的动态调整选择机，双方策略的调整速度为：

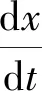
(11)

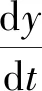
(12)

因此，联立微分方程可得该动态系统的均衡点为：E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)以及E5(x*,y*)。

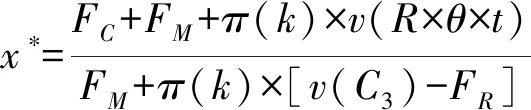
(13)

(14)

为便于表述，式(13) (14)中：FC=v(C1)-v(C2)，代表C1与C2造成的心理感知差异；同理F-C=v(-C1)-v(-C2)，FM=v(M1)-v(M2)，F-M=v(-M1)-v(-M2)，FG=v(G1)-v(G2)，FR=v(R×θ)-v(R×θ×t)，F-R=v(-R×θ)-v(-R×θ×t)。

2.2 均衡点的稳定性分析

利用雅克比矩阵的局部稳定性来判断五个稳定点的邻域函数特征，雅可比矩阵为：

(15)

雅克比矩阵的行列式与迹为：

detJ=J11×J22-J21×J12

(16)

trJ=J11+J22

(17)

计算得到：

J11=(2x-1)×[(y-1)×(FG+F-M)-

F-C-π(k)×v(-R×θ×t)+

y×π(k)×(v(-C3)-F-R)]

(18)

J12=x×(x-1)×[FG-F-M+π(k)×(v(-C3)-F-R)]

(19)

J21=y×(y-1)×[FM+π(k)×(v(C3)-FR)]

(20)

J22=(1-2y)×[FC+(1+x)×FM+π(k)×

(v(R×θ×t))+x×π(k)×(v(C3)-FR)]

(21)

可得点(0,1)、(1,0)、(0,1)和(1,1)的行列式值与迹，如表5所示。由于点(x*,y*)处迹值为0，非均衡点，故表5中将其略去。

表5 各均衡点处的迹与行列式

化简可知，判定上述稳定点迹和行列式值需判定以下边界条件符号：

ψ1=-FC+π(k)×[v(C3)-v(R×θ)]

(22)

ψ2=-F-C+π(k)×[v(-C3)-v(-R×θ)]

(23)

ψ3=-F-C+π(k)×v(-R×θ×t)

(24)

ψ4=FC+π(k)×v(R×θ×t)

(25)

当ψ1、ψ2、ψ3和ψ4四个边界条件中任意一个为零时，动态系统无均衡点。现讨论四者均不为零的情况：

(1)当ψ1>0、ψ2≠0、ψ3>0且ψ4≠0时：

该条件下，动态系统均衡点的稳定性分析如表6所示，E2(1,0)是唯一稳定策略，系统的相位轨迹图(图3)描述了这一动态演化过程。此时，专利代理机构选择预期收益分配模式，技术发明人选择违约。

表6 局部稳定性分析

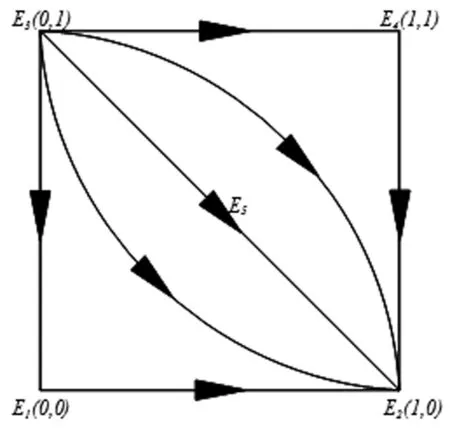
图3 策略动态演变

(2)当ψ1<0、ψ2<0、ψ3≠0且ψ4≠0时：

该条件下，动态系统均衡点的稳定性分析如表7所示，E4(1,1)是唯一稳定策略，系统的相位轨迹图(图4)描述了这一动态演化过程。此时，专利代理机构选择预期收益分配模式，技术发明人选择履约，E4(1,1)是专利代理服务的最优状态，代理服务参与者在这种合作策略下达成共赢，合作效率最高。这一稳定策略的存在表明，预期收益分配方案具有理论上的可行性。

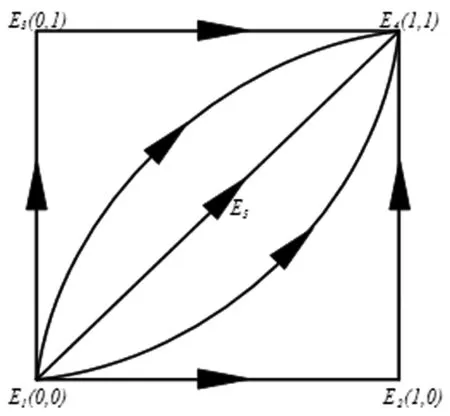
图4 策略动态演变

(3)当ψ1<0、ψ2>0、ψ3>0且ψ4>0时：

该条件下，动态系统均衡点的稳定性分析如表8所示，E3(0,1)是唯一稳定策略，系统的相位轨迹图(图5)描述了这一动态演化过程。此时，专利代理机构选择传统模式，技术发明人选择履约。

表7 局部稳定性分析

表8 局部稳定性分析

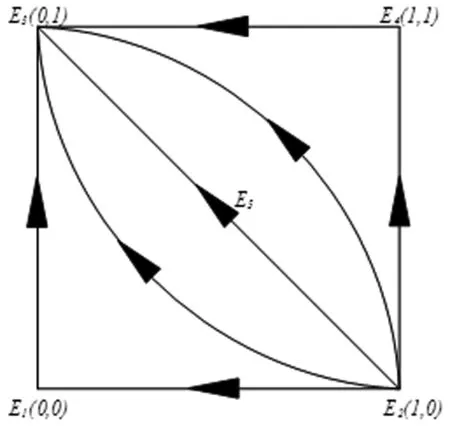
图5 策略动态演变

除以上三种情况外，动态系统不存在均衡点。综上可知，边界条件与均衡点的关系可整理如表9所示：

表9 边界条件与均衡点关系

2.3 模型结论

(1)不同初始条件通过前景理论价值函数和概率函数影响边界条件符号，进而影响博弈稳定策略。分析边界条件可知，对事件收益的心理感知水平，尤其是对不同策略的收益感知差异是影响稳定策略的关键。

(2)从博弈稳定策略的分布来看，无论初始条件如何改变，E1(0,0)和E5(x*,y*)始终不是演化稳定策略。表明：①混合策略始终不是稳定策略，博弈稳定时双方都会使用纯策略，并在特定纯策略处达到ESS；②专利代理机构服务无法形成“传统模式+违约”模式，表明传统代理服务模式对于防范违约是有效的。

3 数值仿真

为了探究专利代理服务过程中参数变化对系统演化的影响，本文对上述模型进行数值仿真，模拟专利代理过程中专利代理机构与技术发明人策略的动态演化过程。现假设有一项技术寻求专利代理服务，其技术长期预期收益的折现值为10万元，根据Kahneman和Tversky等[23]的研究，将前景理论的价值函数中的价值边际敏感程度η取值为0.88，损失规避系数λ取值为2.25，参照同类文献[24]将r取值为0.61。设系统演化的初始点为(0.5,0.5)，为避免单个特解对全局情况概括不全，本文使用Matlab软件生成初始条件在值域内的取值组合，剔除其中不符合上文假设的取值，并使用Runge-Kutt方法获得演化博弈解，绘制演化相位图谱，确定各初值的演化稳定点，并分析影响每个稳定点稳定性的关键变量。

(1)E(0,1)点稳定性的影响因素仿真分析

当C1=4000，C2=5000，C3=6000，t=0.3，θ=0.08，p=0.1时，满足边界条件ψ1<0、ψ2>0、ψ3>0且ψ4>0，此时演化博弈系统稳定点为E(0,1)，博弈双方的稳定策略为“传统模式”和“履约”。如图6所示，θ值变化会对博弈产生较大影响：当θ值不断变大，超过临界值0.0695时，稳定策略由E(0,1)向E(1,1)演变，即博弈稳定策略在技术发明人“履约”策略不变的前提下，专利代理机构的策略从传统模式向预期收益分配模式演变。

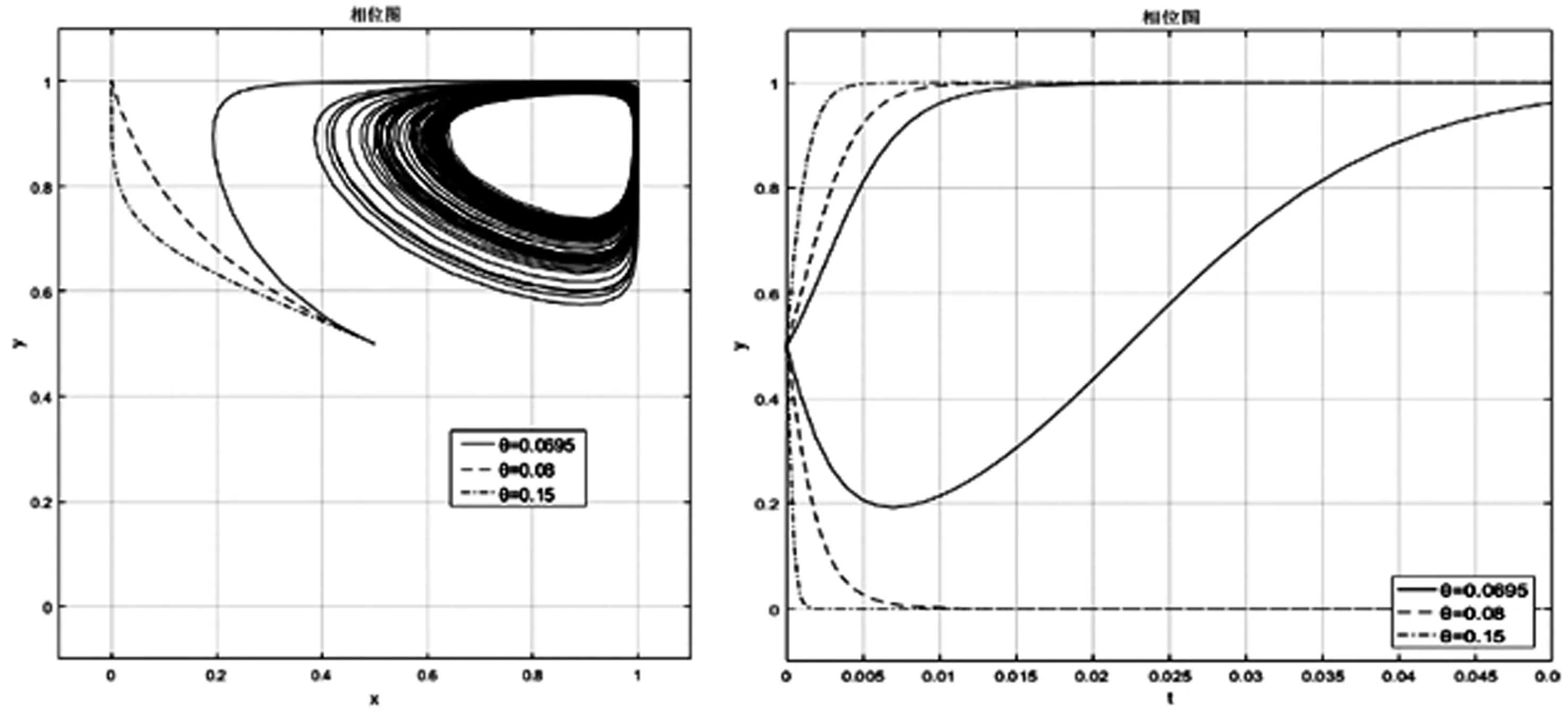
图6 θ值对稳定策略E(0,1)的影响

当预期收益分配模式中首付款C1逐渐增大时，均衡被打破，随着C1继续增大，均衡在新稳定策略点E(1,0)处重建，如图7所示。此时双方的选择为“预期收益分配模式”和“违约”。表明为避免技术发明人违约，提高专利代理费用会破坏合作关系。

由图6和图7可知，相较提高两种模式的首付款差别，从传统模式向预期收益分配模式演化的关键措施为提升预期收益分成比重。

(2)E(1,0)点稳定性的影响因素仿真分析

当C1=4000，C2=7000，C3=6000，θ=0.1，t=0.3，p=0.1时，满足边界条件ψ1>0、ψ2≠0、ψ3>0且ψ4≠0，此时演化博弈系统稳定点为E(1,0)，博弈双方的稳定策略为“预期收益分配模式”和“违约”。

为应对违约，专利代理机构如果选择提高预期收益分配模式下预期收益分成比重θ，会显著影响系统的稳定策略，当θ从0.1增大到0.14过程中，系统经历由稳定策略E(1,0)经由不稳定状态向稳定策略E(0,1)的转化，如图8所示。即：当系统位于预期收益分配模式服务下，且出现违约现象时，适当提高预期收益分配模式的分成比例能够避免技术发明人违约，但也会同时驱使双方选择传统模式。

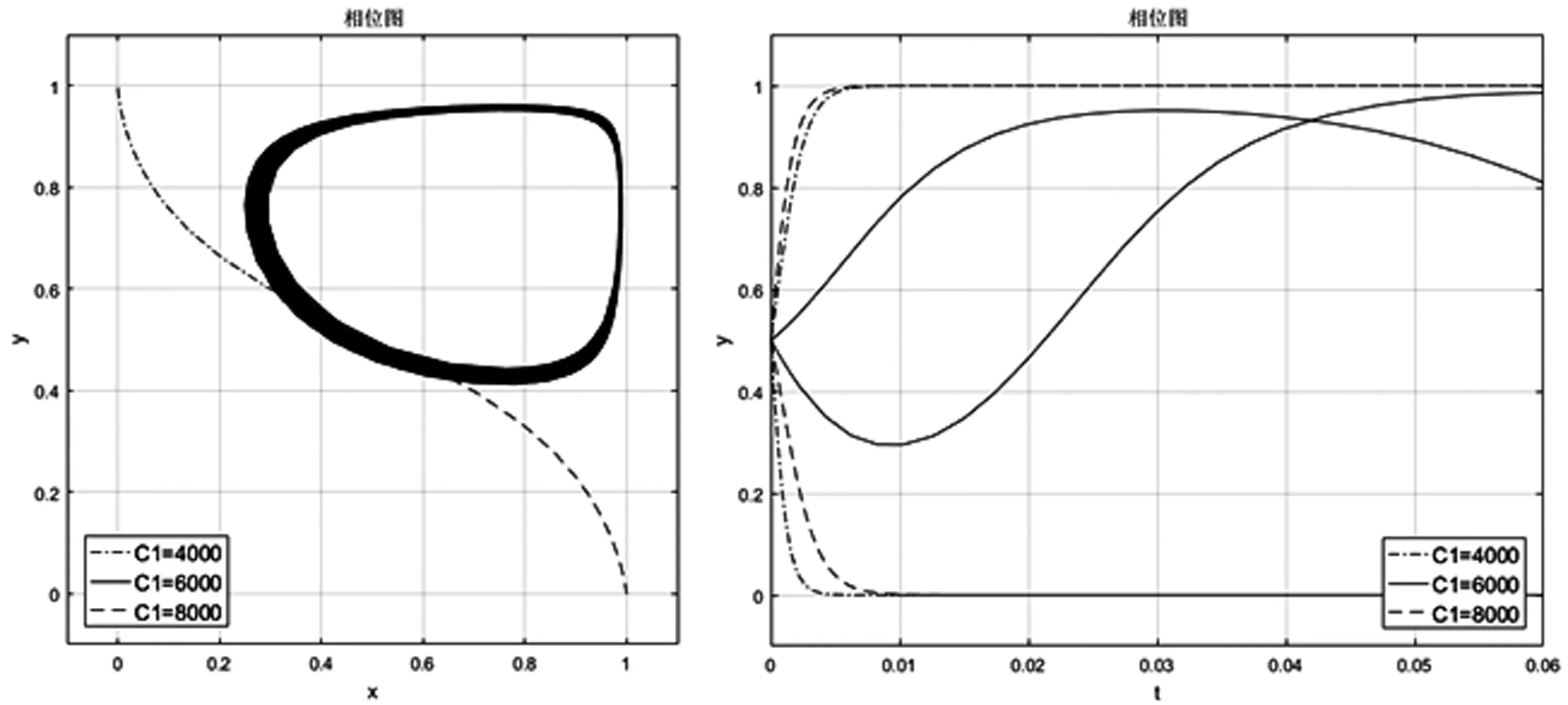
图7 C1值对稳定策略E(0,1)的影响

图8 θ值对稳定策略E(1,0)的影响

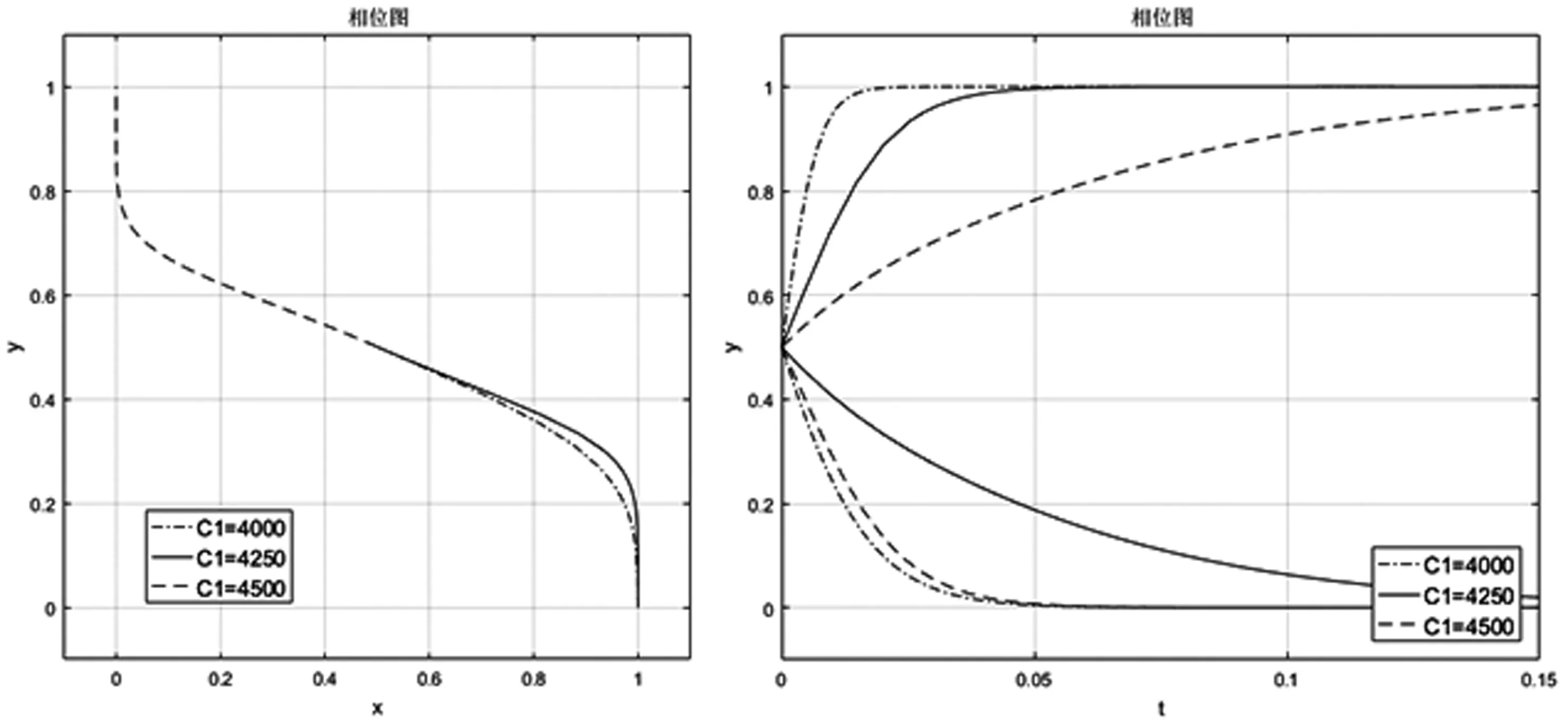
图9 C1值对稳定策略E(1,0)的影响

如果专利代理机构选择增大首付款比重(C1)的方式来减少违约损失，例如将C1从4000提升至4500时，此时稳定策略将从E(1,0)逐渐演化为E(0,1)，如图9所示。值得注意的是：稳定策略虽然离开“违约”，但也同时使预期收益分配模式不具有吸引力，双方更倾向使用传统模式，使均衡远离最优解决方案；同时，过高的首付款比重会导致系统寻找均衡解变慢，在现实专利代理实务中，参与者之间的博弈次数是有限的，过慢的均衡过程影响了稳定策略的达成。

当技术发明人选择违约时，提高违约罚款是否能够产生约束效果？仿真结果表明，等量提高M1和M2时，两者差值不变，对动态复制方程带来影响相互抵消，对演化稳定策略没有影响；而当扩大M1和M2的差值，即当技术发明人在预期收益分配模式中需面对更大的违约处罚力度时，演化稳定策略将经由E(0,0)向理想策略E(1,1)演进，且处罚力度差距越大，越快抵达E(1,1)，如图10所示。

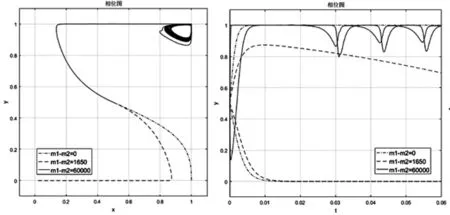
图10 M1-M2值对稳定策略的影响

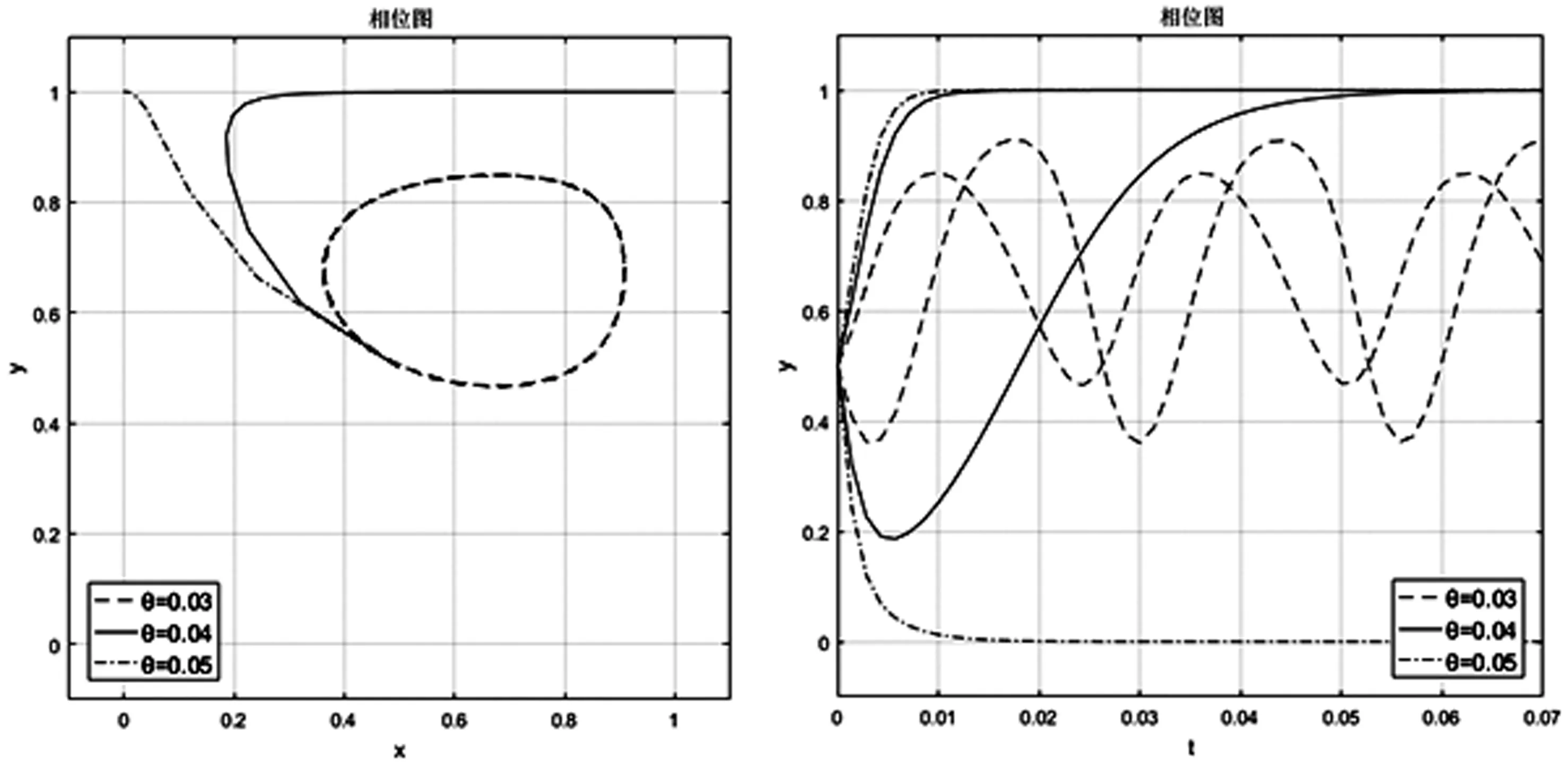
图11 θ值对稳定策略E(1,1)的影响

因此，为促使技术发明人履约，最佳调节手段为扩大M1和M2的差值。

(3)E(1,1)点稳定性的影响因素仿真分析

当ψ1<0、ψ2<0、ψ3≠0且ψ4≠0时，演化博弈系统稳定点为E(1,1)，博弈双方的稳定策略为“预期收益分配模式”和“履约”，这一稳定点是博弈中的理想情况，此时双方能够在履约的基础上达成更有效的利润分配方式。但这种稳定策略容易受到预期收益分配模式初始条件影响。如图11所示，当C1=7000，C2=6000，C3=6000，θ=0.04，t=0.3，p=0.3时，系统稳定点为E(1,1)。此时，当θ值增大时，技术发明人的策略不变，仍然选择履约，而专利代理机构的稳定策略演变为“传统模式”；当θ值减小时，均衡消失。由此可知，降低专利预期收益分成会破坏合作关系，此举并不能使技术发明人获益。

如图12所示，当C1升高时，博弈稳定策略调整至E(0,1)，即双方放弃预期收益分配模式；当C1降低时，博弈均衡被打破，并逐渐在E(1,0)处建立新均衡，此时技术发明人的策略选择为“违约”。可见，E(1,1)点处代理费用对稳定策略的影响较为明显。

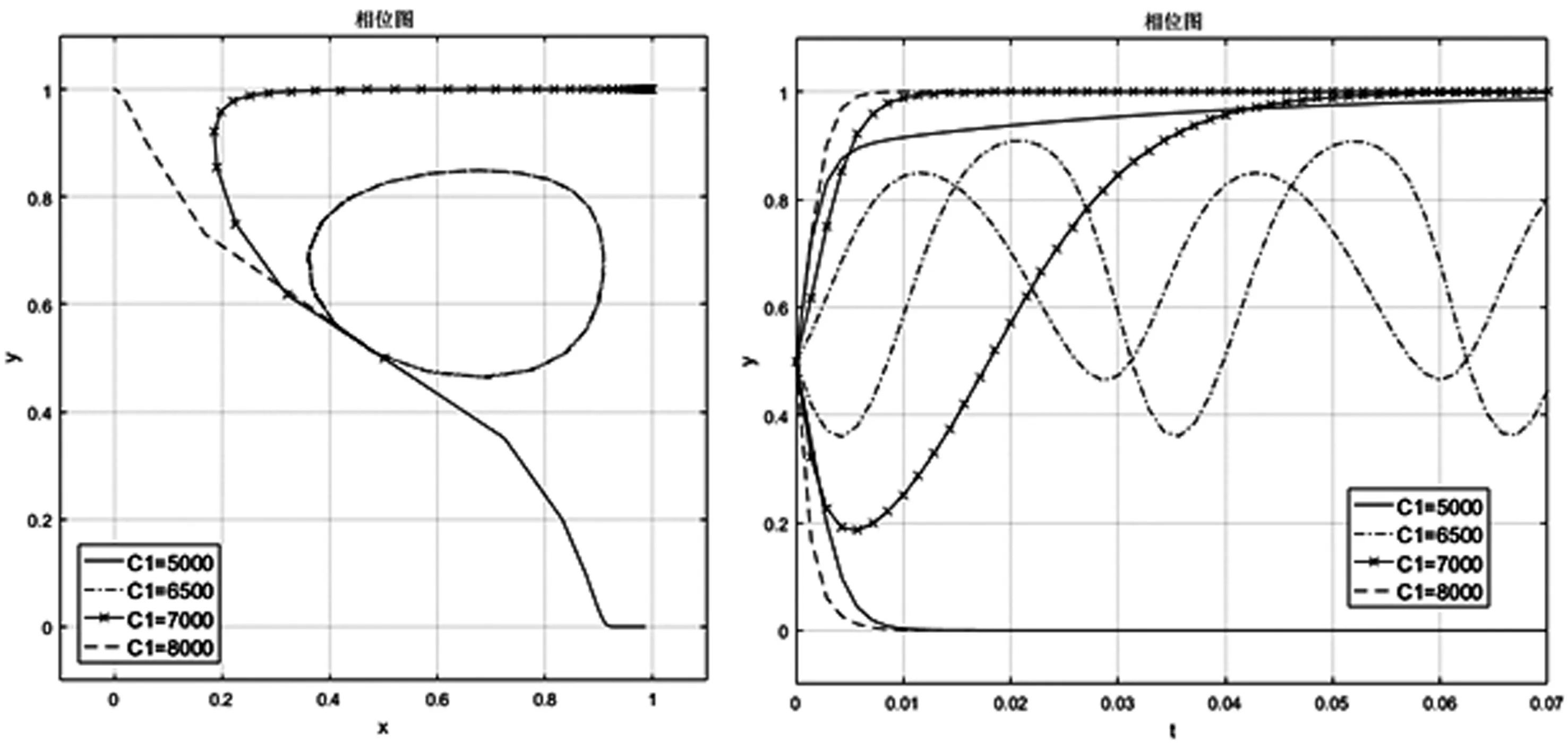
图12 C1值对稳定策略E(1,1)的影响

仿真分析揭示了演化稳定策略对初始参数不同的敏感程度：①预期收益分配模式易导致违约，而当专利代理机构对违约问题处置不当时，会导致稳定策略转向传统模式；②当出现违约时，提高预期收益分配模式下预期收益比重或增大首付款比重可使违约消失，但同时稳定策也会脱离预期收益分配模式；当提高预期收益分配模式和传统模式下违约罚款金额的差距时，博弈稳定策略则会倾向于向履约的预期收益分配模式移动；③在履约的传统模式稳定策略下，减小预期收益分成比重可有效促成预期收益分配策略的达成，且不会出现违约行为，而提高预期收益分配模式中首付款额会促使技术发明人选择违约。

4 结论

本文结合前景理论与演化博弈理论，引入有限理性主体的损失规避、收益偏好以及概率认知偏差特性，通过对模型的求解和仿真，获得双方达成共赢契约的约束条件和敏感变量，对优化专利代理服务模式起到一定的启示作用。研究结果表明：

(1)演化博弈的稳定策略有：①专利代理机构选择预期收益分配模式，且技术发明人选择违约；②专利代理机构选择预期收益分配模式，且技术发明人选择履约；③专利代理机构选择传统模式，且技术发明人选择履约。初始条件差异通过改变博弈参与者的主观感知，进而对四种边界条件产生影响，间接影响稳定策略。

(2)对模型的求解和仿真表明，预期收益分配模式具有可行性，恰当的引导可以实现对专利代理服务参与者的合作激励，有助于提升合作效率。同时，更少的预期收益分成比重，可促使合作更快达成。最后，为解决专利代理服务中的违约问题，通过区别设置预期收益分配模式和传统模式的违约处罚力度，例如单独增加预期收益分配模式中的违约处罚力度，可有效促使技术发明人减少违约意愿，维持长期稳定合作。