基于确定性系数组合模型的区域滑坡敏感性评价*

杨 光 徐佩华 曹 琛 张 文 兰志广 陈俊淇 董秀军

( ①吉林大学建设工程学院 长春 130026)

( ②成都理工大学 成都 610059)

0 引 言

滑坡敏感性评价是以地质环境条件为基础，参考滑坡现状静态因素预测滑坡在一定区域内发生的可能性大小( 倪化勇等，2015) 。近年来，3S 技术快速发展，许多研究人员将其应用于滑坡敏感性制图( Bai et al.，2009) 。地质灾害敏感性评价主要可以分为定性和定量方法两类，定性方法是以专家的知识和经验为基础来判断各个因子的权重，然后将各个因子叠加，就得到了敏感性分区图; 近10 年来，定量分析方法逐渐成为地质灾害评价的主要方向。定量方法是使用一种或多种数学方法来分析地质灾害的数据与选取的评价因子是否具有相关性，然后叠加各因子得到敏感性分区图。常用的分析方法有层次分析法( 许冲等，2009) 、模糊综合评判法( 王哲等，2012) 、逻辑回归法( 陈燕平，2010) 等。其中层次分析法和模糊综合评判法是启发式方法，逻辑回归方法属于统计方法，统计方法具有较高精度并且能够客观评价因子的权重，因此确定性系数法( 许冲等，2010; 刘丽娜等，2014; 冯杭建等，2017) 、信息量法( 许英姿等，2016; 寇丽娜等，2017) 等统计方法已经广泛应用于地质灾害评价。除了统计方法，大量机器学习算法如支持向量机( Chen et al.，2016) 、多层感知器模型( 王志恒等，2015) 、决策树模型( Tsangaratos et al.，2016) 等也被广泛使用。但是单一的评价模型会存在一定的缺点，例如确定性系数法没有考虑每个评价因素对地质灾害敏感性的影响差异，而层次分析过程不能考虑每个因素内不同特征变量对其的影响，逻辑回归法和多层感知器法无法解决各个影响因子的量化问题，即多源数据类型的合并问题，难以客观、定量准确地进行区域地质灾害评价。基于此，近些年组合方法得以广泛的应用并取得良好效果，像信息量法与Logistic 回归法组合( 樊芷吟等，2018; 张晓东等，2018) 、支持向量机和人工神经网络组合方法( 夏辉等，2018) 。

确定性系数方法计算严密，可以解决多源数据类型的合并问题，也能够很好地解决影响因子内部不同特征区间对地质灾害敏感性的影响; 层次分析法可以很好地考虑每个因素的复杂性以及不同因素对地质灾害敏感性的影响差异; 逻辑回归模型属于统计方法，计算简单，物理意义明确，可以用简单的线性回归来描述自然现象之间复杂的非线性关系;多层感知器是数据挖掘方法，具有突出的非线性映射能力更适合用于滑坡预测预报。将确定性系数分别与层次分析法、逻辑回归模型、多层感知器模型结合进行滑坡敏感性评价，结合各个模型的优点，能够较好地解决使用单一模型在地质灾害敏感性分析中的不足，使评价结果更为直观合理。

为了对研究区的土地利用规划及防灾减灾预警工作提供一定的参考，本文结合122 个灾害点，对四川茂县叠溪镇到石大关乡区域的地质灾害敏感性进行评价。在茂县的孕灾环境基础上，选取了坡度、剖面曲率、起伏度、坡向、距河流距离、高程、地层、距断层距离、土地类型、植被覆盖度10 个影响灾害发生的评价因子，并选用确定性系数( Certainty Factor，CF) 法分别与层次分析( Analytic Hierarchy Process)法、逻辑回归( Logistics Regression，LR) 法、多层感知器( Multiple Layer Perceptron，MLP) 法相结合等3种方法对区域进行敏感性区划，比较3 种模型的敏感性分区效果。

1 研究区概况

研究区为叠溪镇到石大关乡区域，位于四川省茂县东北部，地理范围在103°32' ～103°51'E，31°48'～32°12' N 之间( 图1a) ，面积为1120 km2。研究区地处青藏高原向川西平原过渡地带，北侧有岷山、南侧有龙门山、西侧有邛崃山等山脉。研究区为中山地带，地貌以高山峡谷为主，地势由西北向东南倾斜，高程最低为1581 m，最高为4711 m，相对高差3130 m( 图1b) 。研究区属高原性季风气候，垂直气候和地区气候明显，海拔超过2400 m 的地区气温低，海拔低于2400 m 的地区气候温和，年均气温11.0 ℃，夏季和秋季降雨较多，春季和冬季降雨较少，年降水量486.3 mm; 研究区内河流属岷江水系，支流发育，迂回曲折，纵贯全境，境内流长约5 km。区内出露的地层主要有三叠系、二叠系、泥盆系、志留系，岩性主要为早三叠系灰绿色变质凝灰质砂岩、粉砂岩与绢云板岩，中夹薄层灰岩，为软硬互层; 中三叠系变砂岩、板岩，夹灰岩，为软质岩体;晚三叠系深灰色薄－厚层变质长石石英砂岩、含砾砂岩，与炭质板岩互层，为软质岩体; 二叠系碳酸盐岩夹硅质岩，为硬质岩体; 泥盆系灰黑色变质泥、砂、炭硅质岩，夹碳酸盐岩，为软质岩体; 志留系绿色绢云板岩，夹砂质灰岩、石英砂岩，为软质岩体。研究区的断裂和褶皱较为发育，区内主要断裂构造为岷江断裂和松坪沟断裂( 图1c) 。这些断裂和褶皱造成区内岩体破碎，产状倒转等特点，大部分属马尔康地质分区。

2 研究方法

2.1 CF-AHP 模型

确定性系数法是一种概率函数方法，用于分析影响事件发生的各种因素的敏感性。基本假设条件为:滑坡灾害的易发程度可依据以前发生的滑坡与确定为环境因素的数据集之间的统计关系来确定。Shortliffe( 1975) 提出确定性系数模型，并经过Heckerman( 2013) 修正。确定性模型可以组合不同类型的数据，它可以有效地解决数据输入的异质性和不确定性，数据处理和评估过程相对简单，准确性高。因此，它被广泛用于滑坡敏感性评估。模型假设将来发生地质灾害的条件与以前相比是不变的，

计算公式为:

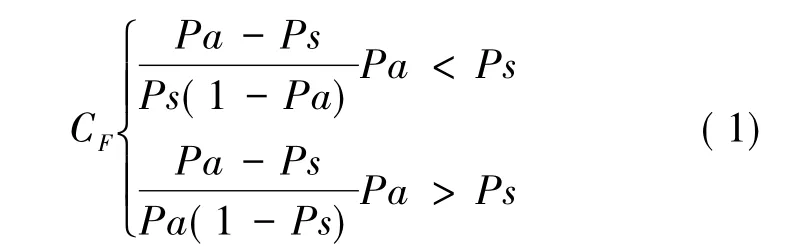
式中，CF为地质灾害的确定性系数; Pa 为影响因子数据a 中地质灾害个数与数据a 面积之比; Ps 为研究区灾害总个数与研究区总面积之比。由式( 1) 可知，CF区间为［－ 1，1］，CF越接近1，说明地质灾害发生的确定性越大，对应区域极有可能是灾害易发区; CF越接近－1，说明地质灾害发生的确定性越小，对应区域是灾害易发区的可能性很小。

层次分析法是一种定性与定量相结合的系统化决策方法，由美国学者Saaty( 1980) 在20 世纪70 年代提出。它的基本原理是根据问题的实质，将决策问题的有关元素分解成指标等层次，按照指标之间的相互关系进行组合，形成一种定性与定量关系相结合的多层次递阶结构。层次分析法可根据以下几个基本步骤来进行: ( 1) 首先应该建立起递阶层次结构模型，通过分析问题所选取的指标及指标之间的相互关系确立; ( 2) 从层次结构的第2 层开始，采用1～9 标度方法，根据萨蒂方法，比较每个因素，构造判断矩阵; ( 3) 根据层次分析法的基本原理，应该满足判断矩阵A:

式中，ω 为对应于矩阵A 的最大特征值λmax的特征向量，并引入一致性指标CI 来测量判断矩阵的偏离，检验一致性。

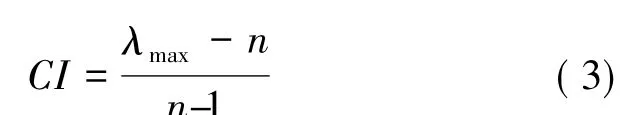
引入平均随机一致性指标RI，其值如表1 所示。随机一致性之比CR 为:

如果CR＜0.1，则判断矩阵满足一致性检验，因子权重设定指标较合理。

表1 随机一致性指标(RI)Table 1 Random consistency indicator( RI)

CF-AHP 组合模型是利用AHP 计算所选取指标因子的重要性程度，并且采用CF 法计算不同因子的CF 值，并此为基础，将指标因子的CF 加权求和，得到要评价的区域的敏感性指数，以此为依据进行研究区敏感性评价。

2.2 CF－LR 模型

逻辑回归模型是研究二分类因变量常用的多元统计分析方法，其中因变量y 只取两个值，在地质灾害分析中，y 通常会取值0 和1( 0 代表地质灾害不存在，1 代表地质灾害存在) 。模型用来描述二元因变量和一系列的自变量( X1，X2，…，Xn) 之间的关系。自变量数据类型没有具体要求，逻辑回归模型具有容易计算，物理意义明确等优点，可以用简单的线性回归来描述自然现象之间复杂的非线性关系，也可以用来预测事件发生的概率。逻辑回归估计的优势比也可以用来检验自变量与因变量之间的相关性强度。该方法在滑坡敏感性分析中得到了广泛的应用。函数如下式:

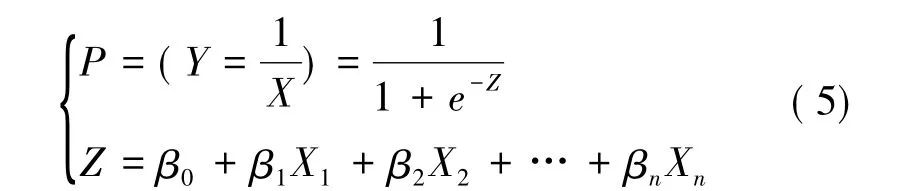
式中，P 为滑坡可能发生概率，在［0，1］区间，β1为通过计算得到的回归系数。

CF－LR 组合模型是将由确定性系数模型计算出的各个指标等级的CF 值作为逻辑回归模型中的指标值，不同滑坡点处和非滑坡点处提取CF 值，建立回归方程以估计逻辑回归系数，以此为依据进行研究区敏感性评价。

2.3 CF-MLP 模型

Rumehart 等提出了多层感知器模型( Multiple Layer Perceptron，MLP) ，它可以解决单层感知器模型存在的非线性可分数据的多类别分解问题，多层感知器是一种按照单向误差传播的多层前馈网络模型，相对于一般的线性统计方法，多层感知器突出的非线性映射能力更适合用于滑坡预测预报，因此，多层感知器模型在滑坡敏感性分析中得到广泛的应用，是最基本的网络模型之一。

MLP 模型由3 部分组成，分别为感受层( S) 、联想层( A) 和响应层( R) 。3 部分都是由同类的神经元构成的，特征向量通过感受层输入，联想层属于模型中的隐含层，而响应层为网络的输出层。模型示意图如图2。

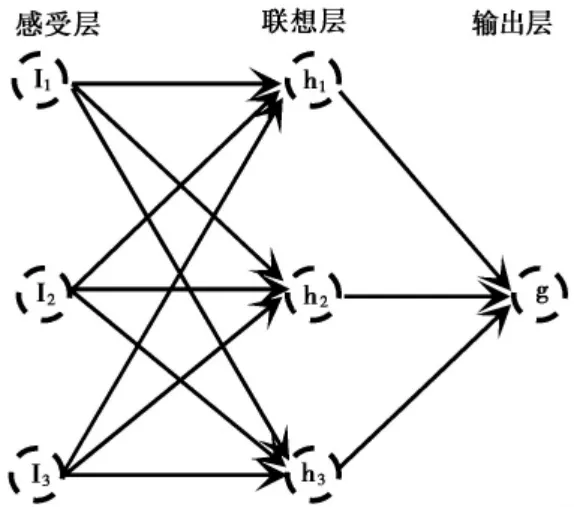
图2 MLP 模型示意图Fig. 2 MLP model diagram

CF-MLP 模型通过影响因子的CF 值来确定滑坡的关键影响因子，每个影响因子的CF 值都位于相同的数据区间。此数据具有同样的量纲，解决数据类型的合并问题。CF-MLP 模型将CF 值通过输入层输入，结合CF 函数和MLP 模型，构建出CFMLP 模型，很好地提高了模型的精度。

3 评价因子的选择和分级

本文选取244 个样本点，其中滑坡点和非滑坡点分别为122 个，从244 个样本点中随机选择70%的数据作为训练样本来建模，再结合本文选取的10个评价因子，采用CF-AHP、CF－LR 和CF-MLP 3 种模型评价研究区的滑坡敏感性并分区，利用剩余的30%样本点，采用精度检验，结合滑坡实际发育情况讨论并比较3 种模型。

有许多影响滑坡发生的因素，指标的选取主要基于前人对滑坡灾害的研究( Park et al.，2012) ，Park et al. ( 2012) 对2005～2012 年发表的220 余篇文献进行总结，统计出一些常用影响因子，结果如图3。根据研究区的地质灾害调查资料，并结合上述统计结果，经过分析选择坡度、剖面曲率、起伏度、坡向、距河流距离、高程、地层、距断层距离、土地类型、植被覆盖度10 个因子作为研究区的评价因子( 图4) ，每个因子的分级指标见表2，指标数据精度见表3。

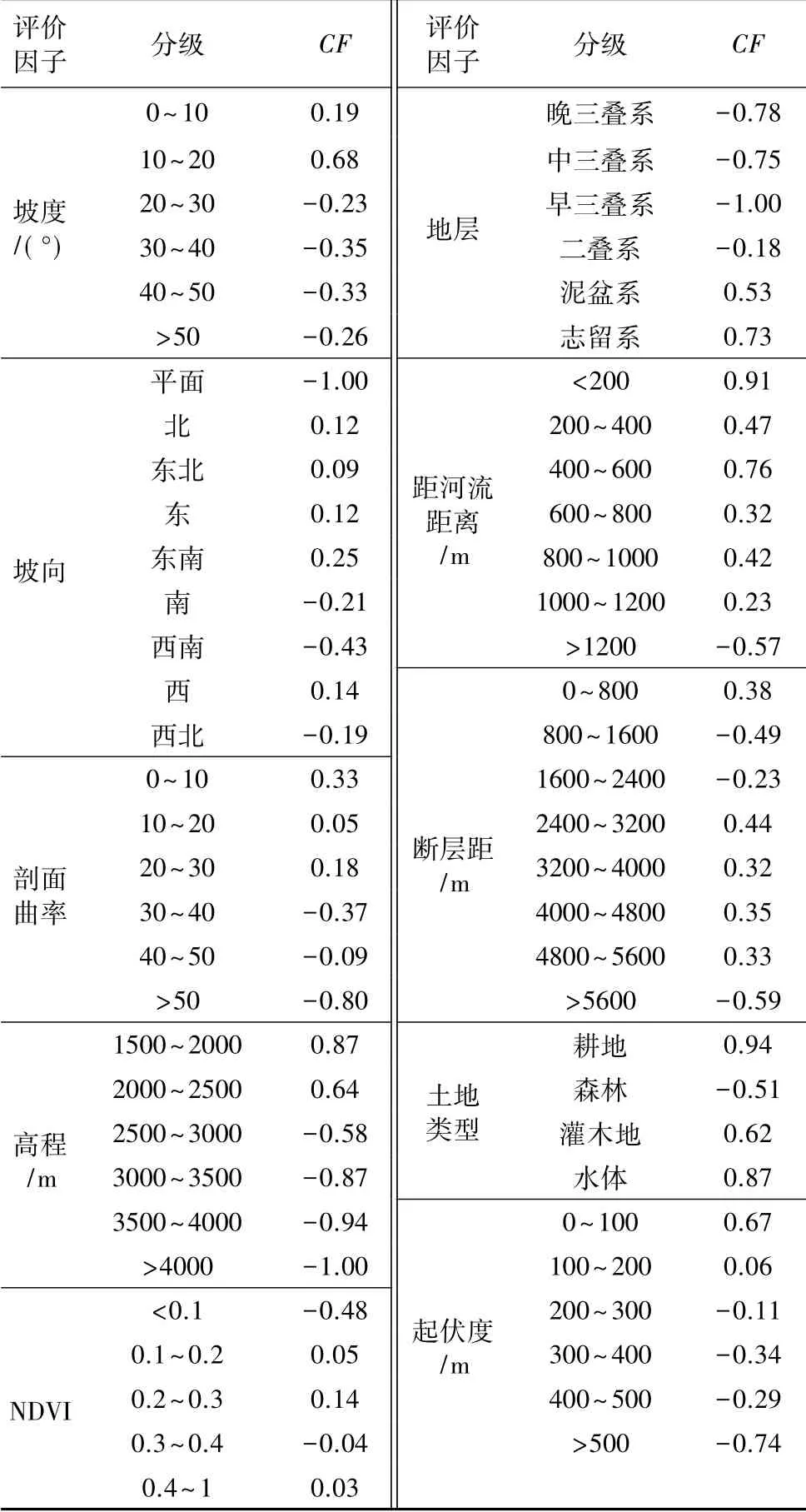
表2 各评价因子分类级别确定性系数计算结果表Table 2 Results for different classes of influence factors of CF model

图3 滑坡影响因子文献统计( Park et al.，2012)Fig. 3 Landslide impact factor literature statistics( Park et al.，2012)

图4 研究区滑坡敏感性评价因子Fig. 4 Conditioning factors for landslide hazard assessment of the study area

高程是滑坡发生的重要影响因素，对坡体应力值大小起着重要影响，坡高越大，应力值也越大，影响滑坡的势能。研究区地处高山峡谷地区，高程对降雨、植被分布特征及土地利用范围都会产生重要的影响，因此有必要对高程因素进行考虑; 滑坡通常都会发生在一定的斜坡上，在一定坡角范围内，由于坡角的增大，边坡的破坏概率增加，因此坡度对滑坡发生起着重要的作用; 坡向不同会影响滑坡环境的植被覆盖率、降雨量的大小，也会对岩石风化节理发育程度造成影响; 剖面曲率描述了斜坡形状的形态特征，反映了地表侵蚀和地表径流的形成，例如凸型坡非常容易在坡脚处发生应力集中导致失稳，安全性十分不好; 地形起伏度可以反映坡面的变化，可以揭示整个区域的地形变化规律; 通常来讲，起伏度越大，地形内的地势变动也就会越大，研究区处于高山峡谷地区，地势变化比较明显，因此对起伏度进行考虑。植被覆盖情况是区域地质灾害发育的重要影响因素，植被可以对滑坡的稳定性起到积极的作用，滑坡多发生在无植被或低植被覆盖的区域，NDVI 是反映植被覆盖度的常用指标，NDVI 值越大，植被覆盖越好。地层岩性对滑坡的发生有明显的影响，例如出现强度较差、结构破碎等情况的地层就十分容易发生滑坡( 尚敏等，2018) ; 边坡的类型、硬度、结构特征等对边坡的物理力学性能、变形性和破坏模式有很大的影响; 河流两岸的坡度通常由河流侵蚀，在正常情况下，与河流的距离越近，侵蚀越强烈，滑坡的发生概率越高( 谭春，2013) ; 断层距离是滑坡发生的重要影响因素，构造带发育的地方容易发生滑坡，因为断裂带岩石相对破碎，节理断裂发育，岩石强度明显降低，使该地区边坡不稳定，更易发生滑坡。

表3 影响因子信息数据Table 3 Impact factor information data

4 滑坡敏感性评价结果

4.1 结 果

4.1.1 CF-AHP 模型

根据前人的研究( Pourghasemi et al.，2017) ，利用层次法将指标进行对比，将每个指标赋值1～9，赋值越小，则对应的权重就越大，构建判断矩阵获取各指标权重，如表4 所示。CF-AHP 模型因子权重由大到小依次为地层、断层距、坡度、河流距、土地类型、高程、坡向、剖面曲率、NDVI、起伏度。

4.1.2 CF－LR 组合模型

将122 个样本点10 个因子的CF 值作为数据源，在SPSS 软件中进行二项逻辑回归分析，其中每个评价因子的CF 值都是独立的自变量，将滑坡是否会发生作为因变量，回归分析结果( 表4) ，从左到右依次为变量系数值( B) 、B 的绝对值和重要性排序。

选用回归系数的绝对值作为分析因子重要性程度的指标，该因子对滑坡发生的影响随着绝对值的增大而增加。各因子回归系数B 的绝对值如表5所示。可以看出，CF－LR 模型计算出的因子权重由大到小依次为高程、距断层距离、地层、土地类型、坡度、剖面曲率、NDVI、坡向、地形起伏度、距河流距离。

表4 层次分析法判断矩阵与各因子权重值Table 4 Analytic hierarchy process judgment matrix and each factor weight value

表5 逻辑回归分析结果Table 5 Results of logistic regression analysis

将以上10 个因子数值代入到逻辑回归计算模型，得到研究区逻辑回归式( 6) :

式中，P 为发生滑坡的概率; x1－ x10分别为NDVI、河流距、断层距、坡度、坡向、剖面曲率、土地类型、地形起伏度、地层岩性、高程的CF 值。

4.1.3 CF-MLP 组合模型

基于影响因子的确定性系数和滑坡数据，构建多层感知器网络，其模型示意如图2 所示。基于MLP 网络训练得到各个影响因子的重要性系数( 表6) 。可以看出，CF-MLP 模型计算出的因子权重由大到小依次为高程、地层、坡向、坡度、起伏度、距河流距离、剖面曲率、土地类型、NDVI 和距断层距离。

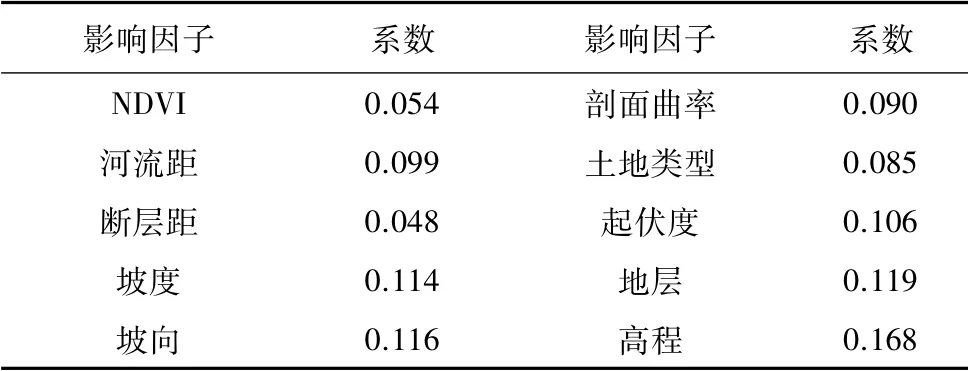
表6 影响因子重要性系数表Table 6 Impact factor importance coefficient table

通过上述3 种方法并结合ArcGIS 工具箱叠加计算出3 种模型的敏感性程度值，可以根据ArcGIS软件的自然断点法进行分级，自然断点法是统计学中常用的分级方法，能够保持类别的一致性，是一种比较客观的分类方法，在地质灾害分级中得到广泛应用( 谭春，2013) 。将研究区的敏感性分为4 级:高敏感性、中敏感性、低敏感性、极低敏感性。结果如图5。

CF 模型中，高、中、低和极低敏感区面积分别为144.29 km2、230.47 km2、340.08 km2和386.93 km2，分别占研究区总面积的13.0、20.9%、30.9%和35.2%; CF－LR 模型，高敏感区、中敏感区、低敏感区和极低敏感区面积分别为 124.95 km2、278.74 km2、248.17 km2和449.90 km2，分别占研究区总面积的11.3%、25.1%、22.5%和41.1%; CFMLP 模型，高敏感区、中敏感区、低敏感区和极低敏感 区 面 积 分 别 为 152.46 km2、191.99 km2、303.28 km2和454.04 km2，分别占研究区总面积的13.8%%、17.3%、30.0 和38.9%。高敏感区主要集中在石大关乡附近区域，沿着石大关乡到叠溪镇的岷江两岸也分布少部分滑坡高敏感区。

图5 研究区滑坡敏感性分区图Fig. 5 Landslide sensitivity map of the study area

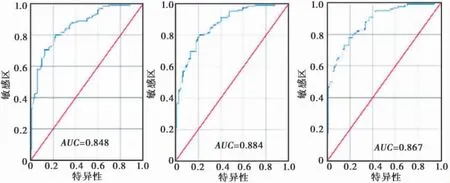
图6 3 种模型ROC 曲线图Fig. 6 ROC curves for three models

4.2 合理性检验

ROC 曲线是目前应用于地质灾害敏感区域评价精度验证比较常用的方法( Hamid et al.，2012) 。ROC 曲线非常简单直观，对所选用的方法和敏感性的关系能够很好的反映，试验的准确性非常好。AUC 表示ROC 曲线下的面积，其数值一般小于1，越接近1，说明模型模拟效果越好。

应用SPSS 软件，将3 种模型进行ROC 曲线的绘制，并求取AUC 值( 图6) 可知，3 个AUC 的值分别为0.850、0.884、0.867。其中CF－LR 模型AUC值为0.884，准确性最高，分区可靠。因此本区域选用CF－LR 组合模型。

4.3 结果分析

( 1) 地层:从表2 中可以看出，泥盆系和志留系CF 值为正值，这两个地层有利于滑坡的发生。这些地层的岩性为灰黑色变质泥、砂、碳硅质岩，夹碳酸盐岩和绿色绢云板岩，夹砂质灰岩、石英砂岩，都为软质岩体。岩体受水流冲刷作用影响很大，导致强度降低，岩体中常见弯曲和撕裂变形现象，因此，这些因素为滑坡变形提供了有利条件; 对于坡向，根据CF 值可以看出，研究区北、东北、东、东南和西向CF 值为正值，其中东南向CF 值最大，说明东南向最有利于滑坡的发生。边坡的坡向往往影响岩体的边坡结构，岩石反向边坡更容易发生弯曲，倾斜层质边坡比陡坡更容易发生滑坡; 对于土地类型和NDVI，根据CF 值，当土地类型为耕地和NDVI 区间为0.2～0.3 时最有利于滑坡的发生，当地区植被茂盛时，由于植被根系的作用，会加强边坡稳定性，没有植被的地区更容易引发滑坡; 断层距方面，滑坡主要发生在离断层0～3200 m 区间，在断裂带中，岩石相对破碎，节理断裂发育，因此更容易发生滑坡( Hong et al.，2015) 。

( 2) 图5 中敏感性高的地区大部分集中在主要水系周围、泥盆系和志留系的软质岩体、以及植被相对缺乏的地带，斜坡遭受水的冲刷，软化和动水压力将导致斜坡上的岩土强度下降，山谷两侧陡峭且起伏较大的斜坡，在地形的影响下容易发生滑坡。

5 结 论

( 1) 基于GIS 平台分析取得的敏感性评价结果，将研究区分成高、中、低和极低敏感区4 类。CF模型、CF－LR 组合模型和CF-MLP 组合模型中高敏感区分别占研究区总面积的12.2%、11.3% 和13.8%。滑坡高敏感区大部分集中在石大关乡附近区域，沿着石大关乡到叠溪镇的岷江两岸也分布少部分滑坡高敏感区，石大关乡应做好防灾工作。

(2) 研究区滑坡灾害敏感性评价结果表明高敏感区主要集中在主要水系周围与断层集中区域，其主要控制作用的因子是断层、高程、水系。

(3) 利用ROC 曲线，得到CF 模型、CF－LR 组合模型和CF-MLP 组合模型的AUC 值分别为0.848、0.884 和0.867。说明CF－LR 的组合模型在该研究区的滑坡敏感性评价中效果最好。采用CF－LR 组合模型所得出的敏感性分区图与研究区实际情况比较一致，可以为地质灾害风险评价提供参考。