基于混合结构数据的碳价格多尺度组合预测
任贺松,刘金培 ,郭 艺,郭 健
(1.安徽大学 商学院,安徽 合肥 230601;2.西安交通大学 管理学院,陕西 西安 710049;3.北卡罗莱纳州立大学 工业与系统工程系,美国 罗利 27695;4.东南大学 经济管理学院,江苏 南京 2111895;5.同济大学 经济与管理学院,上海 200092)
一、引 言
碳排放受到限制使各国开始重视低碳经济的发展。《京都议定书》和《巴黎协定》的签署使得低碳理念深入人心。目前欧盟等地拥有世界主要碳排放交易市场,其碳排放交易体系在解决气候变化问题方面有重要意义。2017年12月19日,我国的碳排放交易体系也正式启动。在此背景下,对欧盟等国际市场碳价的预测不仅有助于把握国际碳交易市场的价格走势,也有利于中国碳交易市场的健康发展。
碳价格序列是一种典型的非平稳 非线性时间序列[1]。最近研究表明,经验模态分解(Empirical mode decomposition,EMD)在处理此序列时具有良好的效果,EMD分解后的序列具有更好的尺度波动规律性,对分解得到的序列再利用合适的模型分别预测,具有更高精度[2-7]。李晓龙等应用EMD将航空公司旅客流量序列分解为多维度序列,结果表明,预测分解后的时间序列结果精度更高,优于传统的预测模型[2]。杨云飞等利用非线性原理,组合EMD和支持向量机(SVM)预测了原油价格。首先用EMD处理原油价格时间序列,将得到的分量根据频率的不同累加重构成3种时间序列,最后运用不同SVMs模型预测3个新序列并得出最终预测结果。就预测效果而言,此模型优于单项人工神经网络和SVM方法[4]。蒋铁军等基于进化核主成分回归(KPCR)和集合经验模态分解(EEMD)模型,应用自适应建模来预测多尺度复杂时间序列,发现该模型能有效描述时间序列在不同尺度上的变化趋势[5]。王书平和朱艳云从分解重构的思路出发,构建了一个包括SVM、EMD、人工神经网络(ANN)和时间序列方法的多尺度组合预测模型。LMF铜价经过此模型处理后得到高频、低频、趋势项三组时间序列并分别对其预测以此分析时间序列变化趋势的特点。实证分析表明,多尺度组合模型的预测精度高于各单项预测模型[6]。高杨等基于ICE碳排放期货交易所碳期货价格相关数据,先使用粒子群算法(PSO)-支持向量机(SVM)模型初步预测碳金融国际市场价格,再运用EMD模型,根据频率由高到低将误差序列分解成若干不相干、频率不同的本征模函数(Intrinsic Mode Function,IMF)和一个残差项,并分别进行预测效果比较显著[7]。
随着网络技术的不断发展,非结构化数据对于股票价格、房地产价格和碳价格等领域的预测作用引起人们的关注。孙毅等利用人们在网络社交媒体中的“行为”数据构建新型消费者信心指数(CCI),结果表明新型CCI的预警能力优于传统的CCI[8]。沈苏彦等基于“谷歌趋势”针对餐饮、住宿、出行等环节搜索了旅游相关的关键词,利用相关系数找出入境外国游客数量相关关键词,在对其构建自回归积分滑动平均模型(ARIMA)模型时加入带搜索关键词的自变量,并将此模型与未加入搜索关键词的ARIMA模型对比,结果表明,前者预测精度更高[9-10]。刘涛雄和徐晓飞在预测宏观经济指标时,以百度指数为例研究了网络搜索指数的作用,事实证明考虑网络搜索指数的模型有更准确的预测结果[11]。陈涛和林杰在研究网络舆情热度时空演变情况时就某一事件比较百度指数和谷歌趋势在空间时间关注度的变化特性,结论说明了关注度指标能够有效反映网络舆情变化情况[12]。王娜在预测碳价格时选用网络结构和媒体指数等非结构化数据并构建了网络结构自回归分布滞后(ADL)模型,实证分析表明加入了非结构化数据的网络结构ADL模型的预测精度更高,更适用于大数据预测[13]。
从已有研究来看,对于碳价格这种非线性非平稳结构较为复杂的数据一般运用EMD对其处理,再组合各序列预测的结果,以此降低预测误差。然而已有研究仍然存在两个问题:1.原数据经 EMD分解后,在分别预测重构得到的高频,低频和趋势项时仅用到一种单项模型,并未根据高频,低频和趋势项的特点选择对应方法。实际上,利用 EMD 将时间序列分解后,各序列对应的尺度波动特征存在差异,若采取同一种方法进行预测,往往会导致适应度较差,因此最终预测结果的精度也会受到影响[14]。2.已有的碳价格组合预测模型并未考虑非结构化数据的影响,在涉及到非结构化数据研究的文献中,预测碳交易价格主要用到的均为单项预测方法,而且也没有考虑非结构化数据不平稳的特性。
因此,为了综合利用多源信息,考虑到碳价格并非平稳和非线性的特点,本文提出一种基于混合结构数据的碳价格多尺度组合预测方法,并将其应用于欧盟碳价格预测。首先,从谷歌指数提取碳价格相关的非结构化数据并对其进行降维处理。然后,通过EMD对影响因素结构化数据、降维后的非结构化数据、碳价格逐一进行分解,并对得到的IMF利用Fine-to-Coarse reconstruction算法重构得到高、低频序列和趋势项。进而分别运用ARIMA,偏最小二乘(PLS),BP神经网络进行预测。最后,将单项预测结果组合得到最终预测结果,以此提高预测精度。
二、 多尺度组合预测模型
(一) 多尺度组合预测
本文首先利用主成分分析处理非结构化数据信息,将降维后的非结构化、结构化数据以及碳价格分别用EMD分解为多个具有不同频率的 IMF,并运用 Fine-to-coarse方法将其重构为高频、低频、趋势项,然后,分别用ARIMA,PLS,神经网络模型进行预测,预测模型流程如图1所示。其中,ARIMA针对时间序列本身找出内部规律并进行预测,无需考虑影响价格波动的因素;而PLS和神经网络则考虑多种影响因素并将其分别作为自变量,为增加预测精度,将谷歌指数非结构化数据与其他结构化数据一并作为影响碳价格波动的自变量,将碳价格序列作为因变量进行预测。最后,将预测的高频,低频和趋势项还原成原价格序列,从而实现整个预测过程。为了判断结果的精度,采用了正则均方误差(NMSE)、Theil不相等系数、平均绝对百分误差(MAPE)作为评估标准,并利用方向对称值(DS)评估模型对碳价格变化趋势的预测能力。
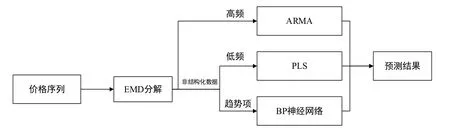
图1: 碳价格多尺度预测模型
(二)研究方法
1.EMD方法原理
1998年,Huang提出新的方法处理信号,即经验模态分解(EMD),它能将非平稳信号处理成平稳信号[15]。EMD是在对本征模函数(IMF)定义的基础上进行的。IMF具有两个特征,即它的零点数和极值点数差值不大于1,同时分别由局部极小值点和极大值点构成的下包络线和上包络线的均值为零。EMD能从信号中逐级提取出多个不同尺度的本征模函数,剩余的分量则代表原始信号的总体趋势。具体分解步骤如下:
(1)对于原始函数x(t),求出x(t)的所有极大值与极小值。使用三次样条函数拟合x(t)的包络线,并求出上、下包络线的平均值m11(t)。
(2)求原数据剔除低频的新序列h11(t),即

(3)用h11(t)替换上式中的x(t),重复上述两步,当h1(k-1)(t)与h1(k)(t)的方差低于设置的固定值时,可认为是h1(k)(t)一个IMF分量,即

(4)对r1(1)重复上述操作,可得到c2和r2(1)。不断重复操作,当rn(1)不能再分解时可得到分解后的s(t)形式,如下所示:

2.Fine to Coarse reconstruction 算法介绍
Fine to Coarse reconstruction算法能够将EMD分解得到的多个IMF重构成高频分量和低频分量,用ci(t)表示第i个IMF,r(t)为残差项[16]。
(1)计算前i个IMF的和
(2)计算si的均值,在确定显著性水平α的前提下,利用t 检验找出离零点最远的si均值点。
(3)如果si的均值点显著远离零点,将c1到ci加总,作为高频部分;将c1到ci加总,作为低频部分。
3.单项预测模型
自回归求积滑动平均模型(Autoregressive Integrated Moving Average Model)是时间序列分析的重要方法之一,可通过对数据进行拆分从而使其平稳化,基于此可精准预测EMD分解后的数据[17]。ARIMA由自回归模型(AR)和移动平均模型(MA)模型组成的,I代表拆分。模型的一般公式如下:

PLS能有效解决变量间多重共线性问题方面[18],它结合了主成分分析和典型相关分析等多种功能,建模时首先对数据进行标准化处理,然后不断提取PLS成分直至回归分析的拟合度达到预定标准。若未达标则进行迭代,如此反复至拟合度达标,进而得到高频预测值。
逆向传播误差算法可解决神经网络中连接各神经元的权重问题[19]。用BP神经网络对趋势项数据进行预测时,首先归一化处理数据,然后设置隐含层网络层数,最后确定每层的神经元数,即完成模型建立。将非结构化数据降维-分解-重构后的趋势项和结构化数据分解-重构的趋势项作为输入,神经网络首先利用这些数据进行训练,接着利用训练完成的模型预测碳价格。
(二) 非结构化数据的处理
非结构化数据的重要特性是不规则、不完整,包含办公文档、图片图像、报表文本等各种格式的数据,由于非结构化数据在数据总量中所占比重很大,其本身蕴藏着大量有待挖掘的价值。目前国内外已有一些学者将非结构化数据应用到原油价格等波动较大的时间序列预测,结果显示加入非结构化数据后预测效果明显提升。其中,百度指数及谷歌趋势等网络舆情指数是非结构化数据可视化的典型表现,同时也是应用非结构化数据的一个较为理想的切入点。本文首先搜集若干谷歌指数,由于指数数据难以直接利用,故采取主成分分析法对其降维,再将得到的主成分数据作为非结构化因素与其它结构化因素一并作为碳价格影响指标,并逐一进行EMD分解以及对应的预测,如此便实现了应用非结构化数据的预期目标。
三、实证分析
(一)数据样本的选择
碳排放期货交易所(Intercontinental Exchange,ICE)是欧洲最大的碳交易机构,而欧盟碳排放额(European Union Allowance,EUA)是目前欧盟碳排放交易体系中交易量最大的期货之一,具有一定代表性,因此选取ICE的EUA期货价格作为预测对象。本文收集了2015年1月9日到2017年3月10日EUA期货交易的每周结算价格,共114个数据。图2曲线代表EUA合约期货周价格变化趋势。
本文选取了纽约商业交易所(New York Mercantile Exchange,NYMEX)天然气交易价格、ICE西德州中级原油(West Texas Intermediate,WTI)价格、标准普尔500指数,鹿特丹煤炭价格作为影响EUA合约期货价格的影响因素。其中,纽约商业交易所是世界较成熟的天然气期货市场;WTI对国际原油基础价格的制定有较强的影响;标准普尔500指数反映了美国股市整体的运行情况;鹿特丹煤炭价格是西欧煤炭市场交易商定价的重要参考标准。以上因素的数据均来自wind数据库。
为了从不同角度探究影响EUA合约期货价格因素,本文利用谷歌指数,搜索五个与碳交易相关的关键词,分别是carbon footprint、carbon price、carbon market、carbon trading、carbon sink,从搜索结果中提取了两个主成分,将这两个主成分作为非结构化数据纳入到影响因素范围中。

图2:EUA合约期货周价格变化趋势
(二)评价标准
通过运用平均绝对百分误差(MAPE)对模型的误差及预测性能进行评估,MAPE的特点是不对离差进行绝对值处理,避免出现数值的正负抵消,从而真实地反应预测效果和误差值情况[20]。分别采用方向对称值(DS)评估模型对碳价格变化趋势的预测能力,利用Theil不相等系数(U)来测量预测方法的精度。同时也使用均方百分比误差(MSPE),平均绝对误差(MAE)两个指标来更全面地评估模型预测能力。各指标定义如下所示:

其中,N是样本容量,Ri,Pi代表实际值和预测值,MAPE,MSPE,MAE,U的值越小,得到的结果越精确;DS的值越大,则表示模型效果越好。
(三)预测过程
用EMD处理114个样本数据,最终得到5个IMF分量和1个趋势项分量,结果如图3所示。其中IMF1-IMF5为5个本征模函数,res.为剩余分量。
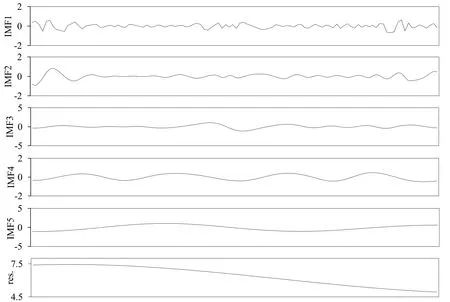
图3:碳交易价格EMD分解结果
采用Fine-to-Coarse技术将IMF分为高频部分和低频部分,分类原则为利用t检验判断第一个均值显著偏离0的IMF,将此IMF作为分界线,包括此IMF在内之前所有的IMF为低频部分,之后所有的IMF为高频部分。各IMF均值如下图所示,根据以上原则,可得出IMF1到IMF4为低频部分,IMF5为高频部分。对影响碳期货交易价格的6个因素用同样方法进行处理,可得到6组EMD分解值及6组高频部分和低频部分。

图4:碳期货交易价格分解各IMF均值
碳期货交易价格走势及用Fine-to-Coarse技术将各IMF分成的高频,低频和趋势项三个分量的走势如下图所示:

图5:碳交易价格及其各分量序列
(四)碳期货交易价格的预测和对比
对于碳期货交易价格的三个分量,分别用ARIMA,PLS,BP神经网络模型进行预测,然后将三者的预测结果加总后即得最终预测结果。三种方法的预测过程如下:
运用 ARIMA对低频序列进行预测,先对数据拆分使其达到平稳状态并最终选用 ARIMA(4,1,15)模型。运用PLS对高频序列进行预测,首先进行多重共线性分析,再利用SIMCA-P软件进行PLS回归分析,根据预测误差最小原则确定PLS成分个数为2个,据此对原序列进行预测。选用BP神经网络预测趋势项,对趋势项进行标准化处理后,确定此模型的输入层节点、隐含层神经元节点、输出节点数目分别为8个、6个、1个。将以上三种方法对不同时间序列的预测结果累加,即可得到最终的碳价格期货交易价格,并将其与实际值进行比较,如图6所示。
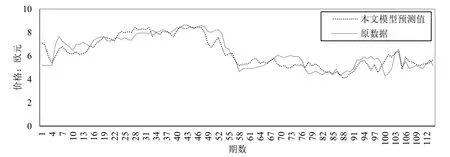
图6:碳期货预测值与实际值比较
(五)碳期货交易价格预测对比
为了验证本文中对多尺度碳期货交易价格预测的有效性,将构建的多尺度组合预测模型分别与EMD-ARIMA模型、EMD-PLS模型、EMD-BP神经网络模型的预测结果进行比较,同时为了验证EMD具有改进预测结果的特征,又加入了自变量不分解时对碳期货交易价格预测结果的比较。比较的结果如表1所示。

表1:碳交易价格预测效果比较
从表2可以看出,在此评价指标体系中,本文设计的碳价格多尺度预测模型对应的MAPE、U、MSPE、MAE的参数值均为最低,且DS数值最大,从而验证了本文设计的模型对碳价格预测效果最好,均优于其他模型。
通过对欧盟碳价格预测的实证分析,可以看出本文的预测方法有以下明显优势:
1.我们提出的碳价格预测模型有效利用了网络搜索指数非结构化数据和其它影响因素等结构数据,多源信息的有效利用提高了预测精度,也能更准确地判断碳价格的变化趋势。
2.我们在对碳价格序列及输入数据均进行EMD分解后,有效滤除了噪声信息,能够挖掘时间序列的深层次规律和波动特点。
3.根据输入信息和碳价格序列分解重构后不同频率数据的特点,有针对性的选择三种不同的预测方法,并将各方法预测的结果组合起来得到碳价格时间序列预测值,充分发挥了各单种方法的优势。
四、结束语
碳市场交易价格波动性较大,具有平稳性差、非线性的特点,针对现有研究没有充分考虑到非结构化信息的影响、多采用单一模型来预测碳市场的易价格、预测精度不高等问题,本研究在充分利用非结构化数据的基础上,建立了基于混合结构数据碳价格多尺度组合预测模型,并将其应用于欧盟碳价格预测。首先,提取碳交易价格相关的非结构数据和结构数据信息,用EMD方法将混合结构数据和碳期货交易价格分解为多个IMF分量和趋势项,再根据Fine-to-Coarse技术将多个IMF重构为高频分量与低频分量,最后分别用ARIMA,PLS,BP神经网络预测高频分量、低频分量、剩余趋势项,将预测结果组合得到碳价格时间序列预测值。在选择影响因素过程中,除选用其他能源价格外,本文创新性地引入了非结构化数据,同时为验证所提出预测方法的预测精度和有效性,比较了不同预测模型的结果。研究结果发现,与已有预测模型相比,本文构建的模型能够有效利用混合数据信息,显著提高预测的精度,适合国际碳市场交易价格的预测。

