基于签到数据和交通工具的多目标旅游路线推荐
(福州大学 经济与管理学院,福建 福州 350116)
引言
随着Web 2.0时代的到来,互联网技术和移动设备的快速发展,有越来越多的用户愿意在社交平台上分享自己的旅游经验,然而分享者越多,信息就会越膨胀。近年来,随着旅游业的蓬勃发展,越来越多的人会选择假期出游,一般情况下,用户新到一座城市游玩,首先会上网搜索该城市的旅游资讯来安排自己的旅程,而网络上的旅游信息量庞大又繁杂,用户要从这些数据中找到符合个人现实需求的有用信息是一件非常费时又费力的事情。现如今,随着时代的发展,用户的旅游消费观念也日渐理性化和个性化,景点的实际情况,如景点的类别、开放时间、票价、两个景点之间的转移时间和转移费用、是否对特殊人群(如:残疾人、老人、学生等)半价等,都会对用户是否去该景点游玩产生影响。因此,个性化旅游路线推荐具有重大的研究意义。
本文主要工作如下:
(1)提出了基于签到数据感知用户偏好和景点流行度的景点评分机制。
(2)将交通工具的选择这一因素纳入旅游路线推荐的考量之中。在本文中,我们考虑时间和预算两个约束条件,而选择不同的交通工具就会导致两个景点之间的转移产生不同的转移时间和转移费用,进而影响时间和预算约束。
(3)提出基于多约束多目标的剪枝算法,为用户推荐一条最优旅游路线。一般情况,在满足约束的前提下,用户都希望花尽可能少的钱游览尽可能多的类别不同且得分高的景点。
(4)以 Foursquare社交网站上的真实数据和马蜂窝上成都著名景点的信息作为数据集,验证了本文提出的推荐算法能够为用户提供更符合其需求的个性化旅游路线。
一、相关工作
在给用户进行旅游路线推荐之前,需要知道哪些景点对于用户而言是有吸引力的。一般情况下,景点得分越高,对用户而言就越有吸引力。有学者提出了基于时间的用户兴趣偏好,即用户对于某类景点的兴趣程度取决于该用户在该类景点所花费的时间,景点的得分由景点的流行度和用户兴趣偏好决定[1]。还有学者提出兴趣点得分由三部分组成:兴趣点的类型得分、兴趣点的类别得分和关键字搜索得分,一类兴趣点可以包含多个类别,某个兴趣点所包含的关键字占用户关键字搜索得越多、该兴趣点所属的类别在用户感兴趣的类型中占比越大,那么该兴趣点的得分就会越高[2]。还可使用加权类别层级(WCH)和迭代学习模型找到本地专家,从用户访问过的地理位置的类别中提取出用户的偏好,根据用户指定地理空间范围内的候选本地专家来匹配其偏好,最终,基于所选本地专家的意见推断候选位置的分数[3]。也可将旅游景点的特征与用户的喜好进行语义匹配,评估出用户偏好,并据此评估出可用的旅游景点[4]。
旅游路线推荐其实就是将兴趣点集通过时间序列串连起来,故了解兴趣点推荐相关研究是很有必要的。Ye等学者提出了融合用户对兴趣点的偏好、地理位置影响和社会影响的统一协同过滤方法[5]。Gao等学者将时间影响纳入矩阵分解的框架之中,针对不同时间间隙通过不同的潜在向量对每个用户建模,提出了LRT模型[6]。Lian等学者将地理位置影响纳入加权矩阵分解的框架之中,根据用户历史签到记录的空间聚集现象,提出GeoMF模型来模拟用户活动区域与地理位置之间的相关关系[7]。Liu等学者提出了一种基于加权矩阵分解的IRenMF模型,该模型考虑位置级别和区域级别的影响,认为用户对相邻的兴趣点有相似的偏好和同一区域的兴趣点可能共享相似的用户偏好[8]。还有学者结合了机器学习中的相关算法(如:监督学习)来向用户推荐兴趣点[9]。
旅游路线推荐的目的是为用户规划出一条或多条符合用户现实需求的个性化旅游路线。近年来,出现了大量关于旅游路线推荐的相关研究。在定向问题基础上,通过分析用户在社交网站上分享的旅游照片来获取景点的流行度和用户的兴趣偏好,根据给定POI集合,时间预算,起点和终点,为用户推荐一条满足时间预算且分数最高的路线[1]。提出解决AdditiveTour问题(尽可能多地为用户推荐得分高的景点)和CoveringTour问题(让用户尽可能多地访问不同类型的景点)的方案,为不同需求下的用户推荐旅游路线[10]。有学者利用照片共享站收集用户带地理标记的照片,使用均值漂移程序对照片进行聚类,通过马尔科夫模型和主题模型生成摄影师行为模型,用以估计摄影师访问地标的概率,从而生成旅游路线[11]。还可使用以特征为中心的协同过滤算法来对用户偏好建模,在假设两个POI之间的旅行时间是确定的情况下对POI可用性建模,在不考虑POI多样性的情况下对旅行时间的不确定性建模,以及根据LDA主题建模方法对POI多样性建模,综合考虑用户偏好、POI可用性、旅行时间的不确定性以及POI多样性来向用户推荐最优路线[12]。根据用户给定的查询位置、旅行时间约束以及用户对景点类别选择的集合,找到一条非重复多类别且收益最大化的最优景点访问路线[13]。
与上述工作相比,本文的主要工作有:提出了基于签到数据感知用户偏好和景点流行度的景点评分机制,将交通工具的选择这一因素纳入旅游路线推荐之中,提出了基于多约束多目标的剪枝算法,来为用户推荐一条最优路线。
二、基本定义
为了方便阐述所要解决的问题,定义了一些符号和公式。
定义1景点信息。对于每一个景点, 一个景点所包含的信息有:地理位置信息、类别、票价、开放时间()、得分、停留时间等。这些信息表明了景点的得分越高,对用户的吸引力就越大,用户愿意在该景点停留的时间就会越久,愿意为游玩该景点付出的成本就会越高。
定义2旅游路线。旅游路线是由多个旅游景点组成的序列,表示为。其中表示旅游路线中包含的景点,N为景点数目。
定义3路线地图。有向带权图表示旅游区域里的路径信息,是边的集合,是节点的集合。
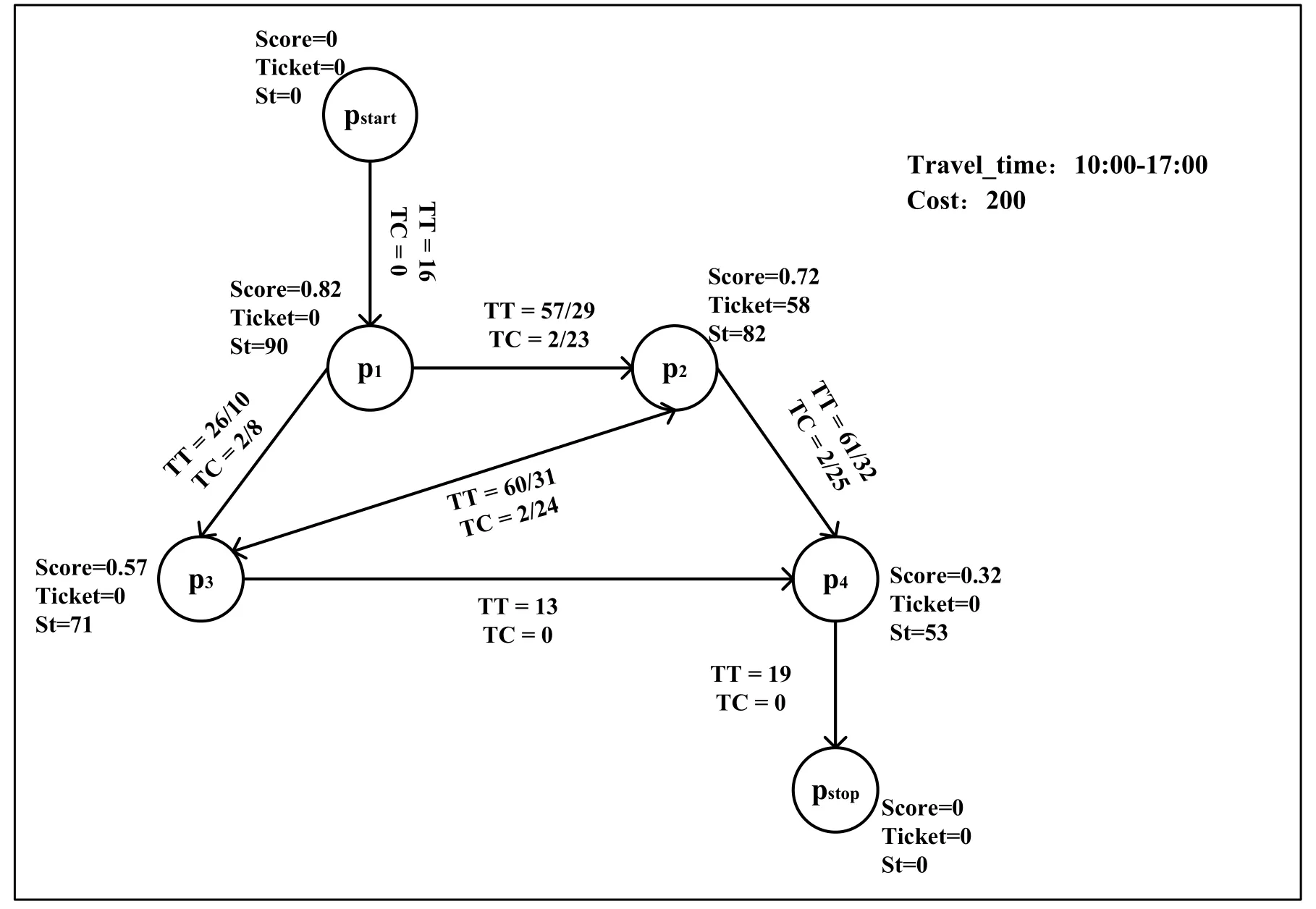
图1:一个旅游路线推荐用户示例
定义4两个景点之间的转移时间。用户从景点到景点所需的转移时间可定义为:

定义5两个景点之间的转移费用。 表示用户从景点 到景点所需的转移费用。在本文中,两个景点之间的转移费用分三种情况,当用户选择步行的情况下,两个景点之间的转移费用为0元,即;当用户选择乘坐公交车,两个景点之间的转移费用为2元,即;当用户选择打士,两个景点之间的转移费用的计算公式如下所示:

其中,我们假设有向的两个景点之间均有一辆公交车可直达,费用为2元;有向的两个景点之间的士均能直达,起步价为。本文所选取的定价均符合成都现行的实际情况。
定义6景点得分。根据用户的历史签到数据感知用户偏好和景点的流行度给出景点的评分方法。景点的得分可定义为:

定义7景点的停留时间。陌生城市对于一个用户而言,在该城市某一景点的停留时间可能会基于自己对于这一景点类别的偏好程度以及该景点的流行程度,但是用户一旦到达了某个景点,不管该景点实际情况如何,都至少会在该景点停留常数T的时间。景点的停留时间可定义为:
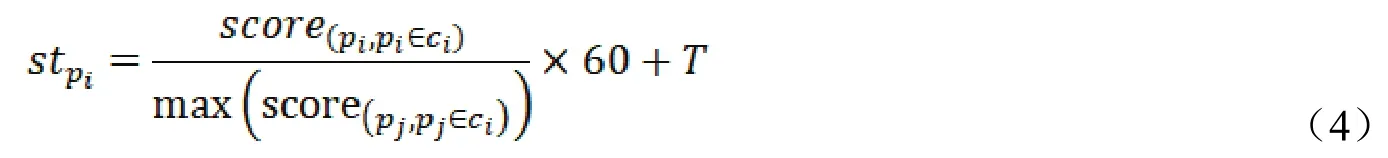
定义 8旅行时间和旅行费用。根据用户给定的起点和终点,对于一段旅游路线,其旅行时间和旅行费用的计算公式如下所示:
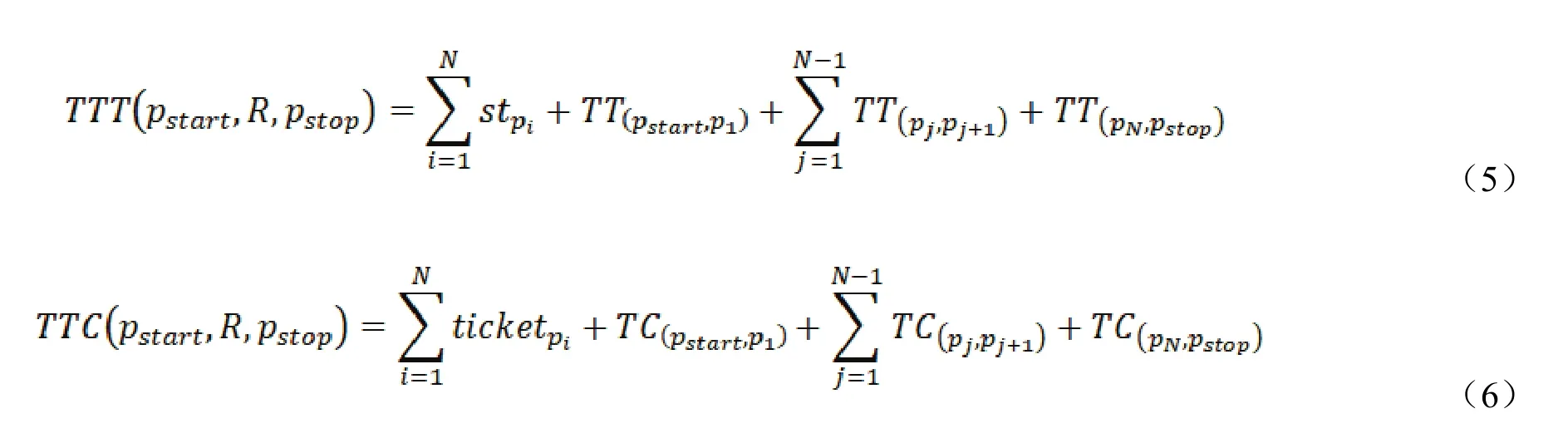
定义9有效行程。假设,和分别表示用户旅程的开始时间、旅程的结束时间以及预算,一段有效的行程必须满足 , 。
三、旅游路线推荐方法
(一)旅游路线推荐框架
如图2所示,本文所提出的旅游路线推荐系统分为两个阶段,第一阶段为离线学习阶段,在该阶段,从旅游网站搜集景点的相关信息,以及根据用户的历史签到数据感知用户偏好和景点流行度;第二阶段为在线推荐阶段,根据用户输入,通过基于多约束多目标的剪枝算法,为用户推荐一条最优旅游路线

图2:旅游路线推荐框架
(二)基于签到数据感知用户偏好和景点流行度的景点评分机制
在进行路线推荐之前,需要了解每个景点对于用户的吸引力。在本文中,景点对于用户的吸引力取决于景点的得分,而景点得分又包含用户偏好和景点流行度两个方面。学习用户偏好,可以感知哪一类景点对用户而言是有吸引力的。一般,人们新到一个城市,并不了解该城市的具体情况,通常都会倾向于逛一些热门景点,本文考虑,某一景点签到的人越多,就说明该景点越流行。故,融合用户偏好和景点流行度对景点进行评分,更符合实际、更具个性化。
1.用户偏好

2.景点的流行度
根据景点的用户历史签到记录,挖掘景点的流行度。景点流行度的计算公式如下所示:
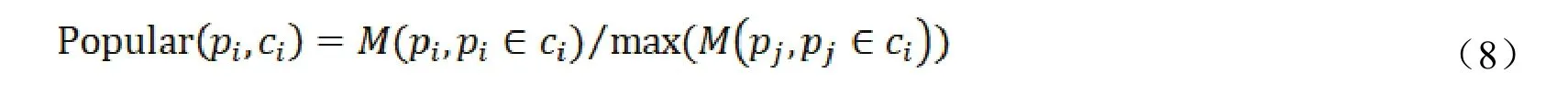
3.基于签到数据感知用户偏好和景点流行度的景点评分机制
在本文中,景点的得分既要考虑用户偏好也要考虑景点流行度,因此,公式(3)对用户偏好和景点流行度进行融合,最终得到景点的得分。
(三)旅游路线推荐算法
1.简单的多约束剪枝算法 MCPA算法
在有向带权图G中,通过遍历满足用户需求的所有可行路径,将景点总得分最高的旅游路线推荐给用户,具体算法描述如下。
算法1 MCPA算法
输出:一条最优旅行路线。
步骤1 根据景点得分,选择Top-K个景点;
步骤3 根据用户输入的预计访问的景点数,生成 条旅游路线;
步骤9 将 路线推荐给用户。
如果只是简单地将景点总得分最高的路线推荐给用户,不考虑景点的多样性,那我们所推荐路线就可能存在多个景点都属于同一类别的现象,这样的推荐结果可能并不是用户想要的。
2.考虑景点多样性的多约束剪枝算法 MCPA-D算法
为进一步接近用户的真实需求,我们提出了MCPA-D算法。
多样性值的计算公式如下所示[15]:
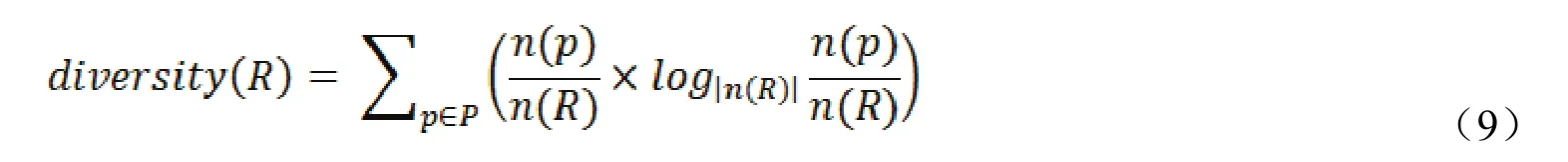
路线得分的计算公式,更新为如下所示:
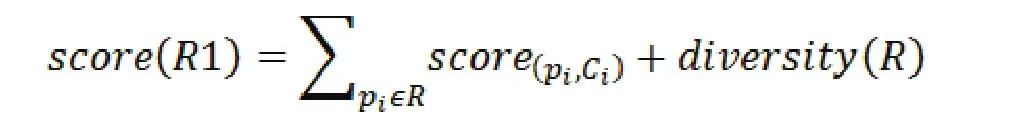
算法2 MCPA-D算法
更新算法1的步骤8-步骤9
步骤9 将 路线推荐给用户。
3.基于多约束多目标的剪枝算法 MCPA-MO算法
一般情况下,人们都希望花尽可能少的时间游览尽可能多的类别不同且得分高的景点,故在满足时间约束和费用约束的前提下,费用低的行程对用户而言会更具吸引力,自然,用户的满意度也会更高,故再考虑旅程的花销得分和时间得分也很有必要。花销得分和时间得分的计算公式如下所示:

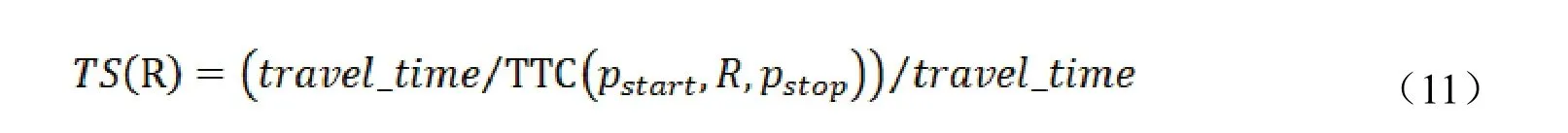
据此,一条旅游路线的最终得分,计算公式如下所示:

算法3 MCPA-MO算法
更新算法1的步骤8-步骤9
(四)路线规划
为了更好的展示本文所提出的算法,我们将以图 1为例进行说明,给定景点的集合,每个景点的信息如表1所示。

表1:景点信息
表2表示由公式(7)计算出的用户偏好得分。表3表示由公式(8)计算出的景点流行度得分;假定,景点得分由公式(3)计算得出,结果如表4所示。
表2:用户的类别偏好
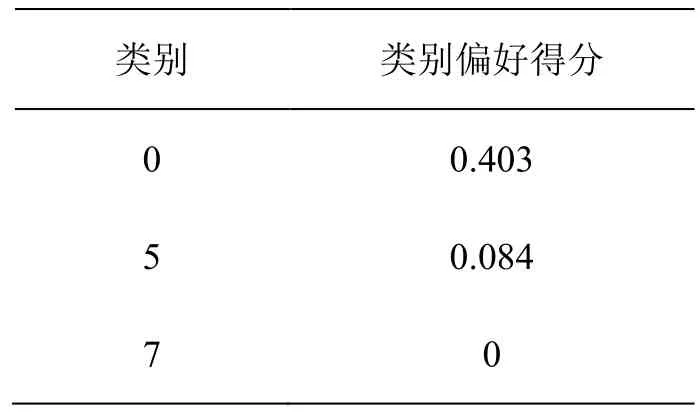
表2:用户的类别偏好
类别 类别偏好得分0 0.403 5 0.084 7 0

表3:景点流行度

表4:景点得分
四、实验结果与分析
(一)实验数据
本文用于实验的数据分为两个部分,一部分来源于Foursquare真实数据集[15],采集的是2009年12月至2013年6月期间在加利福尼亚的签到数据,包括用户ID、兴趣点ID、兴趣点经纬度及其类别信息。数据集中一共含有2551名用户,13474个兴趣点及124933条签到记录;另一部分来源于马蜂窝,获取数据时间截至到2019年2月,获取的数据是成都198个具有不少于10个用户签到的景点数据,包括景点ID、景点位置、景点类别信息、景点开放时间、景点门票以及是否对特殊人群半价(如:学生、老年人)等。另外,通过百度地图,挖掘这些景点的GPS坐标信息。
(二)实验结果与分析
1.MCPA算法与MCPA-D算法推荐效果对比
本文将MCPA算法得到的排名与MCPA-D算法得到的排名相同的top 51条路线进行对比,证明考虑景点多样性的必要性。
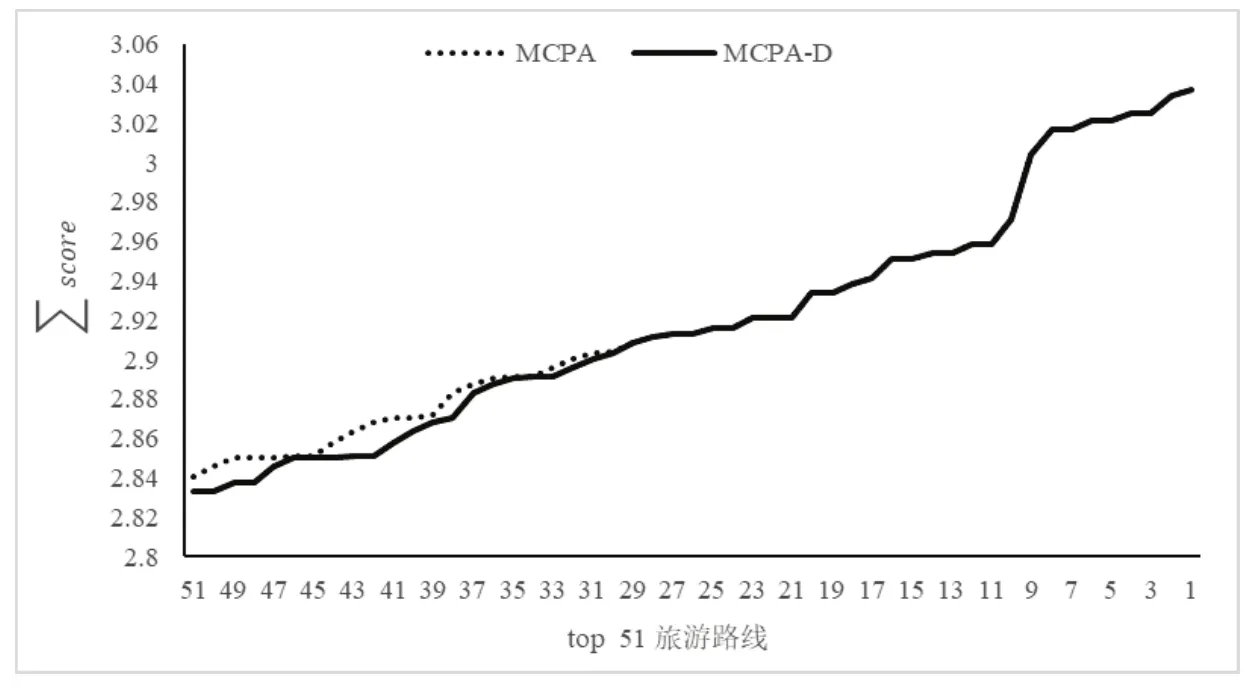
图3:MCPA算法与MCPA-D算法下计算的值
从图3可以看出,两种算法得出top 51条路线的∑score值,其差值范围在[0,0.017], 而MCPA-D算法得出的∑score值居然略小于 MCPA算法下得出的∑score值,此时,我们再将景点的多样性考虑进去,对比两种算法的(∑score + diversity(R))值,结果如图4所示。

图4:MCPA算法与MCPA-D算法下计算的值
从图4可以看出,top 51、top 41、top 39和top 30路线,两种算法得出的值相去甚远,查看数据结果,发现这4条路径,在MCPA算法下,路线中存在类别相同的景点;而在MCPA-D算法下,路线中不存在景点类别相同的景点,路线景点类别情况,如表5所示。
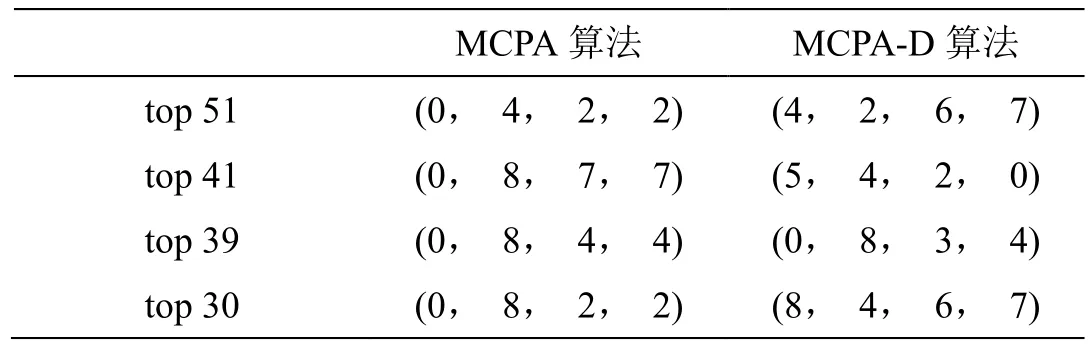
表5:四条路线的景点类别情况
综上,牺牲小部分的∑score值,可获得类别不同的路线。故,考虑景点的多样性是很有必要的。
2.MCPA-D算法与MCPA-MO算法推荐效果对比
本文将MCPA-D算法与MCPA-MO算法分别得到的排名第一的路线进行对比,结果如图5所示,MCPA-D算法与MCPA-MO算法得到的(∑score + diversity(R))值和旅程所花费的时间基本相当,而MCPA-MO算法计算出的花销占比只有2.6%。充分说明考虑花销得分和时间得分的必要性.
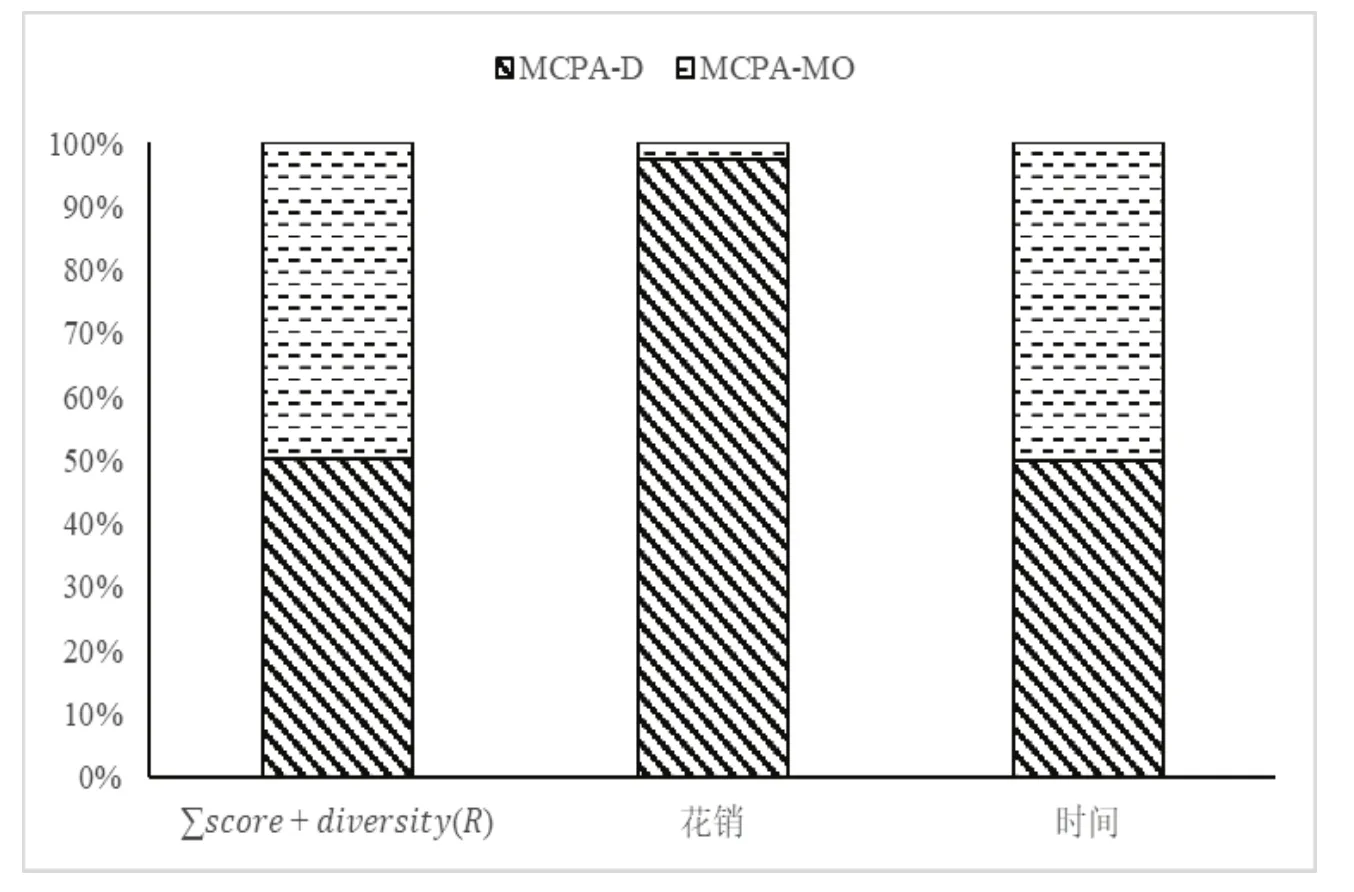
图5:MCPA-D算法与MCPA-MO算法top 1对比
五、结论与展望
本文针对用户希望花尽可能少的钱游览尽可能多的类别不同且得分高的景点这一旅游推荐问题,提出了基于签到数据感知用户偏好和景点流行度的景点评分机制以及基于多约束多目标的剪枝算法。在本文中,我们考虑到了用户偏好、景点流行度以及不同交通工具的选择会对时间和预算约束产生影响,并且使用MCPA-MO算法计算出一条最优旅游路线推荐给用户,以Foursquare社交网站上的真实数据和马蜂窝上成都著名景点的信息作为数据集,实现并评估了推荐算法。实验结果表明,该方法能够为用户推荐更符合现实需求的个性化旅游路线。在未来的工作中,我们将会考虑用户对历史景点的主观评价,通过语义分析对不同推荐结果打正负标签,进一步优化推荐效果。

