高中物理教学中科学建模的策略
俞国富
杭州师范大学附属中学,杭州 310030
《普通高中物理课程标准》指出,物理学科核心素养包括物理观念、科学思维、科学探究以及科学态度与责任。科学思维是物理学科的四大核心素养之一,是从物理学的视角对客观事物的本质属性、内在规律及相互关系的认识方式,是基于经验事实建构理想模型的抽象概括过程[1]。可见,模型建构是科学思维的核心要素,建模能力是科学思维的重要能力指标。模型是根据科学研究需要对研究对象的某些属性进行抽象和简化,从而形成的具有解释和预测功能的近似表征。科学模型是指人们按照科学研究的目的,对研究对象或过程用各种手段与方法(包括物质形式和思维形式)进行再现的产物[2]。物理模型是人们对物理研究对象的过程和结果的一种简化的描述或模拟,是重要的科学模型,也是物理学的重要研究方法。建模就是将实际问题抽象、简化为模型,然后用数学符号或公式、图形、图像或图表加以表征的过程。物理建模就是依据已有经验材料,对一类问题构建问题本质图景,并用物理模型解释和预测现象的科学思维能力的科学实践活动[2]。
1 物理模型的概念
我们在物理教学中,处理物理问题时首先要做的是:①确定研究对象。②分析研究对象在一些理想化的条件下如何运动变化的,其过程遵循什么样的规律。③在观察、实验的基础上,经过物理思维对研究对象提出假说,建立模型。中学物理教材中涉及科学建模的内容很丰富,依据上面几个环节,中学物理常见的模型可分为对象模型、条件模型、过程模型和理论模型[3]。经过仔细梳理,整理了一些典型的实例,并且在此基础上对科学建模能力的培养提出教学建议[4],供各位同行借鉴。
1.1 物理对象模型
物理对象模型即把物理问题的研究对象进行抽象,留取其本质特性而忽略非本质因素建立起来的物理模型。例如,质点、单摆、点电荷、理想电表、理想气体、点光源、薄透镜等都属于对象模型。
1.2 物理条件模型
物理条件模型即把研究对象所处的外部条件理想化,舍去条件中的非本质因素,抽取条件中的本质因素,经过抽象后形成的物理模型。例如,光滑、水平、竖直、轻弹簧、轻绳、轻杆、恒定电流、稳压电源、密闭、真空、绝热等都属于条件模型。
1.3 物理过程模型
物理过程模型即把研究的物理对象的实际运动或变化过程进行近似处理,排除其在实际运动过程中的一些次要因素的干扰,使物理过程由复杂变为简单的、易于理解的理想化典型过程。例如,匀变速直线运动、抛体运动、匀速圆周运动、简谐运动、带电粒子在电场中的类平抛运动、电磁振荡、等温过程、等压过程、绝热变化、准静态过程等都属于过程模型。
1.4 理论模型
理论模型是以实验事实为基础,用已有的科学理论和技术方法为指导,经过物理思维,对未知的自然事物或现象提出假说、作出推测性的解释。理论模型通常是以假说的形式出现,也可称为物理理论假设。例如,光的波动说、光量子假说、光的波粒二象性、氢原子模型等都是理论模型。理论模型具有一定的假定性,只有通过实验验证,才有可能发展为理论。理论模型是一个综合性模型,它自身会包括对象模型、条件模型和过程模型等各种模型的特征性质。
2 物理模型构建的策略
2.1 抽象方式
抽象是一种透过现象深入内部抽取对实际物理现象来说最主要的、本质的特征,忽略其中次要的、非本质的因素的思维过程和方法。在物理建模的过程中,需要通过从现象到本质,不断地提取对事物运动过程或事物之间的相互作用起决定性作用的本质因素,抛弃对事物运动过程或事物之间的相互作用无关紧要的非本质因素,从复杂多变的运动过程和相互作用过程中提取事物的共性,进而建立物理模型。抽象方式是物理建模常用的基本的思维方法,高中物理教材中许多模型都是通过抽象的方式建立起来的。因此,在教学中我们要引导学生从物理事实出发,注重抽象方式建立物理模型[5]。表1是中学物理教材中采用抽象方式建模的一些典型实例。

表1 抽象方式建立物理模型
2.2 理想简化
理想简化是针对错综复杂的实际物理问题,在不改变问题的规定性、不降低问题的探索性的前提下,抓住影响问题的本质因素,忽略问题的非本质因素,将物理问题进行简单化、理想化处理。用理想简化方法构建的物理模型是在理想状态下才有的,在现实物理问题中却是不存在的。用理想简化方法构建的物理模型能排除非本质特性、次要因素的干扰,从而使实际物理问题由复杂变为简单的、易于处理的理想化物理模型。表2是中学物理教材中采用理想简化方法建模的一些典型实例。
2.3 类比联想
所谓类比就是根据两种事物在一些属性上的相似性,通过比较和联想,推理出它们在另一些属性上可能也相似的思维形式 。类比联想包括两方面的含义:(1)联想,即由新信息引起的对已有知识的回忆;(2)类比,在新、旧信息间找相似和相异的地方,即异中求同或同中求异。类比的方法在物理学的研究过程中起着至关重要的作用,许多物理模型的建立都运用了类比联想。开普勒曾经说:“我珍视类比胜于任何别的东西,它是我最可信赖的老师,它能提示自然界的秘密”。英国的培根有一句名言:“类比联想支配发明”。应用类比联想可以在两个不同知识领域之间进行知识迁移,而且这也是科学的新思想和新发明产生和形成的一种重要思维方法,特别是在还不足以进行归纳推理和演绎思维的情况下,类比更是得天独厚。表3是中学物理教材中采用类比联想建模的一些典型实例。
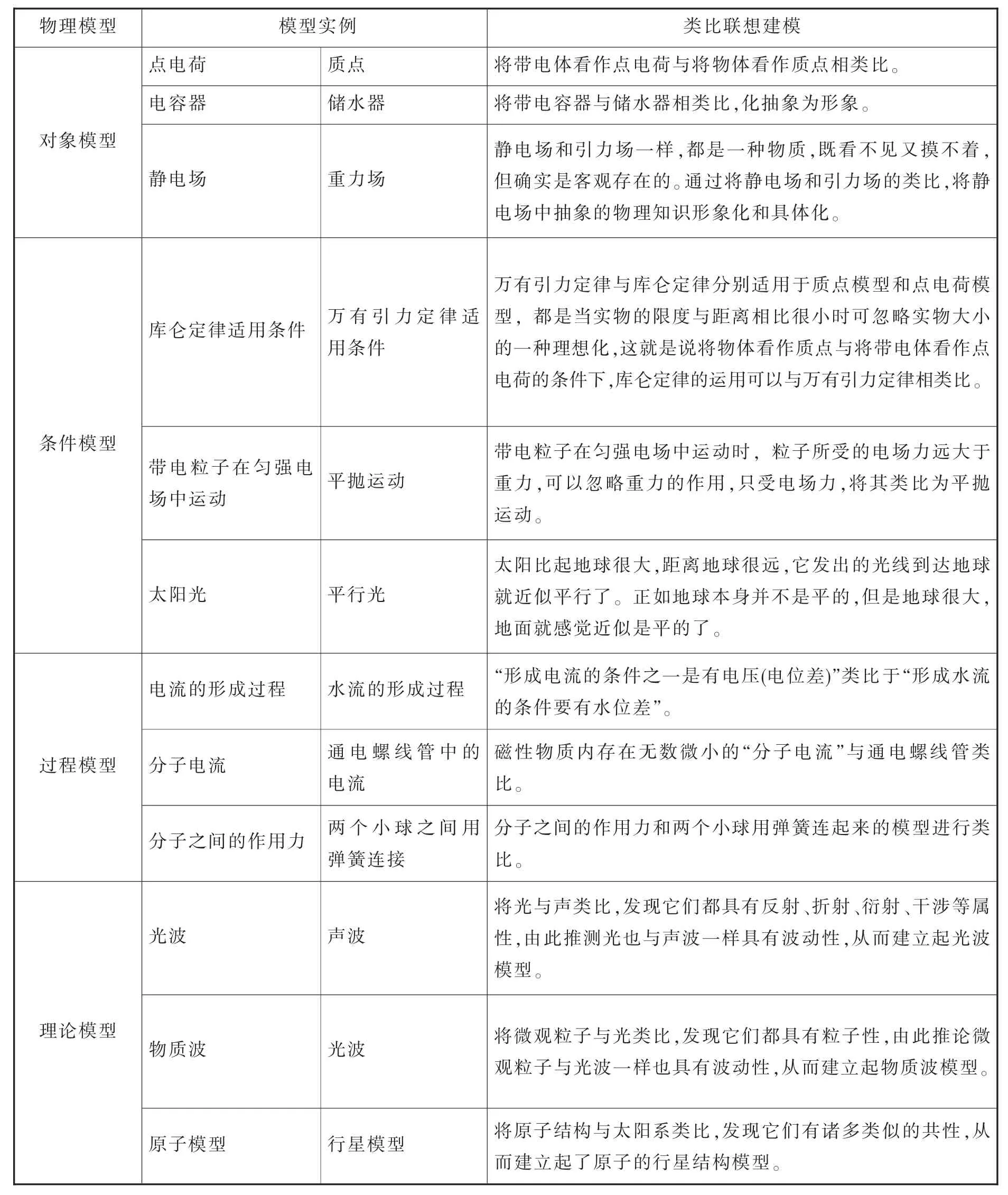
表3 类比联想建立物理模型
应用类比联想进行物理模型构建也并非万能的,有时还可能造成错误的结论。因此,运用类比联想建立物理模型其正确性与科学性还必须接受实践的检验。
2.4 等效替代
等效替代法指当一个研究对象在某一方面的作用效果与另一个研究对象的作用效果相同、或两个研究对象的物理过程在某一方面有共同结果时,就可以在相互之间进行替代的建模方法。等效替代把较复杂的物理现象和物理过程转化为等效的、简单的物理现象和过程,从而能够更方便地解决问题。运用等效方法得到的物理模型就是等效模型。表4是中学物理教材中采用等效替代建模的一些典型实例。

表4 等效替代建立物理模型
如果物理过程比较隐蔽、复杂、难以直接研究,可以采用等效替代法建立起相应的比较直观、简单、易于直接研究的等效物理模型。如图1,研究LC振荡电路时用单摆振动模型去等效类比电磁振荡过程;LC振荡电路一周内充放电过程中的电流、电容器极板间的电压、场强、电场能以及线圈中的磁场、磁场能等物理量的变化可以用我们熟悉的单摆一周内的运动过程中相应的物理量来比较分析。我们发现,单摆和LC振荡电路,尽管它们的结构相异,但它们的动态特性随时间的变化规律却完全相同,因此可以建立起相应的替代模型。

图1 等效物理模型

图2 弹簧和小圆环
再比如,我们在物理教学中碰到这样的例子:如图2所示,将长度为L的光滑钢丝绕成高度为h的弹簧,弹簧竖直固定在地面上。现将一个小圆环穿在钢丝上并从最高点由静止释放,求小圆环沿弹簧滑到最低点的时间。显然该问题的物理过程比较隐蔽、复杂,此时我们要化隐蔽为直观、化复杂为简单,运用等效替代法建立物理模型。把螺旋线运动等效为斜面上的直线运动,可以把小球看作物体在长为L、高为h的光滑斜面上由静止下滑的过程,根据牛顿第二定律即可迎刃而解。等效替代作为一种重要的思维方法,在解决难题时可以起到化难为易、化繁为简的作用。
2.5 假设验证
假说是物理建模的一种重要方法,正如恩格斯所说:“只要自然科学在思维着,它的发展形式就是假说。”运用假说的方法建模是指在物理现象真相还不清楚,为了从根本上揭示事物现象的本质,依据已有的理论事实,建立一个新的物理模型的方法。这个模型能说明已有的实验事实,并能预测可能出现的结果。假说是对物质本质的不完全归纳,因此,采用假说方法所建立的模型,需要经过实验的验证,并需要根据条件的变化进行补充和完善[3]。例如,对于原子核模型的建立,每一次重大的发展都是根据一定的事实提出相应的原子核模型(假说结构),再去利用新的实验或事实验证其正确性[6]。表5是中学物理教材中采用假设验证建模的一些典型实例。
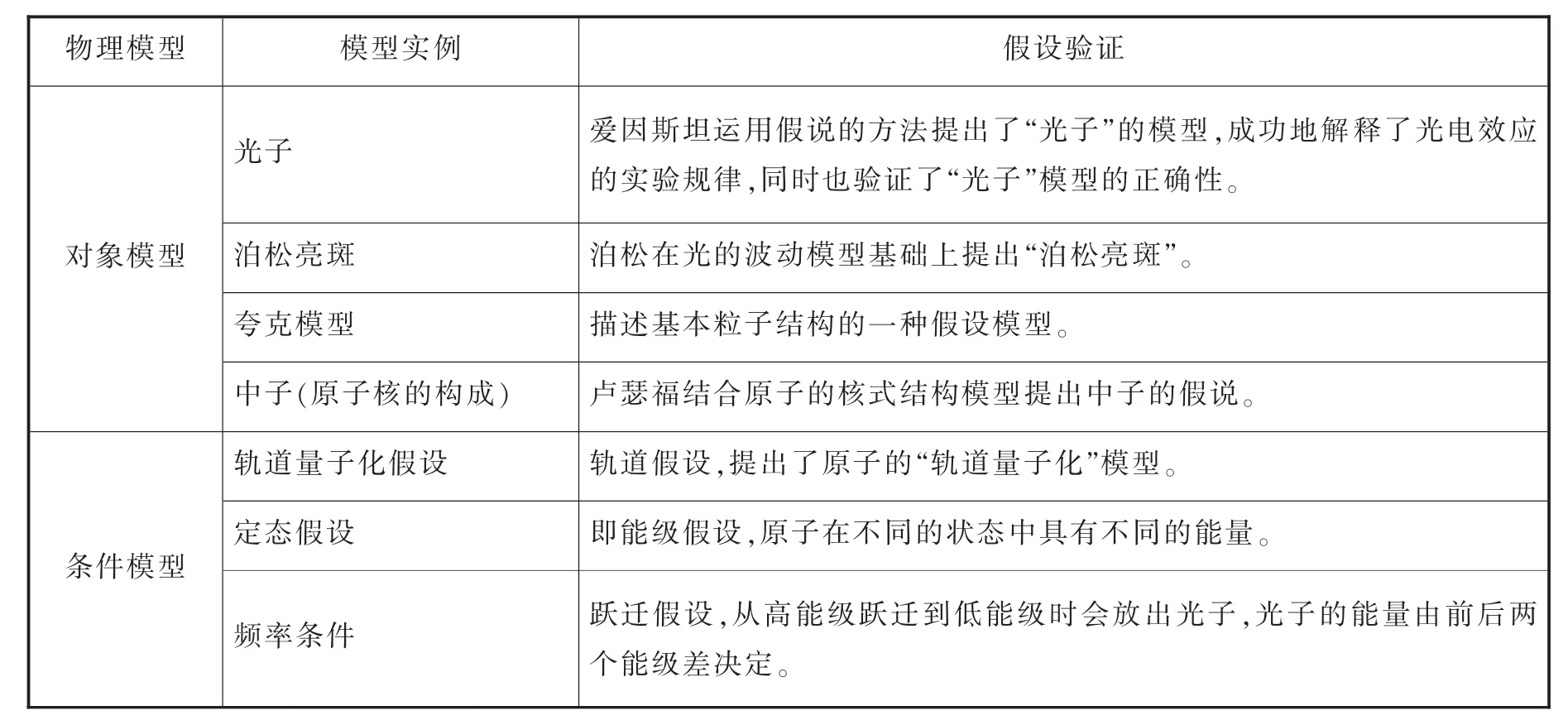
表5 假设验证建立物理模型

续表5
根据模型和建模的定义,高中物理教学中主要有对象模型、条件模型、过程模型和理论模型四种。在我们的研究中提出了抽象方式、理想简化、类比联想、等效替代、假设验证都是物理教学中建模的有效方法。高中物理教材中蕴含着丰富的建模内容,教师在教学中应该充分利用教材中有关建模的素材,加强对学生科学建模能力的培养,从而提升学生的思维品质与学科素养。针对每种具体方法,对四种模型的建构过程所做出的模型实例可为高中物理教学提供借鉴。

