找寻零点的策略探究

江苏省无锡市洛社高级中学 徐荣新

在函数的解答题中常遇到零点个数的问题，由于题型的要求，我们需要严谨解答，而不是模棱两可或者简单的“由图可知”，那么到底应该如何作答？本文旨在认识到可能的错误性基础上尝试给出理论依据和常见的策略。

x （0，10） 10 （10，+∞）f'(x) - 0 +f(x) 递减 极小值 递增

所以f(x)的最小值为f(10)=ln10-3 ＜0，

故函数f(x)在区间（1,10）和（10，e+）之间各有一个零点，又由单调性可知函数f(x)有且仅有两个零点。

注解：此题为了说明存在两个零点，并没有直接由单调性得到，而是在单调性的基础上利用零点存在性定理，找到了函数值为正和为负的点，进行了严谨的代数说明。

基于上面这个例题的剖析，我们意识到在解答题中确定零点问题不能想当然，唯一合理的依据是零点存在性定理，即“一般地，如果函数y=f(x)在区间[a，b]上的图像是连续不断的一条曲线，并且有f(a)f(b)＜0，那么函数y=f(x)在区间(a,b)内有零点”。但问题的关键也在于如何找寻函数值为正或为负的点，下面我们就来归纳找寻正负函数值，从而确定零点的方法。

例1：设函数f(x)=lnx-ax，其中a为实数。试判断函数f(x)零点的个数，并证明你的结论。

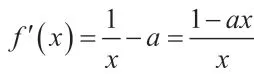
（1）当a=0 时，函数f(x)=lnx，显然存在一个零点。

（2）当a＜0 时，f'(x)＞0，函数f(x)在（0，+∞）上单调递增，

显然f(1)=-a＞0。（此处取值采用了针对lnx的特殊值）

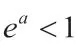
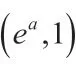
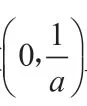
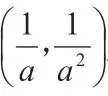
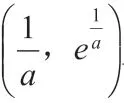
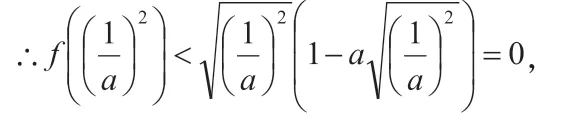
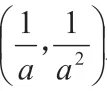
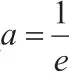
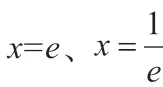
已知函数m（x）=x2，函数n（x）=a+1（a∈R）。

（1）若a=2，求曲线y=n（x）在点（1，n（1））处的切线方程；

（2）若函数f（x）=m（x）-n（x）有且只有一个零点，求实数a的取值范围。

问题（1）略；问题（2）的答案为a≤0 或a=2。