冥族小天体与海王星特洛伊的近密交会

董城昱，周礼勇

(1.南京大学 天文与空间科学学院，南京 210046；2.南京大学 现代天文与天体物理教育部重点实验室，南京 210046)

1 引 言

海王星特洛伊(Trojan,TR)小天体是与海王星同享日心轨道的一群小天体。与太阳系中的其他特洛伊天体类似，海王星特洛伊处在海王星的拉格朗日稳定区域，即在太阳-海王星系统中处于海王星轨道前方(或后方)约60◦的L4 (或L5)点。特洛伊天体群、海王星和太阳大致构成一个等边三角形。海王星特洛伊与海王星有大致相同的轨道半长径和轨道周期，并且它们之间的平经度之差始终在一个范围内秤动，因此，我们也称海王星特洛伊与海王星间存在1:1 的平运动轨道共振。截至2018年11月，人们已发现22 个海王星特洛伊，其中有19 个处在L4 点，3 个处在L5 点[1]。

在海王星轨道之外还存在着为数众多的海王星外天体(trans-Neptunian object,TNO)，包括柯伊伯带天体(Kuiper belt object,KBO)、散射盘天体(scattered disk object,SDO)和内奥尔特云天体等。一直以来人们通过对它们进行研究来揭示早期太阳系的状态和演化过程。TNO 中有一群小天体与海王星保持着2 :3 的平运动轨道共振，其轨道半长径约为39 AU。由于其轨道性质与冥王星类似，因此它们被称为冥族小天体(plutino,PL)。冥族小天体是共振柯伊伯带天体(resonant KBO)中最大的一类，除了最大的冥王星以外，它还包括亡神星(Orcus)和伊克西翁(Ixion)等。

冥族小天体的轨道偏心率可达0.3，这意味着它们经常穿越海王星的轨道，并与海王星特洛伊群发生交会。Almeida 等人[2]认为，这两群小天体之间可能存在的碰撞会对两群小天体的表面颜色产生重要影响。同时，他们还认为，冥族小天体引起的近密交会(close encounter,CE)或碰撞可能使得低轨道倾角处的海王星特洛伊减少或碎裂，因此，海王星特洛伊的尺寸普遍较小，且在高轨道倾角上分布较多。据估算，海王星特洛伊在高倾角轨道处的数目远远超过低倾角轨道处的数目[3]，而这一轨道分布特征不是当前太阳系构型的动力学演化结果[4,5]，也不是目前被广为认可的行星迁移过程的结果[6]，因此，该现象一直令天文学家感到困惑。Almeida 等人[2]通过简单的数值模拟来验证冥族小天体与海王星特洛伊之间的相互作用。他们对一些实际的冥族小天体和海王星特洛伊的轨道积分至109a，并以105a为时间间隔检查这些轨道在海王星轨道面上的投影，发现两者之间存在大量的重叠。当冥族小天体轨道偏心率较大、轨道倾角较低、共振振幅较大时，两群天体之间的轨道重叠就较大。通过数值方法，Almeida 等人[2]还对冥族小天体与海王星特洛伊之间的近密交会和碰撞的次数进行了估算。尽管在模拟中很少直接检测到交会或碰撞，他们仍然认为在实际情况下交会和碰撞是十分频繁的，并且其频率应比两群小天体自身内部的交会频率要高。

因为冥族小天体和海王星特洛伊分别被与海王星的2 :3 和1 :1 平运动共振所束缚，Almeida 等人[2]所描述的近密交会甚至碰撞确实很可能在整个太阳系年龄内持续发生，且其动力学效果有可能在长时间内累积，从而对两群小天体产生重要影响，甚至决定它们当前的轨道分布特征。然而，在小天体所处的广阔空间内，个别小天体之间的近密交会或碰撞仍然是极为罕见的事件，一般的数值模拟受制于计算能力，即使参与模拟的小天体数目非常大，仍然难以探测到足够多的交会或碰撞事件。Almeida 等人[2]仅仅作了较粗糙的数值模拟，对近密交会或碰撞的效果也并未进行具体分析，因此，未能彻底解决这一问题。在本文中我们将使用更严格的数值模拟与计算，精确地检测海王星特洛伊与冥族小天体之间的近密交会。在控制变量的前提下，我们通过改变两群小天体的物理和轨道性质，探究了影响两群小天体之间近密交会的关键因素。在数值模拟结果的基础上，我们建立了半解析方法，推算出了两群小天体之间碰撞的频率，从而解决了因为碰撞尺度过小而难以进行数值检测的问题。此外，在冥族小天体现有观测数据的基础上，本文对其质量分布进行了估算，并将之应用于实际情况下两群小天体之间近密交会和碰撞次数的推算。

本文第2 章介绍我们所采用的模型和数值模拟方法；第3 章展示由数值模拟结果得到的近密交会次数与轨道根数之间的关系；第4 和第5 章建立分析方法，以计算两群小天体之间近密交会和碰撞的次数；第6 章对实际情况进行分析；第7 章进行总结和讨论。

2 模型和数值模拟方法

为了计算效率和控制变量的需要，我们在数值积分中每次只包括一个PL 和一个TR。4 个小天体被选作典型例子，它们的轨道根数信息见表1。每次只改变PL 或TR 的某一个轨道根数，然后大量取样并作相应数值积分，来显示不同的轨道根数如何影响近密交会。

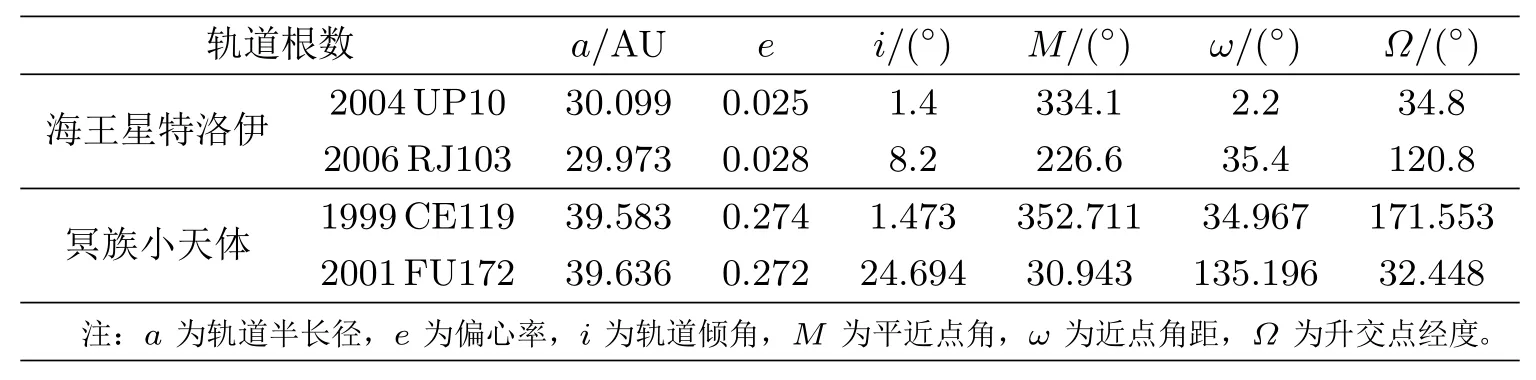
表1 几个典型海王星特洛伊和冥族小天体的轨道根数(JD 2454200.50)[1]

我们在模型中忽略了其他大行星的作用，只包括太阳、海王星和两群发生近密交会的小天体PL 和TR。实际上，木星、土星和天王星对这两群小天体的近密交会几乎不会产生直接影响，而来自这些行星的间接作用或由它们引起的长期效应仅引起小天体轨道细微而缓慢的变化，并不足以影响两群小天体因交会或碰撞所导致的在统计意义上的演化过程[7]。鉴于PL 的质量与海王星相比非常小，该模型基本上是一个在第四体(PL)摄动下的限制性三体(太阳、海王星和TR)问题模型。

我们用SyMBA 数值积分包[8]来处理以上问题。为了能够合理地处理CE 过程，并捕捉必要的信息，我们对相关程序做了一些必要的修改。我们把用于判断两个小天体是否发生CE 的距离阈值设定为两个小天体中相对较大的那一个(一般情况下是PL)的希尔半径(Hill radius)的3.5 倍。在每一个积分步长中，我们都会计算当前TR 的速度矢量。如果这个矢量指向以PL 为中心，以距离阈值为半径的球面范围，并且TR 与PL 的距离在数个步长之内，我们就开始减小积分步长。两者距离越近，步长会缩得越小，这样就可避免因为积分步长太大而错过部分近密交会的情况。通过上述策略，一般情况下积分步长可以设得稍大一些。我们设积分步长为0.1 a，这样，交会小天体在一个积分步长内穿过的距离约为0.1 AU。所有的模拟都积分至109a，即太阳系年龄的时间尺度。

3 数值结果

3.1 CE次数与PL质量的关系

我们首先使用数值模拟方法来研究CE 次数与PL 质量的关系。PL 的质量显然是影响CE 次数的决定性因素。我们以1999 CE119 和2004 UP10 这一对小天体为例，在所有初始轨道根数保持不变的情况下，将PL 质量在10−3～1 倍冥王星质量内取若干值，再对每一个值进行数值积分，并记录CE 发生的次数，结果如图1所示。

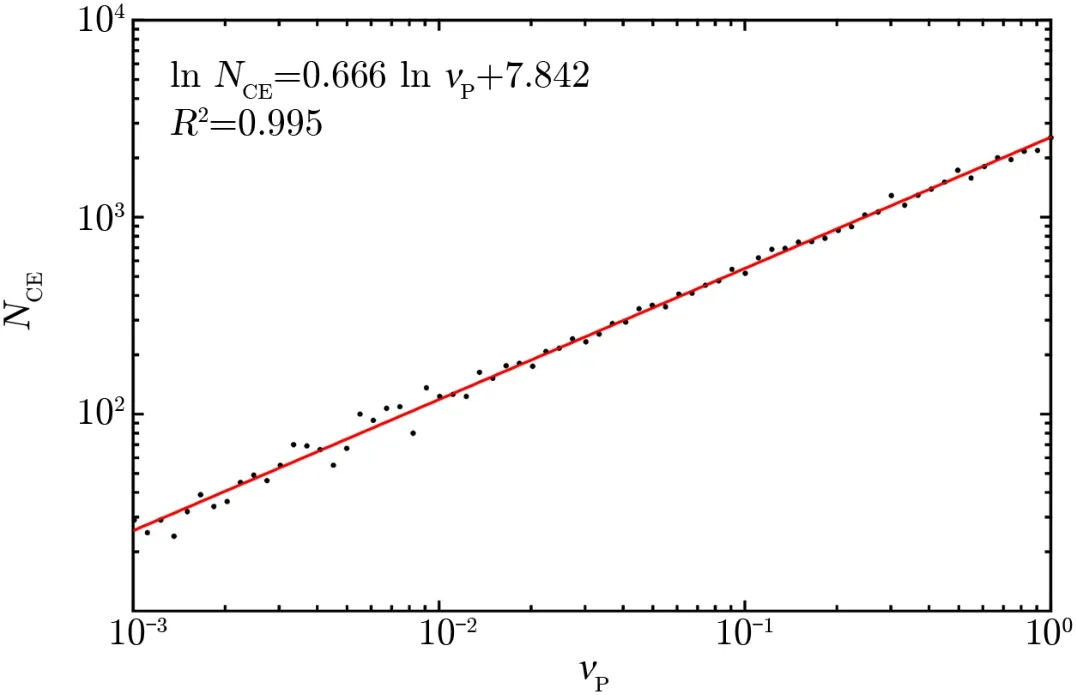
图1 CE 次数与PL 质量的关系

由图1可以看到，在双对数图上CE 次数NCE与νP成线性关系(νP=mP/mPluto，mP为PL 的质量，mPluto为冥王星的质量)，这意味着它们之间存在简单的幂律关系。通过线性拟合我们可以得到幂律的近似值：

3.2 CE次数与轨道倾角的关系

小天体的轨道倾角决定了两个小天体轨道面的距离，它会影响小天体之间的交会或碰撞概率。我们随机选定TR 2004 UP10，并在模拟数据中测量具有不同轨道倾角的PL 与它的CE 次数。保持其他轨道根数不变，只对1999 CE119 和2001 FU172 这两个PL 的初始轨道倾角在0◦～30◦之间取值，并模拟它们的轨道演化，统计PL 与TR 之间CE 的数据。数值模拟中，小天体PL 质量仍然采用冥王星质量。

模拟的结果如图2a)所示。由图可见，当PL 的轨道倾角IP增加时，CE 次数逐渐减少。但当IP很小的时候，其趋势则相反。峰值出现在PL 的轨道倾角与TR 的轨道倾角相同时。也就是说，当两者的轨道倾角接近时，CE 的概率最大，这是因为此时PL 与TR 的轨道面有最大机会相互接近。我们还可以看到，PL 轨道倾角变化引起的CE 次数发生的变化基本上在1 个量级以内，与PL 质量变化对其产生的影响相比其影响较小。

TR 的轨道倾角IT也会影响CE 次数，倾角越大，TR 与PL 交会的概率就越小。一般而言，只有相对轨道倾角才有实际的物理意义。在我们考虑的模型中，海王星的轨道面是基本固定的，而TR 和PL 相对于海王星轨道面的倾角都会影响它们轨道的特征，所以有必要单独讨论TR 轨道倾角对这两群小天体之间的近密交会的影响。以1999 CE119 这个PL 和两个TR (2004 UP10 和2006 RJ103)为例，保持TR 的其他轨道根数不变，仅改变它们的初始轨道倾角，来分析CE 的情况。最后结果如图2b)所示。由图2b)可以看出，TR 轨道倾角的变化对CE 次数的影响也基本在1 个量级以内，并且与图2a)一样，当两者轨道倾角相近时，CE 的次数达到最大值。

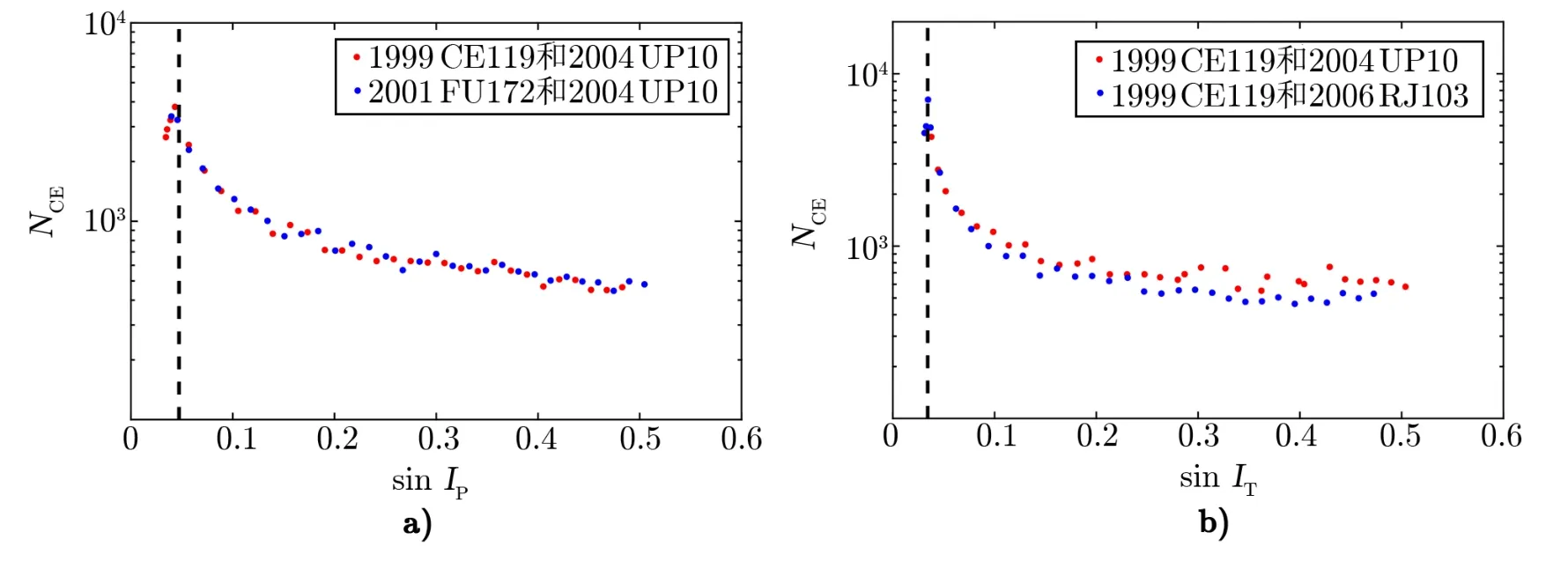
图2 CE 次数与轨道倾角的关系

3.3 CE次数与PL轨道偏心率的关系

轨道偏心率决定了轨道向内外延展的程度，决定了两群小天体轨道交叉重叠的程度，因而也会影响两群小天体的交会概率。因为只有低偏心率的TR 轨道才是稳定的[5]，所以在讨论PL 和TR 偏心率对两者之间CE 次数的影响时，只需要讨论PL 的轨道偏心率即可。仍旧以上述两对小天体为例，仅改变PL 的偏心率eP，保持所有其他轨道根数不变，计算CE次数。计算结果如图3所示。

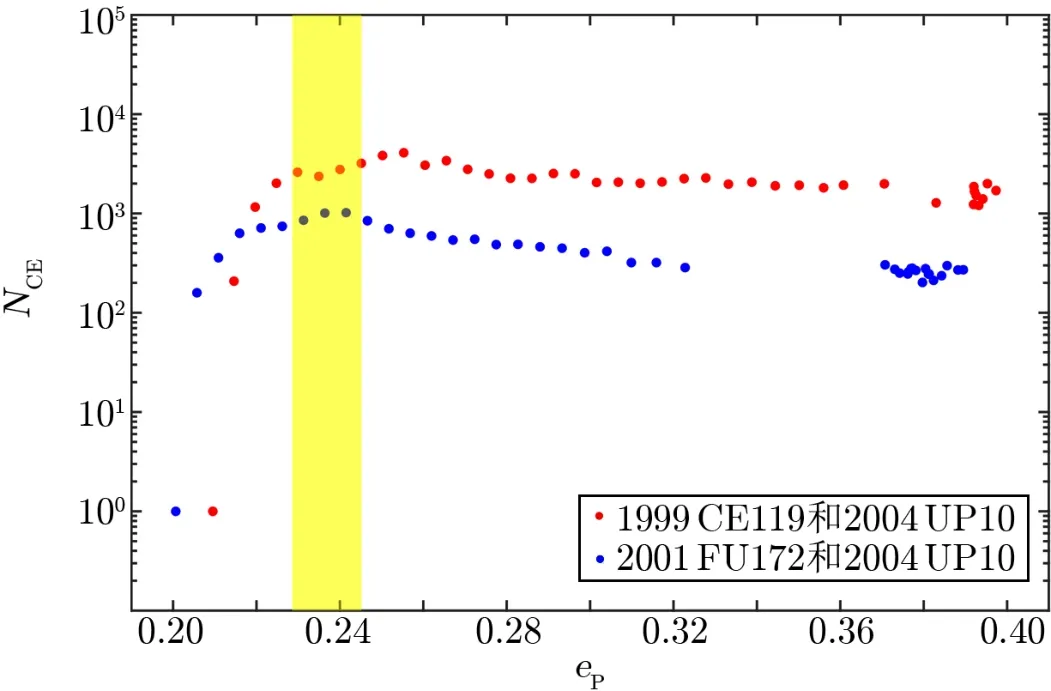
图3 CE 次数与PL 轨道偏心率的关系

由图3可以看出，随着eP的增加，CE 次数先增加，然后又缓慢减少，并在黄色区域附近达到最大值。黄色区域表示的是当PL 的近日点处在TR 近日点与远日点之间时，PL偏心率的范围eE～eX，显然这种情况下发生CE 的概率最大。当eP持续增大，PL 的近日点深入到TR 轨道内部时，因为两个小天体轨道交叉的部分并没有增加，所以CE 次数的变化不明显。当PL 近日点在TR 远日点之外时，理论上这两个轨道应该不会交叉，但实际上仍有一些CE 发生。这是因为我们在统计中采用的是以一定时间间隔记录的轨道根数平均值，以去除瞬时变化的影响，但在实际模拟中这些轨道根数会有起伏。

3.4 CE次数与共振振幅的关系

平运动共振的振幅反映了天体在共振中秤动的情况。Almeida 等人[2]认为，PL 与TR的共振振幅∆ϕ对近密交会有重要作用，并且共振振幅越大，CE 的概率就越高。然而，在我们的模拟结果中，共振振幅对CE 的影响并不大。一般来说，共振振幅越大，两条轨道重叠的面积也越大。但实际上并不是重叠区域的面积，而是在重叠区域内星子出现的频率直接决定了CE 的概率。如果我们像Almeida 等人那样处理，每隔一段时间记录PL 的位置，并将其投影到TR 轨道平面上，那么，因为总时间是固定的，总的投影点的数量也必然是固定的。由于增大重叠面积的同时会降低点的密度，而这里的密度实际上代表的就是PL 在某一区域出现的频率，因此，即使轨道重叠面积因共振振幅的增加而增加，CE 概率也不一定会增加。

我们可以通过随机改变PL 的Ω,ω和M的初始值，从而改变PL 的振幅来进行验证。我们把经过演化后能够稳定存在于共振区内的PL 所在的模拟结果挑选出来，即可得到CE的次数与PL 的共振振幅的关系。TR 的共振振幅对CE 的影响也可以通过类似方法进行验证。我们将结果一并总结在图4中。

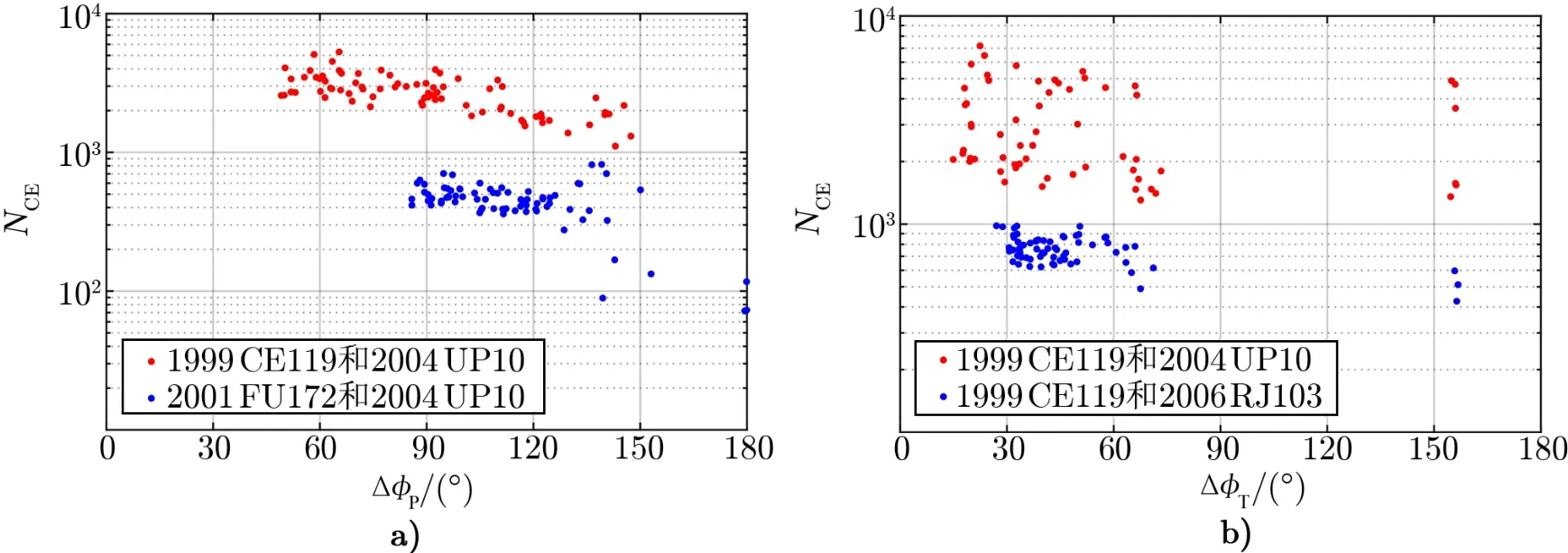
图4 CE 次数与小天体共振振幅的关系

图4a)中，每个模拟中PL 的共振振幅∆ϕP是不同的。数值模拟中初始的ΩP,ωP和MP随机产生，其他根数保持不变。图4a)中显示的共振振幅是演化中的平均值，其中振幅接近180◦的几个点所代表的轨道稳定性较差。图4b)中，每个模拟中TR 的共振振幅∆ϕT是不同的，共振振幅小于80◦和大于150◦的两群小天体分别对应TR 的蝌蚪形和马蹄形轨道。可以清楚地看到，随着共振振幅的变化，CE 的次数并没有明显增加，甚至还有一定程度的减少。

4 CE次数的理论计算

计算两群小天体之间CE 的次数问题与计算CE 的概率问题类似，许多前人对后者进行过探索[9,10]。本文将对CE 次数做一些理论分析，以便在数值结果的基础上通过半解析的方法计算实际情况下的CE 次数。

4.1 CE次数与质量的关系

小天体之间的相互引力会使两者的轨道发生偏折，但本文讨论的交会和碰撞次数是两个小天体之间的距离小于给定阈值之后的必然结果，而进入阈值距离之前小天体间的引力作用可以忽略，其引起的轨道偏折自然也可忽略。如果仅希望从统计意义上对交会或碰撞进行半解析的研究，为简单计，可以直接从经典的碰撞截面角度来看这个问题，以避免引入复杂的修正系数来详细刻画轨道偏折。我们也将看到，这一简化所得到的结果与数值模拟的结果一致。

当碰撞完全随机时，在某个半径R内CE 发生的概率P应与其碰撞截面成正比，即：

这里假设在半径RU内碰撞的概率为1。显然RU表征的是两个轨道在空间可能碰撞的区域的尺度，它应与小天体的日心轨道特征有关。既然小天体质量比太阳质量小很多，两个小天体的质量都并不足以对其轨道性质产生本质的影响，所以RU应与小天体的质量基本无关。假设在RU内发生CE 的总次数是NU，那么两个小天体发生CE 的总次数为：

其中，Rth为第2 章中设定的CE 阈值半径(相对较大的小天体的希尔半径的3.5 倍)。

假设两个小天体演化的总时长是ttot，而PL 的轨道周期是torb。由于它们分别处在2:3 和1:1 共振中，每隔两个周期PL 就会遇见TR，也就是说，PL 和TR 的轨道状态的总周期是2 个PL 轨道周期。这样，在ttot时间内最多可能发生的CE 的次数NU为：

其中，aP是PL 的半长径，ttot以年为单位，aP以天文单位为单位。

把CE 的阈值半径设为PL 希尔半径的倍数，显然是因为它与PL 的质量有关。由希尔半径的公式，我们可以得到：

其中，M⊙是太阳的质量，κth是CE 的阈值半径与希尔半径之比。此处我们使用了简化的圆轨道希尔半径。最后，我们可以将CE 次数写成PL 质量的函数：

其中，

在这里，我们把PL 的质量mP用冥王星质量做了无量纲化处理。

容易看到，CE 次数与PL 的质量成幂次关系，其幂律(2/3)与图1得到的拟合结果(0.665 8)基本一致。式(7)中参数Ru表征各种轨道特征对CE 的影响，例如前面所讨论的PL 和TR 的轨道倾角、偏心率和共振振幅等。这些轨道特征决定了PL 与TR 轨道在空间上交叉的概率。由各轨道根数直接推算参数Ru是比较复杂的，并且第3.2―3.4 节的数值结果已经表明，轨道根数对CE 次数的影响较小，我们在此不对Ru做细致的理论计算，而是从数值模拟的结果中推算Ru。所以有必要在此强调，以下估算CE 次数的公式实际上是半解析的。

4.2 一群PL的CE次数

如第4.1 节所述，CE 次数可写成PL 质量的函数。该表达式也可以推广到多个PL 的情形，适用于实际情况。

4.2.1 简单情形

首先讨论最简单的情形，即所有的PL 质量和轨道都是完全一样的情形。这种情况下的CE 总次数容易得到。假设PL 总质量是而PL 总个数为那么单个PL 的质量为根据式(6)，总CE 次数应为：

式(10)表明，在总质量给定的情况下，单个PL 的质量越小，PL 的总数越多，CE 次数就会越多。因为我们在判定CE 的时候考虑的是希尔半径，所以小质量的PL 也会在CE 中影响TR 的轨道。然而，即使都在希尔半径内，小质量的PL 与大质量的PL 造成的影响显然不一样，所以更多的小质量PL 导致更多的CE，并不一定意味着总的影响效果也会变大。

4.2.2 给定质量分布

一般来说，一群PL 遵从一个质量分布。既然质量是CE 次数的决定性因素，而轨道特征至多带来量级之内的影响，因此，我们仍然简单地假设所有的PL 都有完全相同的轨道性质，这样我们就可以继续使用式(6)。

且其总质量符合下式：

其中，νP,b是PL 质量的下界，而积分的上界始终是1。也就是说，我们始终以最大质量的那个PL 作为参考。当然，实际情况下，那个PL 就是冥王星。

这样，质量在(νP,νP+dνP)区间内的PL 个数是：

假设此质量区间内PL 的质量都为区间的下界，那么这个质量区间内PL 贡献的CE 次数是：

所以总的CE 次数是：

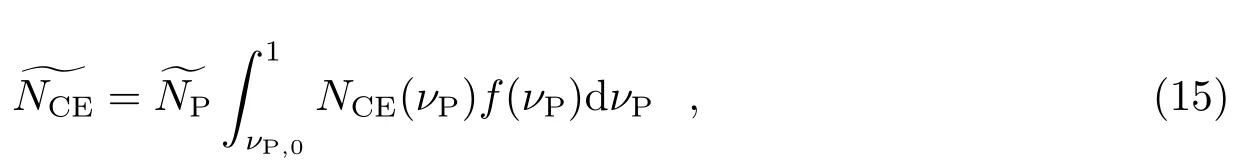
其中，νP,0是积分下界。既然我们讨论CE 次数，一个必须满足的条件是PL 和TR 之间的距离不能太近。如果PL 的CE 阈值半径小于TR 的物理半径，那么这个时候应该发生了碰撞，而不是近密交会。假设TR 的物理半径是RT，那么应该有：

根据式(5)可以得到：

这个下界是由物理条件所限，我们称之为硬下界。

另一种情况下，我们考虑PL 的CE 阈值半径不比TR 的CE 阈值半径小，否则我们在计算CE 次数时首先考虑TR 对PL 的影响，而这很可能会改变PL 的轨道性质。因此，我们有：

其中νT=mT/mPluto，mT为TR 的质量。我们称这个下界为软下界。

最后，再考虑式(15)的近似问题。我们是从最简单的碰撞截面角度推导出式(6)，进而得到式(15)的。对CE 次数的理论计算必然要比实际情况少一些，因为在单纯的碰撞截面中我们没有考虑两个小天体之间的引力，而引力的聚焦修正通常会使两个星子之间的距离更近。

另一方面，既然我们近似地认为所有PL 的轨道性质都相同，而实际应用的时候我们又经常取CE 条件最好的轨道作为例子(根据第3 章的数值模拟结果，就是轨道倾角较低，轨道偏心率适中的情形)，这样，总的CE 次数会被高估。

综合考虑上述两种情况，我们相信，由式(15)给出的总CE 次数的计算结果与真实情况比较接近。

5 碰撞次数的理论计算

第4 章中我们对CE 次数所做的理论计算也可以运用到对碰撞次数的计算上，只不过因为碰撞的时候两个小天体距离较近，引力偏折较大，因此，用上述碰撞截面计算方法得出的碰撞次数的精度会差一些。但至少我们可以用这种方法得出估算值的下限。

5.1 单个PL的情形

估算碰撞次数的方法其实与第4.1 节中估算CE 次数的方法完全一致，只不过需要改动阈值半径的定义。对于碰撞而言，阈值半径为两个小天体的物理半径之和，即：

其中，RP为PL 的物理半径，RT为TR 的物理半径。这样，继续应用式(3)，就可以得到单个PL 引起的总碰撞次数：

以冥王星的密度作为标准，将PL 的物理半径表示为其质量的关系式，即：

其中，RPluto为冥王星的半径。所以式(20)可表示为：

类似于描述近密交会次数的式(6)，总的碰撞次数Nco与PL 质量也大致成2/3 幂次关系，说明当PL 总质量固定时，PL 的个数越多，总的碰撞次数也越多，符合一般认知。

5.2 一群PL的情形

下面估算一群PL 所引起的碰撞次数。同样，先按照式(11)和式(12)定义PL 的质量分布函数f(νP)，然后根据式(13)，估算总的碰撞次数：

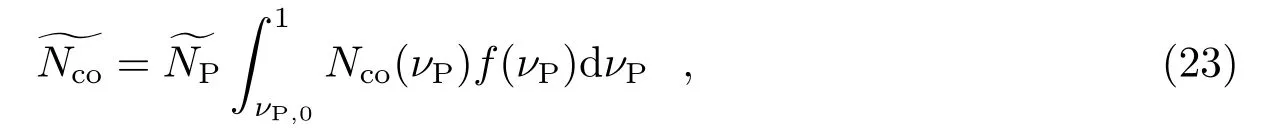
其中，νP,0是积分下界。

在碰撞问题中，积分下界较难确定，因为即使PL 的质量很小，它也可以与TR 发生碰撞，只不过碰撞所引起的效果不大。实际上，针对不同的实际问题，此标准应该随时变化。

6 实际情况

我们利用本文所得到的半解析结果来计算实际发生在PL 与TR 之间的近密交会和碰撞次数。

6.1 PL的质量分布

我们首先对PL 的质量分布进行计算。我们先从IAU 小行星中心[1]获取所有已经被证认的101 个PL 的数据。实际上，仅有少数几个PL 的质量有较准确的观测数据，如冥王星以及Orcus,Ixion,2003 AZ84,2003 VS2 等。由于反照率未知，其质量很难准确给定，因此我们这里使用近似方法来估算PL 的质量，即把PL 的行星绝对星等转化为其物理半径，然后再根据冥王星的平均密度计算其质量。计算结果如图5所示。

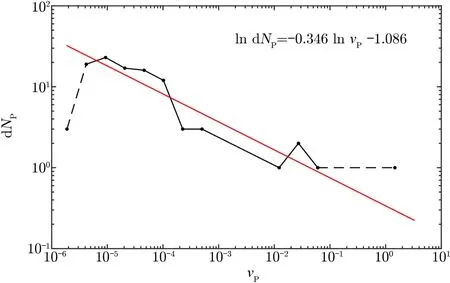
图5 由观测数据计算得到的PL 的质量分布

由图5可知，由实际观测数据计算得到的PL 质量分布的频率大致与质量成简单的幂律关系，即：

该式也可以写作：

其中，B0是归一化系数。这方便了后面的相关计算。

6.2 近密交会次数

根据以上理论结果，我们可以对实际情况下TR 与PL 之间的CE 次数进行计算。我们主要计算某一个TR 受到真实的PL 群CE 摄动的次数。当然，若要反过来估计TR 群对PL 的影响，也可以做同样的推算。作为一个例子，我们推算一个半径为100 km 的TR 所受到的PL 群的CE 摄动次数。

假设除冥王星外所有PL 的总质量不超过冥王星的质量(这是一个合理的估计)，这样，PL 群的总质量为另外，实际情况下PL 的最小物理半径应大于冥王星半径的10−6，也就是说，在1 m 量级左右。比这个尺寸小的PL 产生的摄动效果太小，可以忽略。因此

由式(12)的总质量关系式，以及式(25)的质量分布函数，我们可以得到：

由于νP,b非常小，可忽略不计，因此，我们得到系数

这样，根据式(15)，我们可以得到总的CE 次数：

其中，我们忽略了νP,0项。

由图2和图3可知，当νP=1 时，最优轨道条件下CE 次数在104左右。这样，根据式(6)可以算得，在最优轨道条件下χN=104。在此情况下，也就是说，在1 Ga 内，一个TR 受到总质量为2 个冥王星质量的PL 群的近密摄动次数约为4×104。

我们可以进一步讨论各个质量区间对总CE 次数的贡献，以获得一个基本的认识。由式(14)可以得到，某一质量区间[νP−∆νP,νP]贡献的CE 次数是：

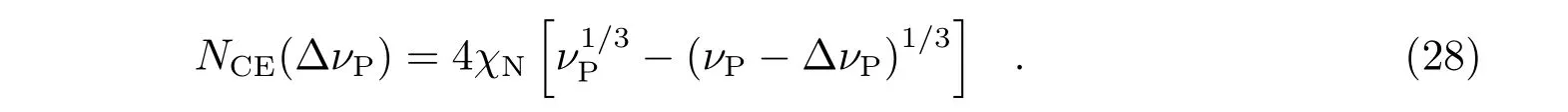
由此可得，半径在100～1 000 km 量级的PL 对总CE 次数的贡献约为3.6×104，而半径小于100 km 的PL 对总CE 次数的贡献为剩余的4×103。这说明大质量PL 贡献的CE 次数占总CE 次数的90% 以上，在整个CE 的演化中起着决定性的作用。

6.3 碰撞次数

用类似的方法也可以计算PL 与TR 的碰撞次数。由计算碰撞次数的式(20)可以看出，要计算Nco，首先要求出与轨道性质有关的RU。仍然考虑轨道条件最优的情况，也就是χN≈104，由式(7)可得，RU≈0.001 4 AU≈2×105km。对实际的PL 和TR 来说，RU≫RP+RT。由式(20)可知，单个PL 与TR 的碰撞很难发生。

对于某个TR 受到一群PL 碰撞的情况，不妨取TR 半径为RT=100 km，并且PL 的总质量仍然假设为冥王星质量的2 倍，也就是由式(23)可得，单个TR 与质量分布为f(νP)的一群PL 的总碰撞次数为：

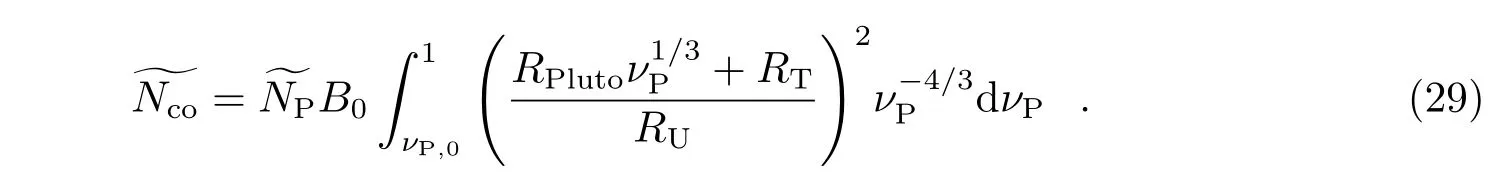
经简单计算可得：

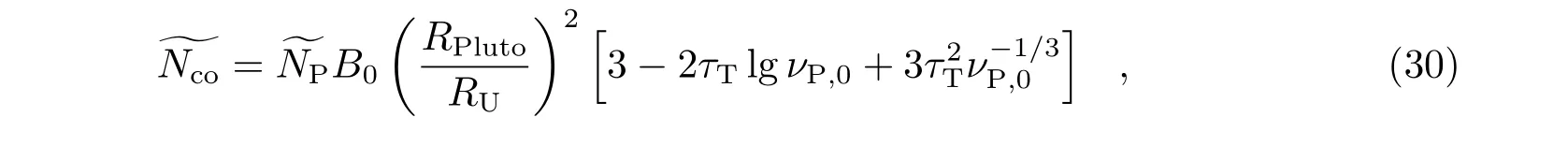
其中，τT=RT/RPluto。考虑到νP,0≪1，我们略去了一些常数项。另外，由总质量的归一化条件，我们容易得到

现在需确定积分下界。既然考虑的是半径为102km 量级的TR 的碰撞，我们不妨把碰撞的下界确定为质量分布的下界，即νP,0≈νP,b≈10−18，也就是在1 m 量级左右。这样，我们最终可以得到：

也就是说，一个102km 量级的TR 在109a 内与总质量为2 倍冥王星质量的PL 群发生约1 次碰撞。这是一个非常小的概率，在TR 的演化中基本上可以忽略不计。

通过进一步计算我们还发现，这1 次碰撞是由半径最小的那一部分PL，也就是半径在1～10 m 量级的PL 引起的。这样的碰撞显然不会对TR 的演化带来决定性影响。

实际上，在νP,0≪1 的情况下，式(30)可写为：

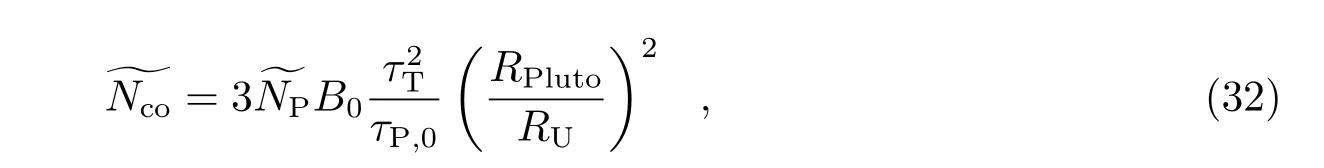
式(33)给出了可能与半径为τT的TR 在109a 内发生至少1 次碰撞的PL 半径的限制。

7 总结与讨论

我们改进了已有的数值模拟方法，使其能更加准确而有效地捕捉冥族小天体与海王星特洛伊这两群小天体之间的近密交会。在数值模拟的基础上，我们详细研究了各轨道参数以及小天体的大小和质量对近密交会频率的影响。我们发现，小天体的质量是影响CE 次数的决定性因素，两者的量级呈线性变化。PL 和TR 的倾角是影响CE 次数的次要因素，影响范围基本上是在1 个量级以内。理论上，PL 的偏心率也是影响CE 的决定性因素。实际观测到的PL 的偏心率大多满足发生CE 的基本要求(即能使PL 的近日点穿过TR 轨道)。而只要保证CE 发生，其偏心率的具体大小对CE 次数的影响便有限，所以，总体上PL 的偏心率对CE 的影响是较小的。另外，只有那些偏心率很小的TR 才能维持其轨道稳定性。实际上，并不存在大偏心率的TR，因此，本文未讨论TR 的偏心率大小对CE 次数的影响。最后，PL 和TR 的共振振幅对CE 次数的影响被证明是非常小的，并且当振幅增大时，这种影响还具有负效果，这与前人[2]的推测完全不同。

在经典的碰撞截面的基础上，我们提出了估算CE 次数的理论公式，并在忽略低质量小天体之间微弱引力的前提下，把这一公式推广到碰撞次数的估算上。当合理忽略轨道参数的影响时，我们将该公式进一步应用到了一群小天体间的碰撞次数估算上。

最后，我们以现有的PL 观测数据为基础，推导了PL 群的质量分布函数，并利用上述公式估算了实际情况下近密交会和碰撞次数。我们发现，一个典型TR 在109a 内与一群总质量不超过2 倍冥王星质量的PL 发生近密交会的次数在104量级，其中大部分交会是由半径在102km 量级以上的PL 贡献的。另一方面，我们发现，一个典型TR 在相同时间尺度内与同一群PL 发生约1 次碰撞，并且这1 次碰撞是由半径10 m 量级以下的PL 引起的，所以碰撞在典型TR 的动力学演化中所起的作用可以忽略不计。上述分析还说明，碰撞过程基本上是由小尺度天体引起的，而近密交会则几乎只与大质量天体有关。

我们主要讨论了PL 对TR 的作用。用同样的方法也可以研究TR 对PL 的影响。只是由于目前TR 的观测数据很少，很难对实际情况下TR 的质量分布做出计算，所以暂时无法研究TR 群对PL 的动力学影响。

另外应该指出的是，我们的分析过程完全可以应用到其他任意两群小天体之间近密交会和碰撞频率的估算上，只要这两群小天体的轨道保持相对稳定，比如小行星主带中分别处于与木星发生3 :2 和1 :1 轨道共振处的希尔达群(Hilda group)和木星特洛伊，就是这样的例子。