利用GNSS测量射电望远镜参考点的仿真分析
刘 耘,陈卯蒸,刘志勇
(1.中国科学院 新疆天文台,乌鲁木齐 830011;2.中国科学院 射电天文重点实验室,南京 210008;3.中国科学院大学,北京 100049)
1 引 言
地球参考框架是地球参考系统的具体实现,国际地球参考框架(ITRF)是最精密的地球参考框架,是对甚长基线干涉测量(VLBI)、卫星激光测距(SLR)、全球卫星导航系统(GNSS)、多普勒定轨和无线电定位技术(DORIS)等多种空间大地测量技术的观测数据进行综合处理后建立起来的。对并置站各空间测地技术参考点之间的三维坐标差,即本地连接参数[1,2]可进行这种综合处理。要获得本地连接参数需要精确测量各测站参考点的坐标和轴线偏差。同时,完成天线参考点的精确测定也是建立天线指向模型的重要前提。射电望远镜的参考点是一个几何点,通常位于设备内部,无法直接测量。
目前对VLBI 天线参考点的测量方法主要分为以下三种。(1)测地VLBI 方法[3,4]。待测站与具备高精度测站坐标的台站构成基线,通过观测高精度坐标已知的河外射电源,就能解算出待测站天线参考点的坐标。测地VLBI 方法精度最高,通过积累多年数期的VLBI联测资料,可不断提高测站坐标的精度。(2)常规静态归心测量法[5–11]。在天线周围布设局域控制网,通过常规大地测量获得各测点的本地坐标。利用GNSS 测量各测点的地心3D 坐标,经数据解析得到本地坐标与地心坐标之间的转换关系。以局域网中的测点为基准,使用全站仪测量望远镜上靶标的本地坐标。以方位俯仰型天线为例,测量方位轴的数据点时,设俯仰角不变,且望远镜以特定的方式绕方位轴旋转,人们通过对采集的数据点进行空间圆拟合可以确定方位轴的位置和方向;采用类似的方式还可以确定俯仰轴的位置和方向。根据方位轴和俯仰轴的空间关系可以解算出参考点坐标和轴线偏差。常规静态归心测量方法需要在天线周围设立测量基墩,拟合出参考点坐标之后,还需要从本地坐标转换为地心坐标,因此测量过程较繁琐。(3)随机动态测量方法[12–17]。这是近年来提出的新方法,通过建立天线上某点的坐标与天线参数和天线指向的数学模型,以天线的方位角和俯仰角作为已知量,获得天线在不同方位俯仰时的数据,从而解算出天线的参数。随机动态测量方法不再限定天线以特定方式旋转,无需额外占用天线的正常观测时间就可以实现对天线参考点和轴线偏差的测量与监测。在随机动态测量方法的数学模型中,我们将天线的俯仰角和方位角作为已知量进行数据解算,这对于还未精确建立指向模型的新建望远镜并不适用[11]。结合常规静态测量方法和随机动态测量方法,本文提出一种以GNSS 天线代替测量靶标从而实现天线参考点测量的方法,能够快速测定新建射电望远镜参考点的初始参考值。为了验证该方法的可行性,我们对模拟数据进行了仿真分析,并研究了数据点个数和数据点测量精度对天线参数解算精度的影响。
2 方法与模拟数据
2.1 方法
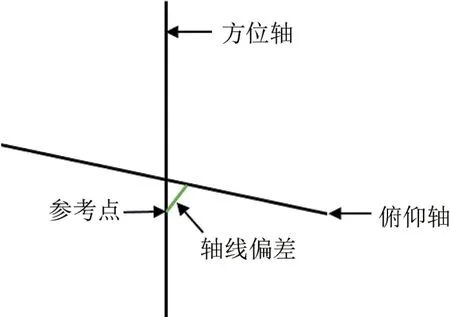
图1 方位俯仰型天线参考点示意图
射电望远镜的参考点定义为俯仰轴和方位轴的公垂线在方位轴上的垂足,公垂线的长度即为轴线偏差[6]。本文以方位俯仰型天线为例,方位俯仰型天线的参考点如图1所示。天线的俯仰轴绕方位轴旋转,天线绕俯仰轴和方位轴旋转。在测量时将两个GNSS 天线安装在望远镜主反射面两侧边缘的位置[15],利用铅垂仪的方式安装GNSS 天线,可确保望远镜在不同的方位俯仰时,GNSS 天线始终指向天顶,并避免天线对GNSS 信号的遮挡和干扰。射电望远镜在两种不同的旋转方式下利用GNSS 采集数据。第一种为望远镜绕某个轴以特定的方式旋转。当天线俯仰角固定及望远镜绕方位轴旋转时,GNSS 天线的运动轨迹是空间圆;当天线方位角固定及望远镜绕俯仰轴旋转时,由于射电望远镜受结构的限制,GNSS 天线的运动轨迹是空间圆上小于1/4 的圆弧段。另一种是射电望远镜随机旋转。因为望远镜方位角在0◦~360◦之间变化,而俯仰角的变化范围是5◦~88◦,所以GNSS 天线采集的点是球体上的带状区域内的散点。我们利用第一种旋转方式下获取的数据点,对望远镜绕方位轴和俯仰轴旋转得到的数据点分别进行空间圆拟合,并根据拟合空间圆的圆心和空间圆所在平面的法向量确定方位轴及俯仰轴的方向和位置;再根据方位轴和俯仰轴的空间位置关系解算出望远镜的参考点坐标和轴线偏差。我们利用第二种旋转方式下获取的数据点进行球体拟合,得到的球心坐标即为望远镜的参考点坐标。第二种采集数据点的方法可用于连续监测射电望远镜参考点。我们拟采用徕卡GR50 接收机。徕卡GR50 的静态定位精度是平面为3 mm+3×10−7D(rms),高程为5 mm+3×10−7D(rms);动态测量精度是平面为8 mm+1×10−6D(rms),高程为15 mm+1×10−6D(rms),D表示测量的距离。扼流圈天线具有出色的抑制多路径功能,但是质量较大,不利于安装加工,因此拟采用质量较小的徕卡AS10 天线。
2.2 模拟数据
本文以南山26 m 射电望远镜为基础,构造口径为26 m,参考点的地心坐标为(228 310.252 3,4 631 922.754 9,4 367 064.046 2)m 的方位俯仰型望远镜,根据望远镜的旋转模型产生模拟的数据点。在距离射电望远镜大约200 m 的地方有GNSS 基准站,在测量时以GNSS 基准站作为基准。俯仰角α分别为25◦和88◦,方位角以20◦间隔改变时,一个GNSS 天线获取的模拟数据如表1所示。望远镜在4 个不同的方位时,俯仰角在10◦~88◦内以固定的角度间隔改变,模型分别生成4 组模拟数据,其中每组数据包括两个GNSS 天线获取的数据点。俯仰角以10◦间隔改变时,一组由模型所生成的模拟数据如表2所示。望远镜随机旋转时,模型所生成模拟数据中的60 个数据点如表3所示。
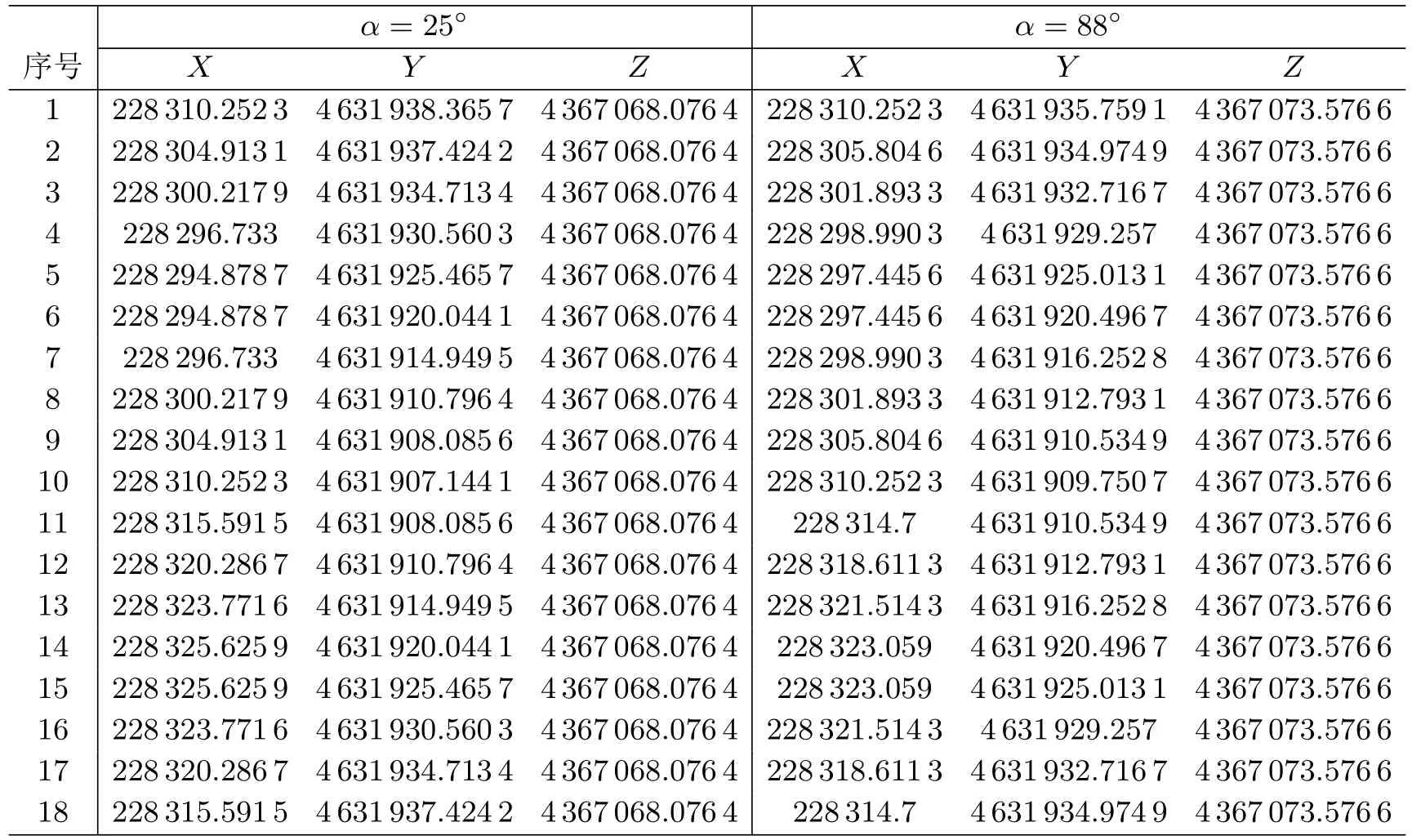
表1 俯仰角分别为25◦和88◦时方位角以20◦间隔改变生成模拟数据的点坐标 m

表2 方位角固定,俯仰角以10◦间隔改变生成模拟数据的点坐标 m
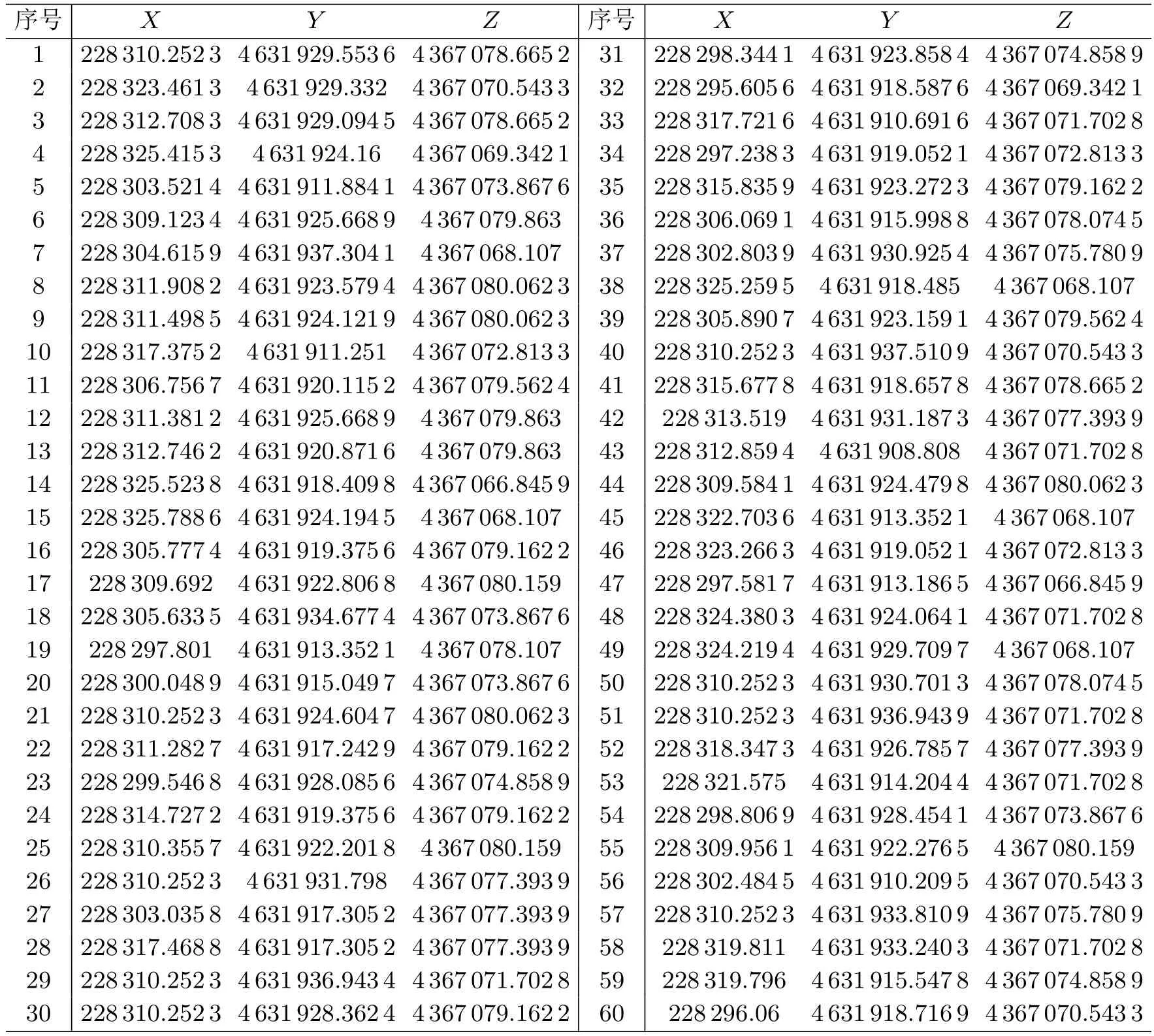
表3 望远镜随机旋转时生成模拟数据的其中60 个点坐标 m
3 拟合与仿真分析
李金岭等人[9]拟合空间圆时,先拟合出空间圆所在的平面,之后将点位坐标旋转至临时坐标系,并在此平面内对圆进行二维拟合,然后再将得到的圆心坐标旋转后,得到最终的圆心坐标。这种拟合方法涉及坐标系旋转,计算过程较繁琐。我们采用潘国荣和陈晓龙[18]提出的空间圆拟合方法,将空间圆看成是空间球面和空间平面的交线,先拟合出空间圆所在的平面,然后拟合空间球体,再根据几何关系解出空间圆的圆心坐标。利用望远镜随机旋转获取的数据,我们可根据球面上带状区域的散点分布直接拟合球心坐标。
3.1 单轴旋转的拟合
我们对俯仰角为25◦和88◦的模拟数据分别进行空间圆拟合,生成模拟数据的点坐标如表1所示。考虑到GNSS 天线的快速静态定位精度,我们在拟合时对原始模拟数据的坐标分量分别附加10 mm 的随机误差,然后得到空间圆的圆心坐标和空间圆所在平面的法向量。由于两个空间圆平面的法向量的加权平均值为方位轴的方向向量,并且两个空间圆圆心坐标的平均值作为方位轴上的一点,因此我们可以确定方位轴的方程。对方位轴的直线方程和空间圆所在的平面方程进行求解,得到的方位轴线段上的两个端点坐标为:

我们对望远镜绕方位轴旋转时模拟数据点的空间圆以及方位轴测量线段进行了拟合,结果如图2所示。
类似地,以表2中的数据为例,我们对望远镜绕俯仰轴旋转时模拟数据点的空间圆进行了拟合(见图3),并得到俯仰轴测量线段的端点坐标:

由式(1)和式(2)可解得公垂线在方位轴上的垂足w1及轴线偏差(公垂线长度)f1,具体计算方法参考文献[7],

对模拟数据点进行空间圆拟合时的拟合残差是反映拟合误差的重要指标,以图3中的数据点为例,表4给出各个点的wrtp和wrtc,分别表示点相对于空间圆所在平面的距离(平面上方为正)和在圆所在平面内至拟合圆周的距离(圆外为正)[11]。由表4可以看出,各个点的总体残差小于17.32 mm,这与坐标分量所附加的10 mm (三维位置误差约为17.32 mm)随机误差一致,表明空间圆的拟合结果是可靠的。参考点w1和轴线偏差f1的拟合结果见图4。
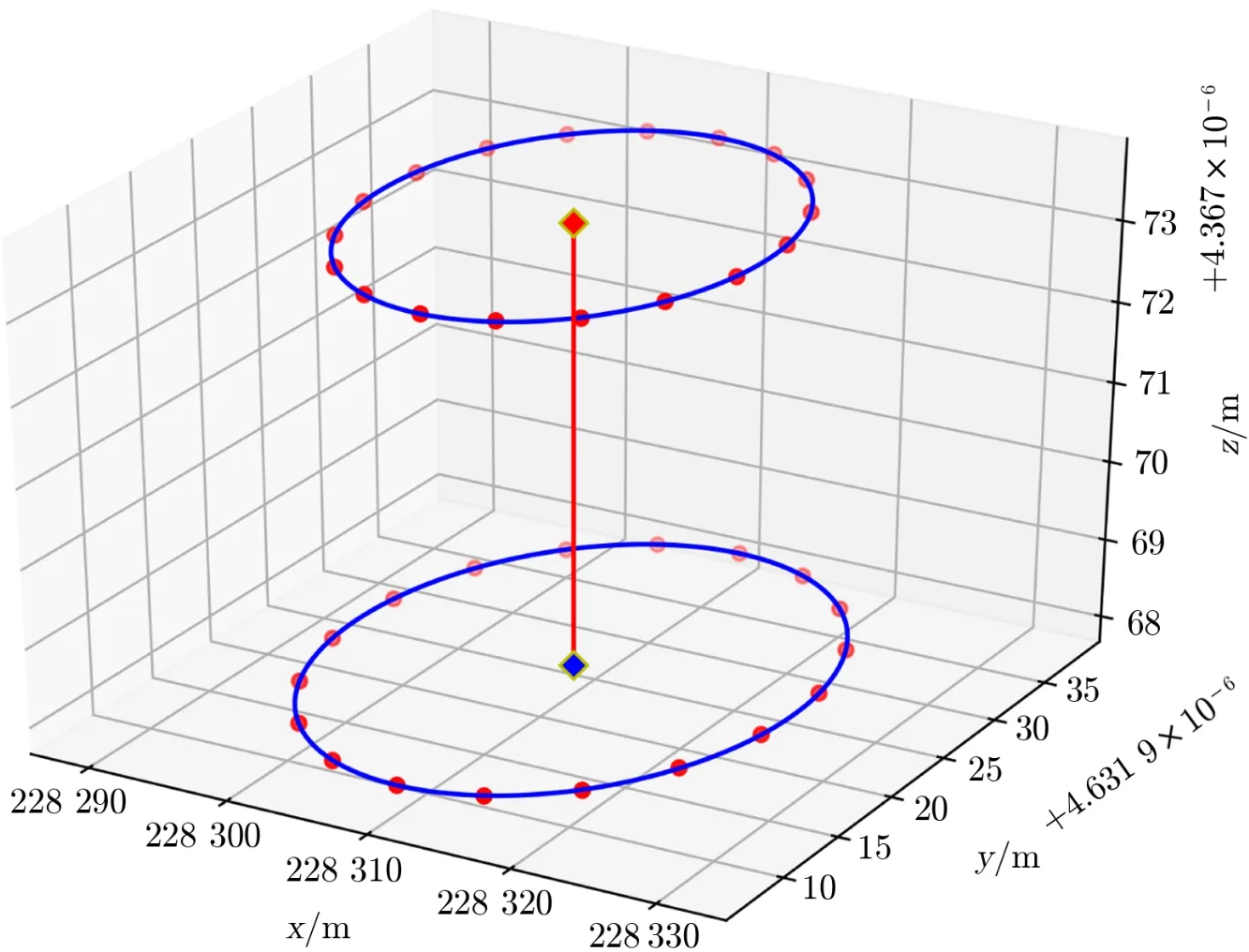
图2 方位轴拟合
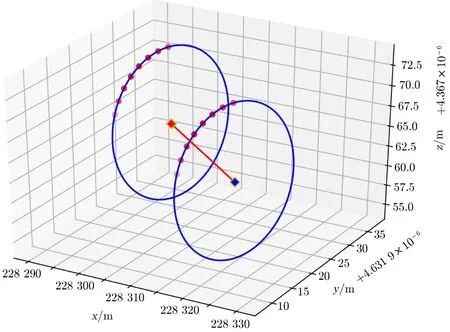
图3 俯仰轴拟合
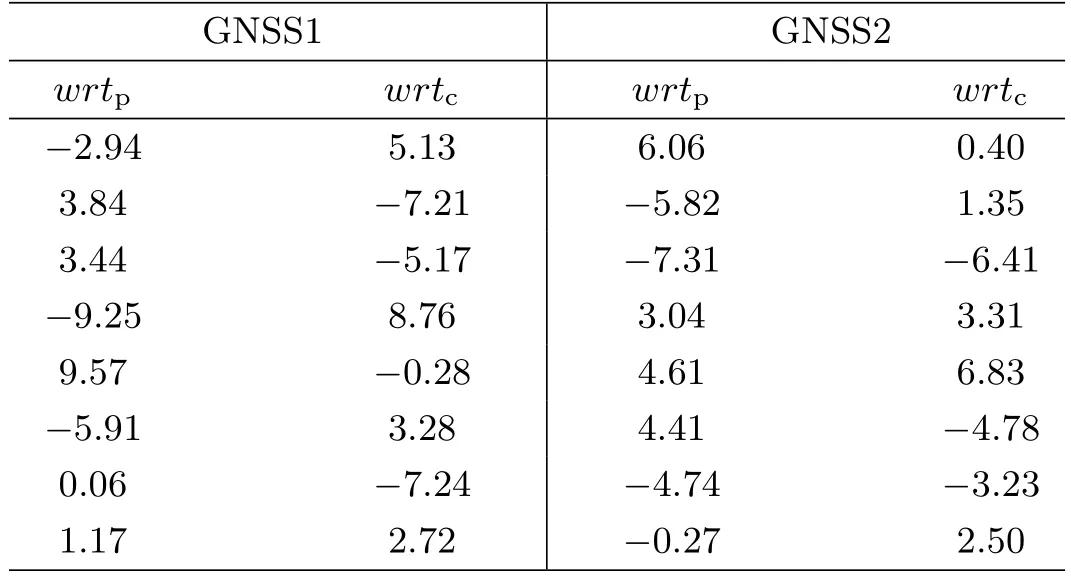
表4 图3中空间圆拟合残差 mm
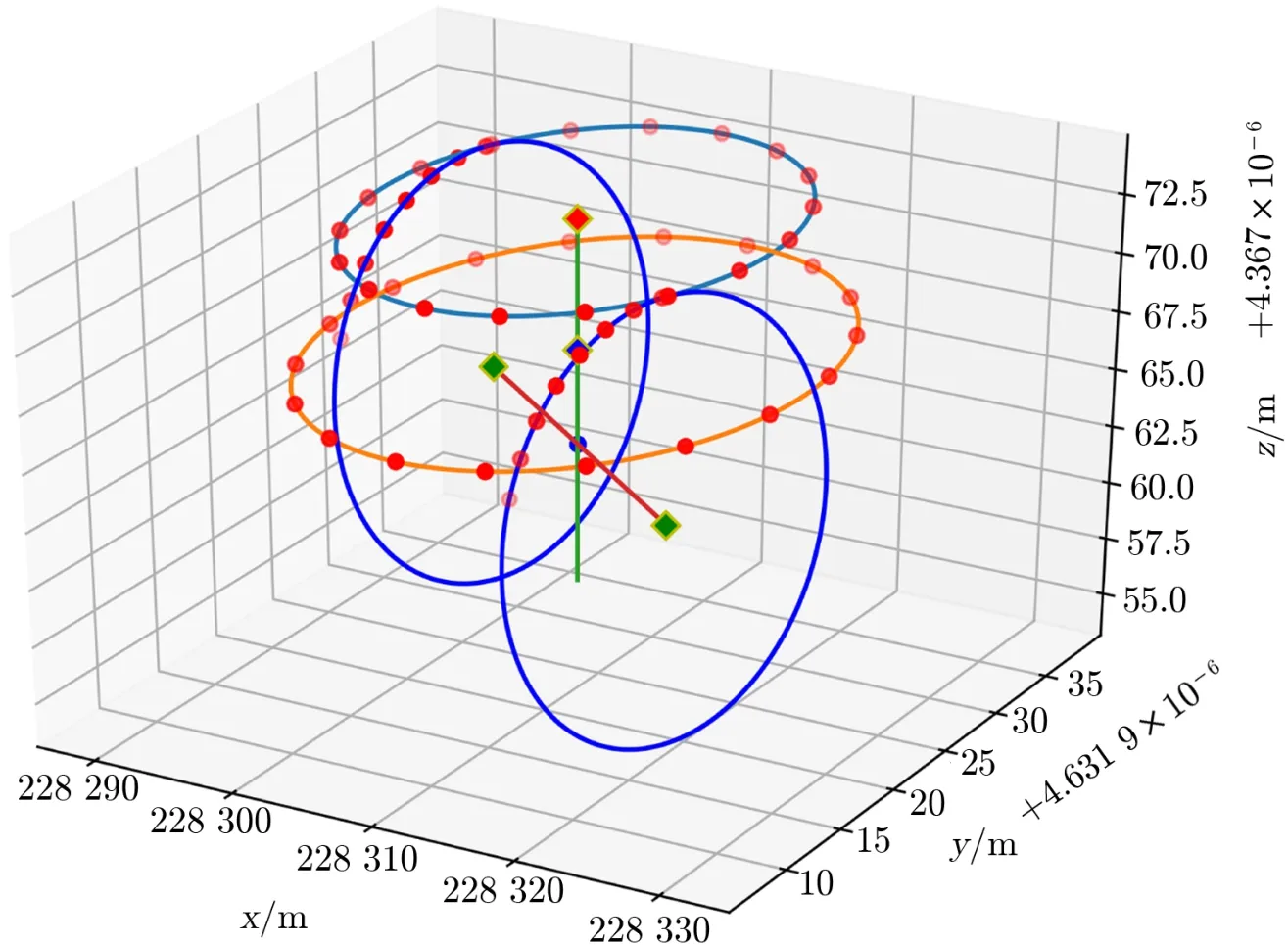
图4 参考点及轴线偏差的拟合
我们对另外三个方向俯仰轴的模拟数据进行了类似的处理,对于在不同方位下解算的参考点坐标和轴线偏差加权取平均,得到的结果就是最终的参考点坐标w和轴线偏差f。本文得到的参考点是在WGS84 系统下的地心坐标,

3.2 随机旋转的拟合
我们对表3的数据进行球拟合。考虑到GNSS 天线的单基线RTK 定位精度,在拟合时对原始模拟数据的坐标分量分别附加15 mm 的随机误差。拟合得到的球心坐标即为参考点RP的坐标:
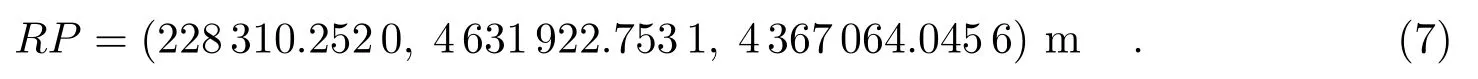
图5给出球体上数据点的分布与参考点的拟合情况,其中红色的点代表模拟数据点,绿色的点为拟合得到的参考点。
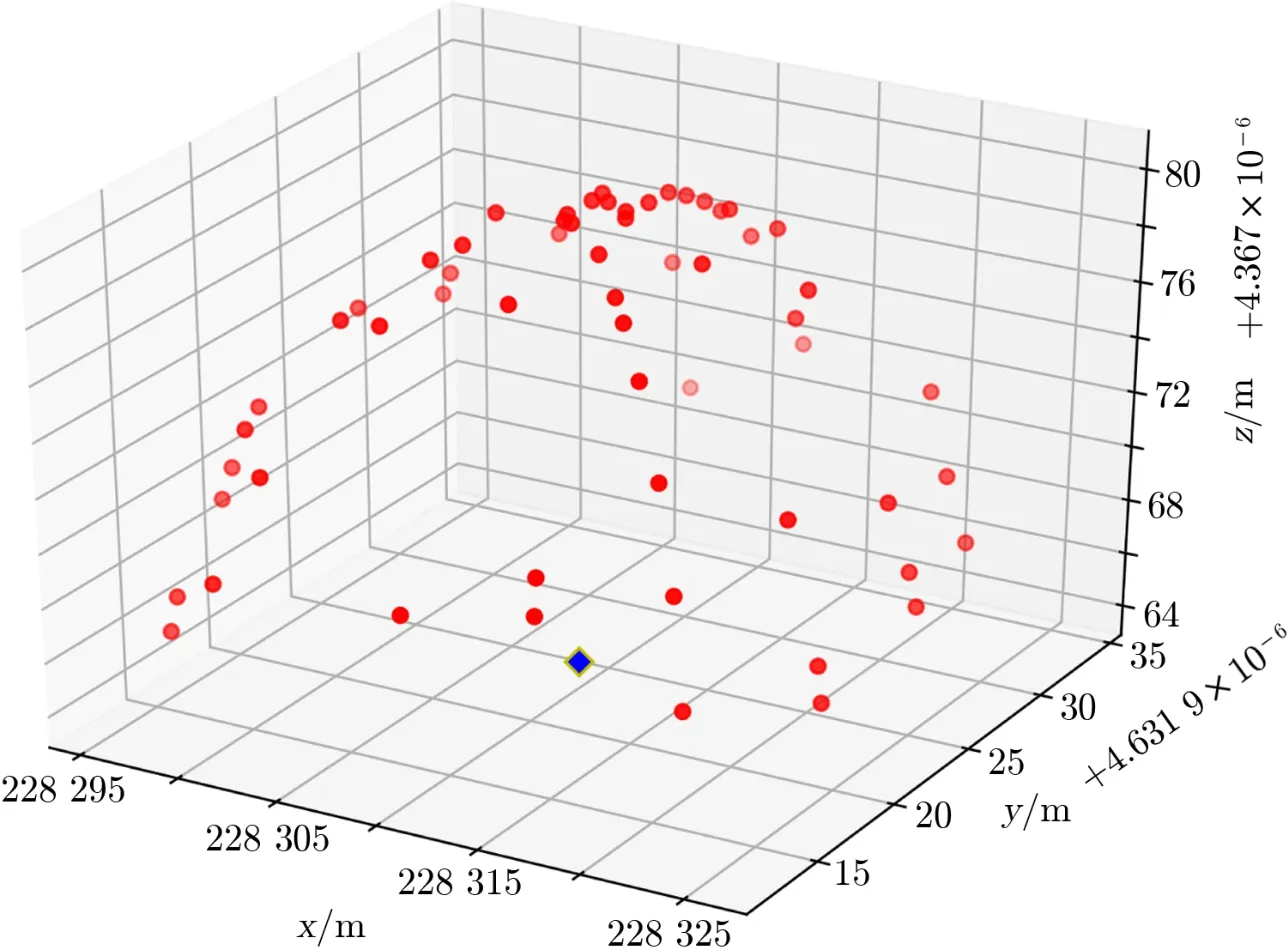
图5 球体上数据点分布与参考点拟合
由式(5)和(7)可知,望远镜在两种不同旋转方式下对生成模拟数据点进行了拟合,得到的参考点坐标和参考点真值坐标偏差分别约为2.95 mm 和1.92 mm。这两种拟合方法中各个点的拟合残差与所附加的随机误差基本一致,因此两种拟合方法都有效。
3.3 参数拟合精度分析
利用上述拟合方法,我们分别研究了GNSS 采集数据的精度和个数对天线参数拟合精度的影响。
3.3.1 采集数据精度对天线参数拟合精度的影响
在单轴旋转方式下生成的模拟数据点的坐标分量中依次加入随机误差,从5 mm 逐次增加5 mm,直至50 mm,对不同误差下的数据分别进行50 次仿真计算取平均值。由于GNSS绕俯仰轴旋转形成的轨迹为空间圆上小于1/4 的圆弧段,当数据点很少进行空间圆拟合时,所附加的随机误差会对拟合结果产生显著的影响,因此选用方位角间隔2◦依次改变生成的数据点和俯仰角间隔1◦依次改变生成的数据点进行模拟计算。参考点的偏差为解算的参考点坐标与参考点坐标真值之间的距离,轴线的偏差为解算的轴线偏差与真值之差的绝对值。如图6所示,随着不断增加随机误差,参考点坐标的偏差和轴线的偏差近似呈线性增加。
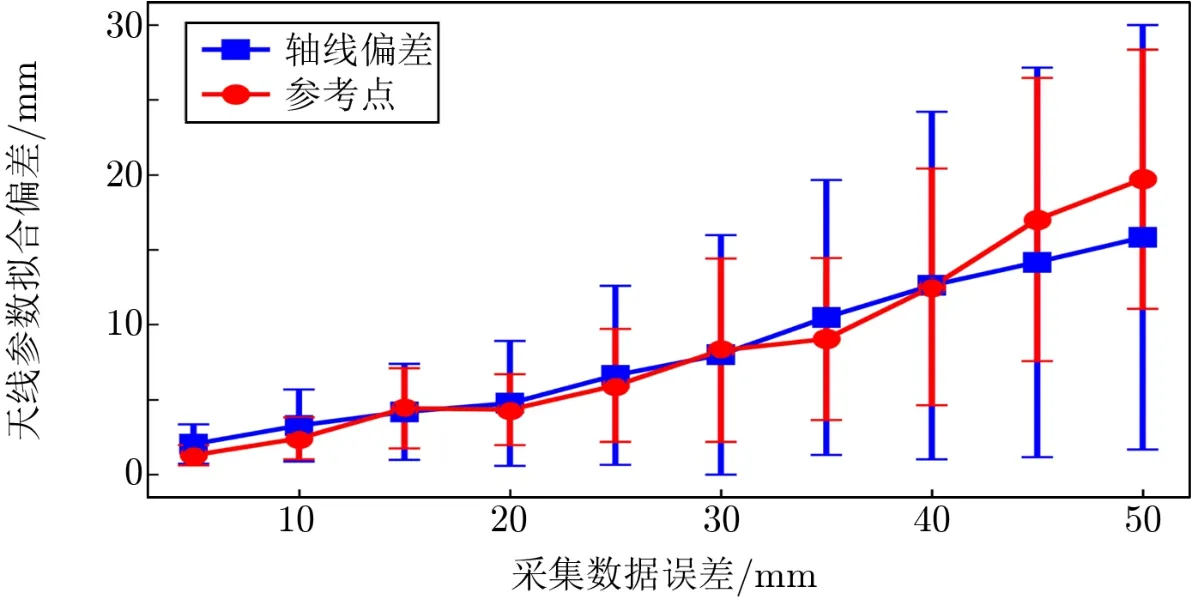
图6 天线参数拟合精度随采集数据误差的变化
在随机旋转方式下,对生成的300 个模拟数据点的坐标分量依次加入随机误差,从15 mm 逐次增加5 mm 至50 mm,对每个误差下的数据进行50 次仿真计算并取平均值。我们得到不同精度下采集数据与天线参考点的拟合精度的关系,以及相同误差的采集精度下单轴旋转方式与随机旋转方式解算参考点精度的对比,如图7所示。
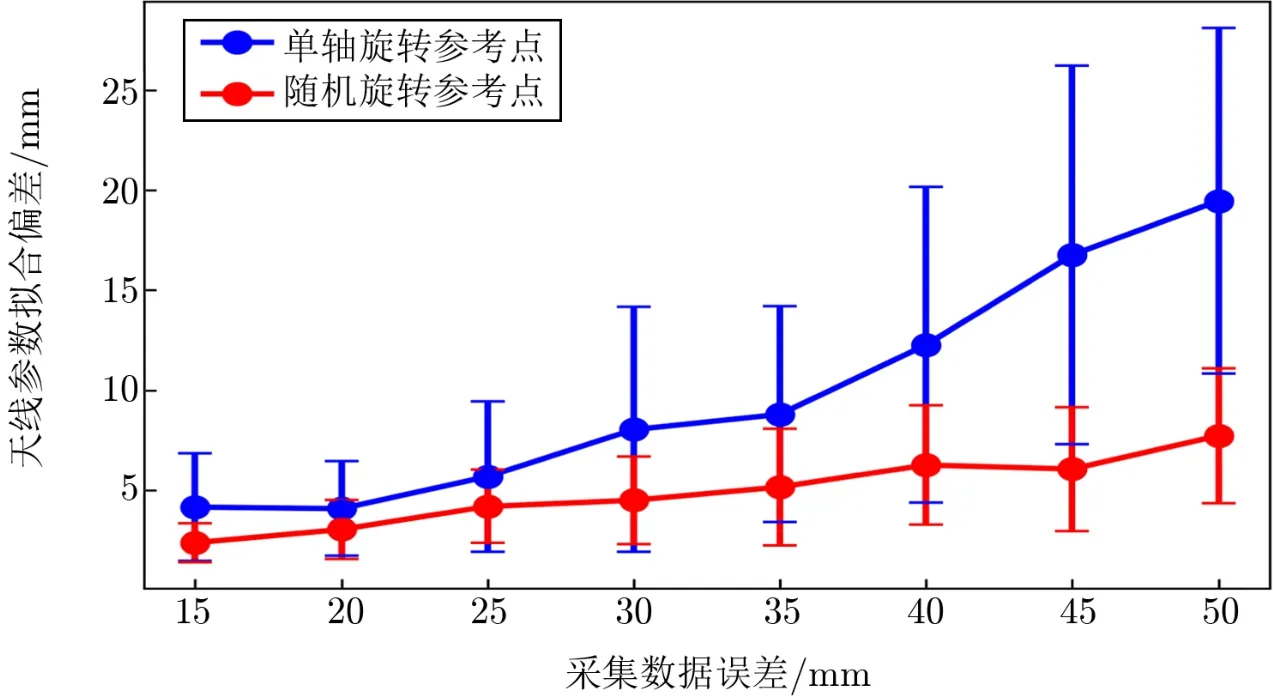
图7 两种不同数据采集方式在不同误差下参考点解算精度的比较
在随机旋转方式下,参考点的偏差随着采集数据误差的增加而增加;采集数据的误差相同时,随机旋转方式解算的参考点比单轴旋转解算的参考点偏差要小很多,这是因为单轴旋转拟合时误差会累积,随机误差的不断增大对1/4 圆弧段的拟合影响越来越大。由图6和图7可以看出,在采集数据点个数相同的条件下,天线参数的拟合精度由采集数据的精度决定。因此,在测量射电望远镜参考点坐标时,要尽可能提高GNSS 天线的定位精度。
3.3.2 数据个数对天线参数拟合精度的影响
在单轴旋转的数据采集方式下,我们将所有的模拟数据点坐标分量都加入10 mm 的随机误差,并研究拟合数据点的个数对天线拟合参数偏差的影响,然后对每组数据分别进行50 次仿真计算并取平均值。我们还研究了采集的数据点个数的不同对天线参数拟合精度的影响,结果如图8所示,可见随着采集数据个数的增加,天线参数拟合偏差逐渐减小。
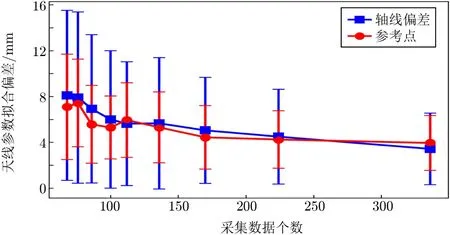
图8 天线参数拟合精度随采集数据点个数的变化
在射电望远镜随机旋转的数据采集方式下,由于随机旋转采集的数据点位置不同对拟合结果会有影响,我们随机取数据点分别进行模拟计算。数据点个数从50 逐次增加30 至320,所有的数据点都附加15 mm 的随机误差,我们对每组数据点进行50 次仿真计算并取平均值。仿真结果如图9所示。
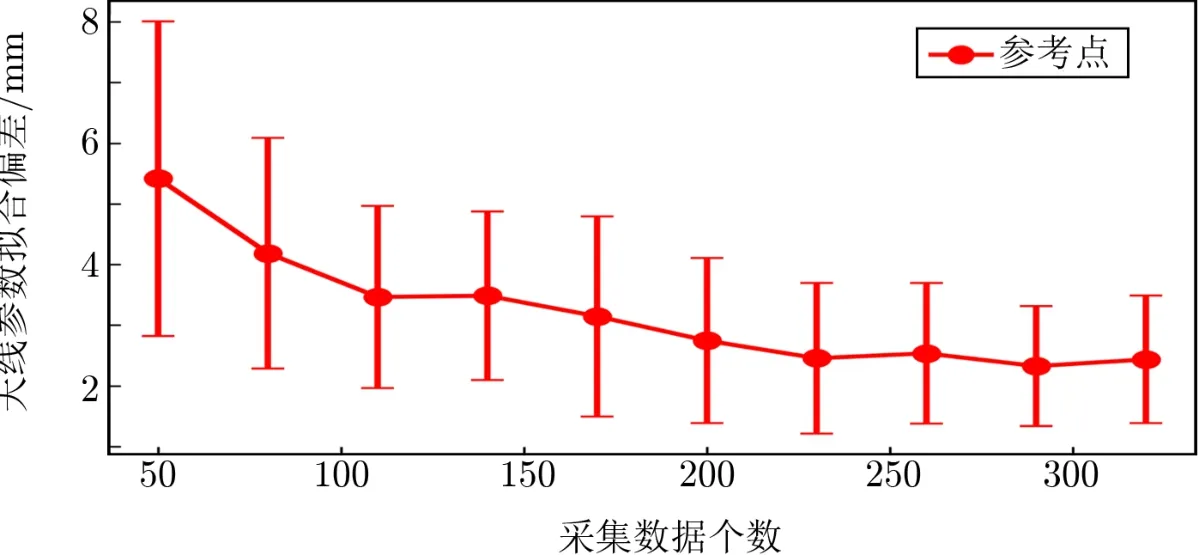
图9 参考点偏差随采集数据点个数的变化
由图8和图9可知,天线参数拟合偏差随着采集数据个数的增加而减小,当采集数据个数增加到一定数量时,天线参数拟合偏差变小的速率会逐渐减慢并趋向于平缓。要进一步提高天线参数的拟合精度,需要通过其他方法,如提高采集数据的精度。
4 结论与讨论
上述分析与模拟结果表明,通过在射电望远镜主反射面边缘安装GNSS 天线采集数据点,进行空间圆拟合解算参考点坐标和轴线偏差,该方法在理论上是可行的。常规静态测量方法需要在天线周围设立测量基墩,其涉及坐标系之间的转换,且测量过程较繁琐。采用随机动态测量方法,我们不必额外占用望远镜的正常观测时间即可实现对射电望远镜参考点的监测。采用随机动态方法建立的数学模型中天线的方位角和俯仰角是作为已知量进行输入并解算天线参数,对于还未建立准确的指向模型的新建射电望远镜并不适用。本文提出的方法可以快速测定新建射电望远镜参考点坐标的初始参考值。但是,本文的模拟数据生成和仿真计算可能过于理想化,实际测量中由于GNSS 天线具有多路径效应,GNSS 天线在运动中被望远镜遮掩,因此GNSS 天线的相位中心将变化,射电望远镜主反射面变形,射电望远镜轨道面不平,数据传输等方面的问题都会影响天线参数的解算精度。总之,本文的分析结果有待进一步检验,后续我们将在新疆天文台南山26 米射电望远镜上进行实验,验证方法的可行性和测量精度。

