BDS-2导航电文的TGD参数精度及其对用户导航定位精度的影响

吴 竞，唐成盼，周善石，胡小工，董文丽

(1.中国科学院上海天文台，上海 200030；2.中国科学院大学，北京 100049)

1 引言

卫星从发出信号至信号到达天线相位中心，所花时间称为硬件时间延迟。因为同一卫星不同频点或者不同信号分量的发射链路并不相同，所以不同频点或者信号分量之间存在DCB。IGS/MGEX 分析中心和导航电文分别播发DCB和TGD以消除不同频点或者信号分量的发射时延差。DCB的精确确定对电离层电子总含量的解算、授时和定位都有重要意义。

就GPS 系统而言，GPS 系统导航电文和IGS 精密钟差基准是L1 和L2 频点的P 码无电离层组合。GPS 双频用户无需改正TGD和DCB，而单频用户需要改正TGD和DCB后才能进行定位解算[1]。王宁波等人[2]通过计算发现，GPS 广播的TGD精度高于0.5 ns。BDS-2 播发B1,B2,B3 共3 个频点的信号，导航电文的钟差参数以B3 频点为基准，为正确使用钟差参数，北斗广播星历给出TGD1，供B1 频点的单频用户对钟差参数进行修正；还给出TGD2，供B2 频点的单频用户对钟差进行修正[3]。因此，B1 和B2 单频用户和双频用户均需使用TGD对伪距进行修正。BDS-2TGD最初使用的是发射前的出场标定参数。为反映卫星的实时在轨状态，TGD会进行实时解算更新，首先利用实测数据获取B1与B3 的双频伪距差和B2 与B3 的双频伪距差；再根据已知的电离层信息，同时求解出卫星和接收机的组合硬件延迟[4]。DCB一般由GNSS 数据处理机构事后处理得到，是供用户进行硬件延迟改正的事后精密产品。随着MGEX 试验的顺利进行，目前全球配备新型接收机的测站有200 多个，在全球范围内监测北斗系统，这为精确确定北斗的DCB参数提供了有力的保证。利用IGG-DCB方法得到的北斗DCB参数精度为0.36 ns，稳定性指标为0.17 ns[5]。Guo 等人[6]提出DCB参数计算的提升算法，用该算法计算得到的DCB参数精度为0.21 ns。目前，MGEX 综合了多个机构计算得到的北斗DCB，并对外发布，精度高于0.3 ns[4−5]。

MGEX 提供的DCB精度较高，可作为计算TGD的基准。MGEX 的TGD精度为2.6 ns，明显低于GPS 卫星播发的TGD精度[7]。DLR 的TGD精度为1.2 ns，同样低于GPS 卫星播发的TGD精度[8]。BDS-2 播发的导航电文存在偏差，该偏差是由广播电文中的TGD偏差造成的。将北斗广播星历偏差改正到TGD上，双频用户的单点定位精度将会提高，定位残差也将变小[6]。

本文首先总结了北斗群延迟和差分码偏差参数的改正模型；随后计算了BDS-2 卫星的TGD参数精度，并得到BDS-2 卫星群延迟参数的跳变及精度提高情况；最后分析了群延迟参数跳变对定位精度的影响。

2 北斗TGD/DCB改正模型

2.1 伪距观测方程

在利用北斗卫星定位的过程中，北斗B1,B2,B3 这3 个频点简化的伪距表示如下：

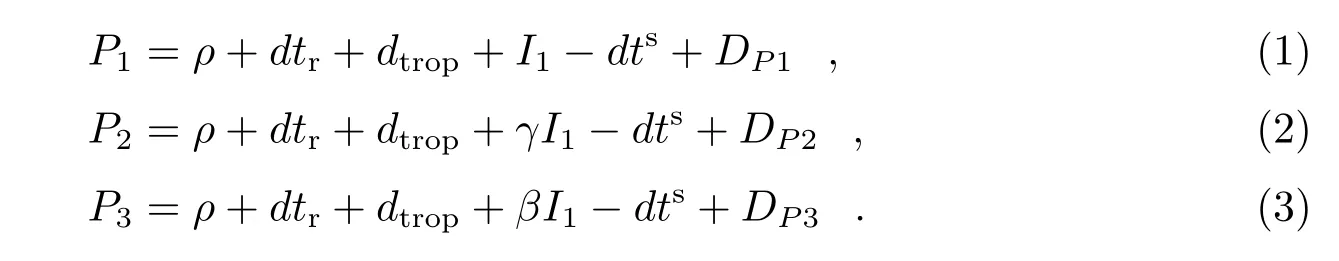
其中，ρ为星地之间的实际距离，dtr为由接收机钟差引起的伪距变化量，dtrop为对流层延迟引起的伪距变化量，I1为B1 频点由于电离层延迟引起的伪距变化量，分别表示B1,B2,B3 频点的频率)，dts为由卫星钟差引起的伪距变化量，DP1,DP2,DP3分别为B1,B2,B3 频点由于硬件延迟引起的伪距变化量。由于接收机的硬件延迟量被接收机钟差吸收，DP1,DP2,DP3实际表示由卫星硬件延迟造成的伪距变化量。

2.2 基于广播星历钟差的TGD/DCB改正模型

与GPS 不同，北斗广播星历的时空基准点为B3 频点[8]，因此北斗广播星历的钟差包含B3 频点的硬件延迟，即：

将式(4)代入式(1)―(3)中，可得下式：

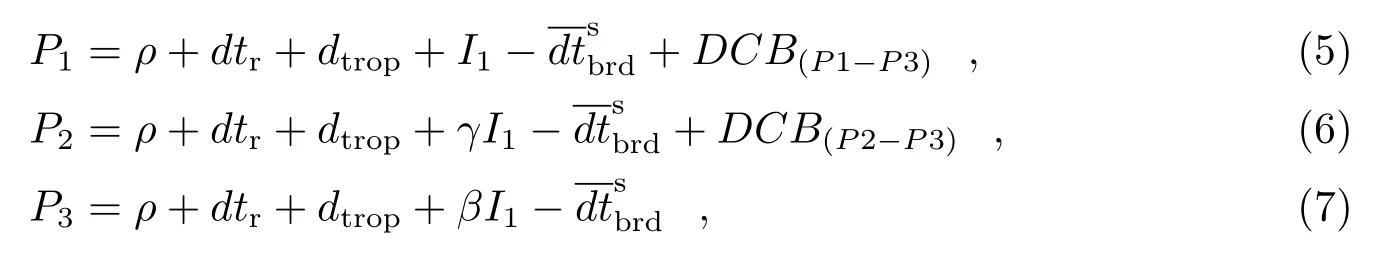
其中，DCB(P1−P3)表示B1 频点相对于B3 频点的硬件延迟，DCB(P2−P3)表示B2 频点相对于B3 频点的硬件延迟。

根据北斗播发的接口控制文件，B1,B2 频点的硬件延迟可用下式来改正：

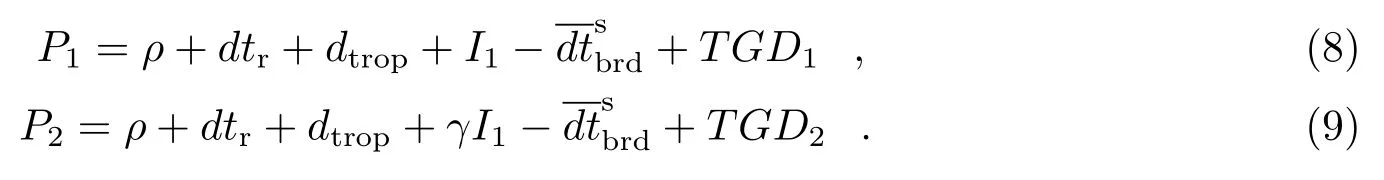
通过对比式(8)和(9)，可以得到北斗TGD和DCB的关系，表示如下：

对于双频无电离层组合用户而言，硬件延迟的改正公式如下：

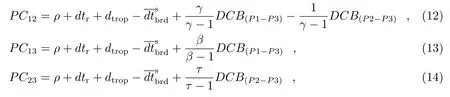
2.3 基于北斗事后精密钟差TGD/DCB改正模型

目前，北斗的精密轨道钟差产品都是基于B1,B2 无电离层组合计算得到的，故精密星历提供的钟差包含B1,B2 频点的组合硬件延迟。使用精密星历时，单频用户的硬件延迟改正为：

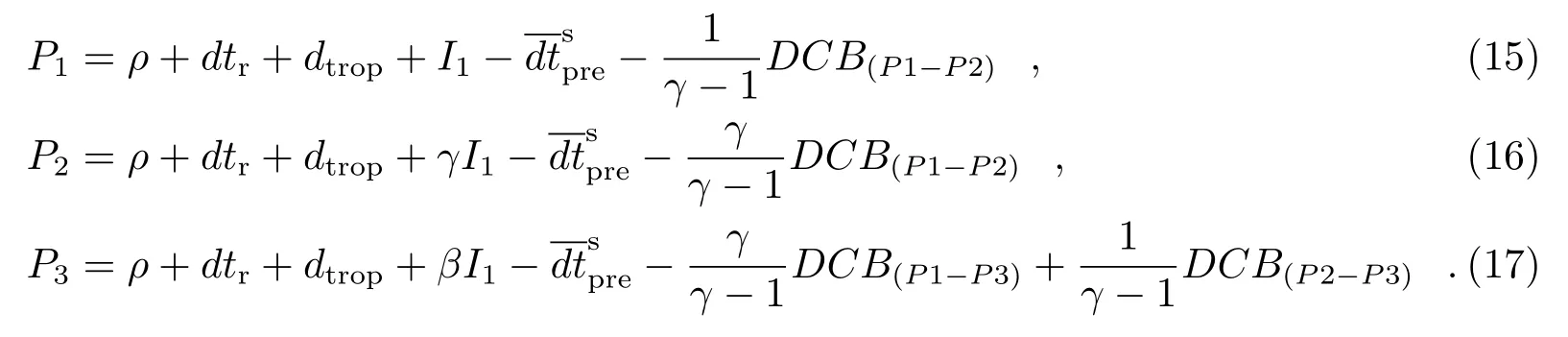
对于双频无电离层组合用户，硬件延迟改正如下：

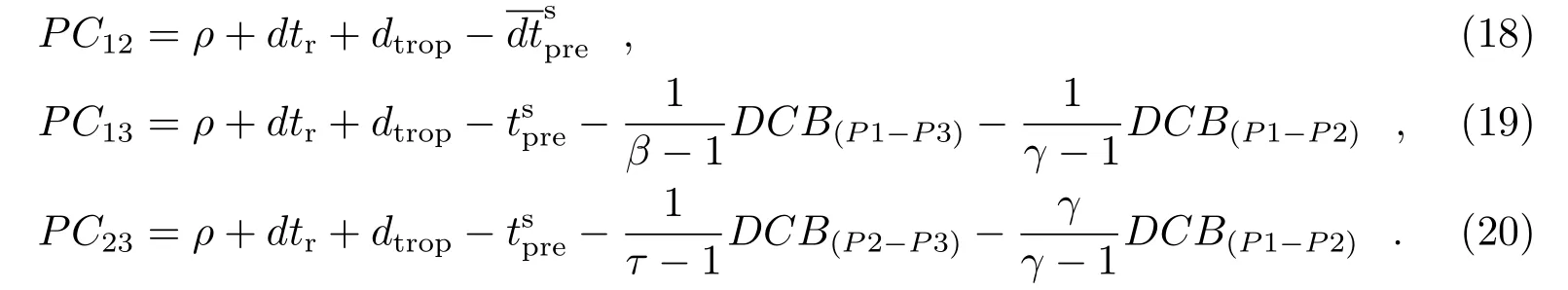
在利用式(15)―(20)进行硬件延迟改正时，如果无法获得北斗的DCB，可以用TGD进行代替，即：

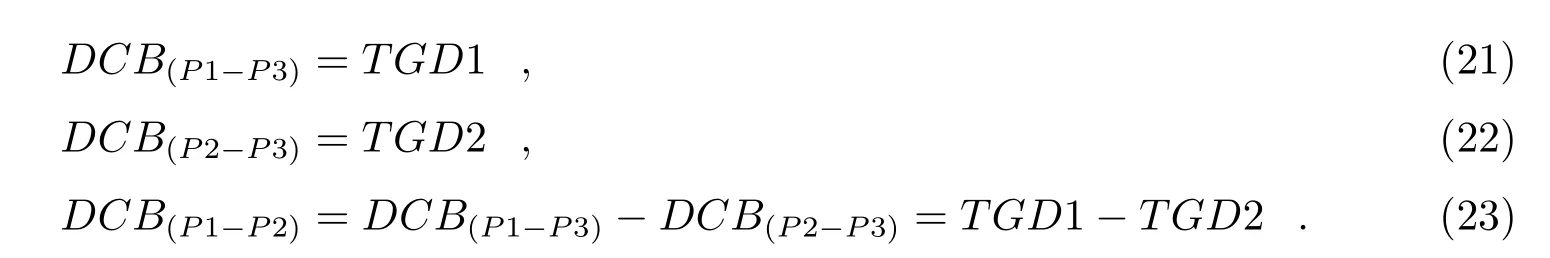
3 BDS-2的TGD参数精度分析

MGEX 提供的北斗DCB参数是对全球200 个测站的观测结果进行计算所得，而北斗广播星历中TGD参数的计算仅考虑了国内测站的观测结果，因此DCB参数的精度一般高于TGD参数，故用DCB参数作为硬件延迟的标准来计算TGD参数的精度。

为了解决DCB解算过程中的秩亏问题，我们假设所有卫星硬件延迟之和为0。TGD参数解算以约束C01 卫星TGD参数的出厂值为约束条件。因此，DCB与TGD的参考基准不同，不能将TGD与DCB直接做差进行比较。为解决这一问题，我们以C01 卫星为基准，将其他卫星的TGD与C01 卫星的TGD做差得相对TGD值，再将DCB与C01的DCB参数做差得相对DCB值，接着将相对TGD值与相对DCB值进行比较，两者差值可反映TGD的精度。

我们选取2017年年积日120―242 天MGEX 采集的BDS-2 卫星导航电文的TGD，并与MGEX 的DCB进行对比，对比结果如图1所示。从图中可以看出，202 天以前，TGD1−DCB1 的值在0～4 ns 之间波动，202 至203 天，TGD1−DCB1 的值发生了一次跳变；203 天以后，各卫星TGD1 至DCB1 的值接近于0。根据图2可知，MGEX 提供的DCB1 并没有发生跳变，所以图1中的跳变主要是TGD1 跳变所致。表1列出各颗卫星TGD1 的跳变前互差序列均值、跳变前标准差、跳变后互差序列均值、跳变后标准差以及各颗卫星TGD1 的跳变大小。从表中可以看出，TGD1 跳变前，互差均值约为2.569 ns，跳变后互差均值约为0.419 ns，跳变大小约为2.15 ns。跳变后，TGD1 精度与GPS 硬件延迟精度接近。北斗系统的TGD会经常更新，但本次TGD1 的跳变值明显大于跳变前后的标准差，该跳变主要是由北斗系统值与TGD解算的接收机不再采用抗多径算法所致。调整后，TGD与MGEX 提供的DCB更接近。

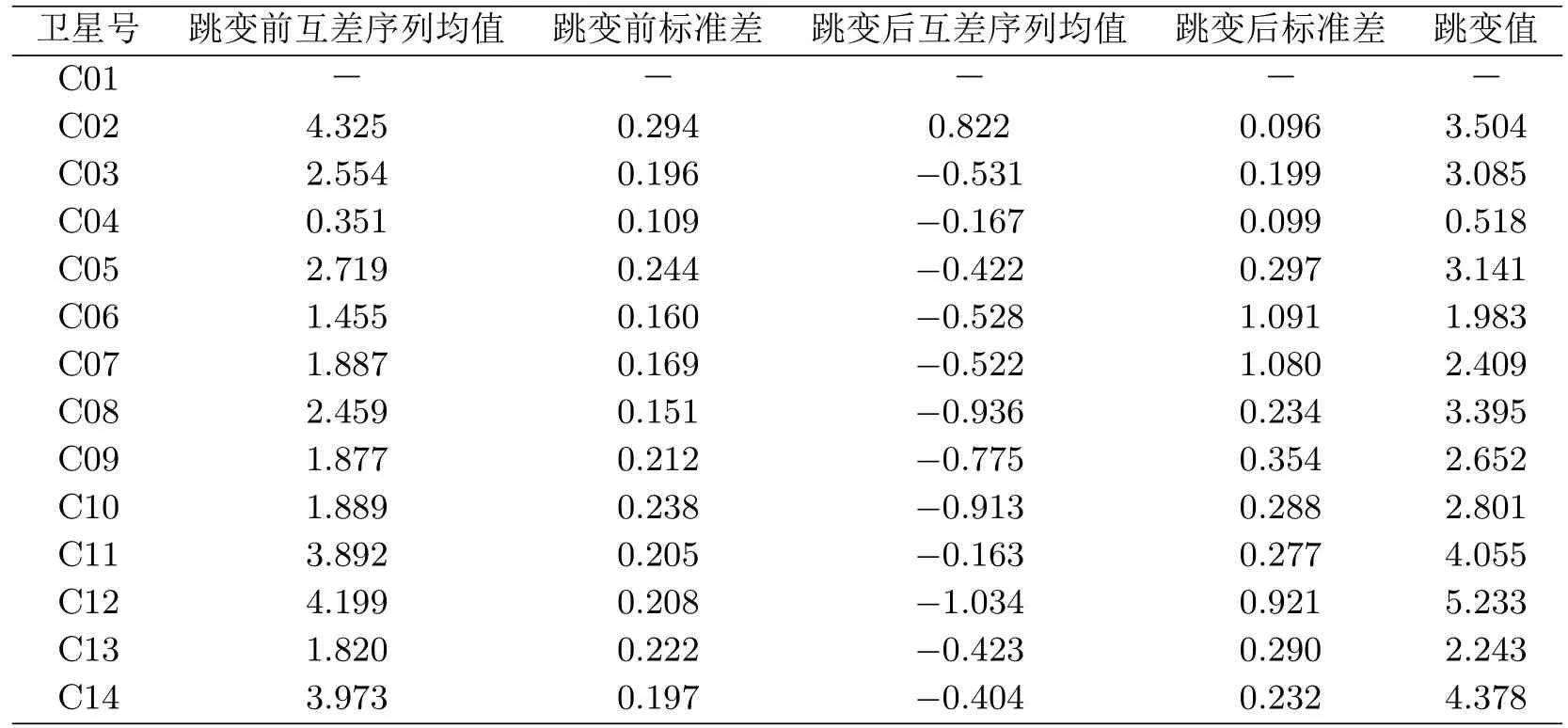
表1 各卫星TGD1 −DCB1 跳变量ns

表2列出各颗卫星TGD2 参数跳变前互差序列均值、跳变前标准差、跳变后互差序列均值、跳变后标准差以及各颗卫星TGD2 参数的跳变大小。对各颗卫星而言，其TGD2−DCB2 的值基本没有发生跳变，其值稳定在0～1.5 ns 之间，其中TGD2−DCB2最大值为1.409 ns，最小值为0.046 ns，平均值为0.565 ns。TGD2 参数精度与GPS 硬件延迟精度比较接近。

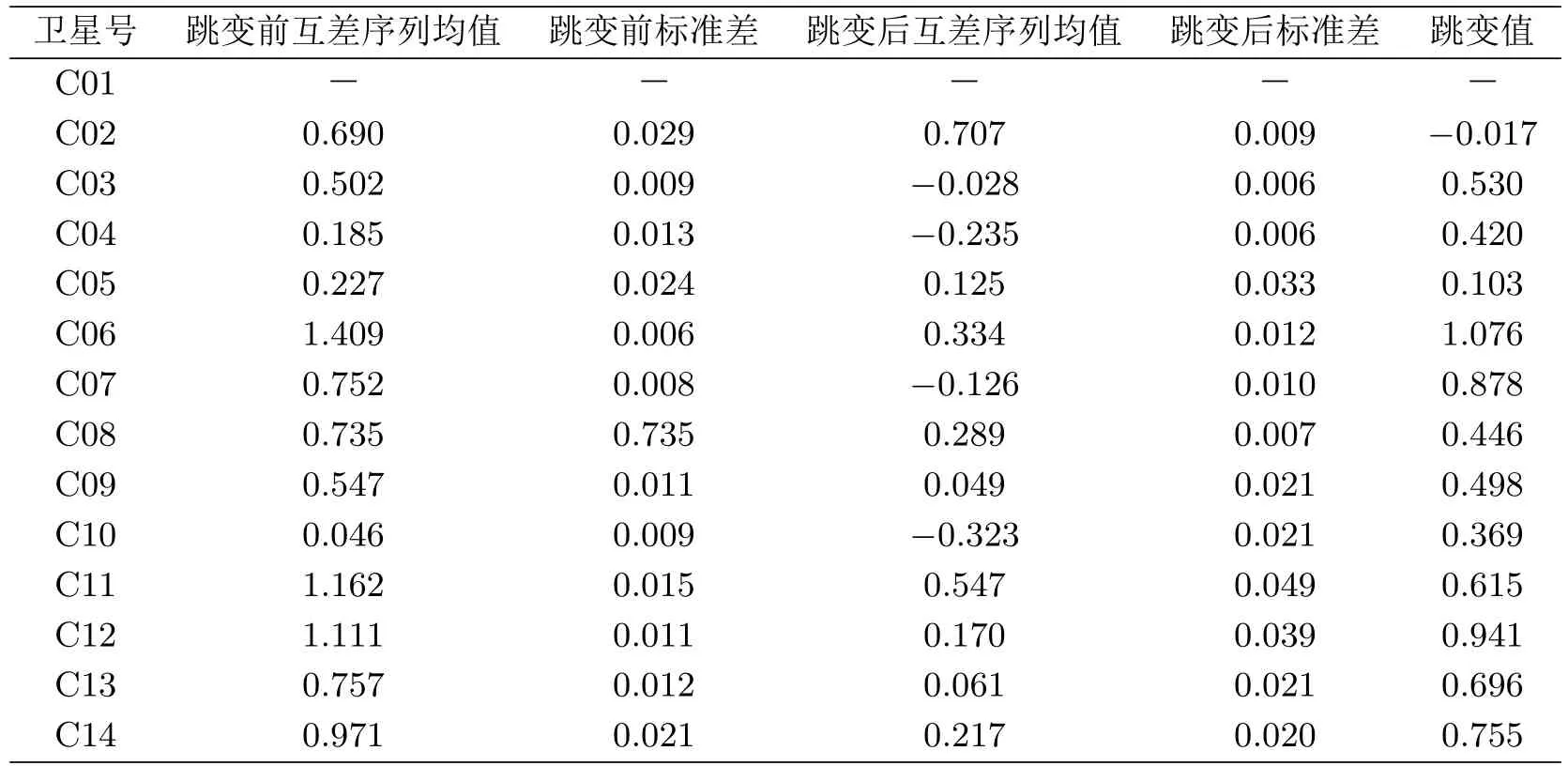
表2 各卫星TGD2 −DCB2 跳变量 ns

4 BDS-2TGD参数对定位结果的影响

表3利用2017年年积日202 天的数据和4 个测站的观测数据，列出了不改正TGD、跳变前改正TGD、跳变后改正TGD以及改正DCB的单点定位结果。

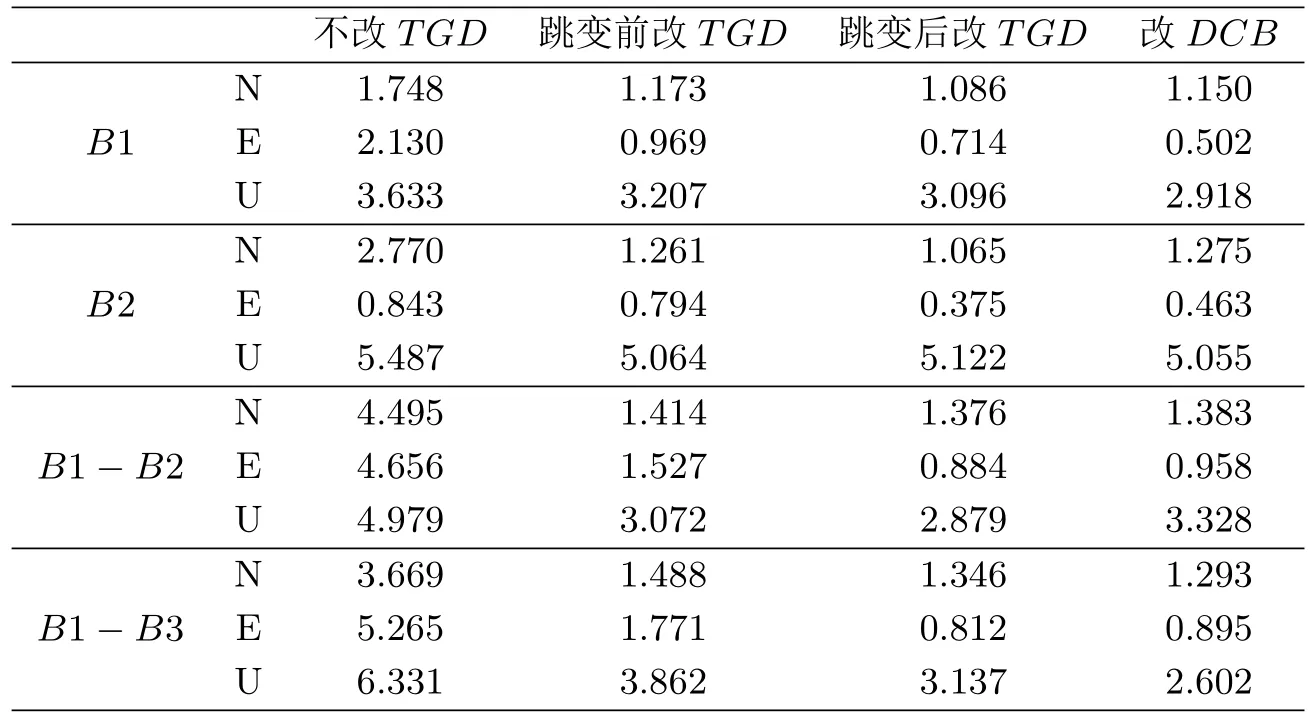
表3 TGD 参数调整前后定位精度的比较 ns

图3 列出了JFNG 测站不改正TGD，跳变前改TGD，跳变后改TGD，以及改正DCB的B1−B2 双频组合的N,E,U 方向定位结果。从图3和表3可以看出，在不利用TGD或DCB参数进行硬件延迟改正的情况下，双频定位精度明显差于单频定位精度，这主要是由于利用双频组合消除电离层影响时，由硬件延迟所引起的伪距变化量被放大所致。经过TGD和DCB参数改正的单点定位精度明显优于没有经过改正的单点定位精度。利用跳变后的TGD参数进行改正，定位精度也优于利用跳变前的TGD参数改正。

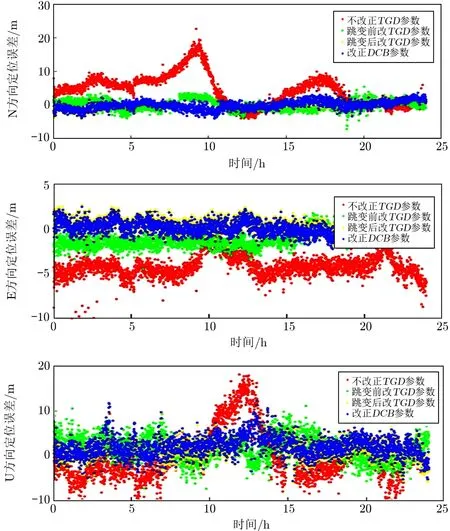
图3 JFNG 测站B1 −B2 双频组合的N,E,U 方向的定位结果

5 结论

本文总结了基于广播星历钟差的TGD/DCB改正模型和基于北斗事后精密钟差的TGD/DCB改正模型。我们利用MGEX 提供的北斗DCB参数计算了广播星历TGD参数的精度，并研究使用TGD和DCB参数对单点定位结果的影响，主要结果如下。

(1)北斗广播星历钟差参数是基于B3 频点计算所得，故使用其他频点单频信号或使用双频无电离层组合时，需要引入TGD或DCB参数进行校正；北斗精密钟差参数是基于B1−B2 频点的无电离层组合计算所得，故使用单频信号或使用其他无电离层组合时，同样需要引入TGD或DCB参数进行校正。

(2)对各颗卫星而言，其TGD2 与DCB2 的差值稳定在0～1 ns 之间。在2017年年积日202 天以前，TGD1 与DCB1 的差值在0～4 ns 间波动；在2017年年积日203 天处，TGD1 参数发生跳变。跳变后，TGD1 与DCB1 之差接近0，故认为跳变后TGD1 参数精度与GPS 硬件延迟精度接近。北斗系统的TGD参数会经常更新，但本次TGD1 参数的跳变大小明显大于跳变前后的标准差，该跳变主要是因参与TGD解算的北斗系统的接收机不再采用抗多径算法所致。调整后，TGD参数与MGEX 提供的DCB参数更接近。

(3)在不使用DCB或TGD改正的情况下，单点定位误差较大；在使用TGD或DCB参数后，单点定位的精度得到了显著提高。利用跳变后的TGD参数进行改正，定位精度也优于利用跳变前TGD参数的改正结果。使用TGD参数定位的结果与使用DCB参数定位的结果比较接近。