电动客车能耗仿真建模与分析

黄炫方， 胡振球， 彭再武， 尹志刚， 樊 钊

(中车时代电动汽车股份有限公司, 湖南 株洲 412007)

能耗指标是电动客车经济性的关键指标之一，能耗的建模与分析有利于降低整车能耗，进而降低车辆的运营成本，具有重要意义。目前能耗的研究主要采用试验对比分析或针对传动参数的经济性分析等形式来评估对能耗的影响，基本停留在部分参数的优化和提升对能耗的影响，未从整体上对车辆能耗进行分析[1-9]。

本文通过理论分析得到电动客车能耗的数学模型，仿真分析系统参数对能耗的影响，提出降低整车能耗的方法，并通过整车进行验证。

1 能耗数学建模

商用电动客车的典型能量传递如图1所示[10]。

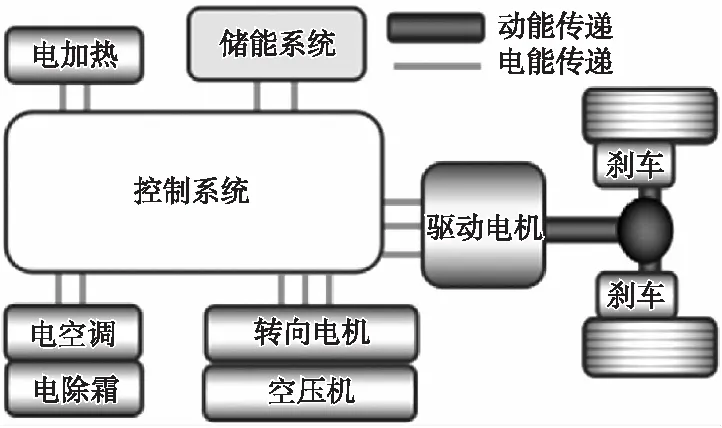
图1 典型能量传递图

根据当前电动商用车实际情况，考虑到后桥反向制动扭矩的限制，假定踩刹车踏板时制动扭矩远大于电机提供的制动扭矩，后桥的最大反向制动扭矩T1小于电机恒转矩区转矩Tm。

下面分别介绍不同部分的能耗：其中R为车辆的轮胎半径;m为整车质量;a为制动减速度;S为行驶距离；Tm为电机恒转矩区转矩;P为电机恒功区功率;nT为电机恒转矩区和恒功区的拐点转速(此时对应的车速为VT)；Fbm为刹车可提供的制动力矩;T1为后桥最大反向制动扭矩;ni为后桥速比。

1.1 机械制动发热能耗ΔE1

根据力学、运动学和能量守恒公式，分别可得[11]:

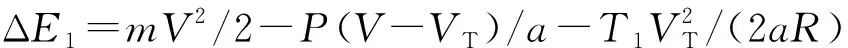
根据电机特性[12]，可以得到：nT=9.55P/Tm。

根据上面公式，推导出机械制动发热能耗ΔE1：

(1)

从式(1)可以看出，后桥的最大反向制动扭矩越大，能耗越小。

1.2 车辆行驶滚阻能耗ΔE2

根据动力学可以得到[13]，

ΔE2=FfS=mgfS

(2)

式中：Ff为汽车滚阻力；f为滚阻系数，可取0.012。

1.3 车辆行驶风阻能耗ΔE3

同理可得：

(3)

式中：A为整车迎风面积；Vmax为车辆的最大车速;CD为风阻系数，取0.65。

式(3)表示风阻能耗为风阻乘以等效线路长度(将行驶距离与车辆速度相乘后除以车辆速度之和，此处等效线路长度为0.651S)。

1.4 辅件能耗ΔE4

ΔE4=KS

(4)

式中：K为电加热或电空调每公里能耗。

1.5 效率能耗ΔE5

效率能耗主要为储能系统、控制系统和驱动系统电能转换的效率损失：

ΔE5=mV2/2(1-0.95)(n1+n2)

(5)

式中：n1和n2分别表示线路的红灯数和站点数。

式(5)表示车辆在站点和红灯处的停车均采用电刹车，其能耗为车辆动能与其效率的乘积。

最终，在行驶里程为S的线路上，车辆的单位里程能耗ΔE为：

ΔE=(ΔE1+ΔE2+ΔE3+ΔE4+ΔE5)/S

(6)

在计算时，部分参数与车型相关，见表1。

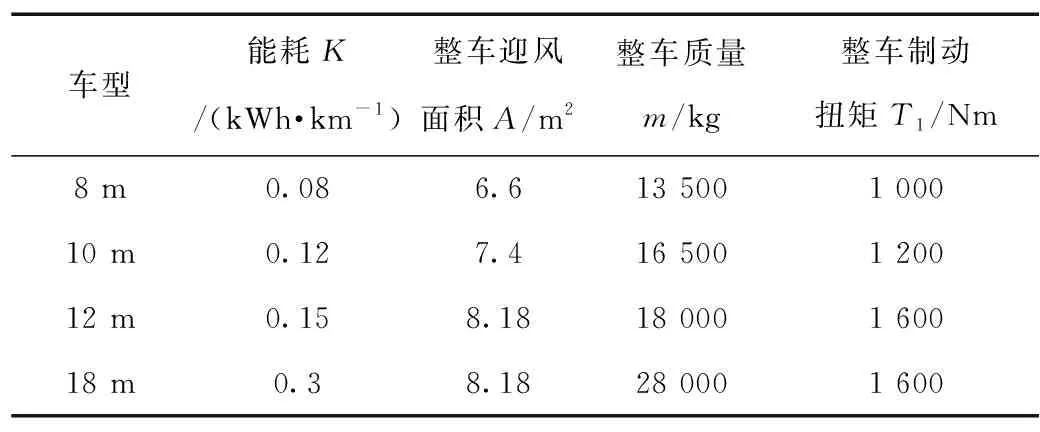
表1 不同车型与参数

为方便分析，部分基础参数取值一致，线路里程S取13.2 km，n1和n2分别取10和20。

2 仿真分析及验证

2.1 仿真分析

根据上述能耗数学模型，使用MATLAB软件进行仿真分析。当Fbm取38 000 Nm,ni取6.2时，图2(a)为R取0.512 m，图2(b)为R取0.385 m的能耗仿真结果。可以看出，在电机扭矩和功率一定的情况下，图2(a)能耗显著高于图2(b)能耗，即随着轮胎半径的增大，能耗增加。

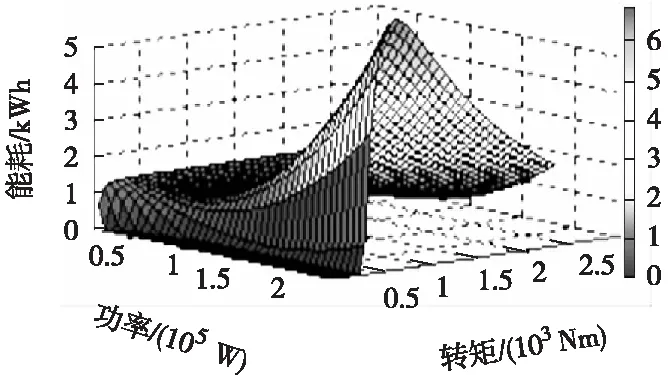
(a) R取值0.512 m

(b) R取值0.385 m

同样，当Fbm和R取值一致，ni取值不一致时，可以得到：随着减速比增加，能耗降低；当ni和R取值一致，Fbm取值不一致时，可以得到：随着刹车制动力矩的增加，能耗增加。在一定范围内，随着电机转矩增加，能耗增加；随着电机功率增加，能耗降低。但由于车辆总的动能一定，当转矩减小或电机功率增加到一定值后，能耗不再降低，甚至有可能增加。

2.2 实验验证

1)为了验证仿真分析的有效性，对不同车型应用上述模型使用MATLAB软件进行仿真计算，并采集不同车型实际运营车辆的能耗数据进行对比，如图3所示。从图中可以看出，根据本文模型，8 m、10 m、12 m、18 m车型仿真计算出的能耗与实际能耗接近。

图3 不同车型实际能耗与仿真能耗对比图

2)为了证明减速系统比直驱系统节能，采集了同车型22辆直驱系统和18辆减速系统相同时间段3个月的运营数据，如图4所示。从图中可以看出，减速系统比直驱系统节能5%～9%。

图4 减速系统与直驱系统能耗对比图

3 结 论

本文通过仿真分析与实验结果，得到以下结论：

1) 减速系统能耗低于直驱系统。

2) 车辆的能耗随着轮胎半径减小、减速比增加、电机转矩减小、电机功率的增加而减小。