例析立体几何中体积问题的解题策略
张得南
(甘肃省永昌县第一高级中学 737200)
一、分割法



例2 如图2,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1和CC1的中点,求四棱锥A1-EBFD1的体积.

点评“分割”的目标是:化陌生问题为熟悉问题,化复杂问题为简单问题,其实质是实现转化.
二、补形法
例3 如图3,在四棱锥P-ABCD中,底面ABCD为平行四边形,侧面三角形PAD的面积为3,点C到平面PAD的距离为1,求四棱锥P-ABCD的体积.
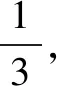

例4 如图4,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,求多面体ABCDE的体积.

点评“补形”的策略是构造熟悉且容易求解的几何体,其本质是一种构造法.
三、转化法
例5 (如图5)在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和CD的中点,求三棱锥F-A1ED1的体积.


例6 如图6,在长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=6,E为CC1的中点,O为下底面正方形的中心,求三棱锥O-A1B1E的体积.

点评这里的“转化”与“变化”,只不过换了一个角度观察,换了一种方法思考,从而达到解决或容易解决问题的目的.例5中把求VF-A1ED1的问题转换为求VD1-A1GE;而例6中把求VO-A1B1E的问题转换为求VA1-MB1E.
四、借助截面
例7 如图7,在斜三棱柱ABC-A1B1C1中,底面是边长为4的正三角形,侧棱AA1=6,并且AA1与 底面两边A1B1、A1C1都成60°角,求三棱锥A-A1B1C1的体积.


例8 如图8,在正四棱柱ABCD-A1B1C1D1中,E是棱DD1上的一点,BD1∥截面EAC,并且截面EAC与底面ABCD所成的角为45°,AB=2,求三棱锥B1-EAC的体积.

点评上面两例,看似与截面无关,但根据题目的特征恰当地做出了相关截面,使复杂问题得到了简化,隐含条件得到了显化,为解题带来了方便.
五、引进变量或选择参数
例9 如图9,在四面体ABCD中,AB=BC=CD=DA=AC=1,求此四面体体积的最大值.


例10 如图10,圆锥的轴截面是等腰直角三角形,母线长为2,P、Q分别是底面圆周上和圆内的动点,且OQ⊥PQ,又E是SP的中点,F是点O在SQ上的射影.
(1)求证:OF⊥平面SPQ;
(2)求三棱锥S-OEF体积的最大值.
解析(1)(解法略)

点评例9与例10都是体积最值问题,通过引进变量或选择参数,建立目标函数,分析函数的结构特点,运用不等式性质和三角函数的有界性来解之,明显来的巧妙、方便.
六、特殊化处理
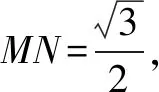


例12如图12,在棱长为2的正方体ABCD-A1B1C1D1中,动点E、F在棱A1B1上,动点P、Q在棱AD,CD上若EF=1,DP=a,求四面体PEFQ的体积.

点评立体几何中的动点问题,貌似让人捉摸不定,不知从何处入手,其实问题的关键是如何分析题设条件,如何在原图基础上化“动”为“静”,化“立体”为“平面”,增添必要的平面辅助图,并合理运用相关知识,如例11中把M定在A1处,例12中把E定在A1处,问题便迎刃而解.

