改进几何法求解逆运动学的仿真和实验研究

王 垚，何秋生，李晓云，卢 冉

(太原科技大学电子信息工程学院，太原 030024)

机器人的逆运动学是研究机器人的基础，深入研究机器人逆运动学，寻求一种准确可靠的逆运动学求解方法可以为后续的轨迹规划减小控制误差，为机器人实时控制缩短执行时间[1]。目前，研究机器人的逆运动学解法的相关文献很多；文献[2]中的伪逆法利用雅克比矩阵分析机器人的逆运动学，该法存在大量的矩阵运算，在寻求最优解时易陷入局部极值；文献[3]采用的数值迭代法因其迭代性质导致求解速度慢，不直观且不易理解；文献[4]采用的旋量法对Paden-Kahan子问题依赖性强；文献[5]根据机器人连杆位型分类求逆解的方法普适性不强。

近年来，国内外许多学者研究用人工神经网络算法、遗传算法等智能算法求逆解；文献[6]提出的RBF神经网络与正交最小二乘法结合的求解方法和文献[7]提出的人工神经网络法提高了控制精度但实时性较差不利于机器人的在线控制，文献[8]提出用遗传算法优化BP神经网络权值和阈值但仍存在早熟、收敛等问题。

几何法因其具有计算误差小和控制精度高的优点，被广泛应用在机器人的在线控制中。本文结合Denso-VP6242机器人的结构特点，采用D-H参数法建立连杆坐标系，通过几何法给出机器人逆运动学的求解过程。

1 D-H参数法建立连杆坐标系

本文选用的是六自由度串联机器人Denso-VP6242，其结构如图1所示。

图1 Denso机器人结构
Fig.1 Structure of Denso robot

采用D-H参数法对Denso机器人建立连杆坐标系。建立连杆坐标系[9]的具体步骤为：(1)设定机器人各关节的初始位型如图1；(2)画出6个关节轴线的延长线，以关节轴线的方向为连杆坐标系zi的方向；(3)若相邻两关节轴平行，以相邻连杆的公垂线和关节轴线的交点作为连杆坐标系的原点，连杆坐标系xi的方向为公垂线的方向；若相邻两关节轴线相交则以轴线交点作为连杆坐标系的原点，连杆坐标系xi的方向为垂直于相交两条关节轴线所在平面的方向；(4)用右手法则确定连杆坐标系yi的方向。Denso机器人的连杆坐标系如图2所示。

图2 Denso机器人的连杆坐标系
Fig.2 Coordinates of Denso robot

其中变量θi表示绕zi轴从xi-1旋转到xi的角度；di表示沿zi轴从xi-1移动到xi的距离；ai表示沿xi轴从zi-1移动到zi的距离；αi表示绕xi轴从zi-1旋转到zi的角度；Pw是腕部参考点，P是机器人末端点，Denso-VP6242机器人的D-H参数如表1所示。

表1 Denso机器人的连杆参数
Tab.1 Parameters of Denso robot

连杆iθi/(rad)αi/(rad)ai/(m)di/(m)变量范围/(rad)1θ1π/200.125-2.7925,2.79252θ200.2100-2.0944,2.09443θ3-π/2-0.0750-2.7925,0.33164θ4π/200.210-2.7925,2.79255θ5-π/200-2.0944,2.09446θ6000.070-6.2832,6.2832

2 传统几何法求解关节角θ1，θ2和θ3

逆运动学是实现机器人路径规划、实时控制的基础，研究一种简单高效的逆运动学解法具有重要的意义。根据机器人末端位姿矩阵T6求解机器人各个关节对应的角度值q，对应关系可表示为：

q=Denso_IPK(T6)

(1)

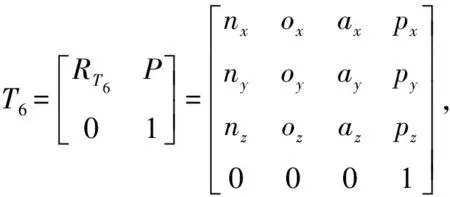
根据六自由度串联机器人Denso-VP6242的几何结构计算与位置相关的关节角度θ1，θ2和θ3的具体步骤如下：

(1)根据机器人末端在笛卡尔空间中的位置P的坐标和机器人末端的接近矢量a求解腕部参考点Pw的位置坐标，表达式为：

Pw=[x,y,z]=[px,py,pz]-d6·[ax,ay,az]

(2)

(2)机器人在xoy平面上的投影如图3所示，图中pw为腕部参考点Pw在xoy平面上的投影。

图3 机器人在xoy平面的投影
Fig.3 Robot’s projection onxoy

由此可得：θ1=arctan2(y,x)

(3)

根据式(3)和x，y的符号可在关节变量范围内求出唯一的θ1.

从图4中应用平面几何关系可以得出关节角θ3的表达式为：

θ3=α1+α2

(4)

图4 机器人在zop平面的投影
Fig.4 Robot’s projection on zop

同理可得关节角θ2的表达式为：

θ2=β1-β2

(5)

β2=β3=atctan2(l,c)；

3 改进几何法求解关节角θ4，θ5和θ6

由于传统几何法通过分离变换矩阵中的变量推算关节角度，计算过程中矩阵运算量大、存在误差，求解非常困难[10-11]。因此考虑研究一种改进几何法，简化求解过程，达到提高控制精度的目的。

改进几何法求解关节角θ4，θ5和θ6的思路为：首先根据给定的机器人姿态转换为RPY组合表示的姿态角，然后由姿态角和六自由度机器人关节角的关系求解θ4，θ5和θ6.

RPY组合即用横滚(roll)、俯仰(pitch)和偏转(yaw)组合变换表示机器人末端姿态，其中横滚(roll)角γ表示机器人末端相对于基坐标系的z轴旋转γ角，俯仰(pitch)角β表示机器人末端相对于基坐标系的y轴旋转β角，偏转(yaw)角为α表示机器人末端相对于基坐标系的x轴旋转为α角，如图5所示。

图5 RPY组合变换表示姿态
Fig.5 RPY showing posture

当已知机器人的位姿矩阵时，可通过旋转矩阵RT6与RPY组合表示的姿态角关系表达式(6)求解偏转角α，俯仰角β，横滚角γ，表达式为：

PRY(γ,β,α)=

(6)

式(6)中：cα=cos(α)，sα=sin(α)

当机器人末端相对于基坐标系的偏转角α，俯仰角β，横滚角γ已知时，根据机器人的六个关节角与末端姿态角的关系：

(7)

由此可求得机器人的关节角θ4，θ5和θ6.

在求逆过程中，出现一个关节角对应多种解法的情况，但在实际控制过程中不允许出现多解情况，本文以路径最短为优选策略选取一组最优解。设定优选目标函数为：

(8)

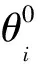
求解各个关节角最优解的算法流程如图6所示。

4 仿真和实验验证

图6 最优解算法流程图
Fig.6 Algorithm flow chart of optimal solution

设定机器人姿态始终为[α，β，γ]=[0，-pi，0]，机器人末端位置取圆弧曲线上的点，圆弧曲线表达式为式(9):

(9)

图7 机器人仿真模型
Fig.7 The simulink modle of robot

圆弧曲线和期望末端位置采样点如图8所示。

当k=0:π/20:2π时，可得期望末端位置点的坐标p=x(k),y(k),z(k)，然后求解逆运动学得相应的关节角度。通过对比传统几何法和改进几何法的位置误差和姿态误差，验证改进几何法的优越性，其中姿态误差为实际旋转矩阵与期望旋转矩阵所有元素的绝对误差。

图8 目标圆弧曲线及采样点
Fig.8 Task trajectory and sample points

采用传统的几何法求得位置误差为:

(10)

式(10)中：[x1,y1,z1]为采用传统的几何法求得实际末端位置坐标。

同理，采用改进的几何法求得实际末端位置坐标为p2=[x2,y2,z2]时位置误差为：

(11)

式(11)中：[x2,y2,z2]为采用改进的几何法求得实际末端位置坐标。仿真结果如图9所示。

图9 传统几何法和改进几何法的位置误差
Fig.9 Position error of traditional and advanced Geometr

采用传统几何法的姿态误差er1和采用改进几何法的姿态误差er2仿真结果如图10所示。

仿真结果看出：与传统几何法相比，采用改进几何法位置误差和姿态误差小，求解精度高，验证了本文研究的改进几何法的优越性。

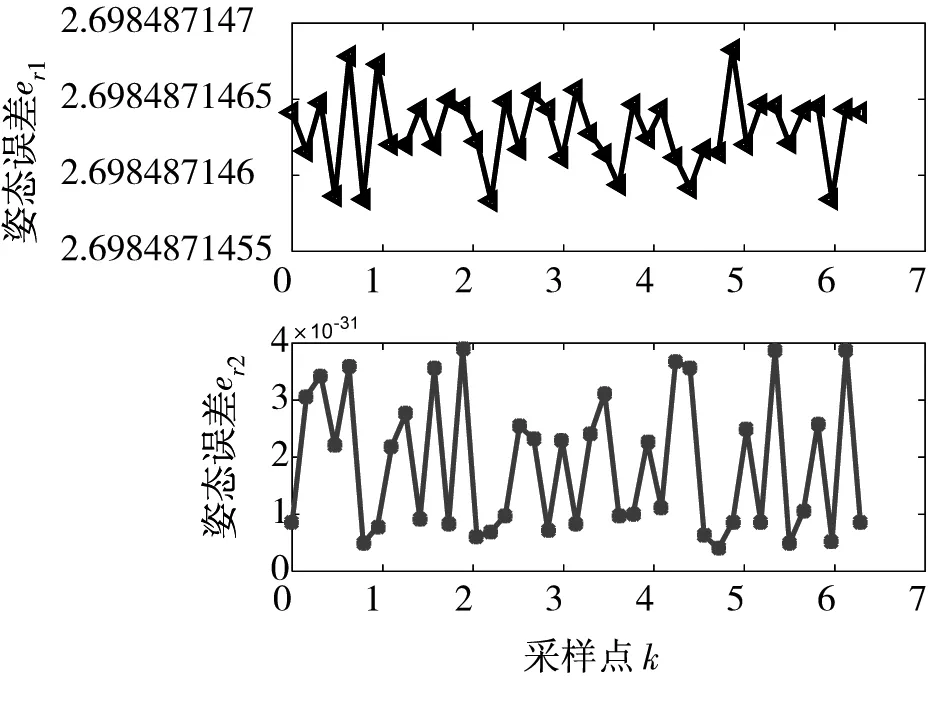
图10 传统几何法和改进几何法的姿态误差
Fig.10 Posture error of traditional and advanced Geometry

在实验室现有的六自由度机器人Denso-VP6242控制平台上进行实验，验证本文研究的改进几何法在实时机器人控制平台中的可行性。以绘制圆弧为例，分别采用传统几何法和改进几何法控制机器人，并将机器人画出的圆弧进行比较，图11是实验结果。

图11(a)为期望圆弧曲线，(b)为采用传统几何法控制机器人画出的圆弧曲线，(c)为采用改进几何法控制机器人画出的圆弧曲线，目标圆弧是直径为0.05 m的圆，图11中图(c)比(b)的直径更接近0.05 m，曲线更为光滑。实验结果验证了该方法的可行性和优越性。

5 结 论

(1)研究了一种改进几何法。借助robotics toolbox进行逆运动学仿真，结果表明该方法可以减小机器人位姿误差，提高控制精度。其中，位置误差在10-16数量级，姿态误差在10-31数量级。

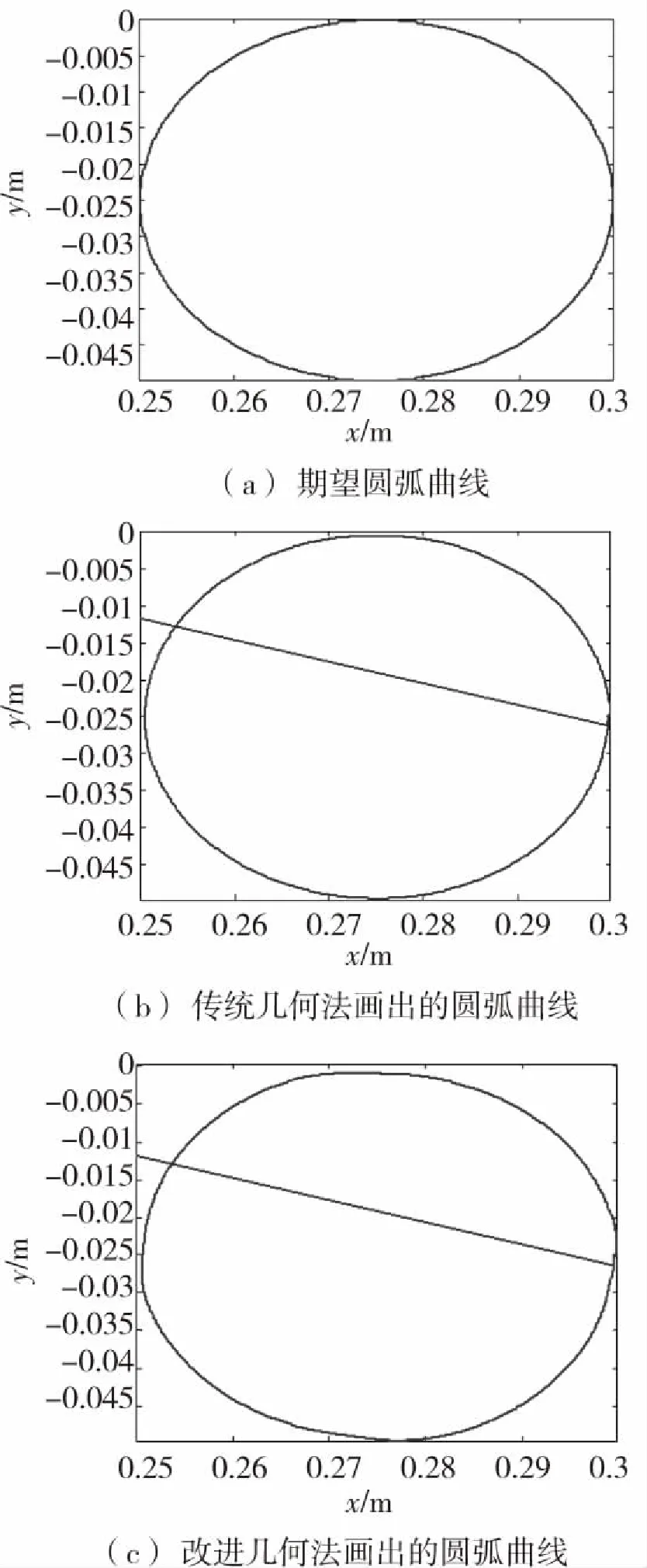
图11 实验结果
Fig.11Theexperimentalresults

(2)将改进几何法应用到实际机器人控制平台中，实验结果表明改进几何法的可靠性和优越性，为研究机器人轨迹规划和实时控制奠定了基础。