大型LNG运输船结构疲劳损伤分析方法

(中海油能源发展股份有限公司 采油服务分公司，天津 300452)

由于海洋环境载荷的交变作用，疲劳破坏是船舶结构破坏的最主要形式之一[1]。已有研究表明，船体疲劳裂纹经常出现在尖舱区域、船舯部甲板与船底区域、桥楼两端的舷墙及甲板大开口处[2]，船长超过200 m的大型船舶，其总损伤的70%以上都属于疲劳裂纹[3]。目前新建造的LNG运输船疲劳寿命要求一般为40年，而且要求无限航区。一旦发生结构疲劳损伤将给LNG运输带来较大隐患；船舶发生计划外的坞修除了产生高额的坞修费用之外还会带来数百万甚至超过千万美元的租金损失。因此从安全和经济的角度考虑，在设计阶段对LNG运输船进行疲劳分析就显得尤为重要。

本文结合目前使用较为广泛的疲劳校核方法，选择谱疲劳分析法进行实际验算，对船级社规定进行疲劳分析的节点进行总结对容易发生疲劳损伤的位置提出补强建议。

1 疲劳强度的校核方法

目前常用的疲劳强度校核方法包括基于线性累计损伤理论的S-N曲线法和基于Paris裂纹发展理论的断裂力学方法。S-N曲线法更适合工程应用，分为简化分析方法和谱分析法。

简化分析法使用简化的船舶载荷和简化的结构应力响应，计算较为简便，各大船级社均有自己提出的简化分析方法。

但是有报告指出按照各船级社的简化分析法进行某集装箱船舱口围板疲劳分析时，得出的结果差异很大，预测的疲劳寿命从1.8年到20.7年不等[4]。主要原因是船舶载荷和结构应力响应是进行疲劳分析的核心因素，基于大量经验总结和统计资料反馈的简单的公式或者参数值难以满足不断出现的新船型的要求。

谱分析法考虑的因素包括航区海况、多种船舶装载工况等，主要假设短期海况符合平稳的正态分布，以此来通过波浪的统计特性得出船舶结构受到的交变应力，较为贴近现实情况。本文尝试使用谱分析法进行ABS规定的部分高应力节点疲劳强度校核。

1.1 谱疲劳分析法的主要假定及公式推导过程

海面波动形成海浪，而海浪是一个随机变化的过程，浪高、波动周期都是不断变化的。为了尽可能模拟真实的海况并方便计算，将一个固定点的海浪分解成多个简单的随机余弦波的叠加[5]。

(1)

式中:An为第n个余弦组成波的振幅；wn为第n个余弦组成波的圆频率；εn为第n个余弦组成波的随机初相位角，均匀分布在0～2π的范围内。

当尝试计算一定频率范围内(ω～ω+Δω)的波浪能量时采用下面的函数。

(2)

S(ω)相当于能量密度相对于组成波频率的分布函数，称其为能谱或者波浪频谱。

使用海况散点图表示波浪在以年为单位的时间段内的表现并以此为依据预测船舶整个寿命周期内受到的波浪动载荷。显然，某些年份的海况会比此处海况散点图显示的更加恶劣，某些年份的海况又会比参考值温和一些，船舶整个生命周期内除去海上航行还有港口停泊、设备维护、坞修等活动，因此整体考虑认为并不会受到比计算值更大的波浪载荷。北大西洋海况散点图见表1。

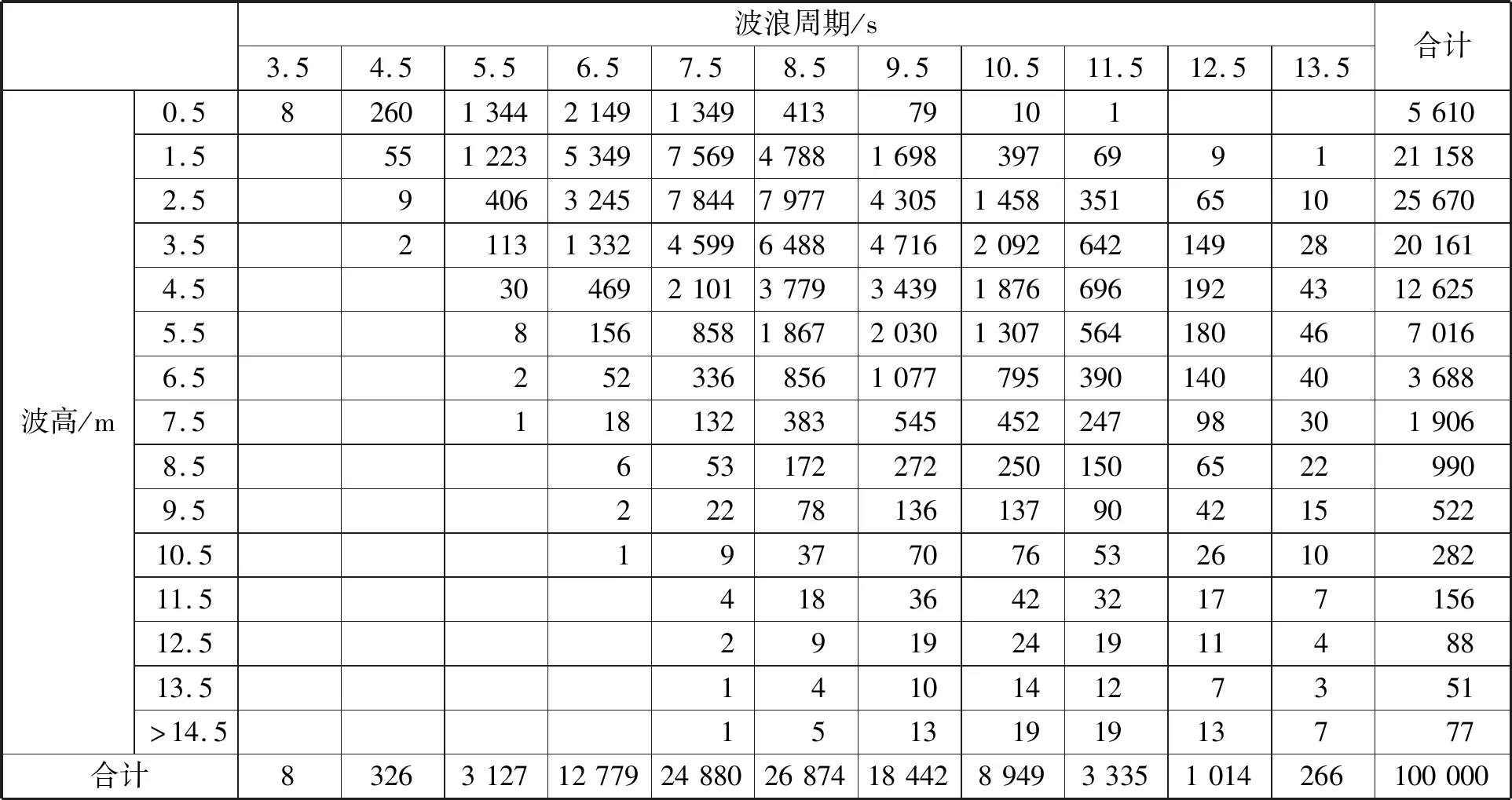
表1 北大西洋海况散点图

在表1中，每一个单元格中的数字表示某个特定周期和波高的波在100 000个被记录的海况中出现的次数。

1.2 波浪能量谱

假设某短期海况下的波浪能量谱为Sη(ω)，则长期海况下的波浪能量E即可表示为

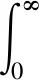
(3)

当考虑浪向角的影响时，上式可完善为

Sη(ω∣HS,TZ,θ)=Sη(ω∣HS,TZ)·F(θ)

(4)

Sη(ω|HS,TZ)在这里表示短期海况下的点谱能量，θ表示浪向角，F(θ)表示对应的方向函数。

常用的布雷特施奈德点谱如下。

(5)

方向函数如下。

(6)

1.3 结构响应的频域分析

短期海况下的复杂波可以被近似分解为有限个规则波，引起疲劳裂纹的交变应力可由波浪能量谱来获得，计算波浪能量谱的参数包括短期海况(Hs，Tz)，船舶浪向角(θ)，航速(V)和装载状态(L)。

Sσ(ω|HS,TZ,V,L,θ)=

|H(ω|V,L,θ)|2·Sη(ω|θ)

(7)

1.4 疲劳损伤分析

短期海况下导致疲劳损伤的应力范围通常由波浪散点图中各单元对应的概率密度函数得出，通过谱分析法推导出概率密度函数。为了将浪涌的影响加以考虑，采用雨流法对计算结果加以修正。在求得短期海况下的疲劳损伤后，通过加权求和法得到长期海况下的疲劳损伤。

求解海洋结构物疲劳强度谱分析法的基本步骤如下。

1)计算疲劳应力传递函数。

使用直接计算法来确定疲劳节点在不同装载状态、波浪频率、浪向角影响下的应力响应并以此来确定应力传递系数Hσ(ω│θ)。

通过波浪能谱Sη(ω│HS,TZ)和应力传递系数来计算应力能谱Sσ(ω│HS,TZ,θ)，其中HS表示有义波高，TZ表示平均跨零周期。

Sσ(ω│HS,TZ,θ)=

│Hσ(ω│θ)│2·Sη(ω│HS,TZ)

(8)

2)计算谱矩。

第n阶谱矩mn的表达式为

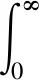
(9)

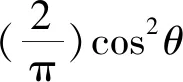
ωnSσ(ω│HS,TZ,θ)dω

(10)

使用瑞利(Rayleigh)分布下的概率密度函数来表示各短期海况的应力响应，应力响应的跨零周期和带宽公式如下。

瑞利分布下的概率密度函数为

(11)

跨零周期为

(12)

带宽为

(13)

S表示应力范围，等于应力幅值的2倍。σ=m0。m0、m2、m4分别为0阶谱矩，2阶谱矩和4阶谱矩。

基于线性累积损伤理论计算各短期海况下的疲劳损伤di的累计值D为

(14)

式中：ni为某一应力范围内的应力循环次数，Ni为根据S-N曲线在该应力范围下恒幅交变应力导致结构发生疲劳损伤需要的应力循环次数，J为应力范围的数量。当D大于1时，结构就会发生疲劳损伤。

假定S-N曲线符合N=AS-M的形式，那么在第i个海况下发生的短期疲劳损伤如下。

(15)

式中：Di为表示第i个海况中产生的疲劳损伤；kh为钢材参数。当材料为低碳钢时kh=1；当材料型号为H32时kh=0.962；材料型号为H36时kh=0.885；材料型号为H40时kh=0.87。

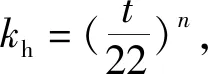
当板厚小于22 mm时，kt=1。

累积疲劳损伤值D为

(16)

对于双直线S-N曲线，结构的总体疲劳损伤可以表示为

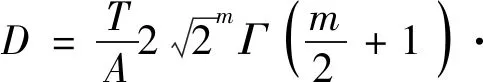
(17)

式中：μi表示S-N曲线下半段的疲劳贡献因子，当短期海况应力范围符合瑞利分布时，

μi=1-

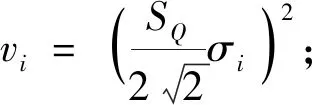
2 疲劳分析位置选择和计算结果

从结构发生突变和受到频繁的交变应力两方面考虑，选择上斜旁与甲板连接处大肘板的趾端进行疲劳寿命校核，计算结果表明，与船艏部甲板连接处的趾端疲劳寿命均大于500年，满足设计疲劳寿命。

与船艉部居住舱室处甲板连接处趾端疲劳寿命分别为290年和85年，满足设计疲劳寿命。

3 LNG船疲劳寿命校核时节点位置选择原则

ABS对于LNG运输船疲劳寿命校核的节点选择如下。

上斜旁板与货舱穹顶内甲板的连接处；上斜旁板与货舱内纵壁的连接处，见图1。

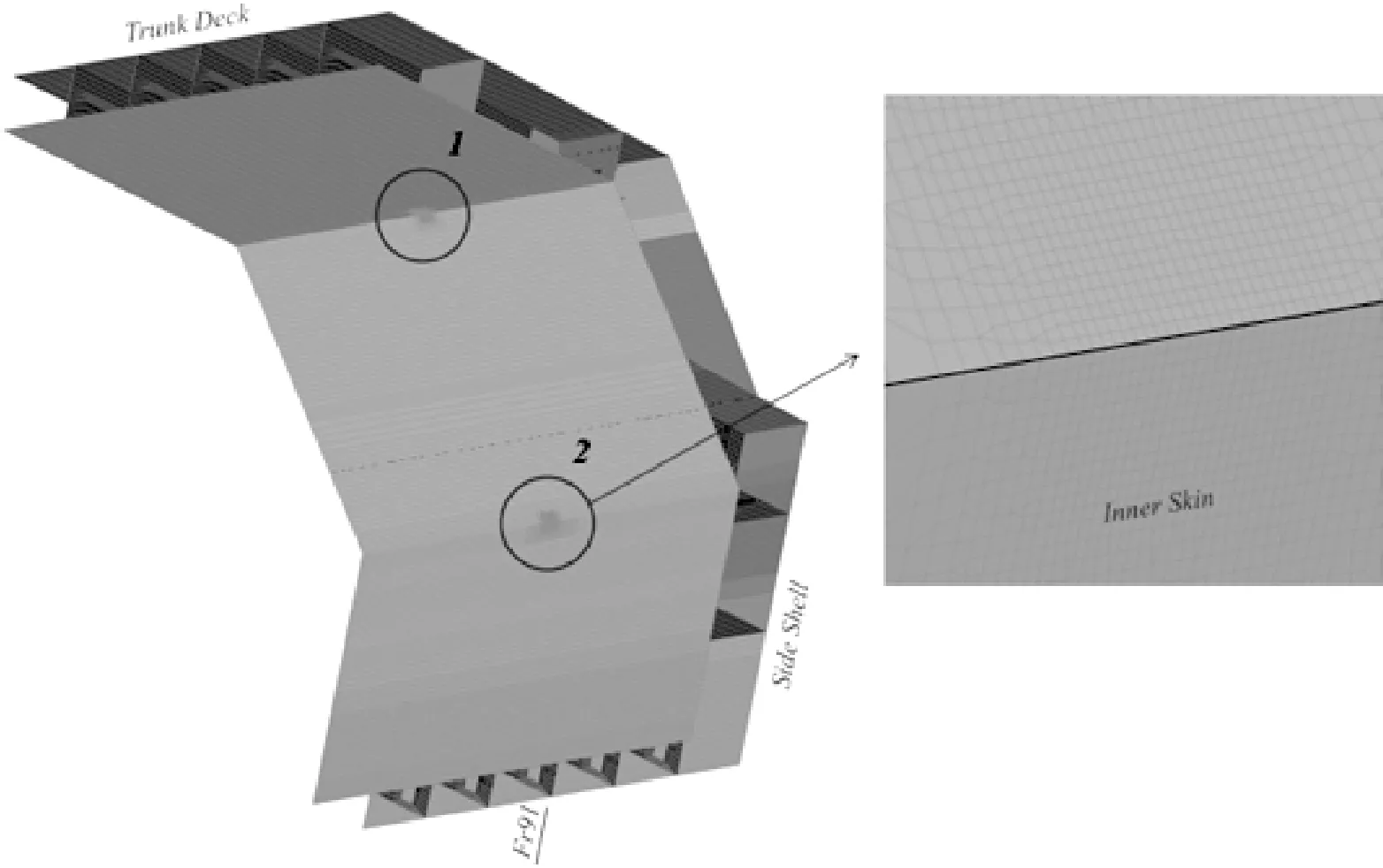
图1 上斜旁舱壁附近疲劳寿命校核点

下斜旁板与货舱内底板的连接处；下斜旁板与货舱内纵壁的连接处，见图2。

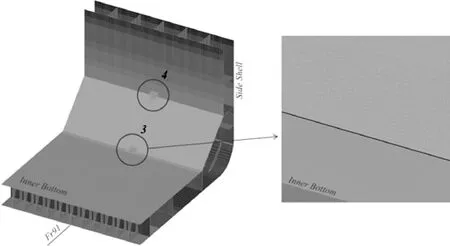
图2 上斜旁舱壁附近疲劳寿命校核点

边压载舱内纵向骨材与横向肋板连接处，见图3。

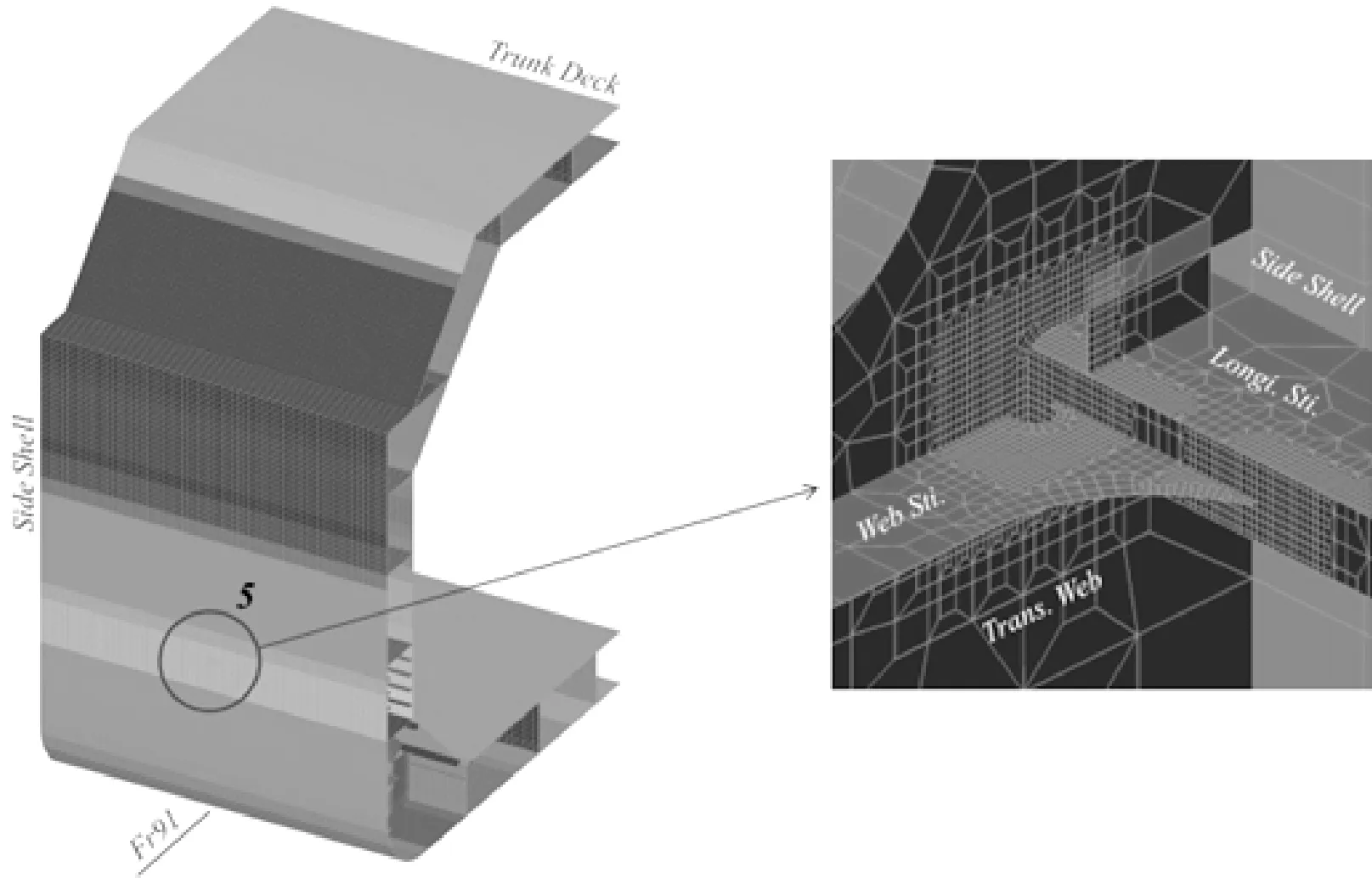
图3 底边舱纵向骨材与横向构件连接处疲劳寿命校核点

双层底纵桁与横隔舱舱壁连接处，见图4。

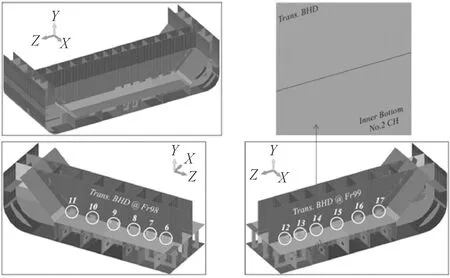
图4 三向构件结合处疲劳寿命校核点

边压载舱纵向桁材与横隔舱连接处，见图5。

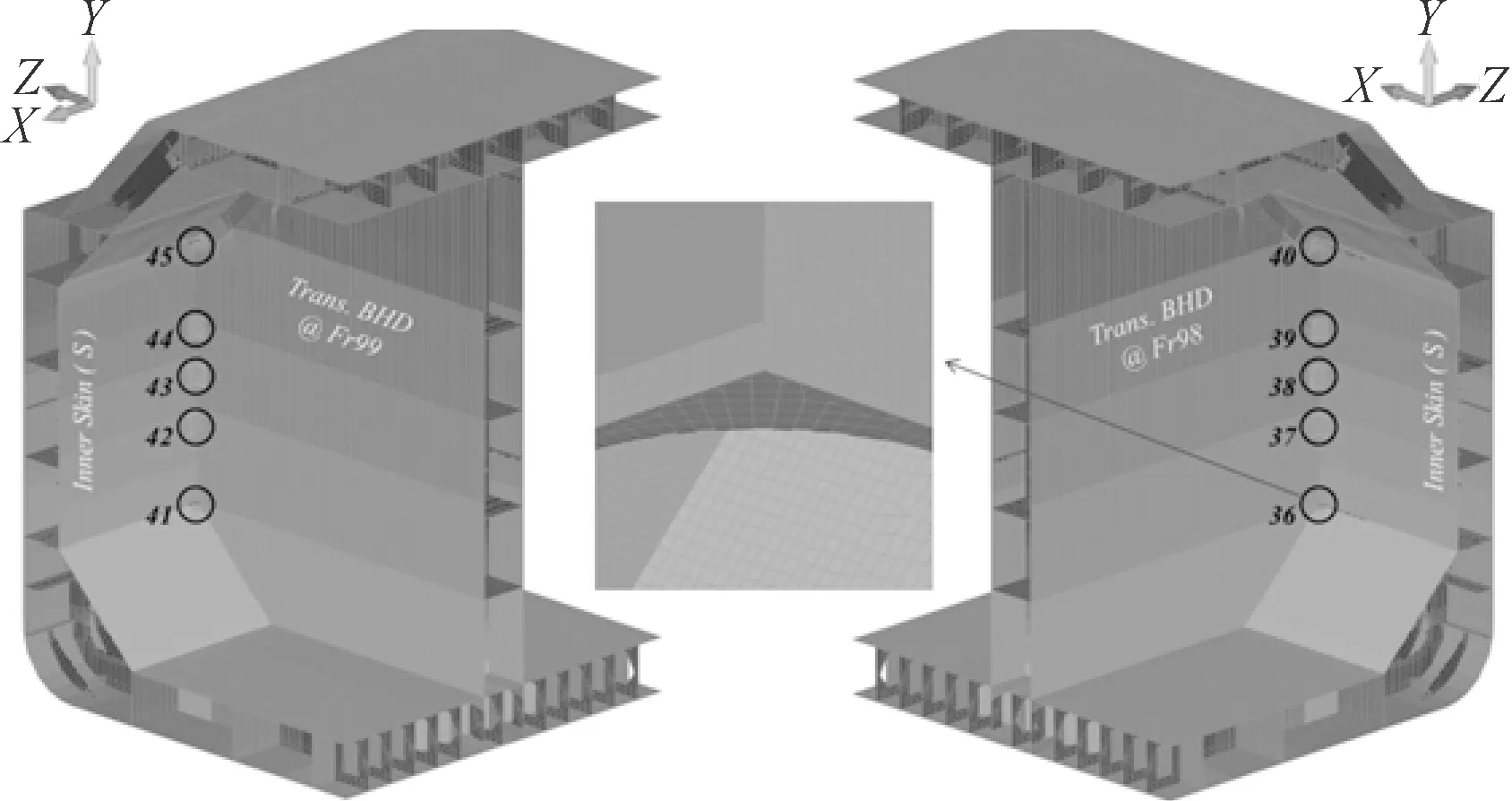
图5 三向构件结合处疲劳寿命校核点

穹顶大开口，见图6。

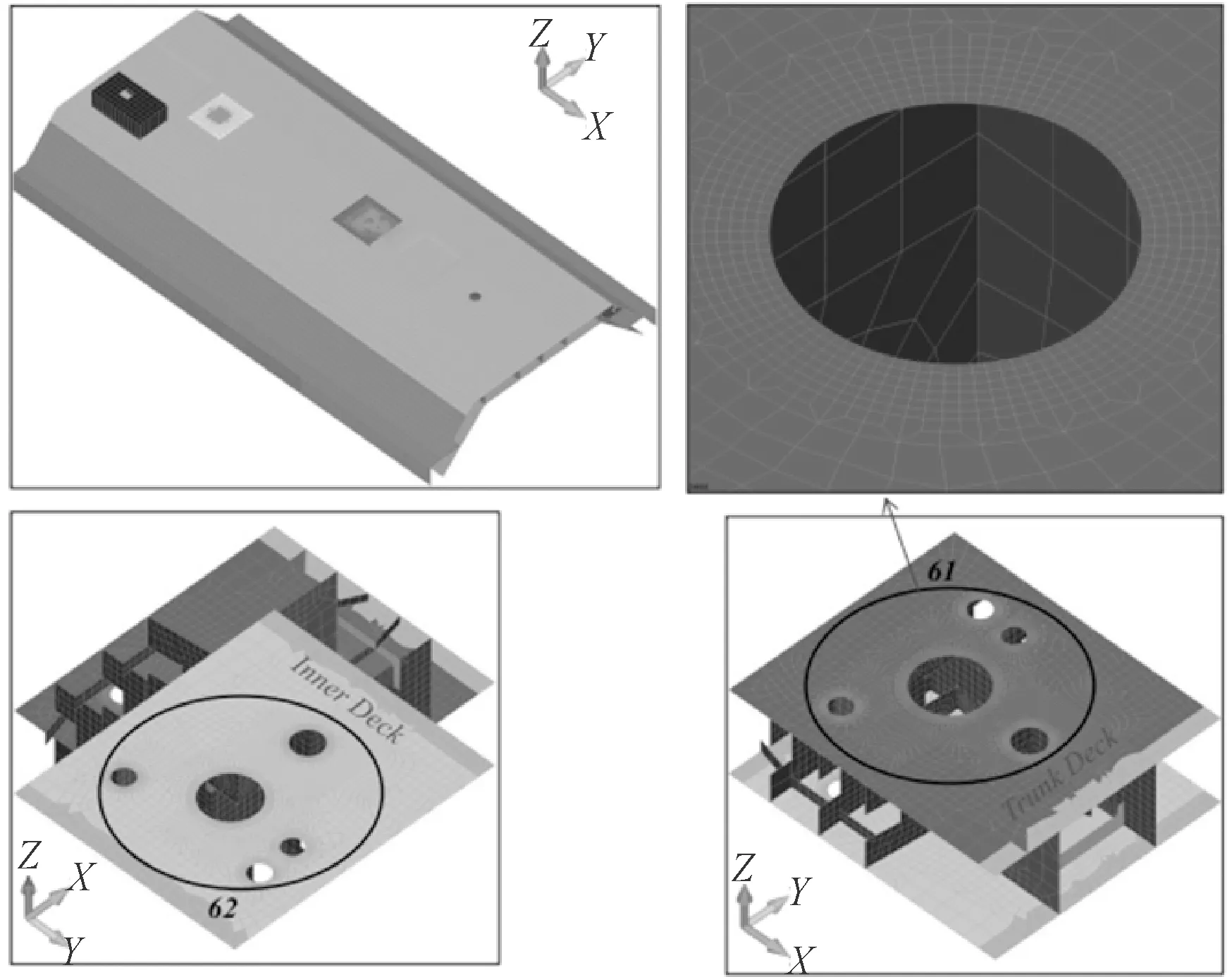
图6 大开口处疲劳寿命校核点

上斜旁板尽头与上建连接处及船艏部连接处的大肘板，见图7。

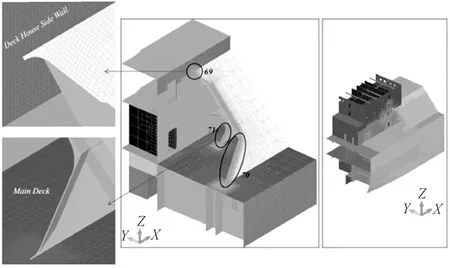
图7 结构突变处疲劳寿命校核点

船中位置甲板上小的甲板室开口以及甲板室围壁与甲板的连接处，见图8。

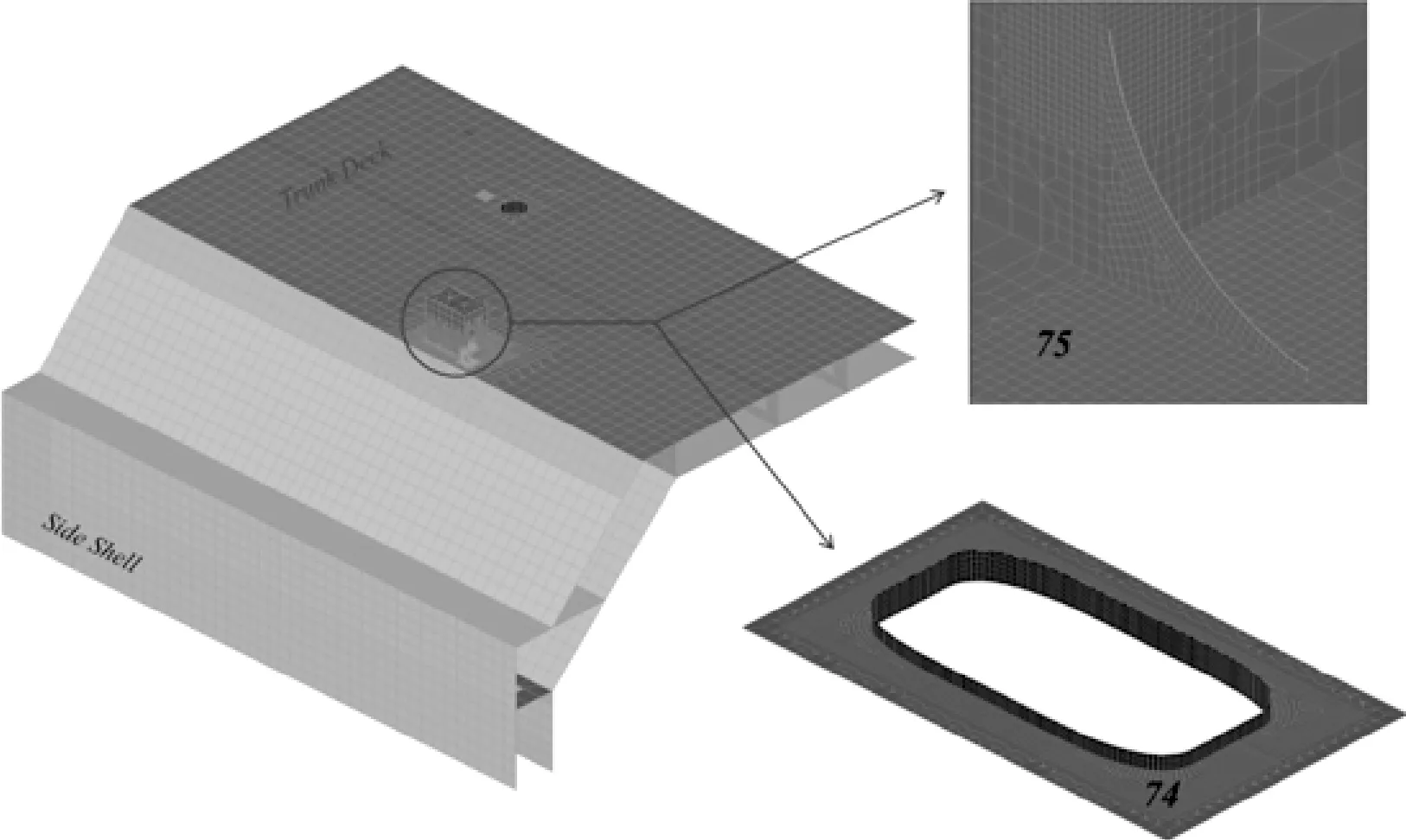
图8 小型甲板室与甲板连接处疲劳寿命校核点

货物机械室端头与甲板连接处，见图9。

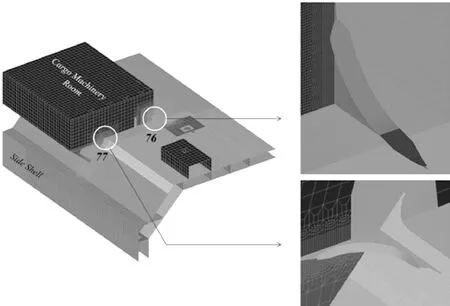
图9 大型甲板室与甲板连接处疲劳寿命校核点

位置选择的主要特点包括：主要结构发生突变处如上斜旁板与甲板的连接处、各种折角的位置、受力条件复杂的位置如纵向强结构与横舱壁以及内底板连接处，纵向强结构与横舱壁及内纵壁连接处等，当3个强力构件相交时就需要留意该处的疲劳强度问题。甲板大开口处如液穹、气穹开口处，电缆通道。

在实船建造过程中，上述区域的结构板厚及材料等级与相邻部位相比有所增加。对于3个强力构件相交的位置，还特别提出了关于角焊缝的光顺打磨要求。常规光顺打磨仅做到表面光顺，并不能真正起到延长疲劳寿命的作用，需要做到角焊缝剖面与相邻的舱壁光顺过渡才能达到抗疲劳的目的。

4 结论

经过计算，原设计在上斜旁与甲板连接处过渡肘板趾端的疲劳强度是足够的。

疲劳强度与屈服强度之间存在一定的关系，易发生疲劳损伤的节点位置与高应力节点位置之间也存在一定的关系。在疲劳分析之前应通过全船有限元分析找出高应力点或应力集中点的位置，对划定的疲劳分析点位进行补充。

对于易发生疲劳损伤的位置可以通过加大板厚，焊缝处进行光顺打磨，增加肘板，适当延长趾端等方式增加节点弹性，延长疲劳寿命。

关于焊缝处光顺打磨延长疲劳寿命的做法是有效果的，但是针对不同板厚、不同焊角尺寸，如何堆焊打磨才能形成最好的效果，目前还没有形成普遍共识。相信在不久的将来能够出现一个被普遍接受的标准，以便更好地对现场施工及检验进行指导。