基于MATLAB的UR10机器人运动学分析与仿真
马国庆,刘 丽,于正林,曹国华,陈李博
MA Guo-qing, LIU Li, YU Zheng-lin, CAO Guo-hua, CHEN Li-bo
(长春理工大学 机电学院,长春 130022)
0 引言
随着现代工业向智能化与自动化发展,机器人逐渐融入社会各个领域,而机器人的运动学分析是机器人技术研究中的关键环节[1]。本文以UR10为实验平台,对机器人各关节与各连杆进行分析并得到相关的模型参数,并将其应用于正逆运动学求解。用MATLAB进行运动学仿真,通过数据对比分析验证模型与运动学正逆运算的正确性。为机器人轨迹规划研究提供必要的理论基础。
1 机器人模型的空间描述与变换关系
要使机器人实现空间中某种运动,首先需要建立一个基坐标系,然后在此基坐标系下研究机器人的相关参数和位姿。
1.1 机器人位姿及坐标系描述
在建立了基坐标系后,可通过3×1的位置矢量表示空间中某一点的位置。假设基坐标系{A}中任意一点p,其位置矢量可用Ap表示:

其中px,py,pz为p点在基坐标系{A}中的位置分量。但对机器人进行研究时不仅需要该点的位置坐标,还需要方位姿态。因此定义某一物体所在的坐标系为{B},则物体B相对于坐标系{A}的方位可用B的单位矢量相对于坐标系{A}的方向余弦矩阵表示,具体如下:
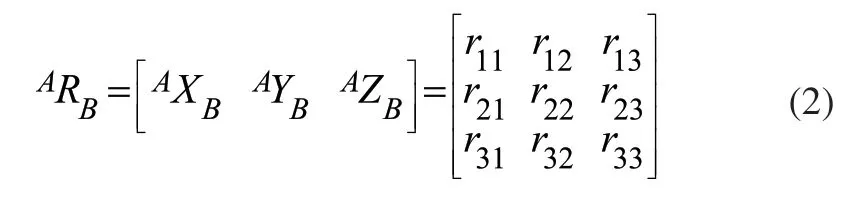
其中ABR称为旋转矩阵,上下标A、B分别表示坐标系{A}与{B}。由于三个列矢量均为单位矢量且均互相垂直,因此为正交矩阵且满足:

1.2 机器人坐标系的变换关系
在空间坐标系转换中最为常见的为平移、旋转以及既平移又旋转的复合变换三种[2]。空间点p在空间坐标系{A}、坐标系{B}和坐标系{C}下的变换关系如图1所示。

图1 位姿变换示意图
坐标系{A}与坐标系{B}在空间中相互平行但坐标原点位置不同。可以把它看成是坐标系的平移变换,用位移矢量ApB表示坐标系{B}相对于坐标系{A}的变换关系,通过矢量加运算即可求解出空间点p相对于坐标系{A}的位置矢量:

坐标系{C}与坐标系{B}在空间中方位角度不同但拥有相同的坐标原点,即空间点p的位置并未发生改变但其坐标系发生了旋转,则可用旋转矩阵BpC表示坐标系的方位,即存在转换关系:

坐标系的变换往往不是单一平移与单一旋转那么简单,通常都是平移与旋转的复合变换,位置矢量ApB、旋转矩阵BpC分别表示坐标系{B}相对于坐标系{A}的平移变换关系和坐标系{C}相对于坐标系{B}的旋转变换关系,则空间点p在坐标系{A}下的位置矢量Ap有:

2 机器人运动学分析
在研究机器人运动学过程中并不考虑各种运动附加力对机器人的影响,只考虑机器人各连杆及关节的运动特性,机器人正运动学则可看成是已知机器人各个连杆的物理参数以及关节角度变量,求取末端执行器相对基坐标系的位姿关系[3]。
2.1 机器人结构模型描述
使用经典D-H参数法,需要确定机器人各相邻关节的坐标系间的转换关系,建立相邻坐标系间的转换矩阵。坐标系的创建如图2所示。
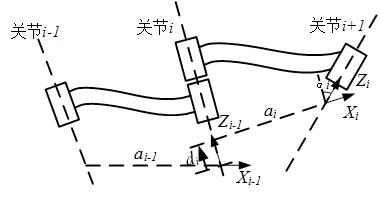
图2 D-H法各连杆关系示意图
坐标系的Z轴为各关节轴的中心轴线,坐标原点为各轴线公垂线的交点;X轴经过各轴的公垂线,方向为指向离开轴线的方向;而Y轴可用右手定则确定。并得出结构参数杆长di、扭转角αi、关节长度ai以及关节转角θi。
2.2 机器人正运动学
UR10是六自由度串联机器人,可实现高达10Kg的自动化作业,延伸半径范围1300mm,具备协作性与安全性[4]。根据其机械结构参数采用D-H进行连杆坐标系的建立,如图3所示。

图3 UR10机器人D-H坐标系
由于UR10机器人各关节均为转动关节,因此在机器人系统中只有关节角θ为变量,其余三个参数均为固定值,D-H模型参数如表1所示。

表1 UR10机器人D-H模型参数
依据机器人连杆坐标系以及D-H模型参数表,求解出连杆坐标系之间的齐次变换矩阵:

将表1中参数代入式(13),利用各连杆的转换矩阵进行相乘即可求解机器人的末端位姿:

其中nx,ny,nz,ox,oy,oz,ax,ay,az为机器人的末端姿态分量,px,py,pz为机器人的末端位置分量。
2.3 机器人逆运动学分析
在实际应用中往往指定机器人末端位姿,通过计算求得机器人到该位姿情况下的各关节转角变量,并驱动机器人移动到该位置下。这种求解各关节变量的过程即为机器人逆运动学分析[5]。
2.3.1 机器人逆运动学求解方法
一般情况下求取机器人逆解的方法主要有数值求解法与封闭法求解两种。通常六自由度的机器人主要采取数值求解法,但在某些特殊情况下求得的结果不是唯一解。而封闭法又分为几何求解法与代数求解法两种,相比于几何求解法,代数求解法计算更简单、通用性较强,成为求取机器人逆解的基本方法[6]。
2.3.2 机器人逆运动学分析
因UR10机器人的第二、三、四关节轴均为平行状态,满足逆解存在的条件,因此该机器人的逆解可通过数值求解法求得,求解结果如下:


上述求解机器人的相关逆解,但逆解的数量不是唯一的,可能会得到8组机器人的逆解,这就需要通过机器人的约束关系来选取逆解中最符合要求的一组作为机器人当前位姿的解。
3 UR10机器人运动学模型仿真
3.1 运动学模型建立
为了验证上述推导的数学关系是否正确,采用Robotics Toolbox工具箱对机器人进行运动学仿真,依据表1所提供的数据,对UR10型机器人进行仿真如图4所示,控制界面如图5所示。

图4 UR10机器人仿真

图5 滑块控制图
3.2 机器人正运动学验证
为了验证机器人正运动学方程和运动学模型的正确性,随机选取2组关节变量值,对图6中滑块控制器中各关节角度赋予变量值,读取控制器中机器人末端执行器的位姿;将随机选取的关节值同表1中UR10型机器人的D-H参数一同代入到机器人正运动学方程中,解出末端执行器的位姿;最终将滑块值与计算值对比。随机选取2组关节变量值,如下:q1=[0.2059 -1.2294 -2.6050-0.6161 2.4627 0.3317],q2=[1.8491 -1.3127 -1.4234-2.1205 1.1045 1.8834]。

表2 滑块值与MATLAB计算值比较
上述方法得到的结果在表2中列出,可以看出理论值和计算值的误差非常小,几乎可以忽略不计,证明了推导得出的机器人正运动学方程以及运动学模型是正确的。
根据2.3节机器人逆运动学求解方法,编写程序,定义机器人末端位姿W=[px,py,pz,ax,ay,az],将其代入程序即可求得机器人多组运动学逆解Qi=[θ1,θ2,θ3,θ4,θ5,θ6]。将两末端位姿W1=[-158.321,181.853,157.927,-0.318,0.729,-0.607]与W2=[-109.925,-295.804,835.089,0.397,0.247,-0.884]代入程序,再根据机械结构约束筛选出有效逆解,分别如表3,表4所示。
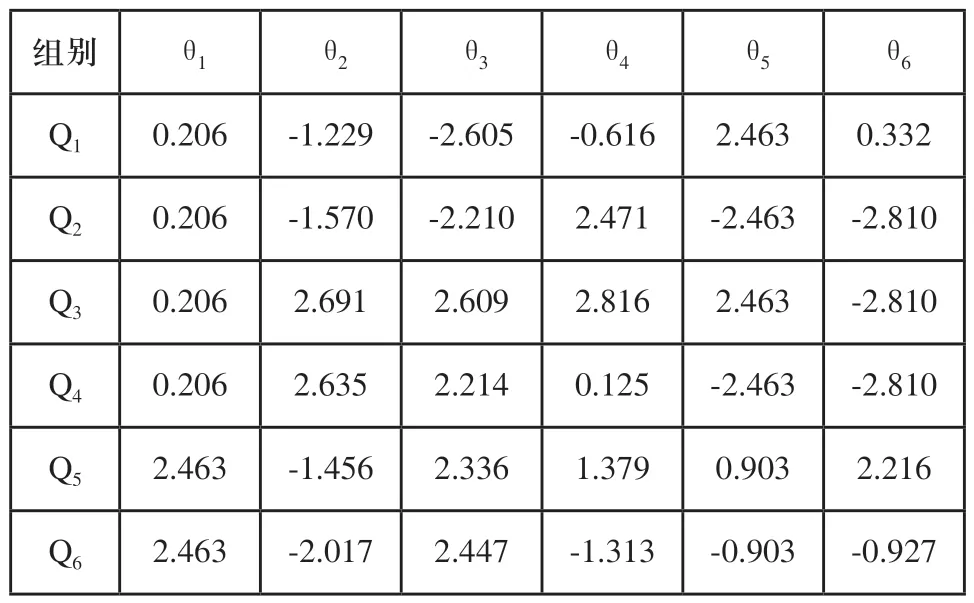
表3 位姿W1的运动学逆解

表3 (续)

表4 位姿W2的运动学逆解
每个位姿可以获取8组解,由于机器人机械结构约束与各杆件运动时不存在干涉,因此求得的8组解均为机器人的逆解。通过数据对比可知,表3中的Q1与上一节的q1相等,表4中的Q1与上一节的q2相等,验证了逆运动学的正确性。
4 结语
对UR10智能协作机器人进行相关结构建模,求解出机器人的D-H模型参数,并对机器人的正逆运动学进行分析,求解出正运动学中各连杆坐标系的转换关系以及逆运动学中各关节转角的求解方法。并用MATLAB进行了运动学的仿真与方程计算,通过数据对比分析验证了其运动学模型与运动学正逆运算的正确性。

