基于有限元的机械收获开心果的动力学分析
魏 娟,闫 豪,2,李 莹,郑 欣
WEI Juan1 , YAN Hao1,2 , LI Ying1, ZHENG Xin1
(1.西安科技大学 机械工程学院,西安 710054;2.上海汽车集团股份有限公司乘用车郑州分公司,郑州 450000)
0 引言
开心果外形尺寸较小,不易收获。目前主要依靠手工或简单的手持工具进行采摘,效率低且成本高,开展机械化采收作业具有重要意义。蔡菲等通过高速摄像对果实采收过程的研究发现,果实脱落的瞬间是速度差最大的时候,并且使果实脱落的力主要是由弯扭产生的[1]。彭俊等利用有限元方法对沙棘树进行动力学研究,通过分析关键点的应力值发现14Hz和180~280N的振动载荷可以确保大多数沙棘果实从树上分离[2]。吕梦璐等借助高速摄像仪,对杏果实在振动采收过程的运动规律、果实振动脱落时的速度变化规律进行了研究[3]。王冬等对3种典型整形果树进行模态分析和振动响应特性仿真分析,表明3种典型整形果树的低阶固有频率主要集中在7~11阶范围,分别在13.5、12.0和7.5Hz时振动响应最为剧烈,且一致性较好[4]。付威等建立红枣“枝—柄—果”的双摆振动模型,利用振动测试系统进行试验,表明在振幅为7mm、频率为17Hz时,红枣振动采收过程中,力的传递效果较好[5]。
综上所述,国内外对林果收获方面已有较多研究,针对开心果机械化振动采收的动力学研究还未见报道。本文采用农机与农艺相结合的方法,以整形开心果树为例,将果树关键点加速度作为落果条件,结合SolidWorks建模软件和ABAQUS分析软件,对开心果树的有限元模型进行振动采收仿真,分析各激振参数对关键点加速度的影响规律。
1 果树有限元建模
由于果树的生长特性多样性,在实际振动收获中激振功率受果树形态影响较大[6,7]。为提高采收效率,采用农机与农艺相结合的方式对果树进行削枝整形,将果树枝条和树冠整理成形态近似的结构和形状,使其适合于机械化采收作业,在此基础上进行收获机设计,能够保证设计的普遍应用性,对于采收效率的提高具有重要意义。
开心果树因其无中心主干具有矮干,属于自然开心形。整形后主干选留几个侧枝向外斜向上生长,每个侧枝分生2~3个侧枝。
1.1 果树的三维实体模型
开心果树通常树高3000~5000mm,树干直径240~310mm,树干高度550~1100mm,冠宽5000~6000mm。由于树体的形状不规则,所以将树干和分支定义为变量截面不规则旋转体。果实的收获经验表明:侧分支在振动收获过程中对主振枝影响很小[8],因此为提高计算效率将树体进行简化,通过实体测绘并利用三维建模软件SolidWorks中放样命令所建的开心果树三维模型如图1所示。

图1 开心果树及三维模型
1.2 果树的有限元模型
将树体的三维模型导入ABAQUS中,有限元单元采用C3D10,其由10个节点定义,每个节点有3个沿X、Y、Z方向平移自由度。由于果树根系与土壤之间作用力的复杂性,采用将根部和土壤固定的近似方式,约束根部X、Y、Z方向自由度。参考已有参考文献,表1列出树体材料参数,使用自由网格划分技术进行网格划分,得到树体有限元模型。
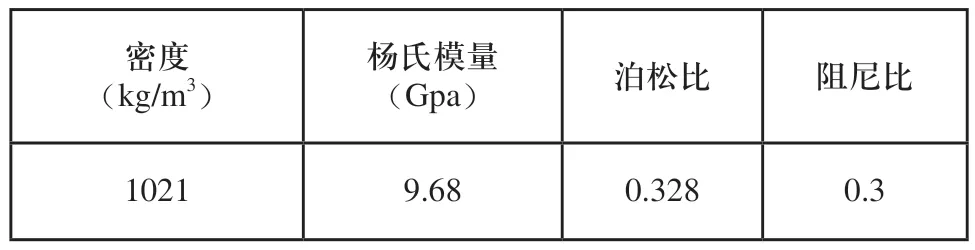
表1 开心果树的材料属性表
2 有限元模态分析
共振时的破坏作用可以带来较为理想的分离作用,使果实和果树分离。模态分析可以较为精确地识别果树结构共振时的固有频率和模态振型[9],为果树的振动特性分析提供参考。振动收获时需要的作业扭矩较大,驱动机构转速范围一般为0~2000r/min,工作频率为0~33.3Hz,因此模态分析主要考虑前15阶模态,频率范围0~58.6Hz。模态分析采用Lanczos法求解,各阶模态频率如表2所示,选取典型阶次模态云图如图2所示。
从表中看出低阶模态频率成对出现,大小接近且振型相似,分析原因是分别对应x向、y向自由度,在之后分析中将其视为一组分析。由模态云图可以看出在第1阶、第4阶、第5阶模态,各次级分枝末端有显著响应,树干和侧枝下端响应很小,符合振动收获时理想的响应特性要求。

表2 主要模态频率表
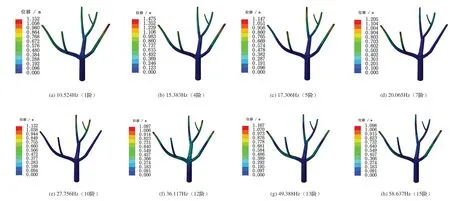
图2 典型阶次的模态云图
3 果树振动响应特性分析
将树体等效为悬臂梁结构,分析其弯曲振动特性。
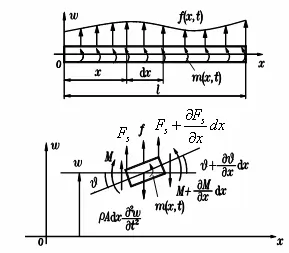
图3 悬臂梁及其微段受力
由图3可得其弯曲振动微分方程为:
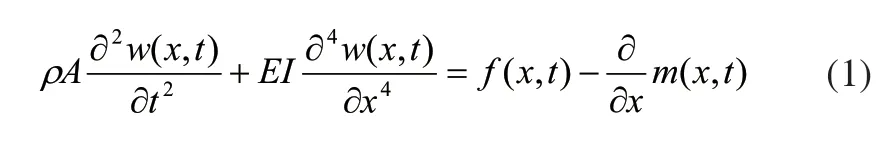
由于树体为无限自由度系统,且为变截面不规则非线性系统,式中各特性参数实际中很难得到准确值,因此难以通过定量计算得到其稳态响应W(x,t)。谐响应分析作为一种有限元分析技术,可以预测结构受到简谐载荷时的连续动力特性[10]。果树振动收获时所施加的载荷通常是周期性的简谐力,本文通过对果树进行谐响应分析,模拟振动收获试验,分析果树在特定频率范围内的位移和加速度响应。
3.1 3种加载方式响应分析
常见振动收获机多采用惯性激振器,通过偏心块高速旋转产生激振力。偏心块布置形式不同可以产生不同形式的激振力,图4所示为3种收获机结构原理图。
为便于对比分析,三种加载方式合力均取500N。图5所示为果树模型在双体平衡、双体多向型、单体回旋型激励方式下关键节点的振动响应特性。
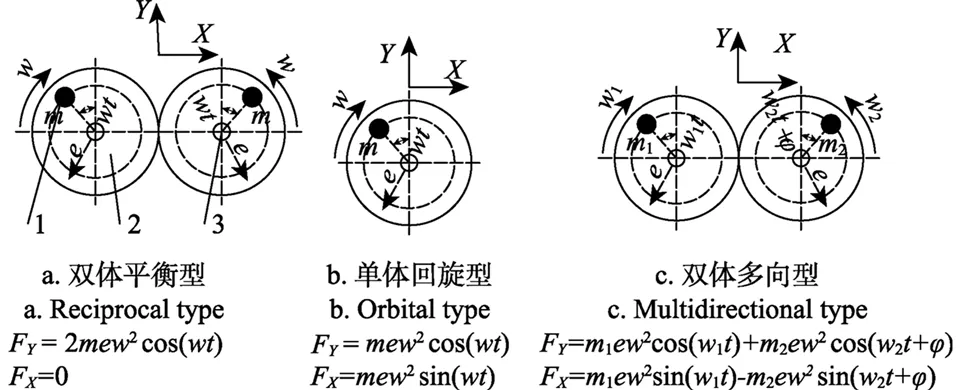
图4 常见惯性激振装置结构示意图
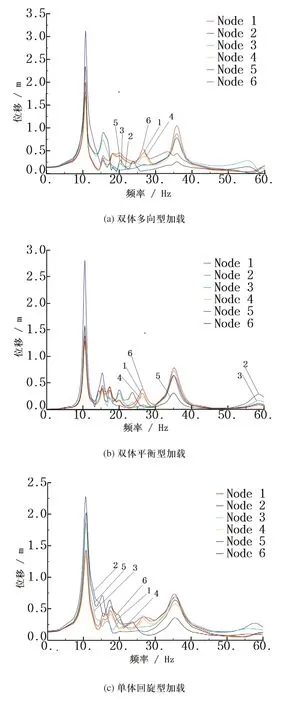
图5 3种加载方式下的振动响应特性曲线
3种激励方式均可得到较为理想的振动响应,双体多向型激励产生的振动位移响应较其他两种激振方式更为剧烈。在10Hz、14~18Hz和35Hz时位移幅值更大,分别对应模态的第1~6阶和11阶模态频率。由于35Hz超过常用驱动机构转速范围不予考虑,仅对10~18Hz频率范围进行定频分析。
3.2 定频振动分析
振动收获时果实在激励力的作用下按一定方式摆动,当振动产生的惯性力大于果实与果柄的分离力时,果实脱落完成收获。惯性力源于加速度,因此加速度响应是果树动力学中重要特性之一[11]。由实验结果得出在开心果的成熟阶段,脱落时加速度变化规律如图6所示[12],随着成熟时间线性下降,取12000mm/s2作为此次分析的果实脱落条件。
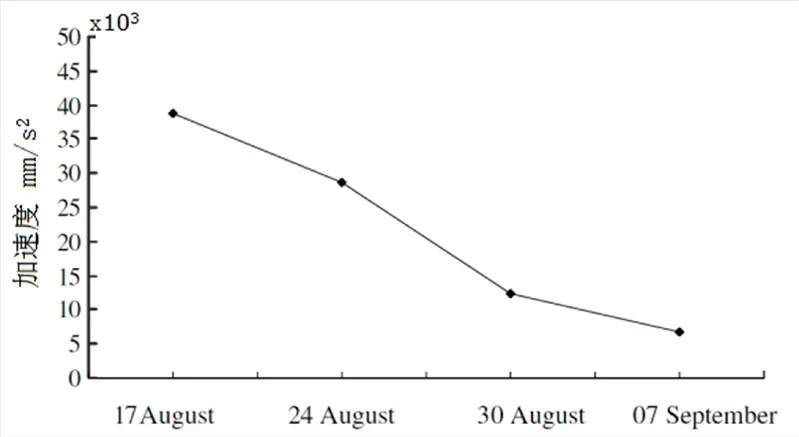
图6 开心果脱落时加速度随成熟度变化曲线
由于振动机构的激振频率很难精确固定在某一频率点,且仿真得到的固有频率存在误差,所以应更关注共振频率两侧一定范围内频率段。根据模态分析和谐响应分析结果,将10~18Hz频率段分为10~12Hz、13~15Hz、16~18Hz三段,定频分析果树加速度响应。
3.2.1 力作用点高度分析
作用点位置过低会导致果树根部振幅过大造成损伤,位置过高影响收获时安全性。分别选取700mm、900mm、1100mm进行分析得到关键点加速度响应如图7所示。通过统计分析,找出每个频率段各节点加速度最大值、最小值,并计算6个节点加速度的平均值和变异系数,如表3所示。
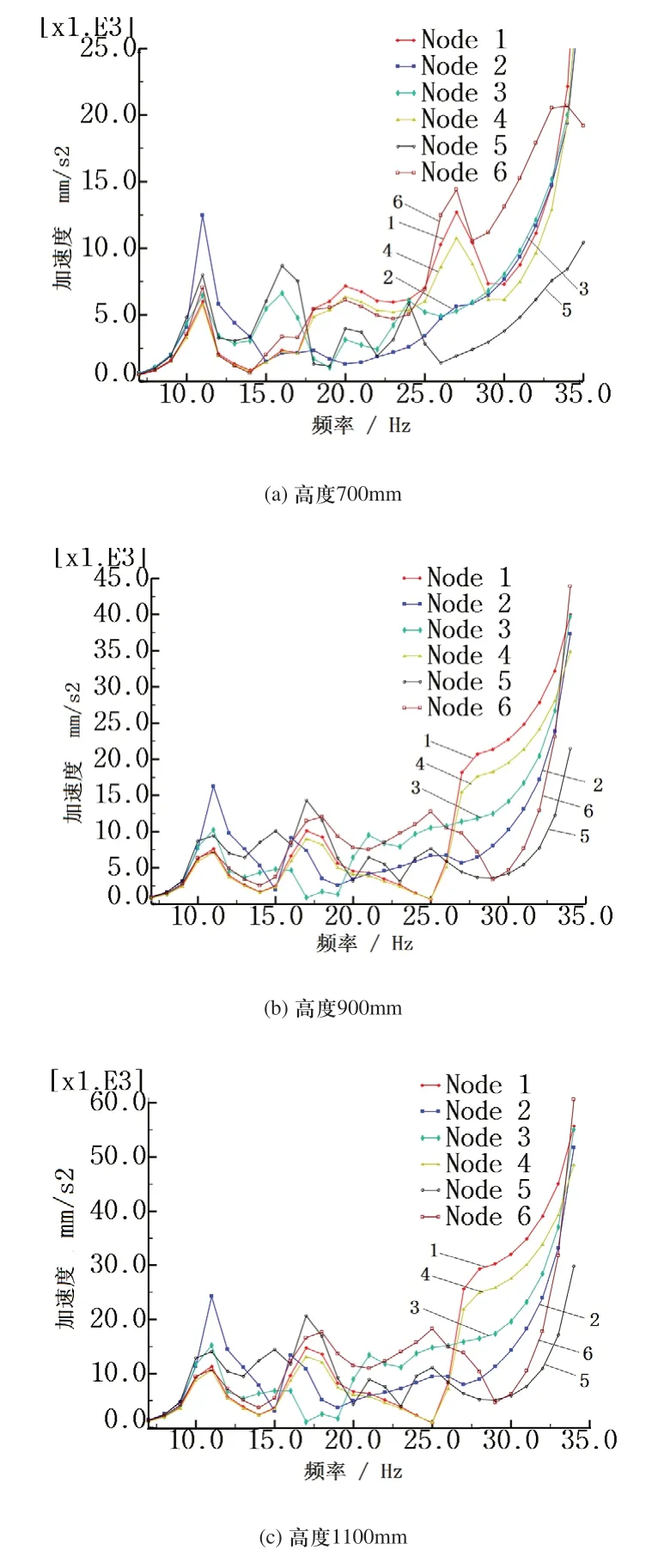
图7 3个力作用点高度下加速度响应曲线
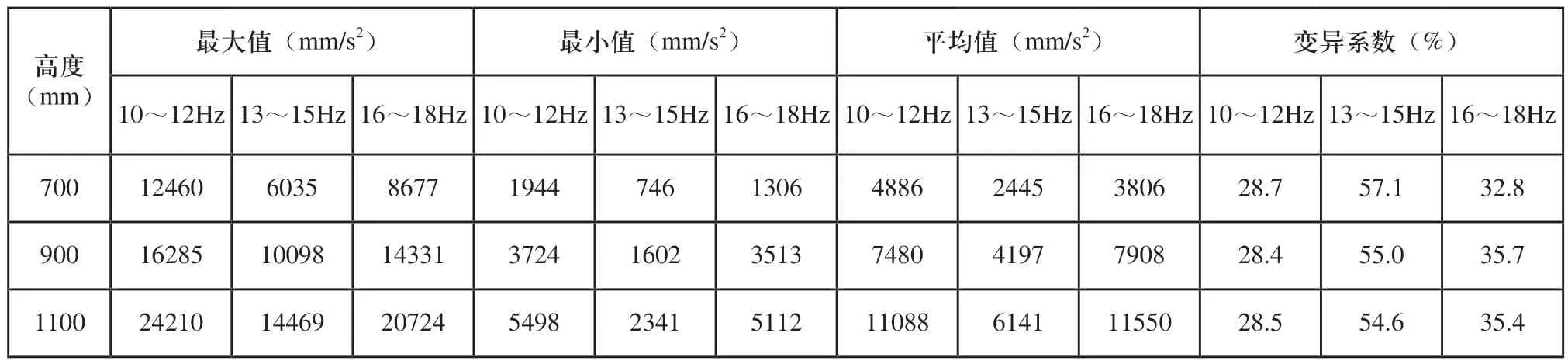
表3 3个频率段节点加速度
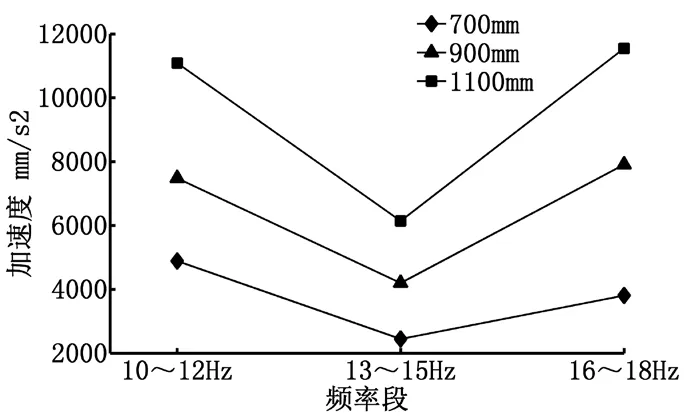
图8 3个力作用点高度下各节点加速度响应平均值
分析表3和图8,10~12Hz和16~18Hz频率段加速度响应较13~15Hz频率段更加剧烈,且13~15Hz频率段变异系数较大,故13~15Hz不适用于振动收获。随着力作用点高度增加,各频率段节点加速度响应逐渐增大,变异系数变化不大。瞬时加速度值随力作用点高度增加变化不明显,节点的加速度值大部分都小于12000mm/s2,因此通过提高作用点高度使果实达到脱落条件是低效率的。
3.2.2 激振力幅值分析
谐响应分析是对结构的稳态响应进行的线性分析,因此可以通过如下线性方程求得合适的激振力:

式中:F1、F2为激振力;
a1、a2为加速度。
对10~12Hz和16~18Hz频率段进行分析,取激振力500N时,16~18Hz各节点加速度平均值3806mm/s2计算得出需施加激振力,大小取为1600N,仿真结果得到各节点加速度响应如图9所示。通过统计分析,计算各频率段6个节点加速度的平均值,如表4所示。
由图10可知10~12Hz和16~18Hz频率段各节点加速度平均值均超过12000mm/s2,小频率可以节约能源,故10~12Hz频率段是最佳激振频率。振动载荷为1600N时可以使大部分果实从树体脱落完成收获。
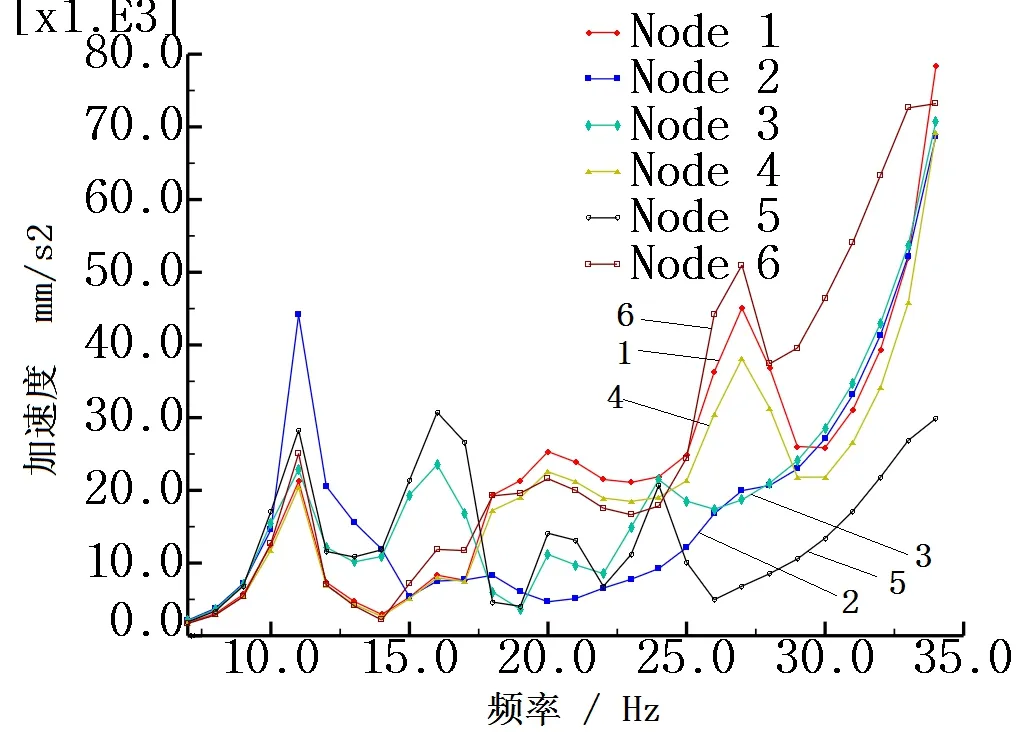
图9 振动载荷为1600N时各节点加速度响应
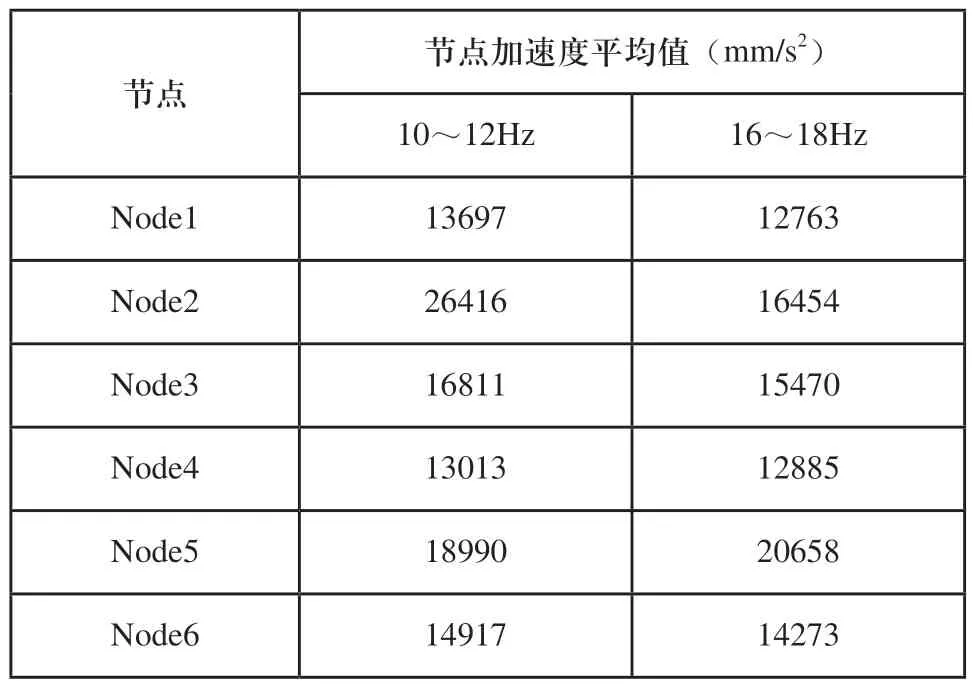
表4 各节点加速度平均值
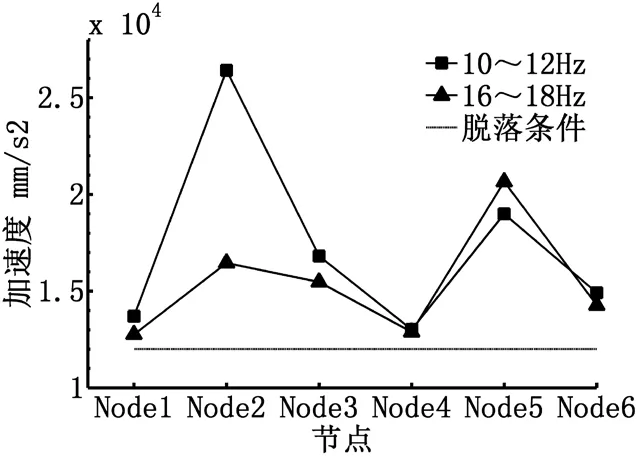
图10 各节点加速度平均值
4 结论
本文通过有限元建模,进行动力学仿真实验,对开心果树的振动采收中果树动态响应进行了研究,试验结果表明:
1)开心果树的前15阶固有频率范围为10.5~58.6Hz,在10.5Hz(1阶)、15.3Hz(4阶)、17.3Hz(5阶)时振型响应一致性较好。
2)激振力的3种加载方式中,双体多向型更适合于开心果采收,各分枝末端位移响应幅值更大。
3)通过线性分析得出最佳激振力以达到果实脱落条件,比不断提高力作用点高度更为高效。
4)10~12Hz频率段是最佳激振频率,各节点加速度响应最为剧烈。振动载荷为1600N时,各节点加速度平均值均能达到果实脱落条件,确保果实脱落。

