优化数学活动的前提
王丽琼
数学活动是指“通过观察、实验、猜测、验证、推理与交流、反思、问题解决等方式,让学生从已有的生活经验和现实背景中获取数学事实,形成数学化,旨在使学生真正理解和掌握基本的数学知识和技能、数学思想和方法,获得广泛的数学活动经验,培养实践能力和数学素养的思维、实践活动”。数学活动必须有明确的数学内涵和数学目的,体现数学本质。教学中,必须设计符合内容特征的数学活动,才能更好的发挥数学活动的作用,达成教学目标。下面以《比大小》为例谈谈具体的做法:
㈠、数学活动的设计——依纲据本,遵循认知,把握教学内容
《比大小》是北师大版三年级下册第五单元《认识分数》中的一部分。分数大小比较的学习分为两个阶段,三年级要学习的《比大小》主要是同分母分数大小的比较和同分子分数(分子是1)大小之间的比较。本节课教材分三步进行教学:第一步借用直观面积模型比较同分母分数大小;第二步借助一组同分母分数,进一步体会分数大小的比较;第三步结合画图的方式,巩固同分母分数的比较,学习分子是1的异分母分数的大小比较;且小学三年级学生的思维认知正处于形象思维到抽象思维的过渡阶段。由此,我们从教材实际出发,以学生的认知规律特点为指导,设计了三个的数学活动:活动一,分实物,初步感知同分母分数大小的比较方法。从学生喜欢又熟悉的悟空、八戒分西瓜入手,利用学生已有的生活经验和认知经验,直观地感知同分母分数大小的比较方法;活动二,涂图形,进一步体会同分母分数大小的比较方法。借助直观面积模型,帮助学生比较分数的大小,学生在涂一涂、比一比的活动中,进一步体会到当平均分的份数相同时,取的份数越多即含有的分数单位越多,分数越大;从而脱离直观,抽象出利用分数的意义,直接比较的本质的方法;活动三,借图形,自主探究分子1的异分母分数大小的比较方法。这一环节,放开时空,让学生借助前面的经验自主探究,培养学生的探究意识和能力,引入分数墙,帮助学生理解单位“1”相等时,平均分的份数越多,每一份越小的难点。这样的设计数形结合,遵循学生认知特点,实物比较——图形比较——抽象比较,帮助学生理解分数大小的关系,建构分数大小比较的本质的方法。
㈡、数学活动的设计——活用教材,大胆创新,拓展教学内容
研读教材时,我们認为教材问题串的问题一、二、三均是让学生在图形上涂出分数,再比较大小,形式单一,而且费时间(学生涂得慢)。因此,我们把问题一改为学生喜欢又熟悉的悟空、八戒分西瓜的情景,学生口答(节省时间),让学生在直观的分实物中初步感知同分母分数大小的比较方法,从而引出3/4﹥2/4﹥1/4的事实。问题二,改为每人涂一个,节省时间的同时,逼迫学生思考,引出6/6﹥5/6﹥4/6﹥3/6﹥2/6﹥1/6的分数串,分数串更凸显同分母分数大小的特征,为归纳概括同分母分数大小的比较方法提供充分的感性材料。问题三,变为自主探究,利用不同的图形表征,让学生感受分子1的异分母分数大小的比较方法,再引入分数墙,帮助学生理解单位“1”相等时,平均分的份数越多,每一份越小的难点,得出分数串1/2﹥1/3﹥1/4﹥1/5﹥1/6﹥1/7﹥1/8﹥1/9﹥1/10,在此基础上归纳概括出比较方法。教材中均是两个分数的大小比较,我们大胆创新,引入分数串,拓展了教学的内容,促进学生的思维广度和深度的发展,培养了学生自主探究问题,大胆想象的能力。
㈢、数学活动的设计——斟酌环节,承前启后,服务教学内容
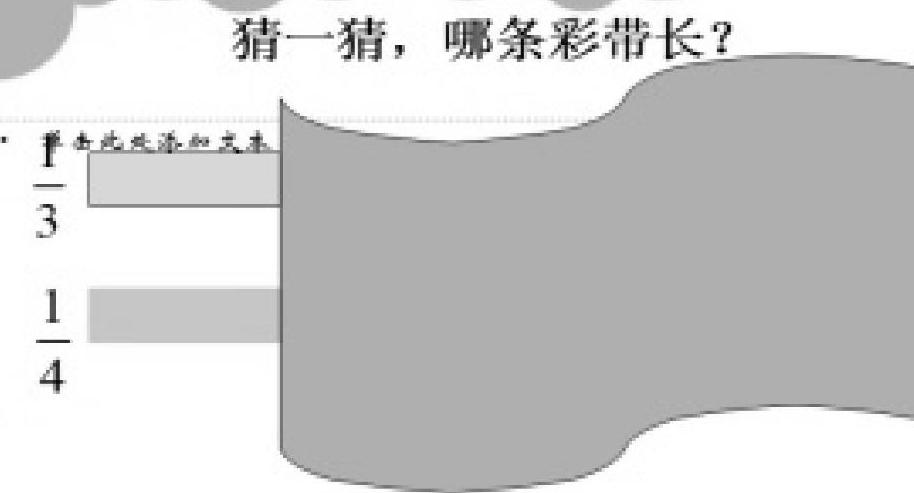
教学核心问题是教学目标落实到教师课堂教学行为和学生学习活动之上的具体化,即教学活动的可操作化。因此,在设置具体的教学环节时,应以教学目标为方向,以更好服务教学核心问题为主导,承前启后。如:活动一,分西瓜环节的设置:承前是让学生借助熟悉的生活背景,复习分数的意义;启后是沟通分母相同的分数大小与分数的意义之间的联系,从而引入活动二的探究环节。活动二,涂图形环节的设置:承前是利用图形这个载体,探究分母相同的分数大小的比较方法,在即时练习中设置引发认知冲突的题目1/2○1/4,就为启后下一环节。活动三,生自主探究1/2○1/4,承前是让学生用已有的利用图形探究的经验来学习,分数墙的引入既突破难点,又为启后的继续学习打下基础。练习题的设置,既是巩固所学知识内容(承前),又要考虑启后的作用,给学生一个发展性的学习观念。如:哪条彩带更长呢?
这一问题的设置,引发学生认知冲突,激发学生进一步探究的欲望,为以后的进一步学习伏笔,后面较难分数应用题与此题异曲同工:学校图书馆有科技书和故事书共630本,科技书的1/3与故事书的1/4相等,学校科技书、故事书各有多少本?
可见,设计教学活动前,研读教材是必要的也是必须的。读懂教材的呈现内容,读懂教材的编排意图,读懂知识的前缘后生,读懂学习教材的学生…深读教材,读透教材的广度和深度,做足准备后设计的课才能有的放矢,才能达到事半功倍的教学效果。
(作者单位:福建省泉州市永春县桃城镇中心小学)

