我对《三角形面积》教学的再思考
张瑜


《三角形面积》是在学生学习了平行四边形面积计算,初步感受了转化思想的基础上进行的,它是平行四边形面积计算的延伸,又是后面梯形面积计算的铺垫,是具有承前启后的作用。让学生明白三角形面积计算公式不是最终目的,更为重要的是知道公式是怎么来的。所以本节课的价值定位不是“公式应用”,而是三角形面积的“公式推导”,重点是让学生经历一系列的数学活动,探索并理解三角形的面积计算公式,体会转化方法的价值,培养学生应用已有知识解决新问题的能力,发展学生的空间观念和初步的推理能力。
在教学平行四边形面积公式推导的时候,只需要将平行四边形沿高线剪下一部分,通过平移转化成长方形,即可推导出平行四边形的面积计算公式。这一层次的活动只是把图形进行简单的分割和组合,而不是有预见地去构造新的几何图形,大部分学生能主动完成这样的建构活动。
在教学三角形面积计算公式的时候,教材是这样的呈现:例4:利用方格图素材,学生通过观察对比,思考分析出三角形面积的求法,涂色的三角形面积就是它所在的平行四边形面积的一半。进而得出这样的结论:一个平行四边形可以分成两个完全一样的三角形,其中一个三角形的面积是所在平行四边形面积的一半。初步感知三角形面积与平行四边形面积之间的关系。为后面用两个完全一样的三角形拼成一个平行四边形作了很好的铺垫。例5:通过前面的学习学生积累到“转化”经验,初步认识平行四边形能分成两个完全一样的三角形,那么两个完全一样的三角形也能拼成一个平行四边形。通过操作——计算——观察——归纳的过程,进一步明确三角形与其拼成的平行四边形的关系,从而推导出三角形面积公式。在教材的最后,“你知道吗?”环节中,介绍了中国古代《九章算术》的三角形面积解法,帮助学生理解另一种转化求面积的方法——中位线分割法,进一步拓展学生的思路。
照这个思路上课的话,我们会感觉很“顺”,但是在顺的背后是老师设计的一个个铺垫让学生失去了主动探究的机会,如果没有例4的铺垫当学生面对一个独立的三角形时,能想到再去构造一个完全一样的三角形拼成一个平行四边形吗?显然学生的这个思维活动是被动的,受牵引的。用两个完全一样的三角形拼成一个平行四边形,进而利用平行四边形面积推导出三角形面积。在这里我们把它简称为“倍拼”思路,“倍拼”思路其实是一种图形构造能力,它不是一蹴而就的,也不会单纯随年龄增长而进步的,这与学生的活动经验是分不开的。当学生面对一个三角形时,并不能主动想到要构造两个完全一样的三角形来拼成平行四邊形。这里学生的“倍拼”思路是在老师的授意下、教具学具的暗示下被动形成的。那么怎样才能让学生主动完成这样的“倍拼”呢?我进行了以下的尝试:
没有任何铺垫,直接利用方格纸素材,给学生呈现3个独立的三角形,分别是锐角三角形、直角三角形和钝角三角形。
师:这里的方格纸上有3个三角形,你会求哪个三角形的面积?
(大部分学生在尝试的基础上选择求2号三角形也就是直角三角形的面积)
师:那我们就先来研究2号三角形的面积是如何计算的?
(受前一节课平行四边形面积推导过程的影响,学生容易想到把直角三角形进行分割组合成一个新的长方形。)
师追问:怎样分割才能拼成长方形?拼成的长方形和原来三角形之间有什么联系?
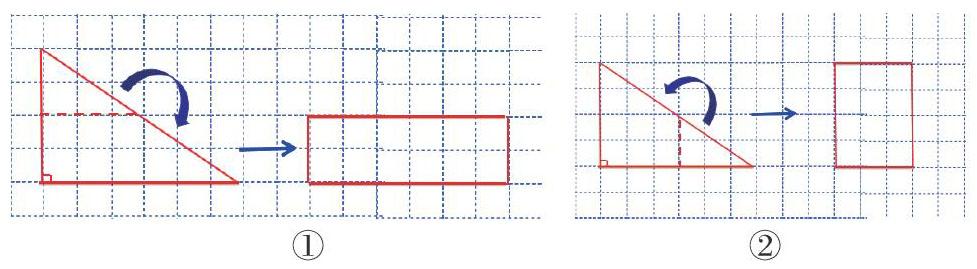
强调必须要沿着三角形的中位线分割才能拼成长方形。拼成的长方形的面积就是三角形的面积,拼成的长方形的长是三角形的底,长方形的宽是三角形高的一半(如图1),拼成的长方形的长是三角形的高,长方形的宽是三角形底的一半(如图2)。
也有学生在这个直角三角形的“对面”画一个和它一样的三角形(如图3),把它补成一个长方形,从而得出三角形的面积是长方形面积的一半。
最后总结出:直角三角形的面积=底×高÷2
师:那么1号和3号三角形的面积是否也可以用底×高÷2来计算呢?你们有办法算出它们的面积吗?请小组商量,合作完成。
(提供给学生学具袋,里面有完全相等的锐角三角形两个,完全相等的钝角三角形两个,等底等高的三角形两个,方格纸上呈现单独的锐角三角形和钝角三角形各一个。)
有了直角三角形这个特殊三角形为中介,学生能主动完成“倍拼”的构想,同时中位线割补法也可以被借鉴到锐角三角形和钝角三角形中。
以上的教学过程把三角形面积的探索过程还给了学生,符合数学发现的历史事实,其高明之处就是在于没有限定学生的思维,没有了条条框框,把“推导”这个包袱完全抛给了学生,这样更能体现探究学习的真义。

