推挽式变换器的电磁设计与计算

一、研究背景

开关电源技术作为当下社会一种最近兴起的技术，因其所占空间小、质量轻、转换成果高，在当代世界的各个领域的电子产品中有着至关重要的位子。开关电源分为交流变直流、直流变交流、直流变直流；即(AC/DC)、(DC/AC)、(DC/DC)三种功率变换，它们基本都是由DC/DC变换器主回路和电源集成控制芯片构成，而其主要部分是DC/DC变换器，而其中常见的就有推挽式变换器。[1]

二、推挽式变换器的电磁设计

(一)工作原理

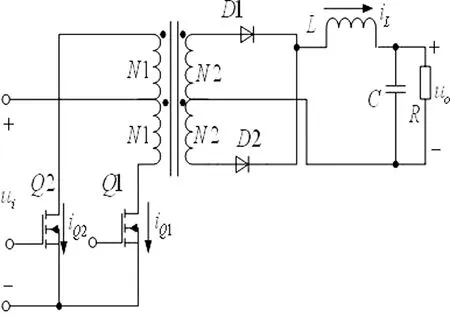
图1 推挽式变换器

图1所示为推挽式变换器的工作电路图。

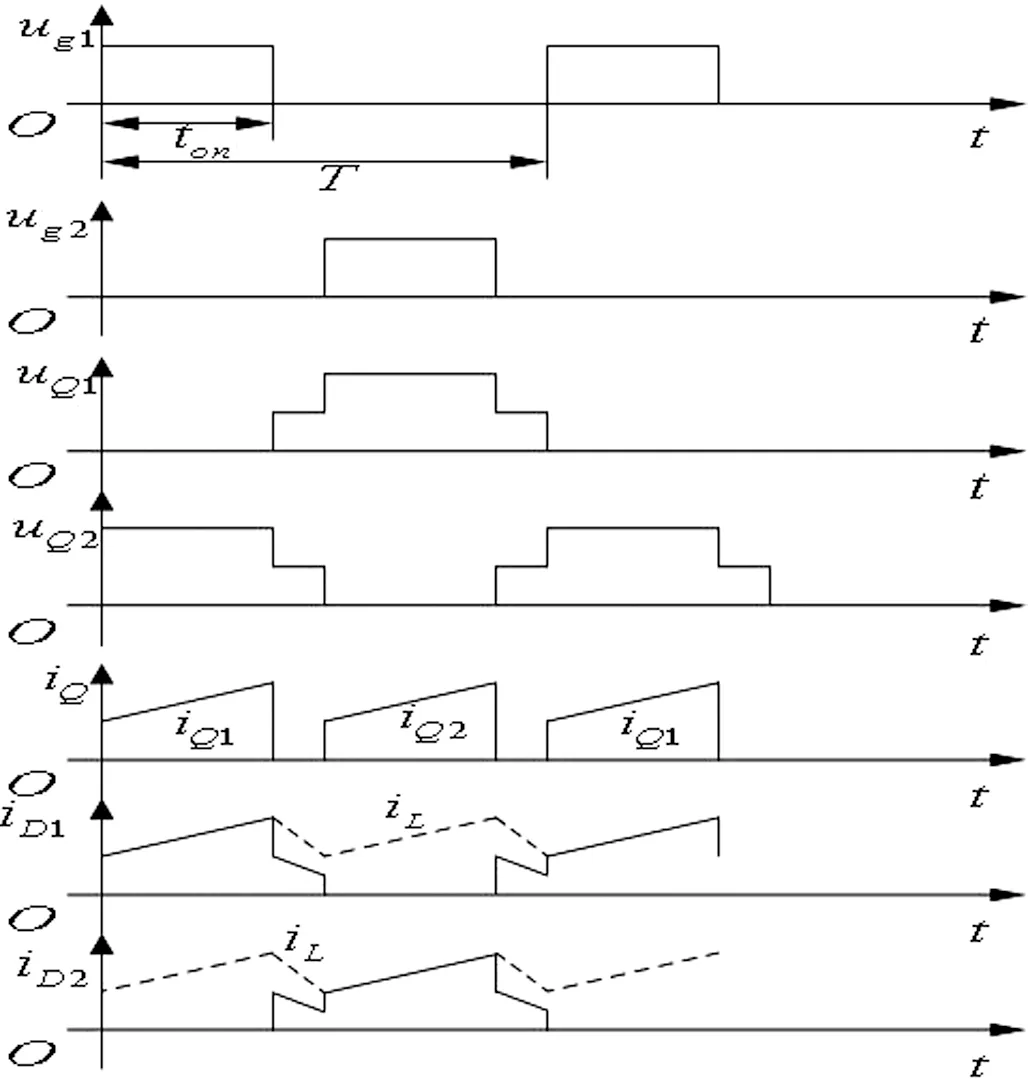
图2 推挽式变换器工作波形

图2所示波形推挽变换器的工作波形。

推挽电路中两个开关Q1和Q2交替导通，在绕组N1和N1’两端分别形成相位相反的交流电压。Q1导通时，二极管D2处于通态，Q2导通时，二极管D1处于通态，当两个开关都关断时，D1和D2都处于通态，各分担一半的电流。Q1或Q2导通时电感L的电流逐渐上升，两个开关都关断时，电感L的电流逐渐下降。Q1和Q2断态时承受的峰值电压均为两倍的输入电压。[2]

如果Q1和Q2同时导通，就相当于变压器一次绕组短路，因此需避免两个开关同时导通，每个开关各自的占空比不能超过50%，还要留有死区。[2]

(二)技术参数

推挽式变换器的技术参数设定为输入电压36～72V，输出电压24V，输出电流12.5A，频率50KHZ，理论温升35°，本文以此指标为例进行设计计算。

图1所表明为推挽式变换器的电路图，图2所表明的为该变换器的电压和电流波形图。在计算过程中，我们将原副边绕组设为相等，主要是简化计算过程。

由图2可以看出，占空比的定义为：t=0时，开关1导通；而在t=DT′时，开关1关断。由此可知，开关1和开关2一起工作的时间为DT，则输出电压就可以表示为Vo=DVs。电压波形被开关1和开关2在T′=T/2时所控制，即开关周期为T。

磁感应强度从零上升至最大值所需要的时间为=DT’/2=DT/4内。

根据输入电流与绕组电流有效值的关系，可以得到副边绕组电流的表达式为：

(2.1)

则二次绕组电压有效值的表达式可以写成：

(2.2)

就功率因数的概念而言，每个绕组的平均功率为

=Po/2，其中Po为总输出功率，从而可知每个二次绕组的功率因数可以用下式表示：

(2.3)

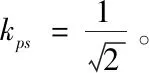
由于占空比的存在，输入电压以及输入电流应取有效值。传输的平均功率在每个一次绕组上的大小为：

(2.4)

每个原边绕组的功率因数在输入电流等于输出电流且原边绕组匝数等于副边绕组匝数时，可以由下式得到其功率因数：

(2.5)

然后，将一对一次绕组和一对一次绕组的功率等级相加。则可以得到每个二次绕组的平均功率为Po/2,并且每个原边绕组上的平均功率也为Po/2.那么，得到

(2.6)

根据以上公式计算发现不同的输入电压会有不同的占空比，即输入直流电压为36-72V时，占空比为0.33-0.67。因此我们设输入电压为最小值，即36V时，得到的占空比为0.67。

(三)磁心选择

在频率一定的情况下，只有Mn-Zn铁氧体符合上述推挽式变换器对磁心材料的要求，且其型号为EPCOS N87。

在这里将二极管的正向压降设为为1V，这样就可以得到其输出功率：

Po=(24+1.0)12.5=312.5W

对于上述所选择的磁心来说，最大占空比时必定发生最大损耗，即将最大占空比D=0.67代入式(2.6)中可得VA=935V。

依据最佳磁感应强度求值公式：

我们可以得到最佳磁感应强度值为：0.126T

其中：典型值ka=40，kc=5.6，kw=10，ρw=1.72×10-8Ω·m，hc=10W/(m2·°C)，

最佳磁感应强度只有在小于饱和磁感应强度时才不会受限制，因此由公式计算磁芯面积乘积Ap：

得到：Ap=4.81cm4

(四)绕组匝数及铜损的计算

(1)原边绕组匝数

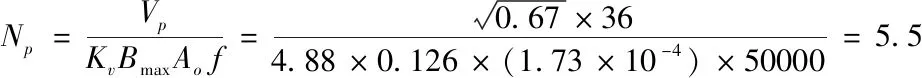
根据计算结果知原边绕组匝数为5.5匝，为了取整，故取为6匝。

(2)副边绕组匝数

为了计算简单，将原副边绕组匝数比设为相等。

(3)原边绕组铜损

根据公式计算得到原边绕组铜损为：

(4)副边绕组铜损

每个副边绕组铜损为：

(5)铜损

选择的磁心的磁感应强度最大值为

总损耗：

原边绕组铜损 0.185W

副边绕组铜损 0.215W

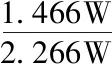
效率：

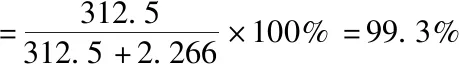
(8)温升的计算：

根据公式

即温升21.4℃。