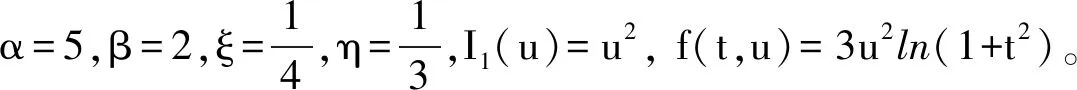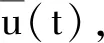非线性二阶脉冲微分方程解的正性的缺失
汪婷婷, 范虹霞
(兰州交通大学 数理学院, 甘肃 兰州 730070)
脉冲微分方程描述的是系统状态在某一时刻突发改变的过程,对其基础理论进行研究的文章已有很多,期间脉冲微分方程边值问题的研究也受到越来越多的关注[1-6]。在现有文献中,大多数学者致力于讨论脉冲微分方程正解的存在性,如文献[1]中,Feng和Xie利用锥压缩与锥拉伸不动点定理讨论了二阶脉冲微分方程m点边值问题的多个正解的存在性。而对脉冲微分方程边值问题非零解存在性的研究,却很少有学者关注。
2009年,文献[7]研究了二阶常微分方程边值问题
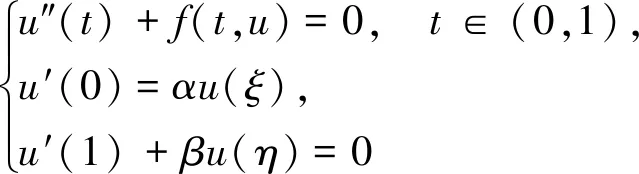
非零解的存在性,其中α和β是正参数。
受文献[7]的启发,本文主要研究下列二阶脉冲微分方程边值问题
(1)
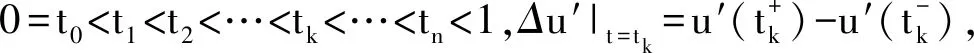
本文的主要工作是讨论当参数α或β增大时,相应积分方程的核函数的符号改变情况,并结合不动点定理给出问题(1)非零解的存在性,推广了文献[7]的结果。其他有关脉冲微分方程解的研究可参见文献[8-14]。
以下列出本文要用到的假设条件:
(H1) 1+βη>β;
(H2) 1-αξ>0;
(H3) 1+βη<β;
(H4) 1-αξ<0;
(A1) 1+βη≥β;
(A2) 1-αξ≥0。
1 预备知识
设J′=J{t1,t2,…,tn}。定义空间

本文主要结果的证明要用到以下的定理和相关引理。
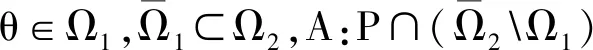
(ⅰ) ‖Au‖≤‖u‖,∀u∈P∩∂Ω1,‖Au‖≥‖u‖,∀u∈P∩∂Ω2;
(ⅱ) ‖Au‖≤‖u‖,∀u∈P∩∂Ω2,‖Au‖≥‖u‖,∀u∈P∩∂Ω1;
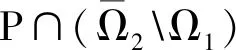
引理1 设Δ=α(1+βη)+β(1-αξ),f∈C([0,1]×(-∞,+∞),[0,+∞)),Ik∈C((-∞,+∞),[0,+∞)),则u∈PC1[0,1]∩C2(J′)是问题(1)的解当且仅当u是下列脉冲积分方程
(2)
的一个解,其中

(3)
证明必要性。
设u∈PC1[0,1]∩C2(J′)是问题(1)的解,对问题(1)中的方程两端积分可得:
(4)
对上式再次积分,可以得到:
(5)
在(4)式中,令t=1,并结合边值条件易得:
(6)
在(5)式中,分别令t=ξ,t=η,并结合(6)式有:
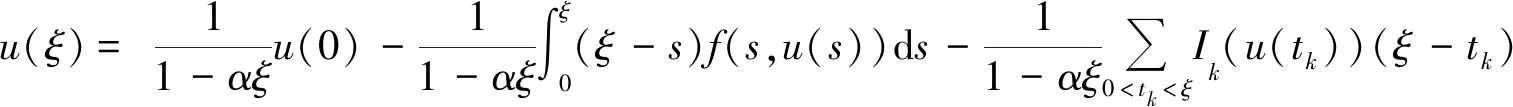
(7)
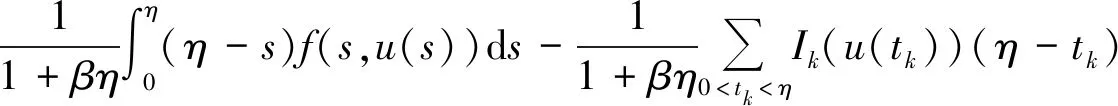
(8)
将(7)式和(8)式代入(6)式中化简可以得到:
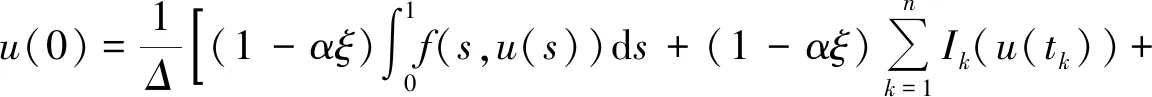
(9)
从而

(10)
结合(5)、(9)和(10)式化简易得:
其中
充分性。
设u(t)是脉冲积分方程(2)的解,则当t≠tk时,直接对(2)式求导得
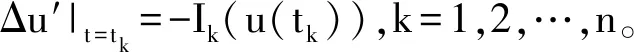
引理2[7]设条件(H1)和(H2)成立,则k(t,s)在[0,1]×[0,1]上为正,并且满足下列性质(P):存在一个可测函数φ:[0,1]→[0,+∞),子区间[a,b]⊂[0,1]和常数c,使得|k(t,s)|≤φ(s),t、s∈[0,1],并且
|k(t,s)|≥cφ(s),t∈[a,b],s∈[0,1]。
注1 由文献[7]引理2.2的证明知,这里
引理3[7]设条件(H3)和(H4)成立,则k(t,s)在[0,1]×[0,1]上改变符号,并且满足性质(P)。
注2 由文献[7]引理2.3的证明知,这里
引理4[7]如果条件(A1)和(A2)成立,那么k(t,s)在[0,1]×[0,1]上是非负的,并且满足性质(P);如果条件(A1)或(A2)之一不成立,那么k(t,s)在[0,1]×[0,1]上改变符号,并且满足性质(P)。
引理5 设条件(H3)和(H4)成立,则存在可测函数Ψ(s):[0,1]→[0,+∞),使得

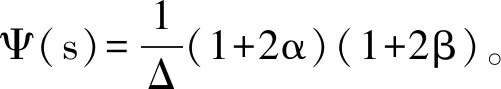
证明由(3)式,有
其中
情形1s≤η。若s≤ξ,s≤t,则
若s≤ξ,s>t,则
若s>ξ,s≤t,则
若s>ξ,s>t,则
情形2s>η。若s>ξ,s≤t,则
若s>ξ,s>t,则
2 主要结果及证明
定理1 设(H3)和(H4)成立,f∈C([0,1]×(-∞,+∞),[0,+∞)),Ik∈C((-∞,+∞),[0,+∞)),且在[0,1]的任意子区间上f(t,u)≢0。此外,设f和Ik满足下列条件:
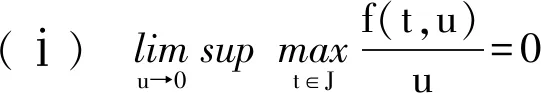
则边值问题(1)至少存在一个解u(t),满足u(t)>0,t∈[a,b]。
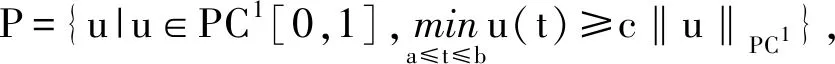
定义算子A:P→P
(11)
显然,问题(1)的解u(t)是算子A的不动点,可以验证A:P→P是全连续算子。
事实上,∀u∈PC1[0,1],有Au∈PC1[0,1]。由引理3和(11)式容易得到
且
由引理3、引理5和(11)式可求得
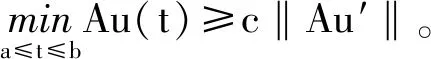
因此,∀u∈P,Au∈P,A是P→P的保锥算子。下面说明A是全连续算子。
显然算子A连续,容易验证算子A映射P中的有界集为有界集且A在每个区间(tk,tk+1)(k=0,1,2,…,n)上等度连续,由广义的Arzela-Ascoli定理可知A是全连续算子。


令Ω1={u∈PC1[0,1]:‖u‖PC1 从而‖Au‖≤‖u‖PC1。 又 则有‖Au′‖≤‖u‖PC1。所以 ‖Au‖PC1≤‖u‖PC1,u∈P∩∂Ω1。 (12) 因此‖Au‖≥‖u‖PC1。于是, ‖Au‖PC1≥‖u‖PC1,u∈P∩∂Ω2。 (13) 所以‖Au‖≥‖u‖PC1,从而‖Au‖PC1≥‖u‖PC1,u∈P∩∂Ω2。 定理2 设(H3)和(H4)成立,f∈C([0,1]×(-∞,+∞),[0,+∞)),Ik∈C((-∞,+∞),[0,+∞)),且在[0,1]的任意子区间上f(t,u)≢0。此外,设f和Ik满足下列条件: 则边值问题(1)至少存在一个解u(t),满足u(t)>0,t∈[a,b]。 类似定理1和定理2的讨论,由引理2可知,问题(1)至少存在一个解u(t),且满足u(t)>0,t∈[a,b]。同理,由引理4可以分别得到两个解的存在性定理,此处不再赘述。 例考察下列二阶脉冲微分方程边值问题 (14)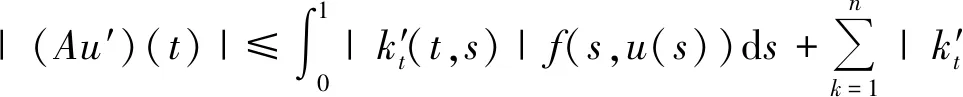
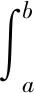
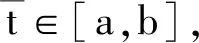
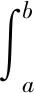
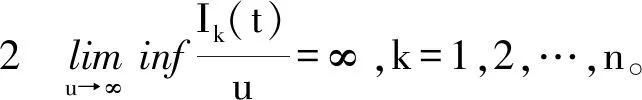
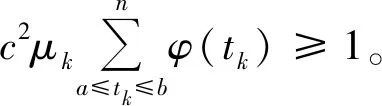
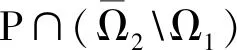
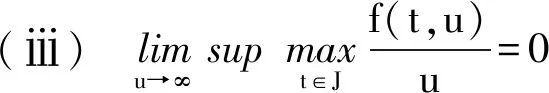
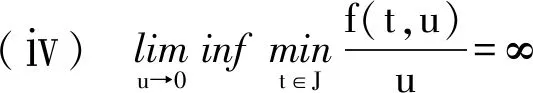


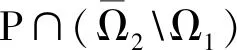
3 应用