可调节相关峰参数的脉冲检测分选算法

赵地， 邓中亮， 杨智勇

(1. 北京邮电大学 智能通信、导航与微纳系统实验室，北京 100876；2.中国电子科技集团公司 第五十四研究所，河北,石家庄 050081；3.重庆工程职业技术学院 信息工程学院，重庆 402260)

塔康(TACAN)是一种为飞机提供方位和斜距导航信息的近程极坐标式无线电导航系统. 它的方位信号由基准信号和包络信号组成，基准信号由固定编码特征的视频编码脉冲序列组成[1]. 视频编码脉冲主要由主基准脉冲和辅基准脉冲组成. 塔康系统有不同的工作模式[2]，不同的工作模式具有不同的脉冲序列编码特征. X模式下的主基准脉冲是脉冲对编码序列，脉内时间间隔是12 μs，脉冲对时间间隔是18 μs；Y模式下则都是30 μs. X、Y模式下的辅基准脉冲是脉冲时间间隔分别为12，15 μs的连续脉冲序列. 基准脉冲序列的检测精度直接影响着塔康系统的定位精度.

然而在实际环境中，由于受飞机与信标台之间的相对运动、大气云层的反射以及大气湍流层的散射影响，无线传输信道的特性会发生改变，比如多普勒频移效应、传输损耗、多径时延等，这些因素无疑会恶化无线传输信道的信噪比；同时，外界环境中存在的其它交叉频带信号如UWB信号、工作在L5频段和E5频段的导航信号等[3-6]都会对塔康信号的接收造成一定干扰，进而影响到视频编码脉冲的检测.

近些年来，国内外研究的重点主要集中在时域的脉冲包络检测、时-频域的脉冲干扰消隐等方面. 常用的方法是采用曲线拟合和相关接收的方法对塔康系统的输出参数进行估计[7]，或者利用滑动窗的时域滤波、峰值检测方法对方位基准信号进行检测[8]，这些算法都是采用单脉冲作为匹配滤波的参考信号，只对视频编码脉冲的PTOA进行检测，并没有结合不同工作模式下的PRI特征信息. 在干扰信号的抑制方面，目前较为理想的方法是基于时-频域的语图谱消隐技术[9]. 另外，通过信号的统计特性确定消隐门限，利用时域脉冲消隐技术[2]和频域脉冲消隐技术[9]也是一种简单而行之有效的抑制干扰脉冲的方法. 文献[4, 10]提出一种基于以上两种技术的混合消隐技术，该方法主要采用时-频域两级检测. 这种方法虽然有效，但时域与频域的两次变换增加了算法复杂度，而且频域陷波需要对干扰信号频率进行估计. 对于分布式干扰源而言，多目标的参数估计会使算法计算量大大增加.

本文提出一种可调节PRI参数基于相关峰峰值位置检测的脉冲分选算法，主要通过PTOA检测、脉冲干扰消隐处理、脉冲对分选等处理过程，获得当前工作模式下符合PRI特征信息的基准脉冲序列，为飞机定位导航提供数据支持.

1 可调参数的互相关滤波检测分选算法

该算法利用脉冲间隔可调节的包含PTOA和PRI特征信息的脉冲对作为匹配滤波的参考信号，根据信号相关滤波的输出模型建立一个目标优化函数，构建一个负定型的互相关检测矩阵，通过对检测矩阵中相关信号相邻峰值位置的检测，滤除当前工作模式下不符合PRI特征信息的脉冲序列以及信号噪声.对于脉冲干扰信号，根据无线信道的传输模型分析干扰信号的中断概率，推导出脉冲干扰信号的消隐门限，采用脉冲消隐技术滤除检测矩阵中的干扰信号. 最后，在脉冲序列PRI量化的基础上利用循环队列对基准脉冲序列进行分选，得到主、辅基准脉冲序列.

1.1 信号模型

塔康系统中高斯脉冲信号可表示为G(t)=Ae-αt2. 一个脉冲时间间隔为D的视频编码脉冲对信号[5]可表示为

s(t)=Ae-αt2+Ae-α(t-D)2.

(1)

式中α为脉冲宽度调整参数. 取该信号作为互相关滤波的参考信号，通过调节参数D可以实现不同工作模式下视频编码脉冲对的检测，在塔康系统中主要是通过调节PRI参数来实现.

在一个理想时不变无线传输信道中，接收到的塔康信号可以表示为

x(t)=u(t)+i(t)+n(t).

(2)

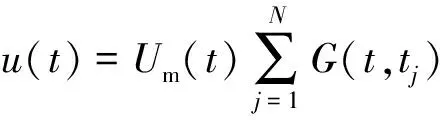
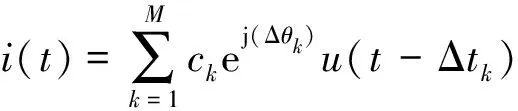
n(t)为加性噪声且与x(t)信号分量u(t)、i(t)不相关.

某一时刻tj互相关滤波输出为

(3)

以时刻tj作为视频编码脉冲信号的时间参考点，通过变量τ可以得到视频编码脉冲的PTOA信息.

1.2 PTOA检测

互相关函数中的峰值位置确定了视频编码脉冲的PTOA信息，时标间隔为D的一对相关峰值可以确定一对待检测的视频脉冲.

由式(1)，假设s1(t)=Ae-αt2，s2(t)=Ae-α(t-D)2，用脉冲对信号s(t)和接收到的信号x(t)进行互相关，可以得到信号x(t)与s(t)的相关表达式为

Rxs(tj,τ)=Ruis1(tj,τ)+Ruis2(tj,τ)+Rsn(tj,τ).

(4)

当加性噪声为理想非相关的高斯白噪声时，Rsn(tj,τ)=0. 那么式(4)则反映了参考信号与塔康视频编码信号、参考信号与干扰信号的互相关. 对式(4)中前两项分解得到

Ruis1(tj,τ)=Rus1(tj,τ)+Ris1(tj,τ),

(5)

Ruis2(tj,τ)=Rus2(tj,τ)+Ris2(tj,τ).

(6)

式中：Rus1(tj,τ)、Rus2(tj,τ)分别为参考脉冲信号与视频编码信号的互相关项；Ris1(tj,τ)、Ris2(tj,τ)分别为脉冲参考信号与衰落效应引起的干扰信号的互相关项. 各个相关子项可以表示为

(7)

(8)

(9)

Ris2(tj,τ)=

(10)

式中：F-1(·)为傅里叶逆变换算子；G(w)为高斯脉冲调制信号G(t)的傅里叶变换，其中

(11)

当两个相关项Ruis1(τ)和Ruis2(τ)满足如下关系：

(12)

它们在τ、τ-D时刻分别存在相关函数极大值. 令τ1=τ、τ2=τ-D，由式(12)可得到目标函数：

L(tj,τ1,τ2,λ)=Ruis1(tj,τ1)+

Ruis2(tj,τ2)+λ(τ1-τ2-D).

(13)

其中λ为拉格朗日乘子. 由式(13)可构造关于向量T=[τ1τ2]的埃尔米特检测矩阵H，它是一个二阶偏导矩阵，表征接收信号与参考信号之间的相关关系，可表示为

(14)

式(14)进一步可分解为

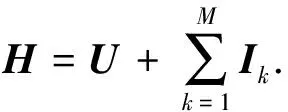
(15)

其中矩阵U是期望信号检测矩阵. 它是参考信号与视频编码信号相关函数的二阶偏导矩阵，矩阵U表示为

(16)

矩阵Ik(k=1,2,…,M)为干扰信号检测矩阵. 它是参考信号与第k个干扰信号相关函数的二阶偏导矩阵，可表示为

(17)

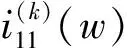
(18)

式中Δθtk=Δθk/w是多普勒频移引起的时延. 由式(16)、(17)和(18)知道，矩阵H可分解成一个期望信号检测矩阵U和M个干扰分量检测矩阵I1，I2，…,IM. 矩阵U和Ik(k=1,2,…,M)都是对角线上元素为负的实对称矩阵，由此可知H是关于T=[τ1τ2]的负定型矩阵，那么峰值位置的检测问题就转换为函数的局部极大值问题. 求解相关检测矩阵H的零点就可以得到相关峰峰值位置. 相关峰值点的时刻所对应的时间延迟点就是接收信号与参考信号的时间对齐的时刻. 如果以tj时刻作为时间参考点，在(0,D)和(tk,tk+D)(tk=Δtk+Δθtk,k=1,2,…,M)这些时间延迟点的位置，检测矩阵中的相关函数会出现一对峰值时间间隔符合PRI特征信息(PRI=D)的相关峰，它们的峰值功率分别为

Pcor(T)=

(19)

根据峰值位置，可以得到塔康视频编码脉冲的PTOA的信息.

1.3 脉冲消隐

从式(19)可以看到干扰信号检测矩阵的相关峰的位置时标，并不是需要的检测信息，它们主要是由多普勒频移、传输损耗以及多径传播时延等因素造成的.

无线传输信道中的多径传播一般服从Rayleigh分布，这里不考虑发射天线和接收天线的增益，只考虑空间链路损耗.

对于时域脉冲消隐而言，设置一个相关门限Vth，使得接收信号场强r满足中断概率条件，即P(r≤Vth)=x%，保证将接收机接收到的因衰落效应引起的干扰信号的概率降低到x%，此时所需要的最小门限值Vth就是需要的消隐门限. 根据Rayleigh分布特征，可以得到

(20)

式中：σ为信号功率的均方根值.

对于频域消隐而言，通过时频分析估计干扰信号频率，采用频域陷波方法对干扰进行抑制. 采用该方法对一段基带信号中的干扰信号进行消隐处理，持续时间为2 ms. 得到处理前后的效果对比图，处理结果如图1所示.

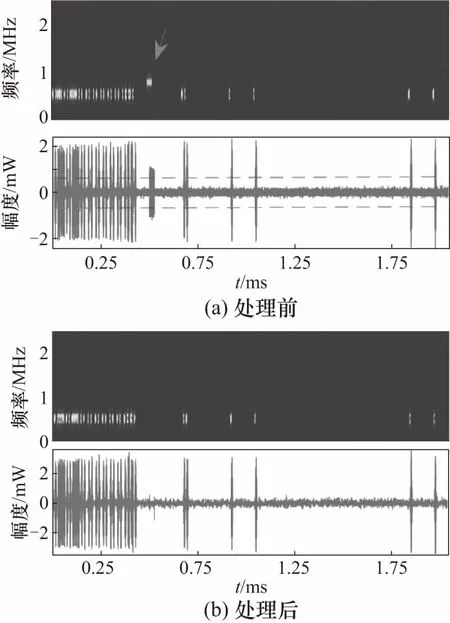
图1 脉冲干扰消隐前后对比Fig.1 Comparison before and after pulsed interference blanking

1.4 脉冲对分选

塔康系统中方位基准信号是具有固定编码特征的视频编码脉冲序列，这里以X模式为例对脉冲对分选处理流程进行阐述. 在X模式下，信标台发射主基准脉冲序列发射周期为66.7 ms，辅基准脉冲发射周期为7.41 ms，分别记为T1、T2. 如果接收机在时刻tj接收到信号x(tj)，持续时间为Ts，在下一时刻tj+1接收到的信号为x(tj+1). 那么在持续时间Ts-[Ts/T1]T1和Ts-[Ts/T2]T2内无法得到一个完整周期的脉冲对序列. 由于脉冲序列信息不完整性会造成脉冲序列对的丢失. 为解决这一问题，运用循环队列的思想对检测到的脉冲序列进行量化分选. 在x(tj+1)时刻保留上一时刻x(tj)的不完整信息，可以保证脉冲序列周期的完整性；避免x(tj+1)时刻输入的信息“溢出”队列而导致上一时刻x(tj)的信息丢失.

结合X模式下视频编码脉冲序列的PTOA和PRI特征信息，图2给出了循环队列脉冲对分选的处理流程.

其处理过程如下：

步骤1 检测符合特征信息的脉冲序列；

步骤2 确定脉冲在算法循环队列的起始和终止位置；

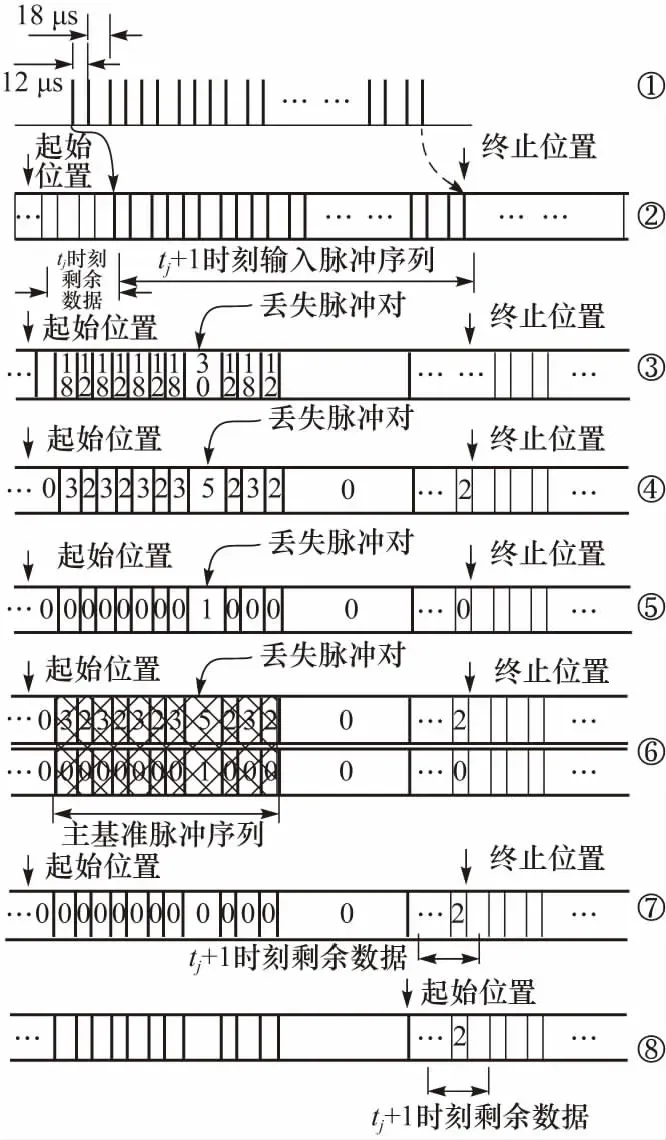
图2 脉冲分选处理流程Fig.2 Pulse sorting processing flow

步骤3 确定脉冲对时间间隔；

步骤4 PRI特征信息量化编码；

一是坚持竞争立项，把“要我干”变成“我要干”。按照公平、公正、公开的原则，从2010年开始对中央小农水重点县实行竞争立项。2013年，湖北省还对中央财政小农水重点县竞争立项过程实行电视直播，现场评分并公布成绩，有效避免了人为因素和暗箱操作。

步骤5 脉间丢失脉冲数量化编码；

步骤6 主基准脉冲序列判决；

步骤7 记录下脉冲的有效位置，输出结果清循环队列，计算将留到下一次参与搜索的剩余序列长度；

步骤8 搜索辅基准脉冲序列，得到辅基准脉冲可能剩余序列长度，与步骤7比较，偏移循环队列起始位置.

2 实验仿真及结果分析

对一段持续时间400 μs的塔康视频编码信号(包含X模式下的主基准脉冲序列)，用本文算法仿真，检测分选的结果如图3所示.

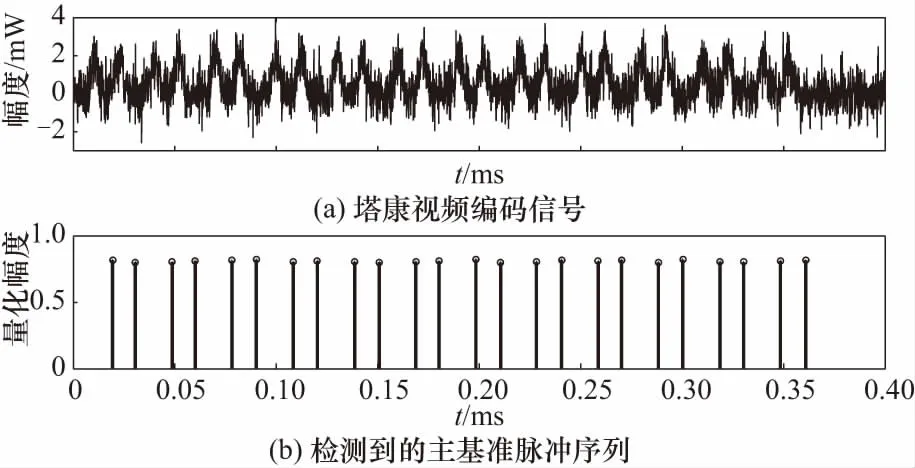
图3 主基准脉冲检测分选结果Fig.3 Sorting result of main benchmark pulse sequences detection

2.1 算法对信噪比的改善情况分析

用本文算法与采用滑动滤波的峰值检测算法对基带信号中的脉冲序列进行处理. 图4给出了两种算法对含有加性噪声的塔康视频编码信号在时域及相关域的处理结果.

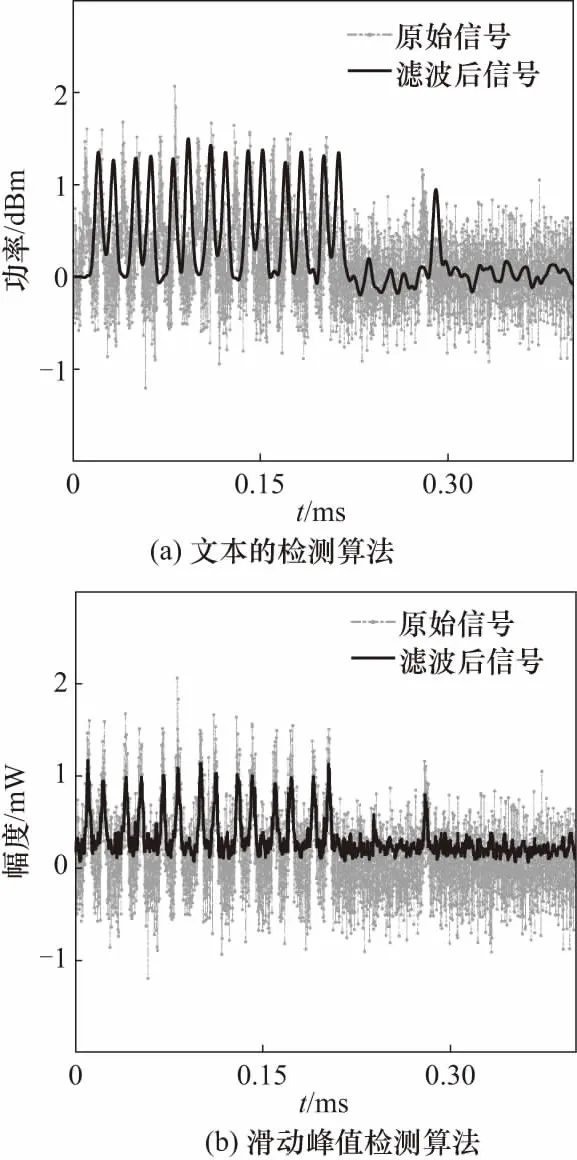
图4 脉冲检测效果对比Fig.4 Comparison of pulse detection effect

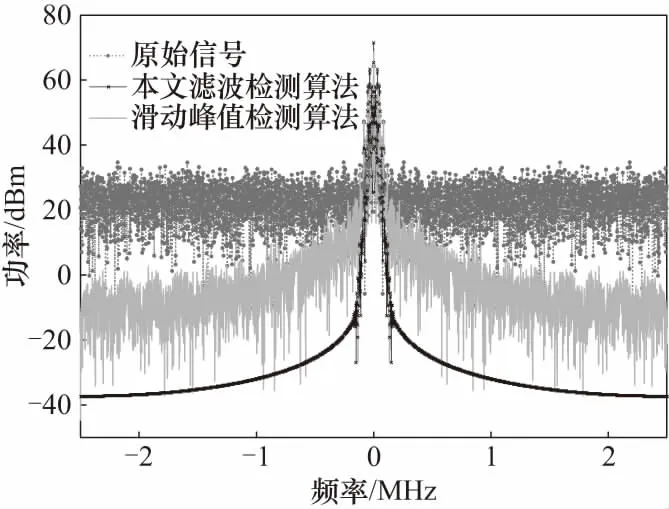
图5 脉冲检测信噪比Fig.5 Comparison of signal-to-noise ratio in pulse detection

可以看到，采用相关的处理方法，信号的信噪比有了明显的改善. 在理想的仿真环境中，如果接收机的频率响应是恒定的，采用本文的检测算法比滑动峰值检测算法有将近20 dB的信噪比改善. 在衰落的信道环境下，有效地提高低信噪比下视频编码脉冲信号的检测性能.

2.2 算法的检测误差及复杂度分析

通过对信噪比为0～35 dB的视频编码脉冲信号仿真，得到不同信噪比下的PTOA估计误差的性能曲线，如图6所示.

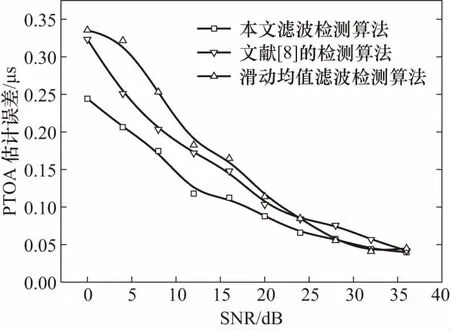
图6 PTOA检测性能曲线Fig.6 Performance curve of PTOA detection

由图6看到信号信噪比越低，这几种算法的性能差异就越明显. 对本文检测算法、文献[8]的滑动峰值包络检测算法以及滑动窗均值滤波检测算法的PTOA检测误差和时间复杂度进行分析. 表1给出了上述几种算法的PTOA检测误差和时间复杂度(N为待检测数据长度，K为输入滤波器长度).

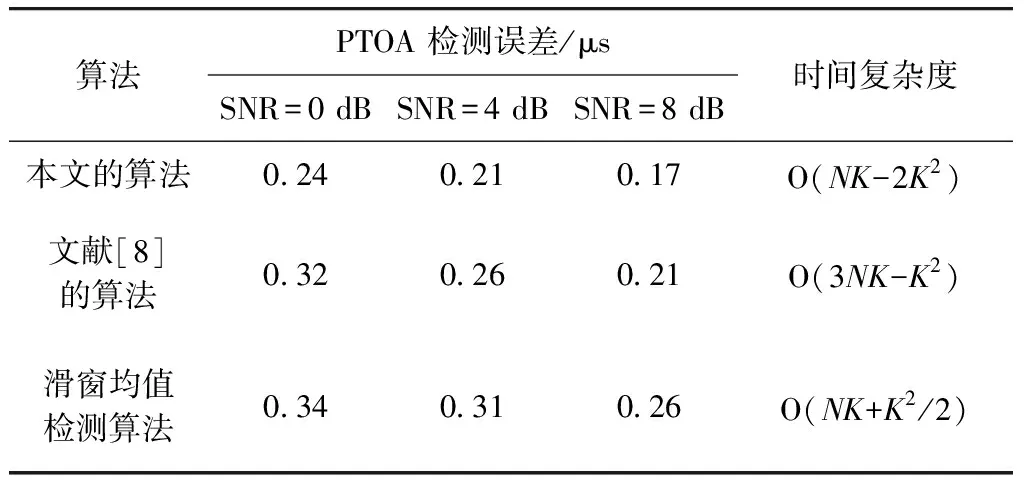
表1 PTOA检测误差和复杂度比较表

当SNR分别为0,4和8 dB时，本文算法的PTOA检测的标准偏差都比其他算法小，SNR越低，这种优势就越明显. SNR≤8 dB时本文检测算法的估计误差至少优于其他算法0.09 μs. SNR为25 dB时，本文算法对PTOA估计误差在0.07 μs，优于其他的算法0.02 μs；当SNR=4 dB时，这种优势会提高到0.10 μs. 因此，在信噪比较低的情况下，本文算法较其他算法具有良好的检测性能.

上述几种算法的复杂度主要由数据长度和匹配滤波或滑动窗长度决定(其他算法不涉及到脉冲分选). 滑动峰值滤波检测算法[8]采用滑动峰值检测，检测步进为一个采样点，通过比较窗口内数据与窗口内首尾两个采样点的数值获得脉冲的预判门限，然后对数据作平滑累加运算. 在待检测数据长度一定的情况下，其运算时间函数为(N-K+1)(K-2)+N(2K-1)；如果采用滑动窗均值滤波检测，然后直接与预判门限比较，其时间函数为(N-K+1)K+K(K+1)/2；而本文算法的时间函数为2K(N-2K+1). 就其时间函数而言，由于滑动峰值滤波检测算法涉及到平滑累积，其算法复杂度最高；滑动窗均值滤波后直接参与门限判决，其复杂度次之，但是从图6可以看到其检测误差也最大；本文的检测算法复杂度最低，而且从表1中结论可以看到其对信噪比的改善情况要远远好于滑动滤波，这也大大提高了低信噪比下的PTOA的检测能力.

2.3 PRI容差的影响分析

由于信号传输路径造成源信号的时延扩展，载波与接收机变频频率的偏差会导致接收到的脉冲特性信息产生改变，如脉冲形状畸变等，因此需要设置合理的PRI检测容差. 图7给出了不同信噪比下检测率与PRI容差之间的关系曲线. 随着容差的增大，检测率也随之增加. 塔康视频编码脉冲对的单脉冲的宽度为(3.5±0.5) μs，脉间间隔为(12±0.1) μs. 理论上最大允许容差为1.2 μs.

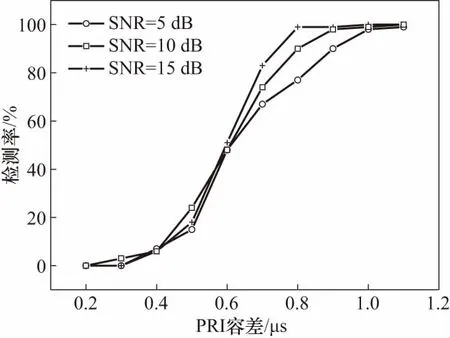
图7 不同SNR下检测率随PRI容差的变化关系Fig.7 Relationship between detection-ratio and PRI tolerance under different SNR circumstances

PRI容差设置过小，相应的PTOA检测误差也必须要尽可能小，然而这样的参数设置，有可能会造成脉冲检测失败；如果PRI容差设置过大，虽然对PTOA的检测误差要求降低了，错误脉冲的检测概率也大大地增加了. 信噪比低时，为保证分选算法需要的基本脉冲个数，可以适当增大PRI容差范围；信噪比高时，可以适当减小PRI容差范围. 图8给出了PRI允许容差为0.85 μs时脉冲检测率与信噪比之间的变化关系. 当SNR为5 dB时，利用本文的算法仍有80%的正确检测率.

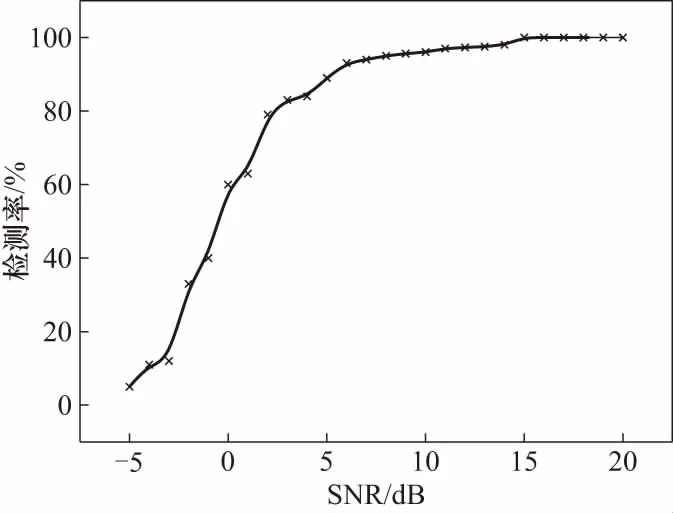
图8 PRI容差为0.85 μs时检测率随SNR的变化关系Fig.8 Relationship between detection-ratio and PRI tolerance with PRI=0.85 μs

3 结束语

根据塔康信号的编码特征，调整PRI参数可以实现不同工作模式下的基准脉冲序列的检测分选，算法的检测性能不会因为工作模式不同而有所差异. 本文算法互相关滤波后的数据保留了塔康信号编码的特征信息，选择合适的时间参考点，就可以实现符合PRI特征信息的基准脉冲序列的检测，通过仿真看出，本文的算法比传统的滤波检测算法在相同信噪比下的PTOA估计误差小，根据信噪比自主设置PRI容差可以得到理想的检测效果.