无源互调干扰的二维时延自适应估计算法

韩航程， 程志恒， 孙灿灿， 田露

(北京理工大学 信息与电子学院，北京 100081)

当两个或多个载波同时经过非线性器件时，由发射系统中各种无源部件(如天线、双工器等)的非线性特性引起的互调现象称为无源互调(passive intermodulation，PIM)[1-2]. 当这些杂散的PIM信号落在接收频段内，且功率超过系统中的有用信号的最小幅度，就会对无线通信、卫星通信、舰船通信等通信系统的正常工作产生严重影响[3].

自20世纪60年代，针对PIM问题的研究报告首次发表以来，不少学者开始了对PIM产生机理、测试方法、预测估计和抑制手段的研究[4]. 准确的预测和估计可帮助判断PIM对通信系统影响，并为抑制方案建立基础. 早期对PIM信号的估计是采用幂级数方法利用低阶PIM测试结果估计较高阶PIM电平[5]. 但该方法仅能估计出PIM信号功率，无法估计出宽带信号激励下PIM信号的时域波形. 2011年，Edward A. Keehr和Ali Hajimiri[6]提出了一种高阶互调产物的模拟重建方法. 该方法通过对2阶和3阶互调产物的组合计算来估计高阶互调分量. 同年9月，爱立信公司申请发明专利，提出了一种无源互调干扰的动态消除方法，首先利用导频估计无源互调效应的非线性参数，再利用所得参数估计PIM信号，进而实现消除[7]. 已有的PIM信号估计方法多采用幂级数模型描述无源互调效应的非线性，未考虑无源互调产物的记忆效应. 直到2014年9月，华为技术有限公司申请发明专利，提出了一种射频模块的无源互调干扰抵消方法[8]. 该方法中对无源互调的估计考虑了记忆效应，采用简化的Volterra级数模型描述无源器件的非线性.

以上相关研究均未考虑激励无源互调产生的两路或多路载波间的相对时延. 本文充分考虑PIM信号估计的实时性和算法的硬件可实现性，提出了一种可用于PIM干扰数字对消的二维时延估计算法. 经过二维时延估计后，可对PIM信号实现更好的估计效果.

1 数学模型

为便于理论分析，简化模型，假定产生无源互调干扰的激励信号x(t)由两个等功率无相对时延的QPSK信号S1(t)、S2(t)组成. 实际上，在实际系统中，两路激励信号S1(t)、S2(t)的二者之间存在相对时延，并且该相对时延具有时变性. 以信号S1(t)的时间为基准，即双载波时延表现在信号S2(t)上，则激励信号可表示为

x(t)=S1(t)+S2(t+τ1)=

I1(t)cos[ω1t+φ1]-Q1(t)sin[ω1t+φ1]+

I2(t+τ1)cos[ω2(t+τ1)+φ2]-Q2(t+τ1)×

sin[ω2(t+τ1)+φ2].

(1)

采用幂级数模型对PIM信号进行建模，则由式(1)所示信号激励产生的n阶PIM产物可表示为

Sn(t)=anxn(t)=an[S1(t)+S2(t+τ1)]n=

Q1(t)sin[ω1t+φ1]}n-k×{I2(t+τ1)×

cos[ω2(t+τ1)+φ1]-Q2(t+τ1)×

sin[ω2(t+τ1)+φ1]}k.

(2)

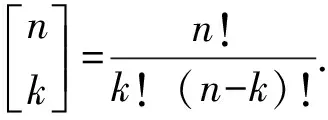
Sn(t)中还包含了未落入接收频带的信号，本文中只关注载波频率为ωc的某一特定阶次无源互调信号，根据积化和差公式，得到PIM干扰信号表示为

(3)

式中φ=pφ1+qφ2.

当(k+l)为奇数时，上式可转化为正弦形式，当(k+l)为偶数时，上式可转化为余弦形式，故式(3)可以进一步简化为

SPim(t)=IPim(t)cos(ωct+φ)+

QPim(t)sin(ωct+φ).

(4)

式中I、Q两路基带信号IPim、QPim可根据双载波信号的基带数据I1(t)、I2(t)、Q1(t)、Q2(t)计算得出.

式(4)具有类似QPSK信号的表示形式. 由此可得，两路QPSK信号激励产生的无源互调干扰信号同样具有QPSK的信号特性.

图1所示为不同双载波时延值时，无源互调信号的时域波形. 仿真条件：双载波基带数据均为1111000011110000……，过采样倍数为160，调制方式为BPSK，双载波时延值τd为采样点数. 由图1可见，在双载波数据一定时，相对时延τ1直接影响PIM信号的时域波形.

此外，基于自适应滤波的无源互调干扰数字域对消技术，必须在自适应滤波之前使PIM信号的估计值SPim与实际接收的PIM信号SPim对齐，即估计二者间的时延τ2并进行补偿. 图2显示了PIM信号的估计信号SPim与实际接收的PIM信号SPim的时域波形图，二者间存在相对时延.

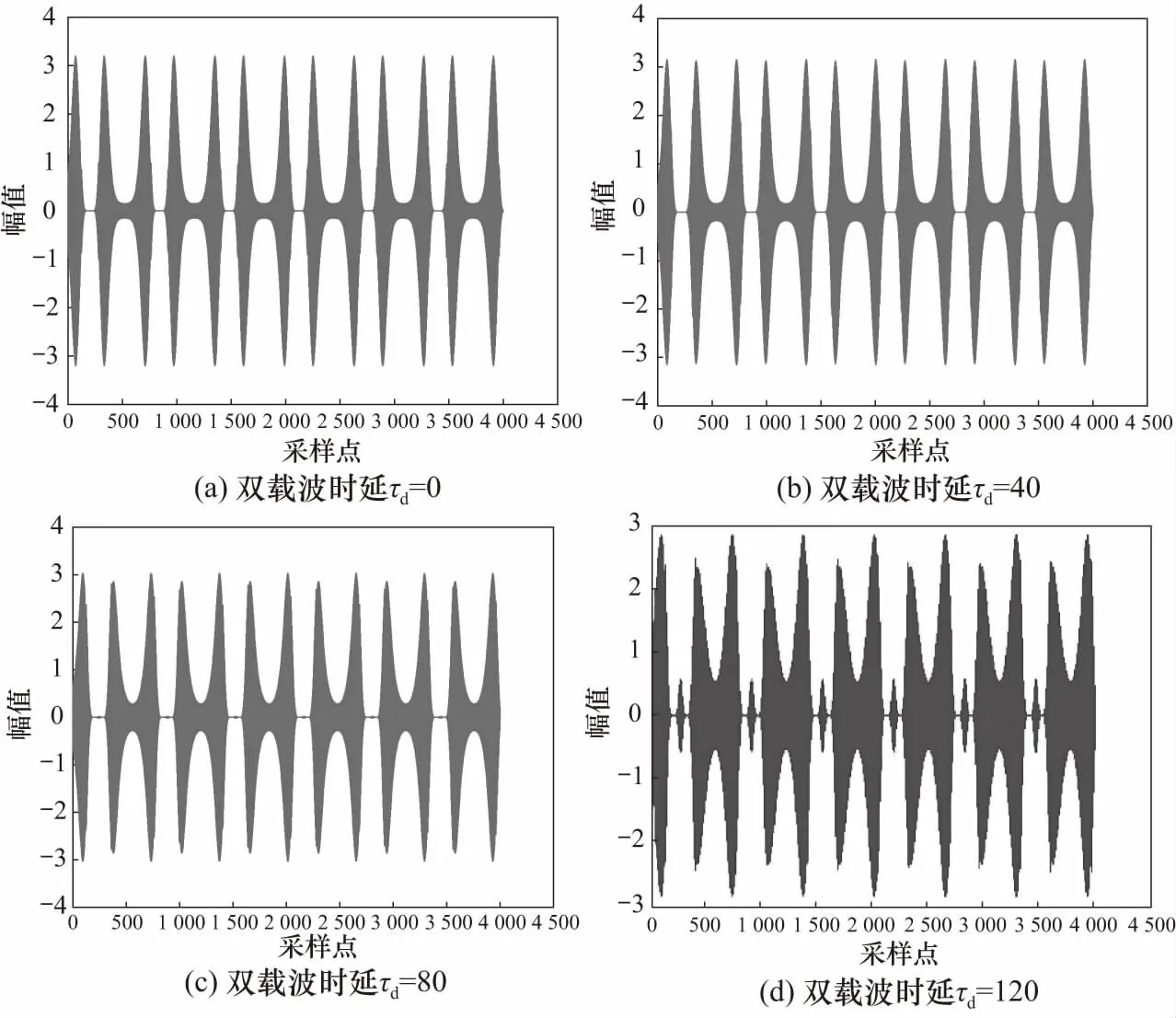
图1 不同双载波时延下的PIM信号时域波形Fig.1 Time domain waveform of PIM signal under different carrier delay

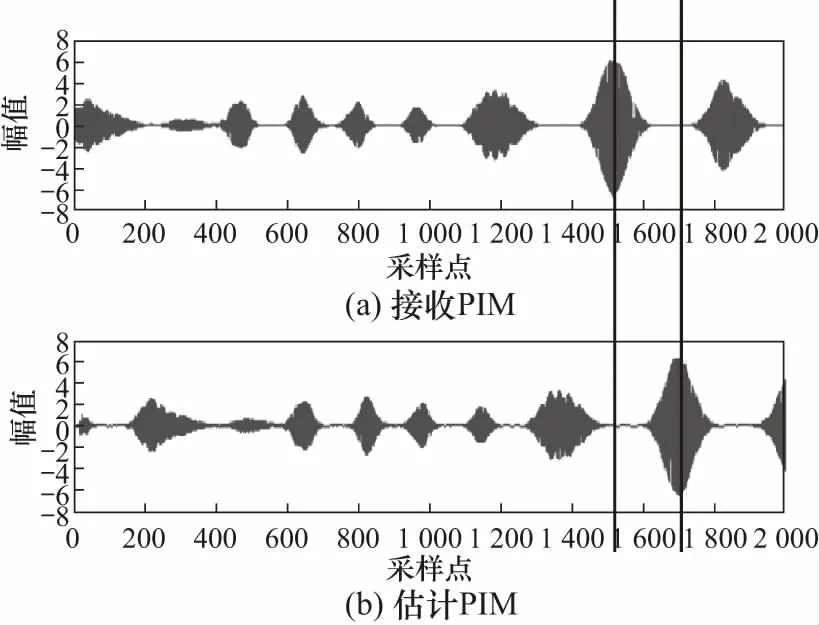
图2 接收PIM与估计PIM时延Fig.2 Time delay between receive and estimate PIM signal

2 二维时延估计

由以上分析和仿真可知，系统中存在两个时延信号：双载波信号的相对时延τ1；PIM信号的估计值SPim与实际接收的PIM信号SPim之间的时延τ2. 时延估计利用PIM信号估计值SPim与实际接收的PIM信号SPim之间的相关性，取二者的4路相关值的平方和R2，R2峰值的坐标表征了两种时延值. 在双载波时延值一定时，R2可表示为

(5)

式中：

(6)

(7)

(8)

(9)

式中：I(k)和Q(k)为接收信号的基带信号；IPim(k)和QPim(k)为PIM信号估计值SPim的基带信号.

图3显示了二维时延下R2的值，相关长度为2 048采样点，双载波时延值搜索范围为±140采样点. 设置双载波信号时延τ1=80，干扰信号时延τ2=60，单位为采样点数，不考虑频偏和相偏. 图3(a)中相关峰坐标为(224,1 031)，折合为双载波信号时延τ1=83个采样点，干扰信号时延τ2=56个采样点，相关峰的坐标在一定误差范围内代表了两种时延值. 图3(b)中“投影相关峰”为图(a)在双载波时延方向上的投影，“切面相关峰”为图3(a)在干扰信号时延为定值(1 031)时的峰值，由此可见，两种时延相互关联，必须采用二维的时延估计方法才能准确估得τ1、τ2. 本文根据相关值R2提出一种易于硬件实现的二维时延估计算法，并在原理样机中实现.

二维时延估计及其补偿算法的基本思路如图4所示具有反馈回路.

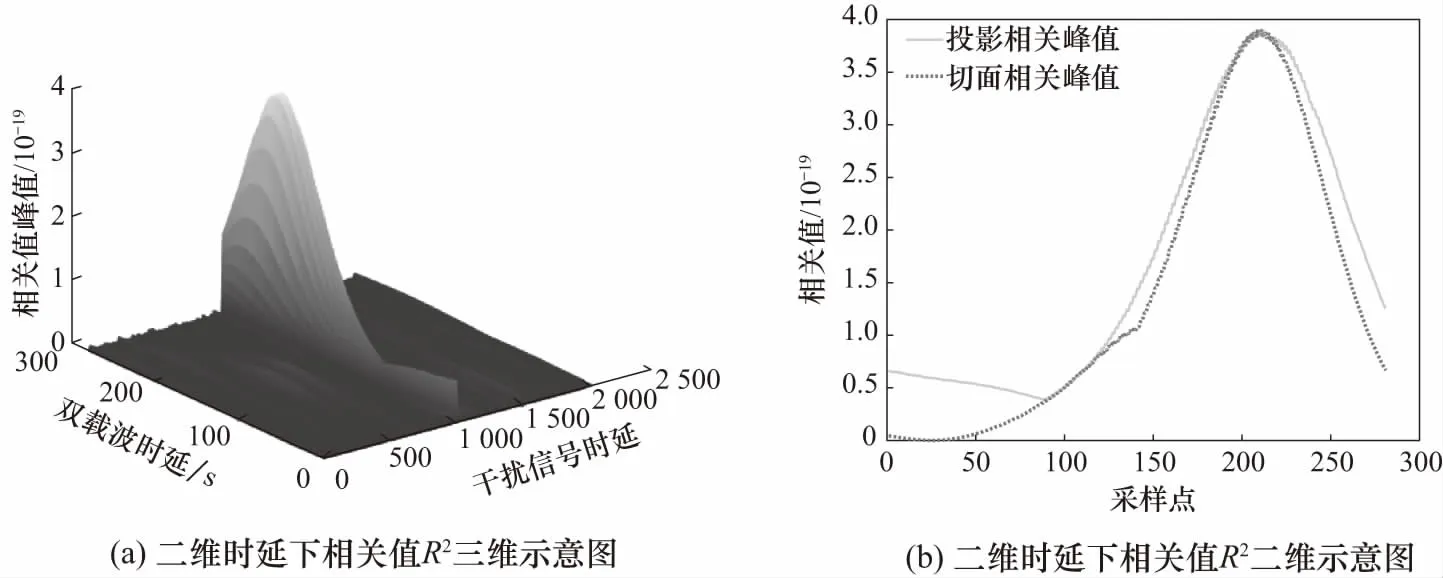
图3 二维时延下相关值R2Fig.3 Correlation value of two dimensional time delay

图4 二维时延估计算法示意图Fig.4 Schematic diagram of two dimensional time delay estimation algorithm

在实际中，双载波时延是在一定范围内的，即|τ1|<τ1max，τ1max是可能存在的最大双载波时延. 为得到适用于硬件实现的算法，本文对3种不同的搜索方法进行了性能仿真与对比. 仿真设定双载波时延τ1=80，PIM信号时延τ2=60，单位为采样点.

① 二分法搜索算法：二分法搜索算法每次仅输出一个搜索时延值τ′1，每次搜索到的相关峰值与最大相关峰值比较大小，确定下一时刻要检测的时延值.

② 快速二分法搜索算法：快速二分法搜索算法每次输出两个搜索时延值τ′1in、τ′1ed，每次搜索到的两个相关峰值相互比较大小确定下一时刻要检测的时延值.

③ 并行网格搜索算法：并行网格搜索算法每次输出多路搜索时延值，假设为4路并行(R=4)，每次搜索到的R路相关峰值相互比较取最大值，并根据最大值处的时延值和循环次数确定下一时刻要检测的R个时延值.

3 算法仿真与对比

二分法搜索算法性能仿真通过图5和表1可以看出，经过8次检索后，二分法二维时延估计可以有效检索到峰值，最终估得双载波时延为82，此结果在误差范围内.

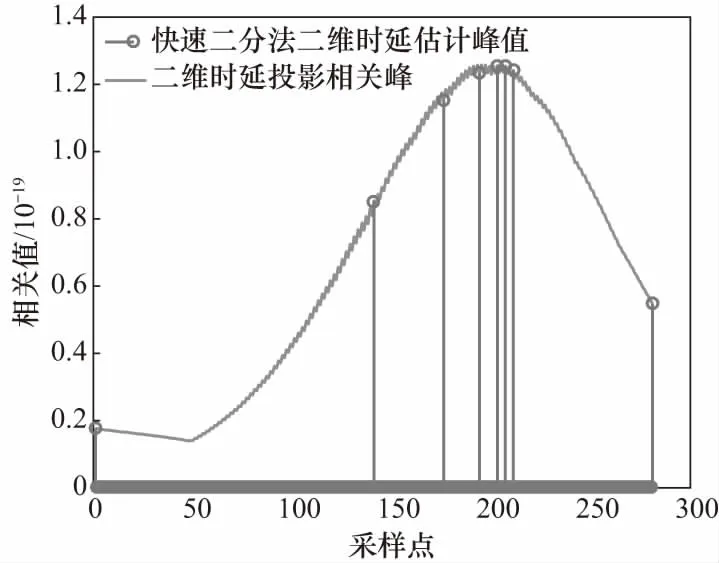
图5 二分法搜索算法峰值搜索示意图Fig.5 Schematic diagram of the binary search algorithm

i12345678τ′1-140140070105887984

快速二分法搜索算法性能仿真如图6 所示，双载波时延搜索过程中间值如表2所示. 可以看出，经过6次检索后，二分法二维时延估计可以有效检索到峰值，最终估得双载波时延为80，此结果在误差范围内.

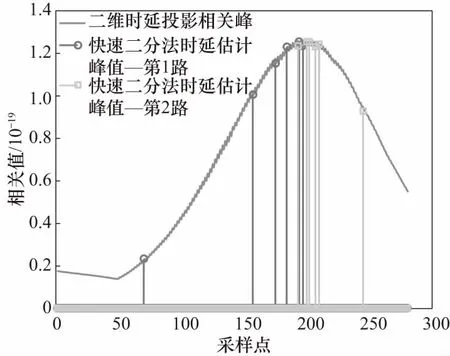
图6 快速二分法搜索算法峰值搜索示意图Fig.6 Schematic diagram of the fast dichotomy algorithm

表2 快速二分法搜索双载波时延过程Tab.2 Dual carrier delay search by fast dichotomy algorithm

并行法估计算法性能仿真如图7 所示，双载波时延搜索过程中间值如表3所示. 可以看出，经过3次检索后，二分法二维时延估计可以有效检索到峰值，最终估得双载波时延为81，此结果在误差范围内.

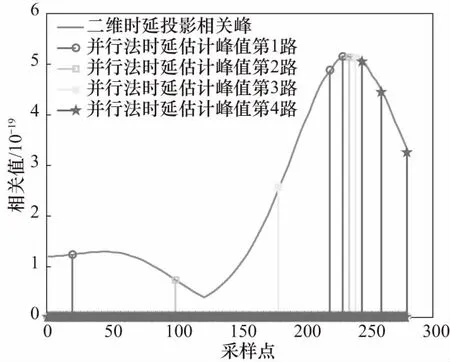
图7 并行搜索算法峰值搜索示意图Fig.7 Schematic diagram of the parallel algorithm

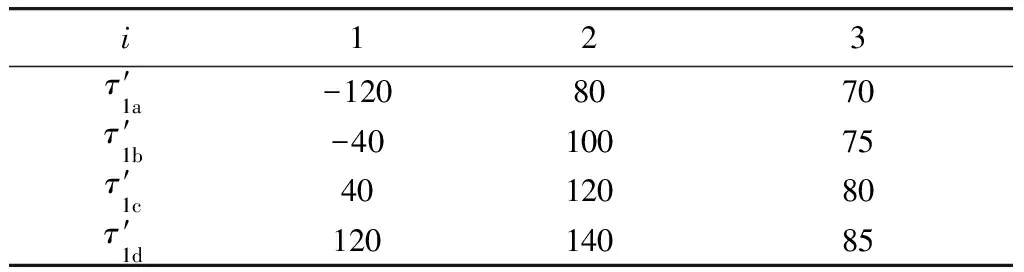
i123τ′1a-1208070τ′1b-4010075τ′1c4012080τ′1d12014085

由以上仿真数据可得以下结论：基于二分法的估计算法复杂度低，资源消耗量最低，但速度相对较慢；基于并行法的估计算法速度最快，循环次数最少但复杂度最高，资源消耗量最大；基于快速二分法的估计算法是二者的折中，相比于并行搜索法，资源消耗量较低，相比于二分法，跟踪速度较快. 表4为3种二维时延估计算法性能对比.

表4 3种二维时延估计算法性能对比

Tab.4 Comparison of three kinds of two-dimension time delay estimation algorithms

算法结构复杂度资源消耗跟踪速度精确度二分法较低较低最慢较低快速二分法较低较低较快较高并行搜索法较高较高最快较高

本文采用基于快速二分法的二维时延估计算法用于PIM干扰信号的自适应对消. 对消效果见图8所示. 仿真证实，PIM时变跟踪模块的加入可有效改善对PIM信号的对消效果.

图8 有无二维时延估计时LMS对消效果Fig.8 Cancellation effects of LMS algorithm with or without two-dimension time delay estimation

4 硬件实现与实测数据

为验证算法的有效性，本文以卫星通信系统为模型搭建硬件验证平台. 验证平台包含下行链路信号中频调制模块、上行链路信号中频调制模块、无源互调干扰效应模拟模块及无源互调干扰对消接收机等组成. 其主要功能如下.

① 模拟卫星上下行链路数据的产生、发送和接收功能.

② 模拟产生无源互调干扰信号的功能，并能够配置PIM信号功率.

③ 无源互调干扰实时抑制的功能.

④ 人机交互界面，可实现操作控制、状态显示、数据处理等功能.

⑤ 上行链路误码率和误帧率测试功能.

主要器件型号与数量如表5所示.

表5 信号处理板主要器件型号与数量

Tab.5 Type and amount of main device of signal processing board

器件名称型号数量/片FPGAXilinx公司Virtex-6系列1模数转换器AD9246(单通道/最高采样率125 MSPS)1AD9640(双通道/中频最高采样频率450 MSPS)1数模转换器AD9781(双通道/最高转换速率500 MSPS)1AD9778(双通道/最高转换速率1 GSPS)1时钟管理芯片AD95122

根据二维时延估计得到的数据对本地重建PIM干扰信号进行修正，修正后的信号送至自适应滤波器. 图9和图10所示为有无二维时延估计和补偿处理情况下自适应滤波效果的chipscope实测数据，设定PIM阶次为7阶. 其中，黑色曲线表示实际接收到的PIM信号，灰色曲线为滤波后的信号，即接收PIM与估计PIM的差值. 图9中灰色曲线最大值与黑色曲线相当，对消效果较差；图10中灰色曲线接近于0，对消效果理想. 可见，PIM时变跟踪模块的加入可有效改善对PIM信号的对消效果.

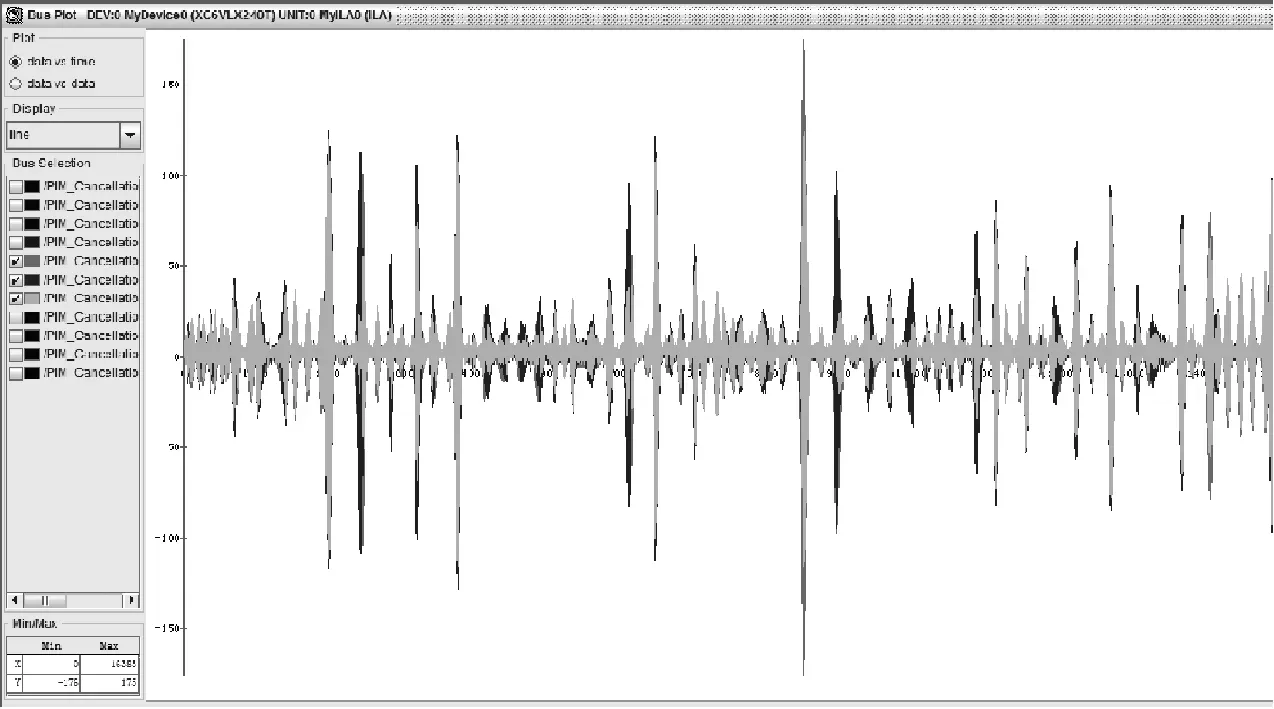
图9 二维时延估计前对消效果Fig.9 Cancellation effect before two-dimension time delay estimation

图10 二维时延估计后对消效果Fig.10 Cancellation effect after two-dimension time delay estimation

5 结束语

提出了适用于PIM干扰自适应对消的二维时延估计算法，对PIM干扰系统中特有的二维时延进行估计与补偿，以使自适应估计模块获得良好的PIM干扰对消效果. 本文对3种不同的二维时延搜索算法进行介绍、仿真及分析. 结合实际应用场景，充分考虑算法复杂度、资源消耗、跟踪速度等性能指标，选择基于快速二分法的二维时延估计算法用于硬件实现. 硬件平台的测试数据验证了二维时延估计算法的有效性. 本文提出的算法对无源互调干扰的数字对消算法具有重要意义.