符号执行中的约束求解问题研究进展

邹权臣， 吴润浦， 马金鑫， 王欣， 辛伟， 侯长玉， 李美聪

(1.中国信息安全测评中心，北京 100085； 2. 360安全研究院，北京 100016；3. 北京中测安华科技有限公司，北京 100085)

在符号执行中，对路径约束条件的可达性判定以及生成实际的测试输入都严重依赖于可满足模理论(SMT)求解器. 虽然当前的SMT求解器已经能够处理较大型的约束，但对复杂约束的处理能力不足，而且随着约束体积的增大，求解的效率会越显低下；这使得约束求解问题成为了符号执行中的主要瓶颈问题之一.

约束求解问题的研究关系着符号执行的效率和性能，影响着符号执行应用到大型应用程序中. 同时，这方面的研究对漏洞挖掘、自动化网络攻防等领域也具有非常重要的意义.

本文介绍了符号执行和约束求解的基本概念，并分析了符号执行中约束求解问题的由来，对近年来的约束求解问题研究进展进行了归类，展望和总结.

1 符号执行与约束求解

1.1 SMT理论

可满足模理论(satisfiability modulo theories， SMT)主要用于自动化演绎的研究方法，是为了检验基于逻辑理论的一阶谓词公式的可满足性而提出[1]，已经被广泛应用于模型检测、自动化测试生成等计算机科学领域. 典型的应用理论主要包括了各种形式的算术运算、数组、有限集、比特向量、代数数据类型(algebraic datatypes)、字符串、浮点数以及各种理论的结合等.

相对于SAT(boolean satisfiability problem)求解器，SMT求解器不仅仅支持布尔运算符，而且在使用SMT求解器解决问题的时候不需要把问题转化成复杂的CNF(conjunctive normal form)范式，能大幅度简化求解问题.

当前性能比较好的SMT求解器有CVC[2]、Z3[3]、STP[4]、YICES[5]、MathSat[6]等，其性能对比如表1所示. 其中Z3求解器在每年的SMT求解器竞赛[7]中各方面的性能都名列前茅，通过内置理论对一阶逻辑多种排列进行可满足性校验，Z3当前支持如位向量、实数和整形运算(有限支持非线性运算)、阵列、函数和谓词符号、元组、枚举类型和代数(递归)数据类型等理论.

表1 常用SMT求解器对比

SMT理论和技术的发展是驱动符号执行应用于大型程序最主要的动力之一，同时当前SMT求解器能力和性能的不足也制约着符号执行应用的发展.

1.2 符号执行中的约束求解问题

符号执行在20世纪70年代被提出[8-12]，是一种能够系统性探索程序执行路径的程序分析技术，通过对程序执行过程中的被污染的分支条件及相关变量的收集、翻译、取反，生成新的路径约束条件，然后使用SMT求解器进行求解,判断路径的可达性以及生成相应的测试输入. 通过这种方式产生的路径与测试输入之间的关系是一一对应的，能够避免冗余测试输入的产生，并有效解决模糊测试中冗余测试用例过多导致的代码覆盖率低的问题.

自符号执行特别是动态符号执行[13-14]技术提出以来，目前已经广泛应用于程序分析的各个领域，如自动化测试输入生成、漏洞挖掘、漏洞利用自动生成、签名生成、协议逆向工程等. 很多相关的项目和工具也已经被应用到实际的漏洞挖掘当中，如angr[15-17]、KLEE[18]、Bitblaze[19]、Mayhem[20]、SAGE[21-23]、S2E[24]等. 其中微软开发的符号执行工具SAGE已经被应用到了微软内部的日常开发安全测试中，每天有上百台机器同时在运行此工具，并已声称发现了Windows 7系统中1/3的漏洞[23]. MergePoint已经在Debian系统下发现上千个bug，其中有上百个被证实是安全漏洞[25]. 另外，在2016年8月份由美国国防部高级研究计划局(DARPA)举办的全自动化的网络安全挑战赛(cyber grand challenge)[26]决赛中，大部分团队都采用了符号执行技术对测试集进行漏洞挖掘. 符号执行技术将成为未来网络攻防自动化和智能化的重要技术基础.

虽然符号执行相比其他程序测试和分析技术有诸多的优势，在科研和工业领域也取得了长足的进展，但就当前的形势而言，要大规模应用到工业领域，仍然还有很多问题需要解决. 如路径爆炸、约束求解、浮点计算、内存建模、环境交互以及并行计算等问题是符号执行急需解决的问题，这些问题影响着符号执行应用到大型应用程序当中.

约束求解问题是符号执行遇到的主要瓶颈问题之一[27]. 在符号执行中，因为对路径约束条件可达性的判定以及相应路径的测试输入的计算都需要频繁地调用SMT求解器进行求解，而路径的数量关系着对SMT求解的频率，每条路径约束的体积和复杂度影响着单次求解的效率和能力. 目前SMT求解器在能力上对浮点运算和非线性运算的支持并不好，而在求解效率上，虽然每年的SMT求解竞赛一直在促进这方面的研究，但约束求解本身是一个NP完全(NP-complete)问题,在最差的情况下求解NP完全问题的复杂度为指数级，求解器的性能和能力仍然受限于可满足模理论(SMT)的研究进展. 频繁调用加上高的求解难度直接导致约束求解占用了符号执行系统中的大部分资源消耗.

另一方面，近年来也有研究人员采用符号执行辅助模糊测试绕过校验和检验机制[28]或者引导路径探测[29-32]. 如Stephens等[31]采用模糊测试和符号执行交替探索程序执行路径，解决模糊测试陷入代码覆盖率增长慢的情况，这样能引导模糊测试探索到程序更深层次的节点，也能直接避免符号执行可能带来的路径爆炸问题. 但Dolangavitt等[33]文献的实验结果表明，使用符号执行对模糊测试中部分路径约束求解时，仍然有很大一部分路径出现求解失败的情况(Driller实验中有41个测试程序陷入了较浅路径，使用符号执行对其求解时只有13个程序能够生成新的测试输入). 所以基于符号执行增强的模糊测试技术仍然会受限于符号执行中的约束求解问题，符号执行的引入可能会弱化模糊测试本身的可扩展性.

2 研究进展

当前，约束求解遇到的两大问题可归结为求解器求解能力与求解效率问题. 求解能力问题是指求解器对复杂约束条件(如浮点数以及非线性约束)处理能力的不足. 而求解效率问题是指对于含有大量的约束条件的路径约束，求解器的性能会随着约束条件数量的增长而逐渐下降.

针对以上问题，研究人员提出了很多约束求解性能优化措施，主要可分为内部优化和外部优化. 求解器内部优化是指通过优化求解器本身对约束条件处理能力和效率来提高符号执行的性能，虽然近年来这方面的研究已经取得了比较大的突破[34-39]，但仍然严重依赖于可满足模理论以及NP完全问题的研究进展；求解器外部优化主要是指在调用约束求解器对路径约束求解之前的优化，是通过减少甚至避免符号查询的工作来增加符号执行性能的措施. 当前大部分技术都对路径约束进行了启发式处理，如精简约束式尽量减少求解器的求解负担；对求解结果进行缓存和重用，减少调用求解器的次数等. 本文主要关注求解器外部优化处理问题.

对于求解器外部性能优化问题，早期很多的符号执行工具提出了各种切实可行的解决方案. 如CUTE[40-41]、EXE[42]和KLEE[18]提出的一系列如表达式重写、符号值的实际替换、不相关约束的删除以及约束缓存等的措施对路径约束进行精简和结果重用. 近年来，在这方面的研究又有了不小的突破，其中有Memoise[43-44]、Green[45]、GeenTrie[46]以及Recal[47]等，这些工具的提出主要侧重于优化符号执行结果切片、标准化命名、求解结果的缓存、搜索和重用的效率等问题. 这些文献的实验结果表明，符号执行结果的缓存和重复使用能在同一程序的不同路径以及不同程序的不同路径间的约束求解问题上大幅度减少对求解器的调用.

本文对约束求解研究的相关工作进行了梳理归类(如图1所示)，按照约束求解优化措施的实施的阶段(相对于对求解器调用的时机而言)不同，把近年来的相关研究工作大致分为求解前优化、求解时优化以及求解后优化. 下面将对这些约束求解方面的优化技术进行详细介绍.

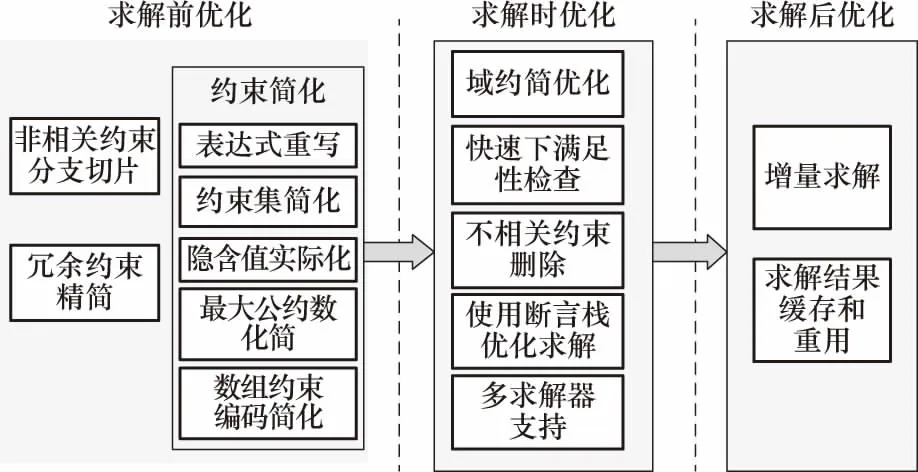
图1 约束求解研究进展Fig.1 Research progress on constraint solving

2.1 求解前优化

求解前优化主要是在调用SMT求解器对路径约束进行求解之前做的一些预处理工作，包括非相关约束分支切片、约束简化以及冗余约束精简等. 这些工作既能减小路径约束的体积和逻辑复杂度，也能减轻后续求解负担、提高约束求解的效率，还能为约束求解结果的缓存和重用操作节省空间和时间.

2.1.1非相关约束分支切片

非相关约束分支切片又称为切片(slicing)或约束独立(constraints independent)，是通过把路径约束条件切分成一个或多个不相交的约束子集再求解的技术. 同一程序或不同程序中，很少情况下会存在两条相同的路径，如果对整条路径约束及结果进行缓存，则其重用性会非常低. 另一方面，程序中因为分支条件而使得路径数量的逐渐增多，会存在大量的相似路径. 例如，对路径约束中某一条件约束取反从而生成另一条路径约束，除了取反的这一约束条件以外，其余约束都是相同的. 切片算法的提出能使得大部分相似路径约束求解结果的重用变得可能而且实用.

一条路径约束可以映射到无向加权图中，称这一类图为约束图(constraints graph). 在约束图G=(V,E)中，节点V表示约束式，而节点之间的边E则表示两条约束之间的共享变量. 例如，在图2中路径约束为

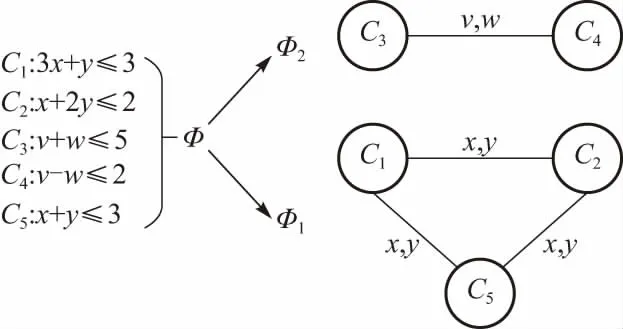
图2 非相关约束分支切片示例Fig.2 Explanatory chart of non-correlation restriction sliding

{3x+y≤3,x+2y≤2,v+w≤5,

v-w≤2,x+y≤3}，

因为约束式C1、C2、C5和C3、C4没有共享变量，所以路径约束Φ可被切分成两个约束子集

Φ1={C1,C2,C5}=

{3x+y≤3,x+2y≤2,x+y≤3}，

Φ2={C3,C4}={v+w≤5,v-w≤2}.

约束子集对应的两个约束子图如图2所示.

切片对约束求解的好处有两方面，一是能够简化路径约束，将路径约束碎片化能减小求解约束集的体积，加快求解速度. 事实上，在求解器内部也会对约束集做切片工作，但会消耗比较大的计算量. 外部切片再求解能减小求解器求解负担，提高求解效率. 二是有助于求解结果的重用. 符号执行中存在大量的相似路径，对路径约束进行切片，能增加相似路径求解结果重用的概率.

切片策略由Cristian Cadar等提出[18,42]，并在其开发的EXE和KLEE工具中配合约束结果缓存策略同时使用. 后来Mayhem[20]、Green[45]、GeenTrie[46]、Memoise[43-44]以及Recal[47]等工具中都有采用此方法进行约束求解优化. 切片策略能独立应用于约束求解的优化，同时又是其他策略如存储、搜索等步骤的基础，配合约束结果缓存能取得更好的性能优化效果.

2.1.2约束简化

约束简化在英文文献中又称为“Simplifying”或“On-the-fly Expression Simplification”. 现有的符号执行工具提出了很多针对单条约束条件的简化技术，能够精简约束式，减轻求解负担.

① 表达式重写(expression rewriting). 表达式重写包括一系列对单条约束式的简化技术，这些简化技术类似于编译器中对编译程序中表达式的简化措施，具体如表2所示.

表2 表达式重写措施及示例Tab.2 Illustrative measures of expression rewriting

② 约束集简化(constraint set simplification). 在符号执行中，随着路径约束中约束式的增加，对其中符号变量的约束限定范围也可能会更加严格. 这已特性使得对其进行先行化简变得可行和必要. 例如，当前路径约束为x>5，随着符号执行的进行，有新的约束为x=6加入到此路径约束中时，因为x=6对x的取值范围限定更加严格，所以之前的约束x>5将被直接简化为true，即直接将其从路径约束中删除. 约束集简化在KLEE中提出，并取得了良好的优化效果. 同时CUTE中也提出了称为common sub-constraints elimination的简化措施，方法是类似的，其实验结果证明此方法能减少64%～90%的约束式的体积[41].

③ 隐含值的实际化(implied value concretization). 隐含值实际化主要是把路径约束中隐含实际值的符号变量全部以实际值替换，以此达到简化路径约束的目的. 例如路径约束中有约束式x+5=6，则经过计算可以得到x是一个隐含值，可以对其进行简化处理，得到x=1. 而后续出现x变量的约束式中，对x的值都可以用实际值替换，如x+y<8∧x+z>12，最终将被化简为y<7∧z>11. 隐含值实际化技术在KLEE中被提出.

④ 最大公约数化简. Recal[47]中也采用了一些技术对约束式进行简化，如除以所有变量系数和常量的最大公约数等(例如2x+2<4可被简化为x+1<2).

⑤ 数组约束编码简化. 数组在符号路径约束中普遍存在，约束数组求解问题是符号执行中求解开销最大的问题之一. 许多程序的输入都包含各种形式的数组(如字符串通常是以字符数组的形式被编码)，开发人员也普遍采用数组完成各种数据结构(如哈希表和向量等). 另外，底层代码的指针操作常常使用数组模型[48]. 虽然使用实际索引的数组能被相似的方式处理，但因为指向位置的不确定性使得符号索引更难管理.

Perry等[49]提出了一系列不丢失语义的数组操作编码转换方法，通过对符号执行期间的上下文信息的分析，把数组操作转换成语义上等价的且满足判定条件数组约束的形式. 此种转换方法能使用更简单的编码方式表示数组的操作，并能够大规模改进带有数组操作的符号执行的性能.

2.1.3冗余约束精简

在符号执行中，路径约束可以看成是由m条约束条件，n个变量组成的约束集

Ax≤b.

(1)

如果删除某些约束式后，约束集的可行域及求解结果不变，则被删除的一条或多条约束式是冗余的.

图3形象地说明了路径约束中的冗余约束问题. 假设灰色区域S={x∈Zm|Aix≤bi}是路径约束的可行域(feasible region)，而Sk={x∈Zm|Aix≤bi,i≠k}是删除第k条约束之后的可行域，当且仅当S=Sk时，称第k条约束条件是冗余的.

冗余约束精简(redundant constraints elimination)是指在调用SMT求解器进行求解之前对逻辑上冗余的约束式进行删除的操作. 冗余精简能够加快约束求解的速度，同时也能节省内存空间，也为后续的匹配查找、求解结果重用节省时间.

Green[45]中的切片和约束式标准转化工作使得变量顺序相同，但变量命名和逻辑表达形式不一样的约束式转化为唯一的标准表达形式，这也能一定程度上精简约束式.

Recal[47]中提出Normalization中的算术转化措施通过对相同变量合并、逻辑转化以及除以变量和常数的最大公约数的方式能够进一步精简约束式. 此外，其中的“redundant clauses elimination”作为其Normalization部分工作组的最后一步，能通过简单的算术对比将系数相同但常数不一样的约束式进行精简. 如x+y<3和x+y<2，这两个约束式中x+y<3会被判定为冗余约束.

2.2 求解时优化

求解时优化主要是在调用约束求解器求解的过程中涉及到的一些优化措施. 具体包括域约简优化、快速不满足性检查、消除不相关约束、使用断言栈优化求解、多求解器支持等.

2.2.1域约简优化

域约简优化(domain reduce optimization)是由Erete 和Orso等提出[50]，主要是在符号执行中使用域与上下文信息对约束求解的性能进行优化. 实验结果表明，限定路径约束的输入域可能帮助求解器更快地找到解. 具体思路是在求解时把路径约束的全部符号值用实际值替换，只留一个符号变量让求解器求解，如果无解，则把另一个符号变量符号化再求解，依次类推不断增加符号变量，直到有解为止. 在上述过程中，每次增加符号变量的过程就是不断扩大变量作用域(输入域)的过程. 在路径约束有解的情况下，输入的大小关系着求解器对路径约束的求解难度和求解开销，输入域越小，求解速度越快，开销越小，但如果解不存在，则需要再次增大输入域；反之，输入域越大，求解速度越慢，开销越大，但同时求出可行解的概率越大. 所以域约简优化技术主要是对输入域和求解难度、求解速度之间取最佳权衡和折衷.

2.2.2快速不满足性检查

快速不满足性检查(fast unsatisifiability check)技术同样在CUTE[41]提中出. 此技术主要对由取反而生成的新路径约束进行快速的逻辑语法上的判断，如果路径约束中存在逻辑上相互冲突的约束式，则马上返回为unsat，不需要再交给约束求解器对其进行求解. 例如有路径约束为(x>5)∧(y<10)∧(x≥6)，对其最后一条约束取反之后生成的新的路径约束为(x>5)∧(y<10)∧(x<5). 在对其做快速不满足性检查发现约束式(x>5)和约束式(x<5)在逻辑语法上有冲突，则无需在调用约束求解器对其做可达性求解，直接返回unsat的结果. CUTE论文中的实验证明，快速不满足性检查能够减少对求解器60%～90%的调用检查，对约束求解性能起到了很大的优化作用.

2.2.3不相关约束删除

不相关约束删除(irrelevant constraint elimination)首先在KLEE中提出，在符号执行中，不断地对路径约束条件取反会生成大量的相似路径约束，为了判定这些路径的可行性及生成测试用例，需要频繁调用求解器进行求解. 而与取反前的路径相比，新路径可达性只与被取反的分支条件的符号变量相关，所以一种有效的优化约束求解的方法是删除与当前分支条件变量无关的约束后再进行求解.

Domestic cosmetic brands concern about korean brands 12 1

不相关约束删除是切片策略的特殊应用，根据被取反分支条件的相关性，通过把新的路径约束切分成相互独立的两个约束子集. 然后只对与取反分支条件变量相关的约束子集求解，其余的约束子集则重用之前的求解结果. 通过这种方式能减小约束体积，减轻逻辑复杂度.

例如，假设当前执行的路径条件为(x+y>10)∧(z>0)∧(y<12)∧(z-x=0)，如果需要对条件(y<12)取反，即对(x+y>10)∧(z>0)∧┐(y<12)约束求解产生新的路径，因为变量y只与x有关，所以可以直接把与Z相关的约束删除，直接求与x和y相关的约束. 在求解完成生成新的x和y的值之后，在加上取反之前的z值，则为新的走不同路径的输入. 此思路还需要解决指针解引用、数组索引等问题，在相关文献[41-42,51]中有详细阐述.

2.2.4使用断言栈优化求解

求解器内部断言栈(assertion stack)是由求解器本身维护，通过求解器提供的命令(如push和pop命令)合理使用断言栈能够共享不同约束集之间相同变量的定义、声明以及约束条件等，这样不但能减少求解器内部重复的计算开销，还能同时减小存储空间重复申请和释放带来的开销，提高求解器求解效率. 使用栈的优势是对于一些相似问题，不用每次重复定义变量求解，而且对于相似约束，可以共用变量. 这样能节省空间和时间. Liu等[52]首次验证了基于断言栈比缓存技术更能提升求解器的求解效率.

2.2.5多求解器支持

在表1中可以看到，大部分符号执行工具只使用了单个求解器求解，如Bitblaze使用了STP，而SAGE使用了Z3求解器. 这导致在实验中对单一符号执行工具和约束求解器的实验得出的结论并不具有通用性. 其次，不同求解器的求解性能、擅长求解的理论并不一样，增加对多求解器的支持(multi-solver)，根据路径约束的类型和特征选择不同的SMT求解器，能够增强约束求解的性能，这一结论已经在Palikareva H等的论文[53]中得到证实.

2.3 求解后优化

求解后优化指在调用约束求解器求解之后对约束求解结果缓存和重用. 本文大致将这些工作分为增量求解以及其他的缓存和重用策略.

2.3.1增量求解

在符号执行中，相邻路径约束有很多公共的约束条件，可以利用以前相似路径约束的求解结果，然后对已求解约束的子集和超集进行预判或者验证，这样能减少对求解器调用的次数，或者减小求解的开销. 这一策略被称为增量求解(incremental solving)，已经在KLEE和CUTE等一些工具中被使用.

在KLEE中这一策略又称为反例缓存(counter-example caching)调度算法，KLEE把所有约束及其对应的求解结果做缓存处理以便重复使用. 例如缓存中存有如下的约束集及其求解结果(x>6)∧(x+y<12):{x=7,y=4}，当有相似的约束集需要求解的时候，KLEE会首先在缓存中查找有无可以重用的结果：如果是某个约束集的子集(如(x+y<12))，则直接返回缓存中的结果，因为超集对变量求解的域的结果比子集有更强的约束，所以其结果同样适用于子集；如果是某个缓存中约束集的超集，如(x>6)∧(x+y<12)∧(y>=2)，则先试探缓存中子集的求解结果是否能满足超集中的约束条件，如果不满足则再调用求解器求解. 事实上在符号执行过程中，新增加的约束往往不会使得之前的约束求解结果无效. 而检查某些值在约束集中是否适用相对于对整个约束集求解而言只会耗费非常小的计算量. 这也是这一策略能实际应用到符号执行中并能改善其性能的原因.

2.3.2缓存和重用

除了上面提到的增量求解外，研究人员还提出一些适用范围更广的缓存和重用策略，增量求解只适用于已知求解的约束的子集和超集，而后续提出的这些缓存策略则包含了更多利用缓存区优化约束求解的方法.

Yang等[43-44]提出使用Trie树来存储程序的执行状态和结果. 使用Trie树的好处在于对于相同前缀的约束条件选择不需要重复存储，这样能节省存储内存空间又能加快检索匹配速度. 在Memoise中，Trie树中每个节点并没有存储路径约束条件，而是只记录三样数据约束节点的选择(choices)，所在的方法(method)及其在方法中的指令偏移(instruction offset).

Green[45]中，路径约束经过切片、规范化(canonization)等步骤之后与求解结果一起存入了键值对存储的数据库Redis中，使用Redis的好处是能根据配置的阈值将结果存在内存中，这加快了存储和查询的速度. Green提出的对约束式规范化转换的思想使得不同变量名但顺序和逻辑都相同的约束式具有了唯一的表达式，这让Green对约束求解结果的重用范围不能仅仅局限于程序内部，还扩展到了不同程序中.

GreenTrie[46]从逻辑上扩展了KLEE和Green对求解结果的重用匹配策略，对求解结果的逻辑子集和超集进行判断和匹配. 此外GreenTrie还把Green中的存储载体从Redis换成了Trie树.

Recal[47]使用了一种新的方式来标准化处理切片后的约束式，使得变量顺序不同但逻辑上相同的约束式具有唯一的表达形式，这增加了求解结果重用的概率.

约束求解结果缓存和重用能独立应用于约束求解性能优化，又能与其他优化策略配合使用取得更好的效果. 在KLEE中，切片和缓存策略独立应用于约束求解性能优化时，各自对性能的提升比较有限；但当两者同时应用到KLEE中的时候，KLEE对约束求解的性能有了数量级上的提升，特别是当程序比较大的时候，这两者相结合所显现出的优势就更加明显.

3 未来研究展望

虽然本文提到的研究工作都在约束求解方面取得了较大的研究进展，但当前各项研究都还存有一定的局限性，而符号执行应用于大型程序的研究过程是一个多种性能优化措施并行且不断地对性能调优的过程，约束求解问题的研究仍然还有待继续. 未来的研究工作可以在以下几个方面进行.

① 提高路径约束逻辑精简率. 在符号执行中，对路径约束中的冗余约束进行精简既能减小路径约束的体积和逻辑复杂度，又能减轻求解器负担、提高约束求解的效率，还能为后续的约束求解结果的缓存和重用操作节省空间和时间. 当前KLEE、Green、GreenTrie和Recal等符号执行工具都有提出对约束简化和简单的约束式删减工作，但这些工具要么是对单条约束式独立的算术式化简，要么是对相似约束式的对比进行可行域的缩减，都不能真正从逻辑上根据路径约束的可行域进行冗余约束判定和精简.

② 提高约束求解结果存储和重用的效率. 现有的研究工作在约束求解结果和重用方面取得了比较大的进展，并证明历史查询求解的结果能够被同一程序甚至是不同程序重复使用，很大程度上减小了对SMT求解器的调用. 但这些工作得益于以空间换时间的代价，设计更加高效的存储、查询匹配策略将对约束求解的性能带来更大的提升.

③ 约束求解并行化. 当对大量程序进行符号执行测试的时候，基于单台服务器的测试将需要非常长的CUP处理时间. 约束求解并行化处理能够加快对测试用例的生成，提高符号执行的效率. 在Bucur S等的工作[54]以及Vertitesting[25]中已经使用了分布式架构用于约束求解的并行化处理，并取得了显著的性能提升.

④ 约束求解配置预测. 路径约束条件的编码形式严重影响着求解器的求解性能. 对于不同的SMT求解器，因为对其支持的理论的不同配置，总的求解时间变化范围可达两个数量级[55]. 某种求解配置只对某些约束子集具有最佳的表现，而对于其他约束子集则未必，所以如果能够在求解之前对待求解的约束集进行预判，然后根据判定结果选择合适的配置，可以使得对此次的求解具有最佳的性能开销. 而求解的配置可能是多种求解策略配置并行组合的配置，这些配置还容易加大对CPU计算资源的消耗. 所以一种可行的方法是，使用机器学习的算法根据待查询语句的特点预测出最佳的求解器配置. 这些配置特征可以是查询的AST大小、嵌套的数组操作数量、ITE节点的数量等. 或者借助深度学习算法应用到配置策略选择上，借助其自动特征提取和分类的能力，使得配置决策更加智能化.

4 结束语

作为符号执行的瓶颈问题之一，约束求解问题的研究对改善符号执行的可扩展性起到了至关重要的推动作用. 本文对近年来的约束求解问题的研究按照调用SMT求解器的不同阶段进行了梳理分类，并对每个阶段的相关工作进行了详细的介绍. 随着约束求解问题以及可满足模理论本身研究进展的增多，符号执行中的约束求解问题将会得到更大的缓解.