顶张式立管液压气动式张紧器的数值模拟

陈柏全，余 杨，余建星，徐立新，吴 晨，康煜媛

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.上海交通大学 高新船舶与深海开发装备协同创新中心，上海 200240；3.中国石油管道局工程有限公司 天津分公司，天津 300457)

海上油气开发面临众多挑战，其中之一就是设计出经济安全的立管系统[1]。顶张式立管是海上油气开发系统的重要组成部分，连接着海底井口设备和水上浮式平台，进行油气输送。浮式平台与顶张式立管之间通过张紧器进行连接，张紧器对于确保顶张式立管的正常运行具有关键性作用。一方面，张紧器为顶张式立管提供足够的顶部张力，确保立管不会因张力不足而发生屈曲。另一方面，当浮式平台发生升沉运动时，张紧器通过调节平台和立管之间的相对运动，避免立管顶部因张力过大而发生损坏。

国内外学者对顶张式立管开展研究，包括受迫振动[2-4]、涡激振动[5-7]和参数振动等。在顶张式立管的模拟分析过程中，采用了不同的方法模拟张紧器。其中，最常用的方法是恒定集中力法，该方法通过在立管顶部施加竖直向上的恒定张力来模拟张紧器的作用。例如，Chang等和Zhang等采用ABAQUS对顶张式立管进行模拟分析，他们的模型均采用恒定集中力模拟张紧器。Mao等的理论分析和物理实验模型同样采用恒定集中力模拟张紧器。恒定集中力模型不能反映平台升沉运动引起的张紧器张力变化，于是有学者采用刚度恒定的线性弹簧模拟张紧器。例如，Kuiper等[8]在立管分析模型中采用线性弹簧模拟张紧器，并给出了弹簧刚度的经验表达式。杨和振等[9-10]也采用线性弹簧模拟张紧器，研究立管的参激振动问题。唐友刚等[11]在立管的稳定性实验中同样采用线性弹簧模拟张紧器。然而，在实际使用中张紧器的刚度并不是保持不变的，会随着冲程的变化而变化，体现出非线性的特点，于是有学者采用简单的非线性弹簧模拟张紧器。Yu等[12]建立了简单的气缸活塞模型，并推导得到非线性弹簧模型的表达式。Yang等[13-14]采用了相同的非线性弹簧模型，并比较了线性弹簧模型和非线性弹簧模型之间的差别，强调了采用非线性弹簧模型的重要性。

国内外学者在进行立管分析时采用了较简单的张紧器模型，而且没有合理地处理平台-张紧器-立管之间的耦合运动关系，与实际工程情况有一定差距，因此需要进一步研究更加符合工程实际的张紧器模拟方法。本文以常规液压气动式张紧器为研究对象，通过考虑平台-张紧器-立管之间的耦合运动关系以及张紧器的非线性特性，建立较为合理的张紧器模型。考虑立管的真实截面布置以及采油树的作用，建立能够应用于工程实际的顶张式立管三维有限元分析模型。最后，对不同的张紧器模拟方法进行对比研究。

1 张紧器的模拟

1.1 张紧器的主要结构

本文以常规液压气动式张紧器为研究对象(见图1)，其主要结构包括：①盒式框架，连接液压气柱的顶端与浮式平台的生产甲板，浮式平台的运动通过盒式框架传递到张紧器上；②导向滚轮，固定在盒式框架上，能够约束立管的水平运动，对立管起到扶正作用；③液压气柱，与立管之间存在一定夹角，通过活塞的伸缩运动，调节顶张式立管受到的张力；④张力环，液压气柱的底端与顶张式立管的连接位置，张紧器的张力通过张力环施加到立管上。

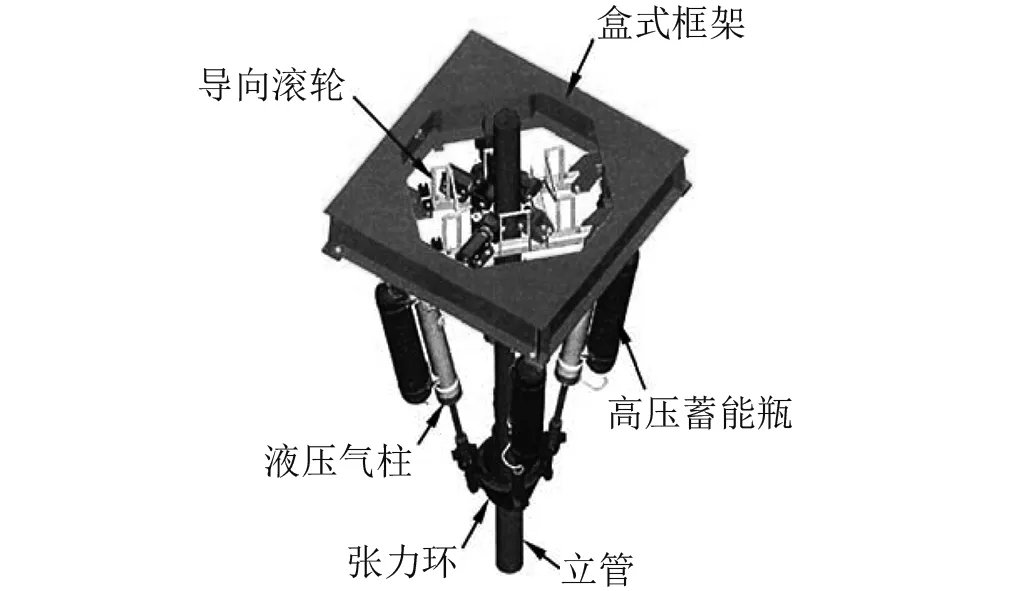
图1 常规液压气动式张紧器[15]Fig.1 Conventional hydro-pneumatic tensioner

张紧器的核心部件是液压气柱的液压气动系统(见图2)，其主要由四部分组成：①低压氮气瓶；②液压缸(包括活塞和活塞杆)；③高压蓄能瓶；④连通液压缸和高压蓄能瓶的油管。这四部分形成了一个通过液压油传递压力，用惰性气体作为弹性介质的密闭弹性系统。

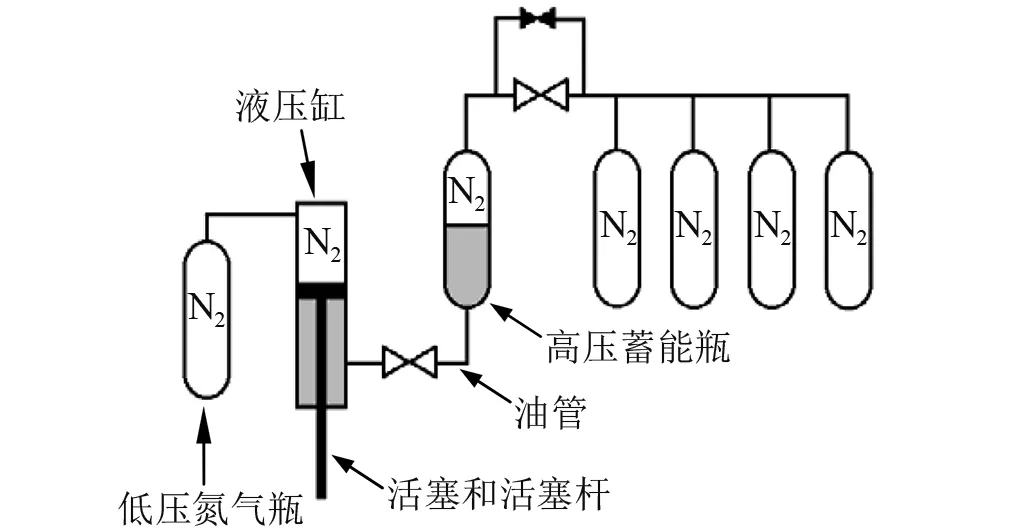
图2 液压气柱的液压-气动系统Fig.2 Hydro-pneumatic system of the cylinder

针对常规液压气动式张紧器，合理的模拟方法包括两个关键条件：①合理模拟液压气柱的张力特性；②合理处理平台、张紧器和立管之间的运动耦合关系，将浮式平台的运动准确地传递和施加到立管上。

1.2 液压气柱张力特性的模拟

对单个液压气柱进行研究，液压气柱活塞和活塞杆的受力示意图，如图3所示，忽略活塞和活塞杆的加速度，则活塞杆受到的张力由式(1)计算

T=Pr(Ap-Ar)-PlAp-Mg+Ff

(1)

式中：T为活塞杆受到的张力，沿液压气柱的方向；Pr为液压缸下油腔的瞬时压强；Ap为活塞面积；Ar为活塞杆面积；Pl为低压氮气的气体压强；M为活塞和活塞杆的质量；Ff为活塞与液压缸之间的摩擦力。

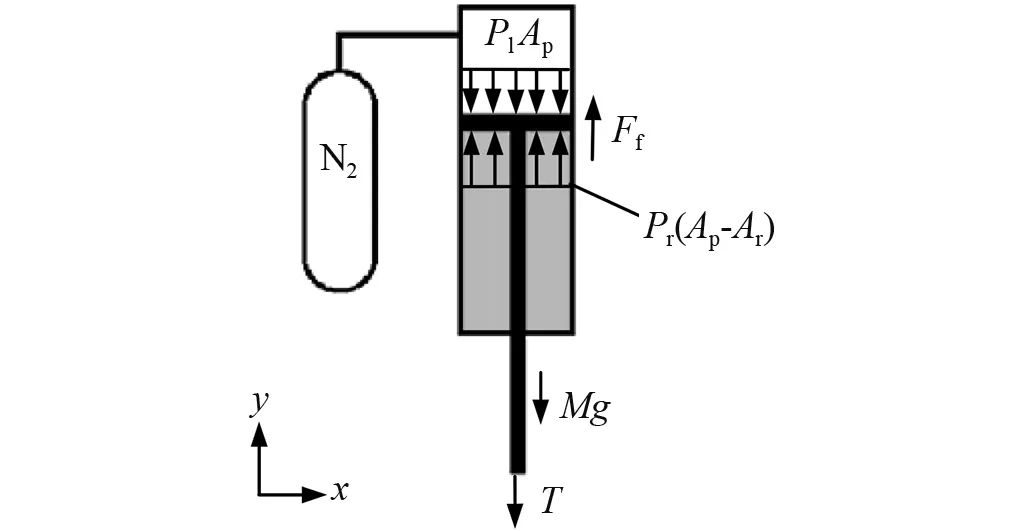
图3 液压缸的受力示意图Fig.3 Schematic of hydro-pneumatic cylinder

假设张紧器中的工作气体在状态变化时不与外界发生热交换，即工作气体符合绝热状态变化规律，则高压蓄能瓶和低压氮气瓶内气体的方程为

(2)

(3)

式中：k为气体常数，根据不同气体的性质一般可取1.0～1.3；Ph，Vh分别为任意状态下高压气体的压强和体积；Ph0，Vh0分别为初始平衡状态下高压气体的压强和体积；Pl，Vl分别为任意状态下低压氮气的压强和体积；Pl0，Vl0分别为初始平衡状态下低压氮气的压强和体积。

忽略液压油的可压缩性，则任意时刻高压气体体积Vh和低压氮气体积Vl计算如下所示

Vh=Vh0+(Ap-Ar)sp

(4)

Vl=Vl0-Apsp

(5)

式中：sp为活塞冲程，当sp>0时为正冲程，时sp<0为负冲程。

将式(4)、式(5)分别代入式(2)、式(3)，则可分别得到在任意时刻高压气体和低压气体的气体压强的计算公式

(6)

(7)

忽略液压油经过油管时的压强损失，则有

Pr=Ph

(8)

液压缸的缸筒与活塞之间存在相对运动，它们之间的摩擦力对张紧力有很大影响。本文采用一个简化模型计算张紧器的摩擦力[16]

(9)

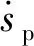
将式(6)～式(9)代入式(1)，得到液压气柱的张力计算公式如下

(10)

令Th0=Ph0(Ap-Ar),Lh0=Vh0/(Ap-Ar),Tl0=Pl0Ap,Ll0=Vl0/Ap,则式(10)化成

(11)

由式(11)可以看出，单根液压气柱的张力T和活塞冲程sp的关系是非线性的。

在传统的张紧器模拟分析中，常将张紧器简化为线性弹簧。将式(11)进一步线性化，得到计算单根液压气柱张力的线性弹簧模型

(12)

在目前的工程应用和研究中，通常忽略低压氮气和活塞重力的作用，此时式(11)简化成

(13)

式(13)与Yu等推导得到的公式相同，是目前工程中最常用的公式。

还有部分学者采用竖直向上的恒定集中力，即张紧器的初始张力模拟张紧器，如式(14)所示

Tnormal=NT0cosθ

(14)

式中：N为张紧器液压气柱的数量；θ为液压气柱与立管之间的夹角。

1.3 浮式平台、张紧器和立管之间关系的处理

现有的文献通常忽视浮式平台、张紧器和立管之间运动关系的处理，将平台运动直接施加到张紧器的顶端或者立管上，这显然与实际工程不符。实际上，平台运动应施加在平台重心，然后通过张紧器、导向滚轮等结构传递给立管。因此，本文考虑平台-张紧器-立管的运动耦合关系建立两种分析模型，即恒定集中力模型(见图4(a))和弹簧-阻尼模型(见图4(b))。针对恒定集中力模型(见图4(a))，在平台重心和导向滚轮之间建立水平方向的耦合约束以约束立管水平方向的运动，平台的运动将通过平台重心-导向滚轮传递给立管。针对弹簧-阻尼模型(见图4(b))作如下处理：①在平台重心和导向滚轮之间建立水平方向的耦合约束以约束立管水平方向的运动；②在平台重心和生产甲板之间建立刚体连接模拟平台刚体内部的运动关系；③在盒式框架和张力环之间建立弹簧-阻尼单元模拟液压气柱。这样平台的运动一方面通过平台重心-导向滚轮传递给立管；另一方面通过平台重心-生产甲板-液压气柱-张力环传递给立管。通过以上处理，能够有效考虑平台-张紧器-立管之间的运动耦合关系。

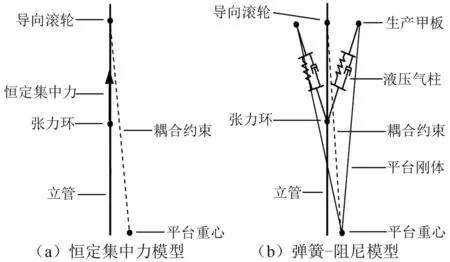
图4 浮式平台、张紧器和立管之间关系示意图Fig.4 Schematic of hydro-pneumatic cylinder

2 顶张式立管的有限元模型

本文采用有限元分析软件ABAQUS建立顶张式立管有限元分析模型。

如图5所示，顶张式立管主要由外套管(单层或多层)和内部油管组成，在有限元分析过程中需要对立管截面进行等效。等效截面的拉伸刚度、弯曲刚度以及扭转刚度由以下公式计算获得[17]

EAeq=EAcasings

(15)

EIeq=EIcasings+EItubing+EIotherlines

(16)

GJeq=GJcasings+GJtubing+GJotherlines

(17)

式中：E为弹性模量；G为剪切模量；Aeq，Ieq，Jeq分别为等效后的截面面积、惯性矩和极惯性矩；Acasings，Icasings，Jcasings分别为外套管的截面面积、惯性矩和极惯性矩；Itubing，Jtubing分别为内部油管的惯性矩和极惯性矩；Iotherlines，Jotherlines分别为其他辅助管线的惯性矩和极惯性矩。

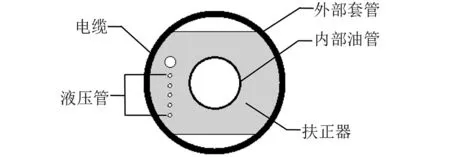
图5 立管截面Fig.5 Cross section of top tensioned riser

张紧器和浮式平台采用第1节介绍的方法进行模拟。采油树是位于立管顶部的质量块，其质量达到立管质量的15%以上。而目前关于顶张式立管动力响应的研究，通常忽略采油树的作用，这显然与工程实际不符。因此，本文在建立立管分析模型时考虑采油树的作用，并采用点质量进行模拟。立管与海底井口之间采用应力接头连接，因此设置为固定边界条件。立管上部受到平台运动的作用，设置为运动边界条件，平台运动施加在平台重心位置。以弹簧-阻尼模型为例，所建立模型如图6所示。

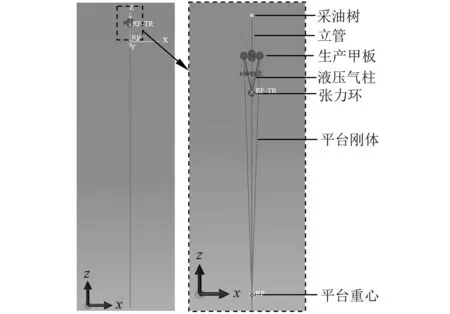
图6 有限元模型图Fig.6 Finite element analysis model

立管的响应计算分为两个分析步：第一步为静态分析步，施加立管受到的重力、浮力和海流力，针对恒定集中力模型还需在张力环处施加初始张力；第二步为动态分析步，在平台的重心位置施加平台运动。立管受到的浮力、拖曳力和惯性力通过Abaqus/Aqua模块施加。在施加平台运动时，本文建立的模型能够施加平台的平动和转动的多自由度运动。

3 算例分析

第1节中介绍了4种张紧器模拟方法，即非线性的弹簧-阻尼模型(见式(11))、线性的弹簧-阻尼模型(见式(12))、传统的简化模型(见式(13))以及恒定集中力模型(见式(14))，本节对不同张紧器的模拟方法进行对比分析。

3.1 模型参数

本文采用一根应用于中国南海的顶张式生产立管开展研究，该立管由单层外套管和内部油管组成，截面属性如表1所示。张紧器包含4个液压气柱，液压气柱与立管之间的初始夹角为12°。单个液压气柱的结构参数如表2所示。采油树的质量为8 554.63 kg。另外，在计算过程中本文气体常数k取1.3，等效摩擦力因数Cf取0.04。

经过计算，不同张紧器模型的竖向张力与活塞冲程的关系曲线，如图7所示。由图7可以看出，由简化模型计算得到的张力始终比由线性和非线性模型计算得到的大，而且在正冲程区域的差异比在负冲程区域的大。由此可见，由于忽略了低压氮气和活塞重力的作用，传统的简化模型过高评估了张紧器的张力水平。此外，由线性模型和非线性模型计算得到的张力在活塞冲程较小时差别较小，但随着活塞冲程的增大，二者之间的差异也随之增大。

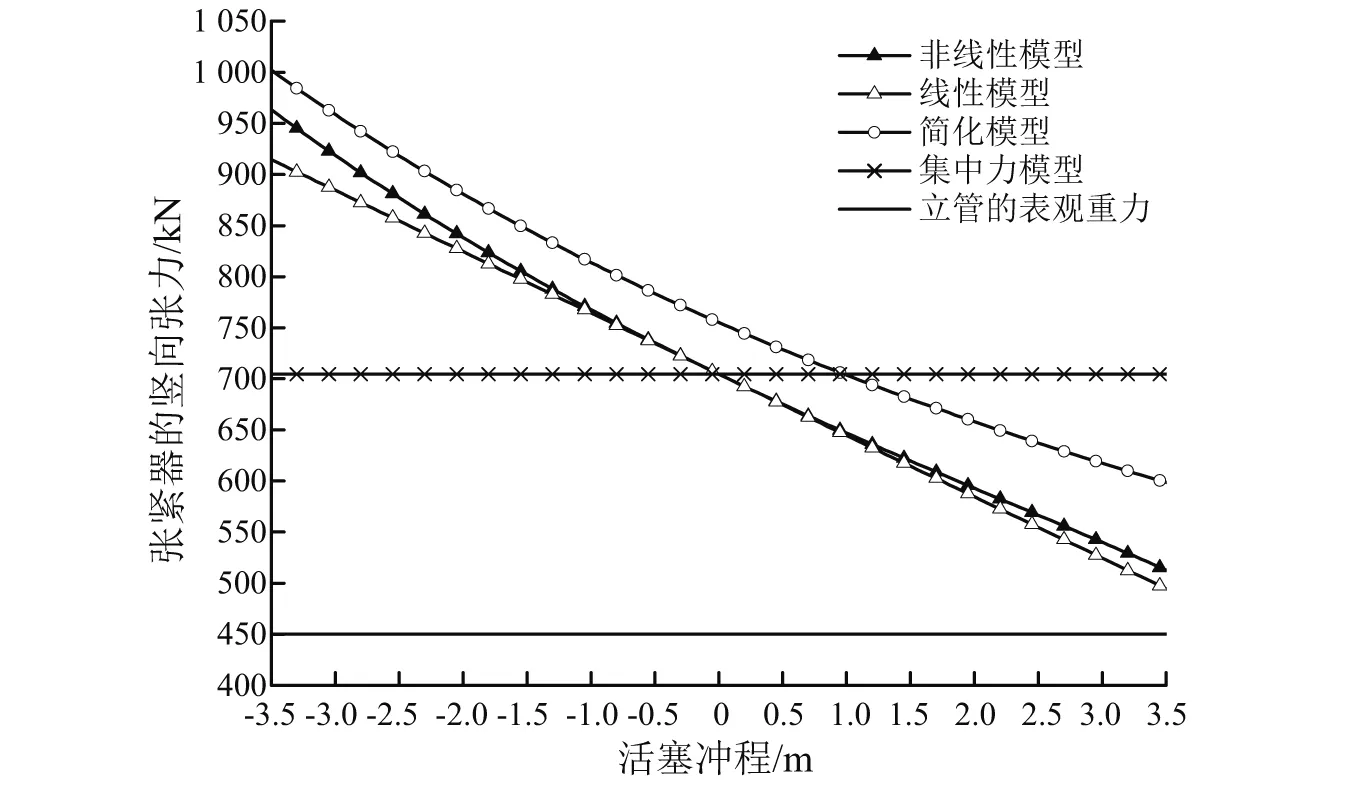
图7 张紧器的竖向张力与活塞冲程的关系曲线Fig.7 Tensioner vertical tension and stroke relation

为了更加充分地进行对比研究，本文基于各张紧器模型的竖向张力的大小变化，选取3种典型工况进行研究。在施加平台运动时，考虑了升沉运动和水平运动的耦合作用，如表3所示。另外考虑沿水深线性变化的恒定流作用，海面流速大小分别为1 m/s，1.5 m/s，2 m/s，海底流速均为0，海水密度为1 025 kg/m3，拖曳力系数为1.0，惯性力系数为2.0。本文忽略涡激振动的作用。

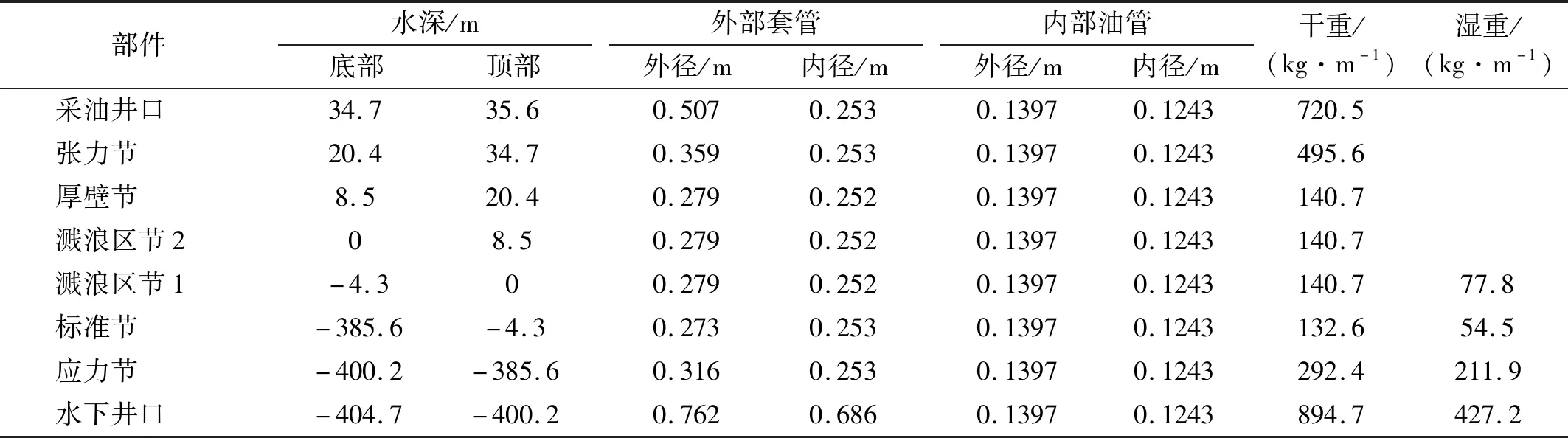
表1 顶账式立管的截面属性Tab.1 Sectional properties of the top tensioned riser

表2 液压气柱的参数Tab.2 Parameters of the hydro-pneumatic cylinder

表3 平台运动Tab.3 Platform motion

3.2 结果对比分析

3.2.1 立管的最大张力分布

图8为不同工况下沿立管的最大张力分布。由图8可以看出，在不同的工况下，恒定集中力模型的最大张力分布几乎保持不变，其不能反映立管张力大小的周期变化。随着工况条件的越来越剧烈，弹簧-阻尼模型与恒定集中力模型之间的区别也越来越大。在张力环以下的立管部分，简化模型的最大张力始终比其他模型的大，说明了采用简化模型会过高评估立管受到的张力。在3种不同工况下简化模型的最大张力比非线性模型的约分别大48.46 kN (7.50%)，43.57 kN (6.01%)以及 41.18 kN (5.11%)。对比线性和非线性模型，在工况条件不剧烈时(工况一)，二者之间几乎没有差别，但随着工况条件越来越剧烈(工况二和工况三)，二者之间的差别也越来越明显。在工况三条件下，非线性模型的最大张力比线性模型约大28.22 kN(约4.0%)。

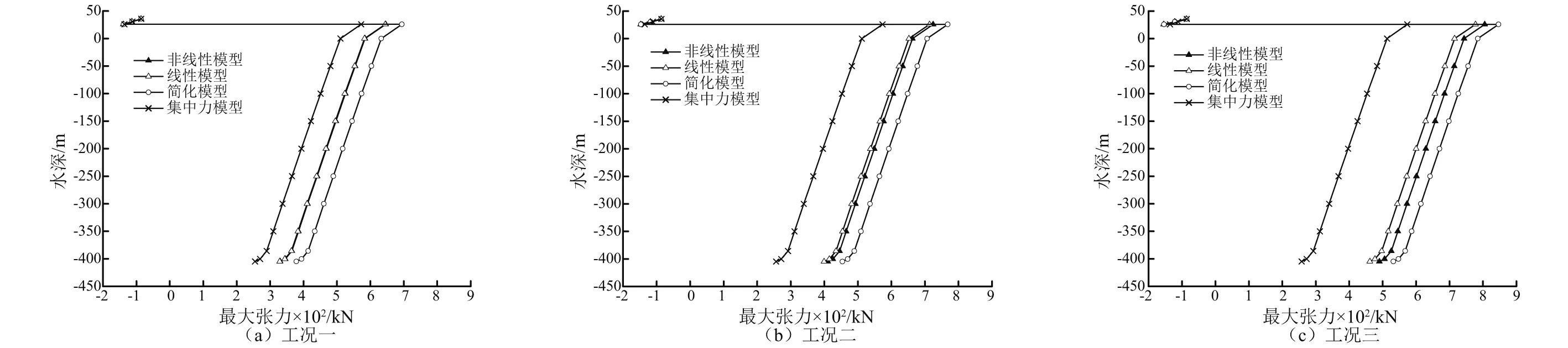
图8 立管最大张力分布Fig.8 Maximum tension distribution along riser

3.2.2 立管的最大弯矩分布

图9为不同工况下沿立管的最大弯矩分布。由图9可以看出，在立管底部恒定集中力模型和简化模型的弯矩比线性和非线性弹簧-阻尼模型的小。在3种不同工况下，简化模型比非线性模型约分别小4.13 kN·m(2.44%)，13.90 kN·m (5.02%)和23.15 kN·m (7.10%)，而集中力模型比非线性模型约分别小22.91 kN·m (13.54%)，42.23 kN·m (15.25%)和24.80 kN·m (7.61%)。值得注意的是，在张力环位置恒定集中力模型出现了过大的弯矩，这是由于恒定集中力模型的对立管仅有竖直向上的力，而没有水平力的约束。此外，在不同工况条件下，线性和非线性弹簧-阻尼模型得到的弯矩分布结果基本一致，这是由于在本算例下，线性和非线性模型之间的张力差别，不足以引起立管弯矩的差别。可见，浮式平台、张紧器和立管之间关系的处理以及张紧器的张力大小对立管的弯矩具有重要影响，其影响主要体现在立管底部和张力环位置。

图9 立管最大弯矩分布Fig.9 Maximum bending moment distribution along riser

3.2.3 立管的最大水平位移分布

图10为不同工况下沿立管的最大水平位移分布。由图10可以看出，简化模型的最大水平位移均小于其他模型，这是由于简化模型计算得到的张紧器张力要大于其他模型。在3种不同工况下简化模型的最大水平位移比非线性模型约分别小0.10 m (3.14%)，0.33 m (5.28%)和0.32 m (4.27%)。当环境条件较为剧烈(工况二和工况三)，在平均水面至水下150 m之间的立管部分，恒定集中力模型的水平位移比弹簧-阻尼模型大，这是由于恒定集中力模型对立管仅有竖直向上的力，而没有水平力的约束。在3种不同工况下恒定集中力模型的最大水平位移比非线性模型分别大0.02 m (0.58%)，0.31 m (5.00%)和0.44 m (5.86%)。另外随着环境条件变剧烈，线性弹簧-阻尼模型的水平位移比非线性弹簧-阻尼模型的略大，这是由于线性弹簧-阻尼模型的张紧器张力相对较小，但二者之间的差别不十分明显。由此可见，张紧器的张力大小对立管的水平运动具有影响，而且主要体现在立管上部位置。

图10 立管最大水平位移分布Fig.10 Maximum lateral displacement distribution along riser

3.2.4 立管中点的垂向位移

由于立管的垂向位移可能向上或者向下，为了体现不同张紧器模型下立管的垂下位移特性，本文选取立管中点的垂向位移时间历程作为对比参数，如图11所示。由图11可以看出，由于恒定集中力模型的张紧器张力不随工况条件发生变化，立管中点的垂向位移的运动范围比弹簧-阻尼模型的小。由于简化模型的张紧器张力比线性和非线性模型的大，简化模型的垂向位移相对于线性和非线性模型的垂向位移相对向上偏移。另外，由于线性弹簧-阻尼模型提供的张紧器张力相对于非线性弹簧-阻尼模型偏小，线性弹簧-阻尼模型的垂向位移相对于非线性弹簧-阻尼模型的垂向位移在向下偏移，并且随着工况条件越来越剧烈，二者之间的差别也越大。

图11 立管中点垂向位移的时间历程Fig.11 Vertical displacement time history of riser center

4 结 论

本文综合考虑张紧器的刚度特性以及平台-张紧器-立管之间运动耦合关系的处理，研究不同张紧器模型的合理性和适用性，得到以下结论：

(1)由于恒定集中力模型的张紧器张力始终保持竖直向上且大小不变，不能反映立管张力的变化，得到的张力环位置的弯矩过大，立管上部的水平位移结果偏大，而立管垂向位移的运动范围偏小。

(2)由于忽略低压氮气和活塞重力的作用，传统的简化模型过高评估了张紧器的张力水平。如采用传统的简化模型进行模拟，立管底部的弯矩和立管的水平位移均偏小，而立管垂向位移相对向上偏移。

(3)本文建立的线性和非线性弹簧阻尼模型之间的差别主要体现在立管受到的张力和垂向位移上，而立管受到的弯矩和水平位移的差别取决于在具体张紧器结构参数和工况下二者模型之间的张力差别，当二者张力差别不大时，可以采用线性弹簧-阻尼模型进行模拟计算，而当二者张力差别较大时，需充分考虑张紧器张力非线性变化的特性。在极端载荷工况下，建议采用非线性弹簧-阻尼模型模拟张紧器。