析学情 定目标 让生成更精彩
——以“菱形”第一课时为例
■刘思武
一、教学目标及学情分析
在教授“菱形”第一课时前,首先要分析教学目标。教参上写的是平行四边形、矩形、菱形、正方形5个课时的教学目标,再翻阅《义务教育数学课程标准》关于“菱形”的目标:性质与判定。无论教参还是课标,给出的都是上位教学目标,作为一线的数学教师应该根据自己学生的实际情况制订下位目标,唯有适合自己学生的教学设计才是最好的。所以我仔细分析学情,制定了这样的教学目标:1.知道菱形的定义,并利用菱形的定义探究性质;2.应用菱形的性质解决简单的问题;3.知道菱形与平行四边形的内在联系。本节课的教学重难点又是什么?仔细分析本班学情,初二下学期的学生已经有了一些几何学习的经验,知道几何学习的一般路径:定义、性质、判定以及应用。我认为本节课的教学重难点是:利用菱形的定义探索菱形的性质。这就回到数学教学的根本——概念教学。
二、课堂生成
师:我们知道,任意三角形绕一边中点旋转180°,得到的三角形与原三角形构成平行四边形。等腰△ABC,AB=AC,将△ABC绕BC中点M旋转180°,旋转之后的三角形与原三角形构成了什么图形?
生(齐答):菱形!
师:同学们今天看到后面有老师听课,所以表现得很积极,谢谢你们!但请大家像平时一样不要齐答,举手回答问题。
生:……(抿嘴相视而笑)
教学思考:每节数学课首先应该是最真实的,而齐答让课堂看起来很热闹,但是容易掩盖一部分真实的东西。原生态的课堂才是我们应该追求的!所以在课堂上让学生举手起立回答或者坐在位置上回答,这样的课堂生成相对而言更真实一些。本节课是在平行四边形、矩形之后的学习内容,接着还会有正方形的学习,这四项学习内容应该是前后一致、一以贯之的,所以在选取导入情境时应该兼顾前后,所以以三角形的旋转引入应该是不错的选择。
师:请大家在方格本上(我要求学生从初一开始就使用细方格本记笔记,方便画图,节约时间)画一个等腰△ABC,底边BC水平放置,且为偶数个单位长度,取BC中点M,如图1所示,请画出将△ABC绕点M旋转180°之后的图形。
师生活动:学生画图,教师巡视,并展示优秀学生作品。大部分学生能画出如图2所示的图形,教师再用几何画板演示旋转的过程。

图1

图2
教学思考:有的教师认为没必要让学生在课堂上再画图,浪费时间。但根据本班学生的学习情况,我认为是有必要的。在几何学习的过程中,很多初中生感觉比较困难。如何学好几何?首先要从图形入手,如果学生有较强的画图、识图的能力,这对几何推理能力的提升有非常好的促进作用,所以在教学几何相关知识时,我常常板书完整的画图过程,学生跟着画图,虽然“吃力”,但是我却认为能“讨好”。
师:首先这个四边形一定是什么四边形?
生1:平行四边形。
生2:这是一个特殊的平行四边形!
师:特殊在哪里?
生3:因为△ABC是等腰三角形,所以AB=AC,即有一组邻边相等。
师:对,我们常说要“用好已知”!这样的平行四边形就是菱形。
给出菱形的概念(教师板书,学生记笔记):有一组邻边相等的平行四边形叫作菱形。记作:菱形ABCD。

师:你觉得下面要研究菱形的什么方面呢?
生4:性质。
师:菱形会具有什么性质呢?
追问:该从哪几个角度研究它的性质呢?
教学思考:考虑到一部分基础比较薄弱的学生对知识的掌握以及遗忘程度,我在巡视的过程中追加提示问:平行四边形、矩形是怎么研究的?
学生活动:请同学们从菱形的定义出发,完成下面的表格。
教学思考:基于学情进行教学设计,不能仅仅是一句口头禅,要落到实处。下面的表格,既给了学生一定的提示,也给学生指出菱形性质研究的方向。
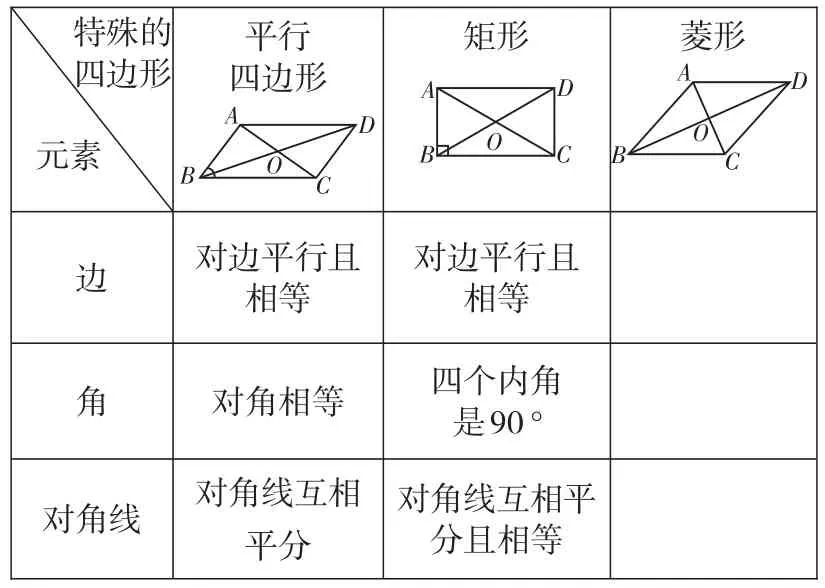
特殊的四边形元素平行四边形矩形菱形A D D A A D B O B C C B O C对边平行且相等边 角对角相等对角线互相平分对角线对边平行且相等四个内角是90°对角线互相平分且相等O
学生根据图形能猜出(类比出)菱形的性质。
总结:菱形具有平行四边形的一切性质,如中心对称,轴对称图形,两条对称轴。
特有性质:(1)菱形的四边相等;(2)对角线互相垂直。
(教师板书,学生记笔记。)
教学思考:因为多媒体的常态化使用,很多教师已经不习惯写板书了。板书是教师的一项基本功,也是整节课的思维痕迹的体现。在平时,我每节课都有板书,并用手机拍摄,同时要求学生尽量记录。教师板书时,一定要让学生有事可做,开始学生是嫌麻烦的,但是时间久了,他们习惯了记录板书,在复习时常会大呼痛快,因为笔记能够再次呈现课堂的生成过程,重难点都能够体现出来!
师生活动:证明你所发现的菱形的性质,将证明过程说给小组内的同学听,组内同学一起完善证明过程。教师巡视并给予指导,展示优秀和不完善的作品,一起优化。其中“对角线互相垂直”要作为重点内容讲解。教师要板书,学生要记录,追求一题多解。
教学思考:小组活动要适量,不能多,多了就是假热闹。在菱形性质的证明中,“对角线互相垂直”是重点,可以将很多知识贯穿在一起。同时教师要给学生展示的机会,要给予及时的评价,给他们一个慢思考的机会。
师:刚刚老师在巡视的过程中,发现有三位同学发现了菱形对角线平分一组对角,这是非常棒的,你们能证明它吗?
生5:全等或者等腰三角形的“三线合一”!
师:非常好!这个性质是一个真命题,但是不可以作为定理,如果你想利用它就得像生5一样把它证明出来!
例题:摆放两张宽度相同的矩形纸片,让重叠部分是一个四边形,仔细观察,它是什么四边形?证明你的结论。

教学思考:此处插入一项学生活动,用两张等宽的纸条进行重叠,一张透明一张不透明,我是让学生自己画出图形的(我始终认为几何教学中一定要让学生多画图)。对于例题的选择我也有过一些思考,本节课是在定义的基础上探究性质,所以性质是重点,教材的例题是利用菱形解决问题。但我还是觉得有必要对定义进行深入的了解,当然利用定义判断菱形对于学生是有一点挑战的,适当尝试一下又何妨?
师生活动:学生小组讨论,大部分学生能说出四边形ABCD为平行四边形,学生先书写出判断平行四边形的证明过程。
追问:在解题时,我们常说“用好已知”,矩形的宽度如何体现出来呢?
教学思考:学生不容易证明出这是一个菱形,但是通过这个追问给予他们一定的提示,再进行小组讨论,学生会在上一节课的基础上想到作高,高出来了之后,条件就呈显性的了。课堂上对一题整理一种方法,课后感兴趣的学生自行整理其他方法。当然本节课的重点还是加强对性质的应用,所以出示下面的变式训练题。
变式:连接对角线AC、BD交于O点。
(1)若AC=12,BD=16,求四边形ABCD的周长。
(2)若∠ABC=60°,AB=4,求BD的长和四边形ABCD的面积。
师生活动:学生独立完成相应的图形,标注条件,自己尝试写出证明过程,小组内部交流完善,教师巡视并给予适当指导。
教学思考:在平时的教学中,由于课时的限制、进度的要求,教师不愿意让学生多表达,因为“教学任务”要完成,学生说多了就会“浪费”时间,教学任务完成不了。然而“有舍才有得”,有时候学生很愿意表达自己的想法,只要给他们机会,学生会让课堂有更精彩的生成。教师要充分调动学生的积极性,在评价时可以慢半拍,一旦学生尝到了“甜头”,就会愿意积极思考、表达想法,学生的主体地位在课堂上就会慢慢凸显。课堂教学是为了学生,同时课堂的生成也来源于学生的思考。在平时的课堂中,将目标细化,设计合理,把发言权交给学生,教师适时指导、积极评价,就一定会有意想不到的精彩生成,作为数学教师就增添了继续前行的动力,也是我们的乐趣所在!让每一位数学人都能够热爱数学教学,感受数学思维的熏陶,让每一个学生都能热爱数学学习,受益终生!

